Развертка поверхности неправильной пирамиды в начертательной геометрии с примером

Развертка поверхности неправильной пирамиды:

Развертка поверхности неправильной пирамиды будет состоять из неправильных треугольников боковой поверхности и неправильного треугольника, лежащего в основании, совмещенных в одну плоскость, причем их взаимное расположение на развертке должно соответствовать взаимному расположению на ортогональных проекциях. Так как у неправильной пирамиды стороны основания разные и ребра боковой поверхности не равны между собой, сначала находим натуральную величину всех боковых ребер (рис. 5.12). Для этого используем один из способов определения натуральной величины отрезка прямой общего положения. В данном случае использован способ вращения. Боковые ребра вращаем вокруг оси, проведенной через вершину пирамиды S перпендикулярно плоскости Н. На чертеже фронтальная проекция оси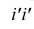

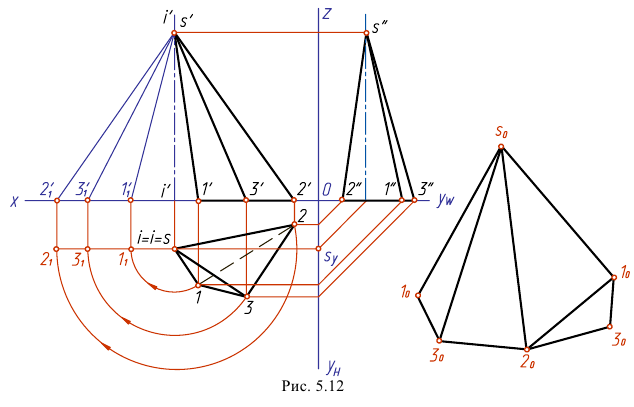
Стороны основания 12, 23 и 13 спроецировались в натуральную величину на горизонтальную плоскость проекций. Зная натуральные величины всех элементов пирамиды, приступаем к построению развертки ее поверхности. При построении развертки боковой поверхности используем способ построения треугольников по трем заданным сторо­нам. Построение можно начать с любой грани боковой поверхности, например с грани 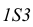(рис. 5.12). Сначала на свободном месте чертежа проводим произвольную прямую и на ней откладываем натуральную величину стороны основания 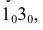взятую с горизонтальной проекции.

Затем из точки 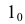радиусом, равным натуральной величине ребра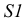 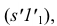а из точки 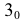радиусом, равным натуральной величине ребра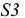 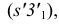делаем засечки до пересечения в точке 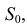которая будет вершиной развертки боковой поверхности пирамиды. Далее строим боковую грань 3S2. Для этого на фронтальной проекции циркулем измеряем на­туральную величину ребра 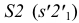и на развертке этим радиусом из вершины 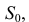а из точки 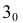радиусом 32, взятым с горизонтальной проекции, делаем засечки до пересечения в точке 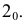Соединив точку 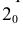пря­мой линией с вершиной 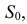получим вторую грань 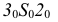боковой поверхности пирамиды. Третья грань и основание сроятся тем же способом.