
Разложение силы на две составляющие в теоретической механике
Разложение силы на две составляющие:
Решение многих практических задач по статике сводится к разложению силы на две составляющие. Подобные задачи решаются либо по правилу параллелограмма, либо по правилу треугольника и, в зависимости от исходных данных, приводятся к одному из четырех типов.
Общая методика решения приведенных ниже задач сводится к следующему:
- Выбираем метод решения — графический или графо-аналитический.
- Выбираем правило, по которому будем решать задачу, т. е. либо правило параллелограмма, либо правило треугольника.
- Если выбран графический метод, то далее выбираем масштаб построения, строим параллелограмм или треугольник (в соответствии с выбранным правилом) и, наконец, измеряем стороны получившейся фигуры, находим модули соответствующих сил, а измерив углы, найдем их направления.
- Если выбран графо-аналитический метод, то в зависимости от избранного правила строим параллелограмм или треугольник, соблюдая приблизительные соотношения размеров длин и углов, а затем, в зависимости от исходных данных, используем геометрические или тригонометрические соотношения.
Задача №1
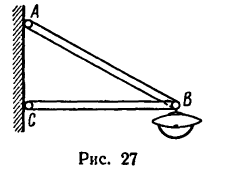
Фонарь весом 80 н подвешен на кронштейне АВС, укрепленном на вертикальной стене (рис. 27). Определить усилия, возникшие в горизонтальном стержне СВ и наклонной тяге АВ после подвески фонаря, если СВ = 1 ли /AB = 1,2 л. Соединения в точках А, В и С кронштейна - шарнирные.
Решение 1—графическим методом по правилу параллелограмма.
1. Если избран графический метод решения, то прежде всего необходимо в масштабе построить кронштейн АВС. Выполнение чертежа кронштейна сводится, как это следует из формы и размеров, заданных в условии задачи, к построению прямоугольного треугольника по двум заданным сторонам.
2. Построим кронштейн в масштабе «1 м в 44 мм». Обозначив масштаб чертежа 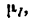
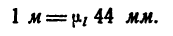
Отсюда масштаб построения кронштейна
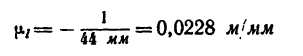
3. Из произвольной точки С (рис. 28) проводим горизонтальную и вертикальную линии. На горизонтальной линии отложим
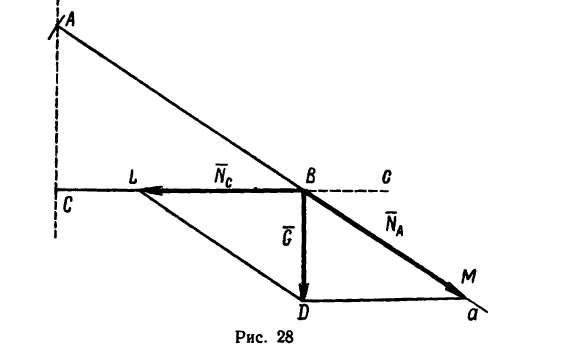
отрезок ВС = 44 мм, который в выбранном масштабе и изобразит горизонтальный стержень кронштейна 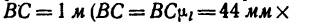
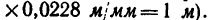
Длина отрезка АВ, который изобразит тягу АВ, определяется из равенства
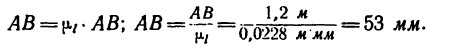
Найденную длину АВ = 53 мм отложим при помощи циркуля из точки В так, чтобы получить точку А на вертикали, проведенной ранее из точки С. Построенный треугольник АВС изображает данный в условии задачи кронштейн.
4. Строим параллелограмм сил, действующих на точку В кронштейна.
Вес фонаря G = 80 н, действующий на кронштейн вертикально вниз, изобразим отрезком BD=20 мм. Значит масштаб построения
для сил
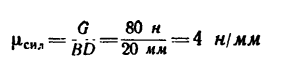
(4 н в 1 мм).
Благодаря тому что в точках А, В и С кронштейна соединения шарнирные, стержни, находясь под действием веса фонаря, либо растягиваются, либо сжимаются. Иными словами, искомые усилия действуют вдоль стержней. Значит направления сил известны (1-й тип задачи на разложения силы по правилу параллелограмма).
Изобразим направление действия искомых сил линиями Аа и Сс, пересекающимися в точке В — точке приложения к кронштейну веса фонаря.
Из точки D (конца вектора 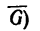 проводим прямые DM || Сс и
проводим прямые DM || Сс и  В получившемся параллелограмме BMDL стороны ВМ и BL изображают силы
В получившемся параллелограмме BMDL стороны ВМ и BL изображают силы 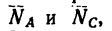 действующие соответственно на тягу АВ и стержень ВС.
действующие соответственно на тягу АВ и стержень ВС.
5. При помощи масштабной линейки измерим отрезки ВМ и BL:
ВМ=36 мм и BL—30 мм.
Следовательно,
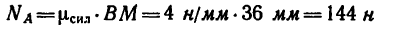
и
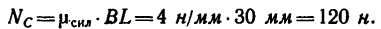
Как видно из получившегося на рис. 28 построения, тяга АВ кронштейна растягивается силой, равной 144 н, а стержень ВС сжимается силой 120 н.
Решение 2—графо-аналитическим методом по правилу параллелограмма с использованием геометрических соотношений.
1. Используя рис. 27, на котором изображен кронштейн, строим параллелограмм сил. Через произвольную точку а (рис. 29) проводим прямые  параллельные соответственно тяге АВ и стержню СВ (рис. 27).
параллельные соответственно тяге АВ и стержню СВ (рис. 27).
Из той же точки а откладываем вертикально вниз отрезок ab, который изображает силу  Из точки b проводим прямые
Из точки b проводим прямые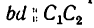 и
и 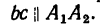 В получившемся параллелограмме adbc стороны ad и ас изображают соответственно искомые усилия
В получившемся параллелограмме adbc стороны ad и ас изображают соответственно искомые усилия 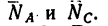
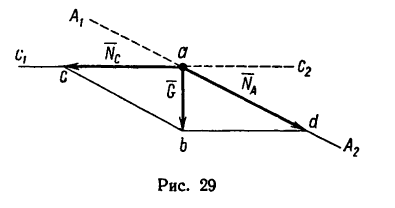
2. Теперь имеются две геометрические фигуры — треугольник АВС (см. рис. 27), изображающий заданный кронштейн, и силовой параллелограмм (см. рис. 29).
Геометрически 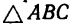 (см. рис. 27) и
(см. рис. 27) и 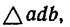 или, что все равно,
или, что все равно, 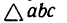 (см. рис. 29), подобны между собой.
(см. рис. 29), подобны между собой.
Используя свойство подобных треугольников (замечаем, что db = ac—Nc), получаем
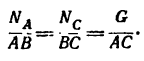
3. Решая получившиеся пропорции, находим
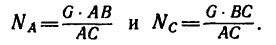
Неизвестную в кронштейне длину АС найдем по теореме Пнфагора (из условия задачи ясно, что угол АСВ - прямой)
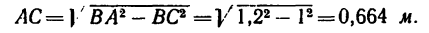
Подставляя в выражения для 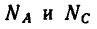 исходные данные, получаем
исходные данные, получаем
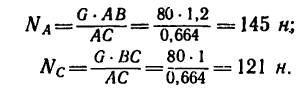
Таким образом, результат практически тот же, что и при графическом решении. Некоторое расхождение объясняется меньшей точностью графического решения.
Как уже известно, графо-аналитическое решение задачи 22-6 основано на подобии двух треугольников: кронштейна, имеющего вид треугольника, и силового треугольника. Но возможен случай, когда на чертеже нагруженного устройства или конструкции не будет треугольника, подобного силовому. Тогда для решения задачи целесообразно применить графо-аналитический метод с использованием тригонометрических соотношений.
Рассмотрим такую задачу.
Задача №2
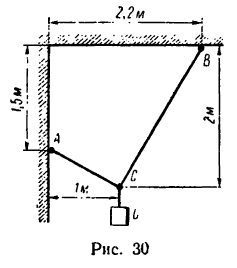
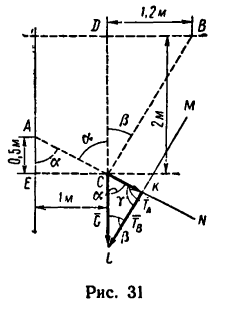
При помощи двух нерастяжимых нитей АС и ВС удерживается груз, вес которого 12 кГ. Положение нитей и груза показано на рис. 30. Определить натяжение нитей.
Решение 1 - графо-аналитическим методом по правилу треугольника с использованием тригонометрии.
1. Так же, как и в предыдущей задаче, необходимо силу G=12 кГ разложить на две составляющие, линии действия которых совпадают с направлениями линий АС и ВС.
2. Изобразим силу 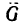 отрезком
отрезком 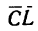 (рис. 31). Затем проведем из точки С прямую CN, продолжив АС, а из точки L — прямую LM параллельно положению нити ВС. Получим силовой треугольник CKL, в котором стороны СК и K.L изображают искомые силы натяжения нитей АС и ВС.
(рис. 31). Затем проведем из точки С прямую CN, продолжив АС, а из точки L — прямую LM параллельно положению нити ВС. Получим силовой треугольник CKL, в котором стороны СК и K.L изображают искомые силы натяжения нитей АС и ВС.
3. Если в треугольнике CKL известны углы а,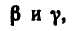 то задачу легко решить по теореме синусов:
то задачу легко решить по теореме синусов: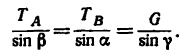
4. Из построения силового треугольника следует, что 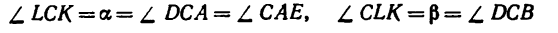
(для наглядности положение нитей относительно вектора G показано на рис. 31 штриховой линией). А так как треугольники  АСЕ и
АСЕ и  BCD- прямоугольные, то из
BCD- прямоугольные, то из ACE
ACE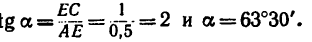
Из 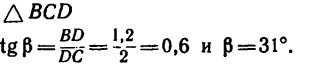
Угол у легко найдем как дополнение к 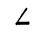 180°:
180°:
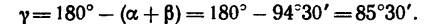
5. И теперь, зная углы а,  из уравнения (1)
из уравнения (1)
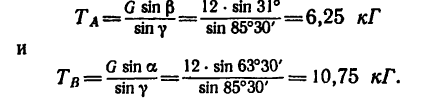
Таким образом, нить С А растягивается усилием, равным 6,25 кГ, а нить СВ - усилием 10,75 кГ.
Если эти усилия выразить в единицах СИ, то
и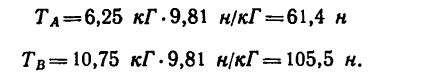
Задачу просто решить графическим методом. Для этого нужно начертить в масштабе расположение нитей и, выбрав масштаб для сил (например, 0,2 кГ/мм), построить на векторе G силовой треугольник и, измерив его стороны, найти (графическое решение рекомендуется выполнить самостоятельно).
(графическое решение рекомендуется выполнить самостоятельно).
Графо-аналитический метод с использованием свойств подобных треугольников целесообразно применять к решению таких задач в том случае, если в схеме конструкции или устройства имеется треугольник, подобный силовому.
Если же в схеме конструкции нет треугольника, подобного силовому, то решение графо-аналитическим методом целесообразнее производить с использованием тригонометрических свойств, потому что при наличии линейных размеров необходимые для решения задачи значения углов, как правило, найти очень просто.
Необходимо отметить, что в задачах, подобных 22-6 и 23-6, усилия, вызываемые нагрузкой в стержнях кронштейнов или нитях устройств, удерживающих груз, не зависят от длины этих нитей или стержней.
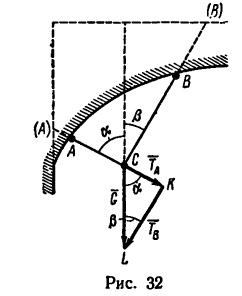
Допустим, что груз (задача 23-6) удерживается нитями, прикрепленными не к вертикальной стенке и горизонтальному потолку, как на рис, 30, а к двум точкам криволинейной (сводчатой) поверхности (рис. 32). Но если при этом углы аи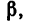 , образуемые нитями СВ и С А с вертикалью, остаются такими же, как и на рис. 30, то усилия
, образуемые нитями СВ и С А с вертикалью, остаются такими же, как и на рис. 30, то усилия 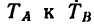 не изменяются, хотя сами нити в данном случае становятся короче.
не изменяются, хотя сами нити в данном случае становятся короче.
Задача №3
Груз весом G= 12 кГ удерживается при помощи двух нитей, которые образуют с вертикалью (линией действия веса G) углы а=65° и 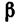 = 90“. Определить усилия, растягивающие нити.
= 90“. Определить усилия, растягивающие нити.
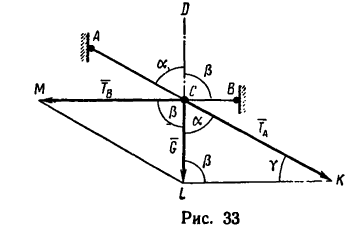
Решение—графо-аналитическим методом по правилу параллелограмма.
1. Исходя из условия задачи, построим чертеж (рис. 33). Из точки С проводим вертикальный отрезок CL, изображающий вектор 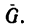 Отложив (приблизительно) от вертикали CD влево угол а, а вправо - угол
Отложив (приблизительно) от вертикали CD влево угол а, а вправо - угол 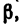 проведем нити С А и СВ (длины нитей не влияют на величину усилий, поэтому точки А и В выбираем произвольно).
проведем нити С А и СВ (длины нитей не влияют на величину усилий, поэтому точки А и В выбираем произвольно).
2. Вектор 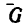 по правилу параллелограмма разложим на две составляющие
по правилу параллелограмма разложим на две составляющие 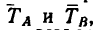 направленные вдоль нитей, т. е. построим параллелограмм CKLM
направленные вдоль нитей, т. е. построим параллелограмм CKLM
3. На основе построения параллелограмма CKLM очень просто определяются его углы:
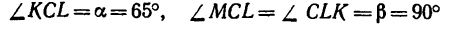
и, следовательно,
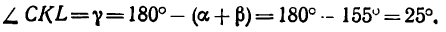
4. Так как силовой параллелограмм делится на два прямоугольных треугольника, то легко найти оба усилия:
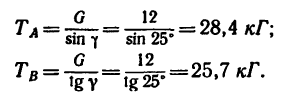
единицах СИ усилия равны:
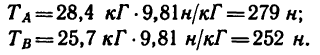
Задачи 6 относятся к первому типу задач на разложение силы по правилу параллелограмма или треугольника.
Рассмотрим теперь по одной задаче второго (задача 25-6), третьего (задача 26-6) и четвертого (задача 27-6) типов.
Задача №4
Груз массой 200 кг необходимо подвесить на кронштейне, у которого один из стержней горизонтальный и в нем должно возникнуть сжимающее усилие не более 1,5 кн.
Как нужно расположить второй стержень, чтобы в нем возникло растягивающее усилие? Определить величину этого усилия.
Эта задача аналогична задаче 8-2, которая решена графическим методом, поэтому графическое решение здесь не приводим.
Решение —графо-аналитическим методом по правилу треугольника.
1. Изобразим (рис. 34, а) стержень АВ в горизонтальном положении, т. е. в том, какое он должен занимать по условию, и допустим, что к концу В стержня приложена нагрузка 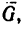 равная весу груза, т. е.
равная весу груза, т. е.
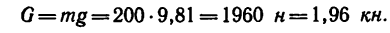
Известно, что этот стержень должен испытывать сжимающее усилие 1,5 кн. Поэтому сила, приложенная к стержню в точке В, будет направлена от В к А. Обозначим эту силу 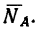
Расположение стержня ВС кронштейна неизвестно и поэтому он условно показан штриховой линией.
2. Строим силовой треугольник (рис. 34, б). Из произвольной точки D отложим вертикальный отрезок DE, изображающий вес груза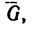 и горизонтальный отрезок DF, изображающий силу
и горизонтальный отрезок DF, изображающий силу 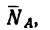 сжимающую стержень АВ, т. е. известное слагаемое ректора G.
сжимающую стержень АВ, т. е. известное слагаемое ректора G.
Для того чтобы найти второе слагаемое вектора 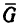 — вектор
— вектор 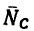 (усилие в стержне ВС), необходимо из вектора
(усилие в стержне ВС), необходимо из вектора 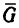 вычесть вектор
вычесть вектор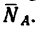
Чтобы выполнить это действие по правилу треугольника, соединим точки F и Е. Сторона FE получившегося треугольника изображает искомое усилие  (правило вычитания векторов показано на рис. 3).
(правило вычитания векторов показано на рис. 3).
3. Треугольник DEF прямоугольный, поэтому
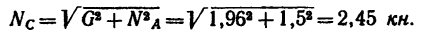
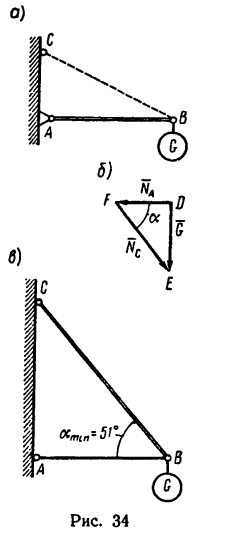
Если мысленно в точку В кронштейна перенести силу 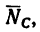 то ее направление определит положение стержня ВС относительно АВ.
то ее направление определит положение стержня ВС относительно АВ.
Угол АВС (рис. 34, в) между стержнями должен быть равен углу между линиями действия сил 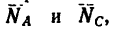 т. е. углу DFE=a:
т. е. углу DFE=a:
и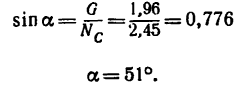
Таким образом, если в кронштейне стержень ВС расположить к горизонтальному стержню В А под углом а=51°, то груз весом G = l,96 кн, действующий на точку В кронштейна, вызовет в стержне В А сжимающее усилие 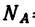 = 1,5 кн, а в стержне ВС —растягивающее усилие
= 1,5 кн, а в стержне ВС —растягивающее усилие 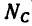 = 2,45 кн.
= 2,45 кн.
Если при изготовлении кронштейна увеличить угол a(a>51°), то уменьшится нагрузка на оба стержня, причем при вертикальном положении стержня ВС (а = 90°) усилие 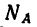 в горизонтальном стержне станет равным нулю, а 7VC=G= 1,96 кн.
в горизонтальном стержне станет равным нулю, а 7VC=G= 1,96 кн.
Если же при изготовлении кронштейна угол а уменьшить (а < 51°), то усилия в обоих стержнях увеличатся.
В этом легко можно убедиться, построив на заданном векторе G силовые треугольники, углы которых а>51° или а<51°.
Задача №5
Между высокими стенами необходимо временно подвесить некоторый груз весом 140 кГ на одинаковом расстоянии по 1 мот стен и на высоте 1 м от горизонтального пола. Имеются два куска каната по несколько метров длины каждый. Один из канатов с учетом безопасности подвески можно нагрузить усилием не более 70 кн, а второй — усилием не более 100 кн.
На какой высоте над полом необходимо укрепить концы канатов, чтобы после подвески к ним груза в заданном положении усилия в кан.атах не превышали допускаемых 70 и 100 кн?
Решение 1 — графическим методом по правилу параллелограмма.
1. Выбираем масштаб построения так, что длина 1 м изображается на чертеже отрезком, равным 12,5 мм (1 м в 12,5 мм):
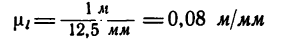
и строим две вертикальные стены и горизонтальный пол (рис. 35).
В выбранном масштабе расстояние I — 2 м между стенами на чертеже изобразим отрезком, равным
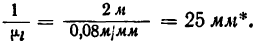
На расстоянии 1 м от пола и по 1 м от стен отмечаем точку А, в которой должен быть подвешен груз.
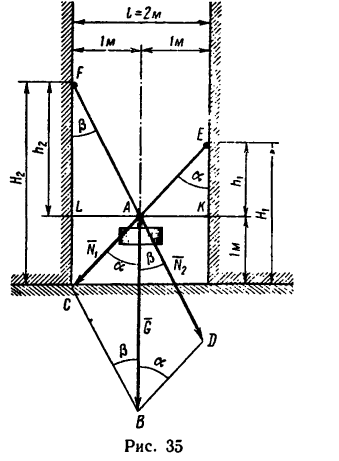
1. Выбираем масштаб сил  =4 кн/мм (4 /сн в 1 мм длины). Значит грузв G=140 кн изобразится отрезком
=4 кн/мм (4 /сн в 1 мм длины). Значит грузв G=140 кн изобразится отрезком
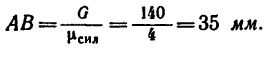
Отложим этот отрезок из точки А на чертеже.
По условию задачи, усилие в канатах не должно быть больше 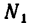 =
=
= 70 кн и 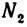 =100 кн. Эти усилия в выбранном масштабе изобразятся отрезками
=100 кн. Эти усилия в выбранном масштабе изобразятся отрезками
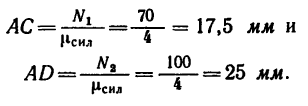
Сделав при помощи циркуля засечки радиусами, равными этим длинам, сначала из точки А, а затем из точки В получим параллелограмм ACBD.
3. Усилия  должны действовать вдоль канатов, поэтому, продлив отрезок СА до пересечения с правой стеной, получим на ней точку Е—место закрепления одного каната и, продлив отрезок DA, получим на левой стене точку F—место закрепления второго каната.
должны действовать вдоль канатов, поэтому, продлив отрезок СА до пересечения с правой стеной, получим на ней точку Е—место закрепления одного каната и, продлив отрезок DA, получим на левой стене точку F—место закрепления второго каната.
4. Измерив на чертеже расстояние от точки Е до линии пола, получим 25 мм, значит точка закрепления первого каната должна находиться от пола на расстоянии, не меньшем
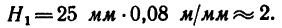
Измерив расстояние от точки F до линии пола, получим 36 мм. Значит точка закрепления второго каната должна находиться от пола на расстоянии, не меньшем
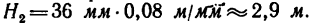
Для большей безопасности подвески, если позволяют длины кусков канатов, обе точки их закрепления можно поднять выше. Усилия в канатах при этом уменьшатся.
Решение 2 — графо-аналитическим методом по правилу параллелограмма.
* Описываемое в тексте построение рекомендуется воспроизвести на листе бумаги, но в ином масштабе, например 0,04 м,мм или 0,02 м/мм.
1. Для графо-аналитического решения нужно также выполнить чертеж без соблюдения точного масштаба. Воспользуемся рис. 35, на котором ясно видно, что искомые расстояния можно получить как суммы
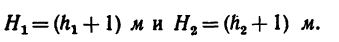
Расстояния 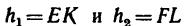 можно найти из прямоугольных треугольников АКE и ALF, если предварительно определим в них углы а и
можно найти из прямоугольных треугольников АКE и ALF, если предварительно определим в них углы а и 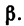
Углы, равные аи 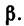 содержатся в параллелограмме ACBD:
содержатся в параллелограмме ACBD:
и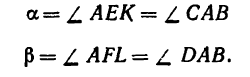
2. Из 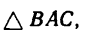 в котором стороны изображают данные силы
в котором стороны изображают данные силы 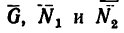 (так как
(так как 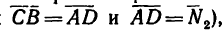 найдем угол а, применив теорему косинусов:
найдем угол а, применив теорему косинусов:
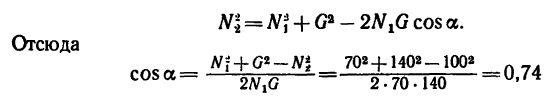 .
.
Так как l.  то угол
то угол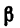 p можно определить из того же
p можно определить из того же  применив к 'нему теорему синусов:
применив к 'нему теорему синусов:
Отсюда и, следовательно,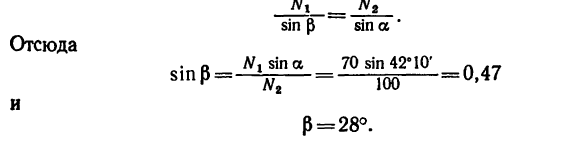
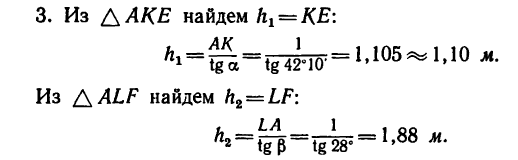
4. Таким образом, искомые расстояния от мест закрепления канатов до пола равны:
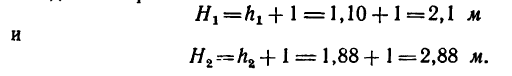
Сравнив результаты, полученные в решении 2, с результатами графического решения, увидим, что практически они совпадают.
Задача №6
На конце В стержня АВ, длина которого АВ = 1, шарнирно прикрепленного в точке А к вертикальной стене, необходимо подвесить груз весом G =6 кн, причем стержень АВ должен образовывать со стеной угол 45° (рис. 36, а).
На каком расстоянии Н от точки А необходимо прикрепить трос СВ, удерживающий стержень в заданном положении, если трос может быть нагружен усилием не более 4,5 кн? Определить также усилие, возникшее в стержне АВ после подвески к нему груза.
Решение — графо-аналитическим методом по правилу параллелограмма (графическим методом рекомендуется решить задачу самостоятельно).
1. Из произвольной точки а в произвольном масштабе проведем отрезок ab, который Изобразит вектор G - вес груза (рис. 36,6).
Так как стержень АВ должен занимать положение под углом 45° к вертикальной стенке, то усилие S в этом стержне будет направлено под углом 45° к направлению 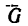
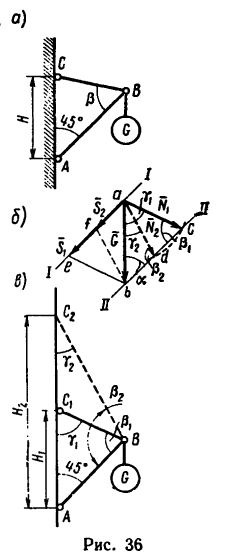
Проведем из точек а и b вектора  параллельные прямые под углом а=45°к линии действия вектора
параллельные прямые под углом а=45°к линии действия вектора 
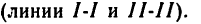
Если теперь из точки а отложить вектор, численно равный усилию N = 4,5 кн, максимально допустимому в тросе ВС (см. рис. 36,а), то увидим, что этот отрезок пересечет линию 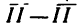 в двух точках - в точках cud. Проделав ту же операцию из точки Ь, получим два параллелограмма: первый
в двух точках - в точках cud. Проделав ту же операцию из точки Ь, получим два параллелограмма: первый 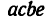 и второй
и второй 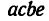
Это значит, что задача допускает бесчисленное множество решений*. При одном и том же направлении усилия 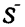 в стержне АВ трос может быть направлен к стержню под углом
в стержне АВ трос может быть направлен к стержню под углом 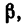 но не менее
но не менее 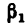 и не более
и не более 
2. Найдем предельные значения углов 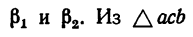 или
или 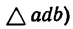 по теореме синусов
по теореме синусов
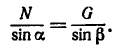
* В предельном случае, если уменьшим заданное допускаемое усилие в тросе, задача может иметь одно решение (дуга cd проведенная изо, касается линии ll-11). При дальнейшем уменьшении допускаемого усилия в тросе задача практически неосуществима.
Отсюда
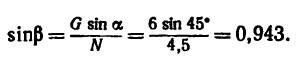
Этому значению соответствуют два значения угла 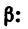
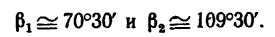
Следовательно, трос ВС можно закрепить в точке 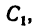 направив его под углом
направив его под углом 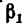 к стержню АВ, или в точке
к стержню АВ, или в точке 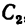 , направив его к стержню под углом
, направив его к стержню под углом 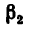 (рис. 36, в), а также в любой другой точке между
(рис. 36, в), а также в любой другой точке между 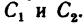
3. Если принять решение 1, то из 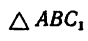 (см. рис. 36, в)
(см. рис. 36, в)
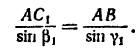
Отсюда, зная, что АВ = l и найдя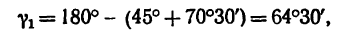
получим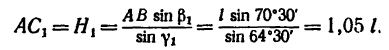
При этом выборе решения усилие S в стержне АВ равно ( abc; см. рис. 36, б)
abc; см. рис. 36, б)
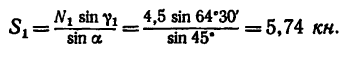
4. Если принять решение 2, то из 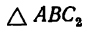 (см. рис. 36, в)
(см. рис. 36, в)
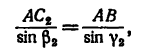
где
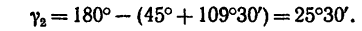
Поэтому
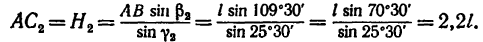
При этом решении усилие 5 в стержне АВ равно (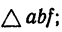 см. рис. 36, б)
см. рис. 36, б)
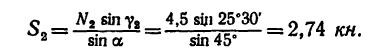
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |