Равновесие вала в теоретической механике

Равновесие вала:

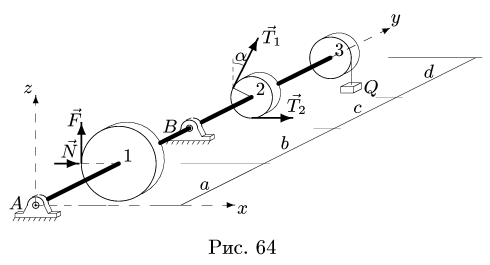
Постановка Задачи. Горизонтальный вал может вращаться в цилиндрических шарнирах. К одному шкиву вала приложено нормальное давление и касательная сила сопротивления, пропорциональная давлению. На шкивы вала действуют известные нагрузки. Найти силу давления и реакции шарниров при условии равновесия вала.

План решения:

1. Действие каждой из опор заменяем двумя взаимно перпендикулярными реакциями, лежащими в плоскости, перпендикулярной валу.

2. Для определения силы давления составляем уравнение моментов относительно оси вала. Момент силы натяжения ремня, нити и т.п. (наклонной или нет) вычисляем как произведение величины силы на соответствующий радиус со знаком, соответствующим направлению вращения вокруг вала. Уравнение содержит одну неизвестную, которую легко найти.

3. Определяем вертикальные реакции опор вала. Для этого составляем два уравнения моментов относительно осей, совпадающих с линиями действия горизонтальных реакций шарниров. Решаем эти уравнения.

4. Проверяем найденные реакции, составляя уравнение равновесия в проекции на вертикаль.

5. Определяем горизонтальные реакции опор вала. Для этого составляем два уравнения моментов относительно осей, совпадающих с линиями действия вертикальных реакций шарниров.

6. Проверяем горизонтальные реакции, составляя уравнение равновесия в проекции на ось вдоль линии действия горизонтальных реакций.

Задача:

Горизонтальный вал весом G = 15 Н может вращаться в цилиндрических шарнирах А и В (рис. 64). К шкиву 1 приложено нормальное давление N и касательная сила сопротивления F = 0.1 N.

Решение

1. Действие цилиндрических опор А и В заменим реакциями 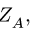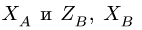(рис. 65). Вес вата 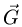приложим в центре. Вес груза изобразим вектором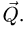

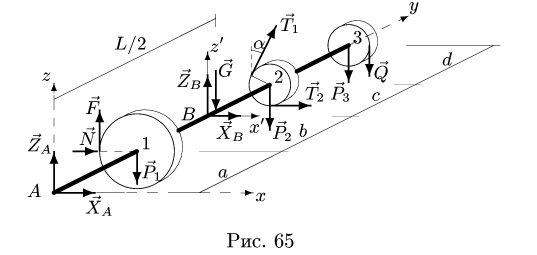
2. Для определения силы давления составляем уравнение моментов относительно оси вата:

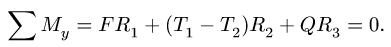
Уравнение содержит одну неизвестную F. Линии действия остальных сил пересекают ось 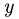и их моменты относительно оси вала равны нулю.

Из полученного уравнения находим

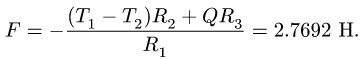
По условию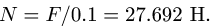

3. Определяем вертикальные реакции шарнирных опор вала. Для этого составляем два уравнения моментов относительно горизонтальных осей, проходящих через шарниры А а В. Рассматриваем для удобства проекцию всех сил на плоскость 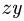(рис. 66). Таким образом вычисление моментов относительно осей сводим к плоской задаче вычисления моментов относительно точек А и В.

Знаки моментов сил определяем как в задачах плоской статики: момент силы, вращающей тело вокруг моментной точки против часовой стрелки считается положительным, по часовой стрелке — отрицательным. Моменты сил, перпендикулярных плоскости 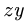(и поэтому не изображенных на рис. 66), относительно любой ее точки равны нулю.

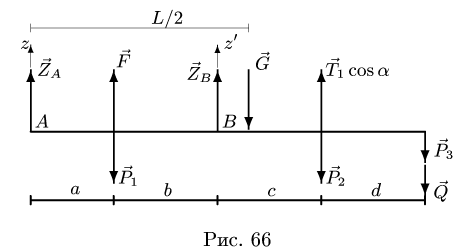
Решая уравнения

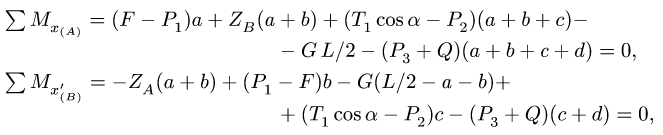
находим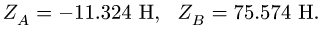

4. Проверяем правильность нахождения вертикальных реакций, составляя уравнение равновесия в проекции на ось 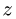(рис. 66):

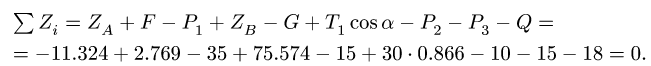
5. Определяем горизонтальные реакции опор вата. Для этого составляем два уравнения моментов относительно осей, совпадающих с линиями действия вертикальных реакций шарниров. Рассматриваем горизонтальную проекцию силовой схемы (рис. 67):

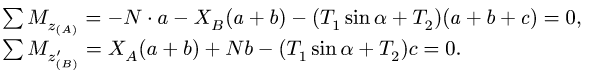
Решая уравнения, находим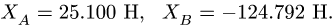

6. Проверяем правильность нахождения горизонтальных реакций, составляя уравнение равновесия в проекции на ось х вдоль линии действия горизонтальных реакции:

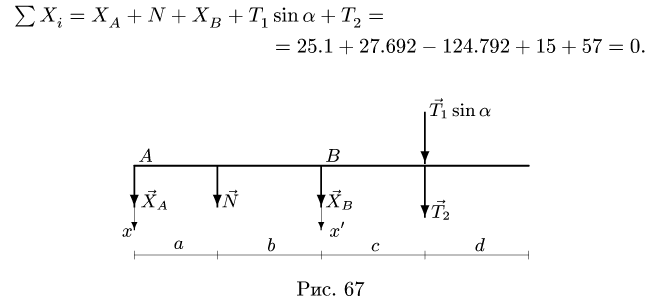
Результаты расчетов в 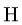заносим в таблицу: