
Равновесие тяжелой рамы в теоретической механике
Равновесие тяжелой рамы:
ПОСТАНОВКА ЗАДАЧИ. Тяжелая однородная рама расположена в вертикальной плоскости и опирается на неподвижный шарнир и наклонный невесомый стержень. К раме приложены внешние сосредоточенные силы и моменты. Учитывая погонный вес рамы, найти реакции опор.
План решения:
1.Согласно аксиоме о связях, освобождаем раму от связей. Действие опор заменяем их реакциями. Выбираем систему координат. В неподвижном шарнире имеются две неизвестные составляющие реакции (горизонтальная и вертикальная), а в невесомом опорном стержне — одна неизвестная реакция, направленная вдоль стержня. Все наклонные силы раскладываем на составляющие вдоль осей координат.
2. К центру каждого участка рамы прикладываем его вес, вычисленный по формуле 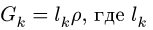
3. Составляем уравнение моментов всех сил, действующих на раму, относительно неподвижного шарнира. Определяем из этого уравнения реакцию опорного стержня.
4.Составляем уравнения проекций всех сил на оси х и у. Из этих уравнений определяем составляющие реакции неподвижного шарнира (горизонтальную и вертикальную).
5. Выполняем проверку решения, составляя уравнение моментов относительно какой-либо точки, не лежащей на линиях действия искомых реакций.
Задача:
Тяжелая однородная рама расположена в вертикальной плоскости и опирается на неподвижный шарнир А и наклонный невесомый стержень Н. К раме приложены внешние сосредоточенные силы 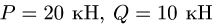 и момент
и момент 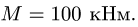 Дано:
Дано: 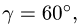
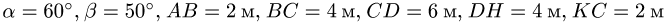 (рис.20).Учитывая погонный вес рамы
(рис.20).Учитывая погонный вес рамы 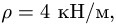 найти реакции опор.
найти реакции опор.
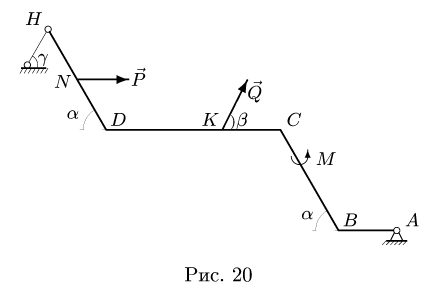
Решение
1.Освобождаем раму от связей. Действие опор заменяем их реакциями (рис. 21). Выбираем систему координат с началом в точке А. В неподвижном шарнире А реакция 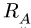 имеет две неизвестные компоненты
имеет две неизвестные компоненты 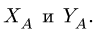 Невесомый опорный стержень в шарнире Н заменяем на его реакцию, направленную по стержню (т.е. под углом
Невесомый опорный стержень в шарнире Н заменяем на его реакцию, направленную по стержню (т.е. под углом 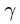 к горизонту).
к горизонту).
2.К центру каждого участка рамы (всего четыре прямолинейных участка) прикладываем его вес, вычисленный по формуле 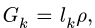 где-
где-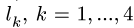 -длины отрезков рамы АВ, ВС, CD и DH,
-длины отрезков рамы АВ, ВС, CD и DH, 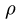 — погонный вес рамы.
— погонный вес рамы.
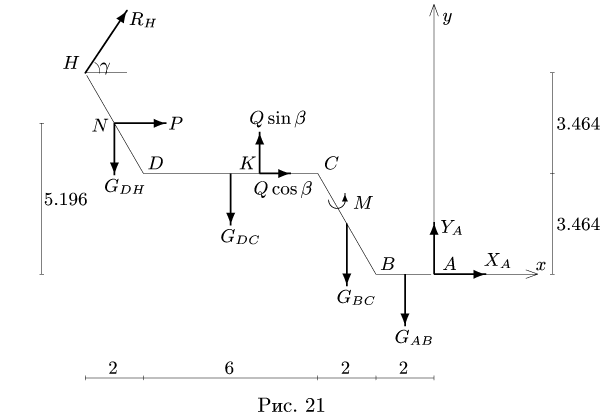
3. Составляем уравнение моментов относительно шарнира А, выделяя в нем для удобства счета отдельные слагаемые:
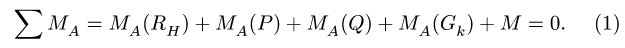
Момент 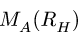 реакции опоры
реакции опоры
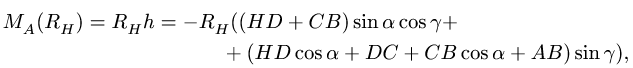
где h — плечо реакции 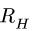 взятое со знаком момента.
взятое со знаком момента.
Моменты сил Р и Q и момент 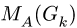 сил тяжести участков:
сил тяжести участков:
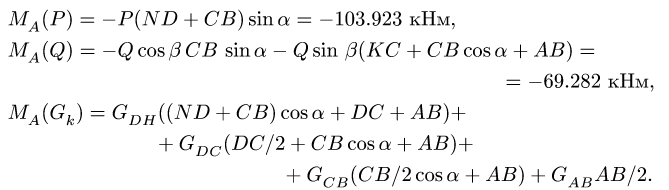
Вычисляя величины сил тяжести участков
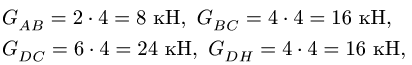
получаем 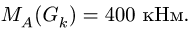
В итоге уравнение моментов (1) принимает вид
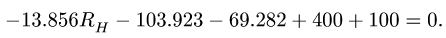
Отсюда находим реакцию стержня
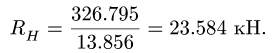
4. Реакции 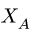 и
и 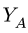 определяем из уравнений проекций:
определяем из уравнений проекций:
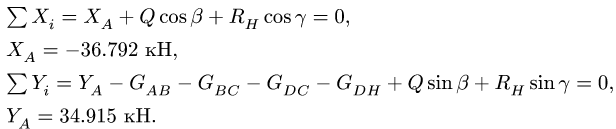
Ответы заносим в таблицу. Моменты — в кНм, силы — в кН.
5. Проверка. Составляем сумму моментов всех сил, действующих на раму, включая найденные реакции опор, относительно произвольной точки, например, К. Этот выбор оправдывается тем, что в уравнение моментов войдут все найденные реакции, а известная сила Q не войдет (ее проверять не требуется), и уравнение будет на два слагаемых короче
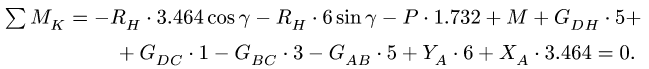
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |