Равновесие системы, состоящей из нескольких тел в теоретической механике

Равновесие системы, состоящей из нескольких тел:

До сих пор мы рассматривали равновесие одной материальной точки или одного твердого тела, находящихся под действием сил. При этом мы видели, что для одной точки можно составить два уравнения равновесия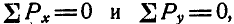

На практике же часто приходится иметь дело с системами, состоящими из нескольких материальных точек или твердых тел, соединенных между собой связями. Примерами таких систем могут служить машины, составленные из отдельных деталей, соединенных определенным образом между собой, сооружения, состоящие из отдельных блоков и пр.

На каждое из таких находящихся в равновесии тел действуют силы, часть которых представляет собой действие остальных тел системы на рассматриваемое и подлежит определению.

Так как при этом силы, действующие на каждое тело, вообще говоря, не пересекаются в одной точке, то для определения реакций связей в местах соприкасания тел с другими телами системы и связями можно для каждого из тел, входящих в систему, составить 3 уравнения равновесия, а для системы 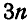уравнений. Если система, - находящаяся в равновесии, состоит из 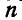материальных точек, то число таких уравнений равновесия будет .

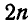Может оказаться при этом, что число неизвестных, подлежащих определению, превысит общее число уравнений равновесия статики, тогда такая задача не может быть решена приемами статики и называется задачей статически неопределимой.

Определение неизвестных реакций связей выясним на отдельных примерах.

Задача №1

Два одинаковых однородных цилиндра весом Q = 60 кГ каждый (рис. 57, а) соприкасаются между собой в точке В и удерживаются в равновесии двумя вертикальными и горизонтальной плоскостями. Радиус каждого из цилиндров равен а. Пренебрегая трением между цилиндрами и плоскостями, найти реакции 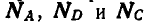в точках A, D и С соприкасания цилиндров и плоскостей.

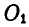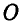Решение. Соединяя центры цилиндров и прямой, заключаем, что прямая 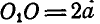составляет с горизонтальной прямой 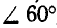, так как проекция 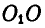на горизонталь равна а.

Рассмотрим сначала равновесие верхнего цилиндра (рис. 57, б):.

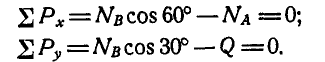
Отсюда получаем: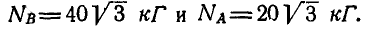

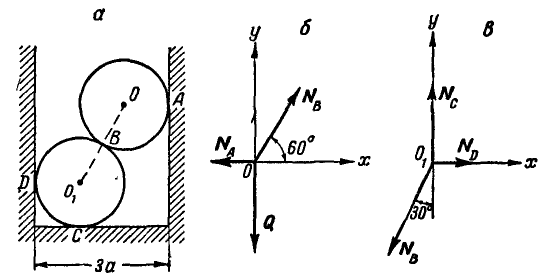
Рис. 57.

Обе реакции получились, со знаком 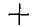, следовательно направлением их стрелок мы задались правильно. При рассмотрении равновесия нижнего цилиндра известная уже нам сила 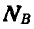по закону «действие равно противодействию» должна быть направлена в противоположную сторону (рис. 57, в):

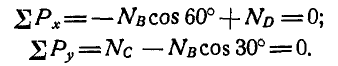
Отсюда получаем: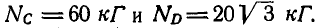

Эту задачу можно было бы решить геометрическим способом, построив треугольники равновесия для каждого из цилиндров.

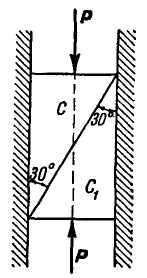
Рис. 58.

Задача №2

При каком наибольшем и наименьшем угле 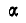возможно равновесие грузов Q и Р, расположенных на призме (рис. 59, а), если Q = 2P и коэффициент трения грузов о призму равен ?

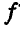Решение. Рассмотрим сначала предельный случай равновесия грузов Р и Q, когда 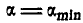; при этом силы трения 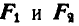грузов о плоскость будут направлены в сторону, обратную направлению их возможного движения. Схема сил, действующих на грузы, представлена на рисунке 59, б.

Уравнения равновесия груза Р будут:

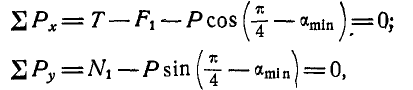, где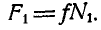 

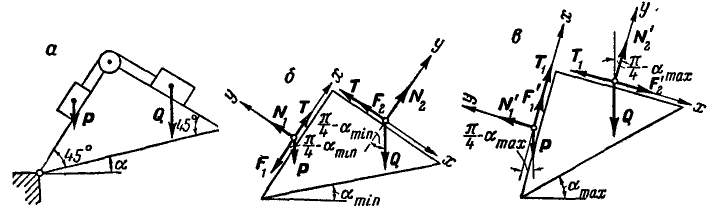
Рис. 59.

Точно так же уравнения равновесия для груза Q будут:

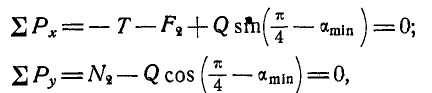 где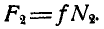 

Подставляя вместо 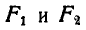и их значения, имеем:

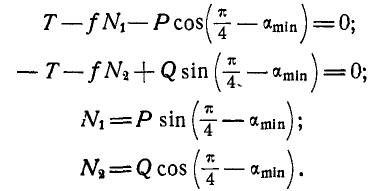
Складывая первые два уравнения и подставляя вместо 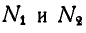 их значения, получим:

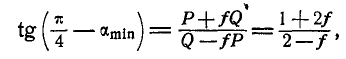
или

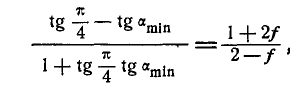
откуда

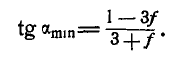
Для нахождения 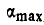, при котором возможно равновесие грузов, придется силы трения 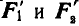, направить в противоположную сторону (рис. 59, в). Составляя в этом случае, как и в предыдущем, уравнения равновесия для каждого из грузов, получим окончательно:

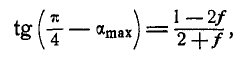
или

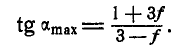
Задача №3

Два однородных бруска AD и СВ одинаковой длины и одинакового веса Q=60 кГ каждый наклонены к горизонтальной прямой под 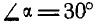(рис. 60, а). В точке С брусок СВ опирается на стержень AD, который, в свою очередь, опирается в точке D на горизонтальную плоскость. Пренебрегая трением, найти реакции в неподвижных шарнирах А и В и в точке D, если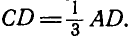

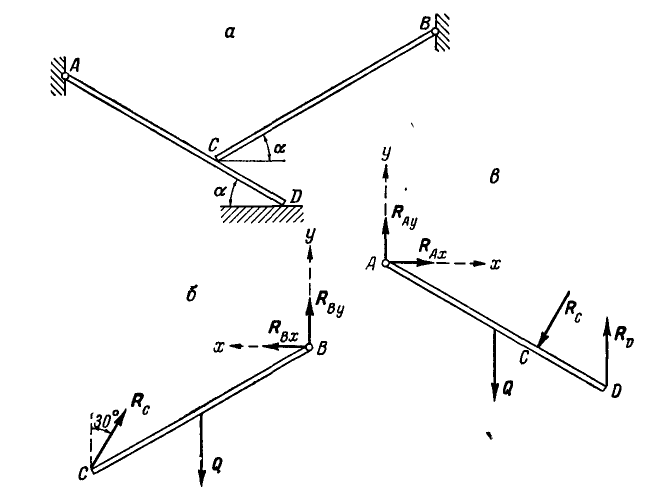
Рис. 60.

Решение. Рассмотрим равновесие каждого из брусков в отдельности. Составляя сначала уравнения равновесия сил для бруска СВ (рис. 60, б), имеем:

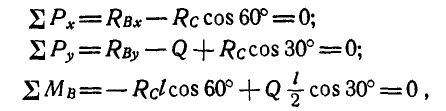
а затем для бруска AD (рис. 60, в):

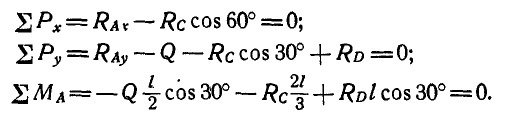
Длина бруска 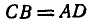обозначена через .

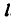После решения уравнений получаем:

• Заказать решение задач по теоретической механике

Задача №4

Однородный цилиндр весом Q = 60 кГ опирается свободно на вертикальную и наклонную плоскости АВ и ВС (рис. 61, а). В точках А и С плоскости опираются на гладкие опоры, расположенные на одной горизонтали. Найти давления 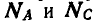в точках А и С, пренебрегая трением цилиндра о плоскости.

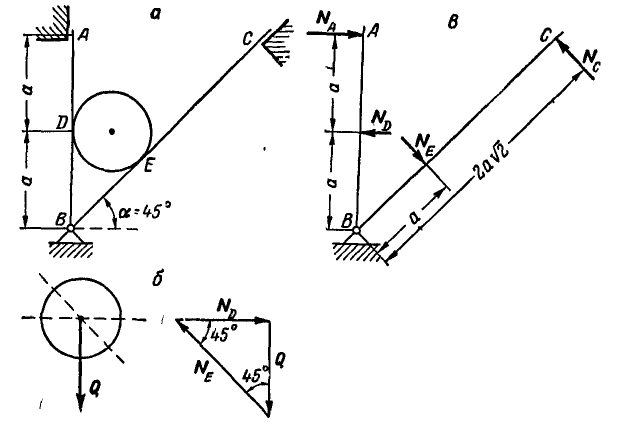
Рис. 61

Решение. Рассмотрим сначала равновесие цилиндра (рис. 61, б) и, построив для него треугольник равновесия, находим: 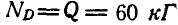 и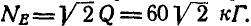

Теперь уже можно перейти к рассмотрению равновесия плоскостей ВА и ВС (рис. 61, в). Для определения давлений в точках А и С освободимся от связей и взамен них введем реакции 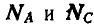. Равновесие каждой из плоскостей, имеющих ось вращения в точке В, будет возможно, если силы, действующие на плоскости, не смогут их вращать, а это будет при условии, если сумма моментов всех сил, приложенных к каждой из плоскостей относительно оси вращения В, равна нулю, т. е.:

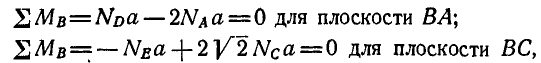
откуда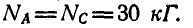

Мы нашли реакции связей в точках А и С; давления же в этих точках, численно равные реакциям связей, будут направлены в противоположные реакциям 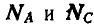стороны.

Задача №5

Система состоит из трек однородных квадратных пластинок I, II и III, соединенных в точках А, В, С и D шарнирно (рис. 62, а). Вес каждой из пластинок II и III равен Q кГ. Зная, что веса пластинок пропорциональны их площадям, найти реакции связей в шарнирах С и D, пренебрегая трением.

Решение. Общее число неизвестных сил равно девяти, так как каждый из неподвижных шарниров А, В, С и D дает по две неизвестные составляющие реактивные силы, а девятая реактивная сила, известная по направлению, возникает в точке Е, Для определения девяти неизвестных необходимо иметь девять уравнений, которые мы получим, если рассмотрим в отдельности равновесие каждой из пластинок I, II и III (рис. 62, б).

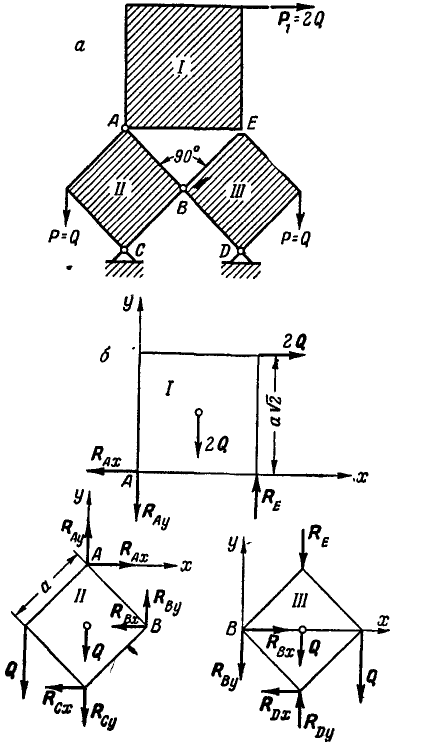
Рис. 62.

На чертеже указано направление действующих на каждую из пластинок сил.

Составляя для каждой из пластинок по три уравнения равновесия, имеем:

для пластинки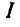

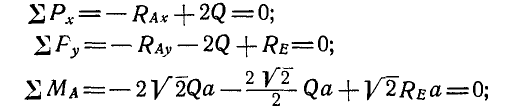
для пластинки 

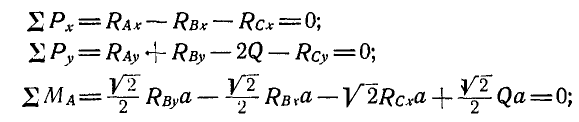
для пластинки

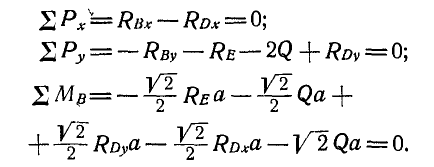
Решая полученные девять уравнений с девятью неизвестными, находим:

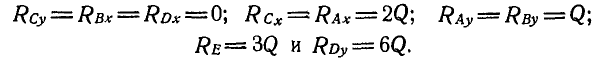
Все модули реакций получились со знаком плюс. Если бы некоторые из найденных модулей получились со знаком минус, то направление стрелок соответствующих реакций пришлось бы изменить на обратное тому, которое было принято при решении задачи.