
Равновесие сходящихся сил в теоретической механике
Равновесие сходящихся сил:
При определении равнодействующей системы пяти сил в задаче установлено, что 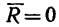
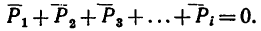
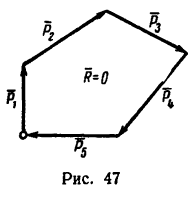
Из геометрического условия следует аналитическое условие равновесия, выражающееся двумя уравнениями:
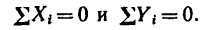
Следует заметить, что все задачи, приведенные в § 6-2, можно решить с применением условия равновесия системы сходящихся сил. Причем при решении задач на равновесие системы сходящихся сил можно использовать те же три метода: графический, графо-аналитический и аналитический (метод проекций).
Необходимо учитывать, что если рассматривается равновесие плоской системы сходящихся сил, приложенных к одному телу, число неизвестных величин не должно превышать двух (условие статической определимости задачи с плоской системой сходящихся
сил):
- а) неизвестна одна сила, т. е. ее модуль и направление;
- б) неизвестны направления двух сил данной системы;
- в) неизвестны модуль одной из сил и направление второй;
- г) неизвестны модули двух сил.
При графическом методе решения во всех четырех случаях можно построить замкнутый силовой многоугольник и найти в нем неизвестные величины.
Графо-аналитический метод целесообразно применять в тех случаях, когда рассматривается равновесие трех сил. При этом по условию задачи в произвольном масштабе строится замкнутый треугольник, который затем решается на основе геометрических либо тригонометрических соотношений.
Метод проекций целесообразно применять для решения задач с числом сил больше трех.
При решении задач на равновесие плоской системы сходящихся сил рекомендуется придерживаться такой общей для всех систем схемы:
- а) выделить тело или точку, равновесие которых рассматривается в данной задаче, и изобразить их на рисунке;
- б) выяснить, какие нагрузки действуют на тело (точку) и также изобразить их на рисунке;
- в) освободить выделенное тело (точку) от связей и заменить их действие реакциями, которые надо изобразить на том же рисунке;
- г) на основе полученной схемы сил построить замкнутый силовой треугольник (если рассматривается равновесие трех сил) или составить уравнения равновесия; причем при составлении уравнений проекций оси целесообразно расположить так, чтобы их направления были параллельны или перпендикулярны к искомым силам (оси проекций также показываются на рисунке);
- д) после решения уравнений равновесия полученные результаты необходимо проверить либо при помощи неиспользованных уравнений или соотношений, либо путем решения задачи другим способом.
Задача №1
Фонарь весом 9 кГ подвешен на кронштейне АВС (рис. 48, а). Определить реакции горизонтального стержня АВ и наклонной тяги ВС, если АВ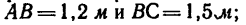 крепления в точках А, В и С шарнирные.
крепления в точках А, В и С шарнирные.
Решение —графо-аналитическим методом с применением геометрических соотношений.
1. В данном случае на шарнир В действуют три силы; вес фонаря G (рис. 48, 6) и реакции стержней 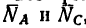 направленные вдоль стержней.
направленные вдоль стержней.
Заметим, что стержень АВ сжат, значит реакция 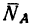 направлена от стержня к шарниру, а стержень ВС растянут, поэтому реакция
направлена от стержня к шарниру, а стержень ВС растянут, поэтому реакция 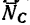 направлена от шарнира к стержню. Шарнир В с действующими на него силами изобразим отдельно.
направлена от шарнира к стержню. Шарнир В с действующими на него силами изобразим отдельно.
2. Так как шарнир В под действием этих трех сил находится в равновесии, силовой треугольник, составленный из них, должен быть замкнутым.
Выберем произвольную точку D (рис. 48, в) и отложим от нее отрезок DE, изображающий силу G. Из точек Е и D проведем прямые EF и DF, параллельные соответственно АВ и СВ. В полученном треугольнике DEF сторона EF изображает реакцию 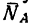 (реакцию стержня АВ) и сторона FD—реакцию
(реакцию стержня АВ) и сторона FD—реакцию 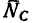 (реакцию стержня ВС)*.
(реакцию стержня ВС)*.
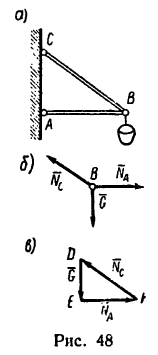
3. Так как в условии задачи даны линейные размеры кронштейна, величины сил 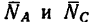 наиболее просто определить исходя из подобия треугольников АВС и EFD:
наиболее просто определить исходя из подобия треугольников АВС и EFD:
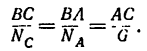
Отсюда
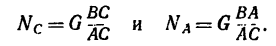
4. Неизвестную в задаче длину АС определяем по теореме Пифагора:
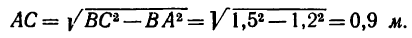
* Если все указанные в п. 2 построения выполнить в определенном масштабе, а затем измеренные длины FF и FD умножить на масштаб построения, то получим решение задачи графическим методом.
5. Окончательно
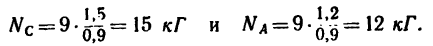
Задача №2
В точке В кронштейна АВС (рис. 49, а) подвешен груз М массой 816 кг. Определить реакции стержней кронштейна, если углы кронштейна 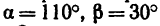 и крепления в точках А, В и С шарнирные.
и крепления в точках А, В и С шарнирные.
Решение 1— графоаналитическим методом с применением тригонометрических соотношений.
1. На точку В кронштейна действуют три силы: вес груза 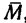 , равный G = mg = 816*9,81 = 8000 н
, равный G = mg = 816*9,81 = 8000 н 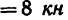 реакции стержней
реакции стержней 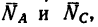 действующие вдоль стержней (рис. 49, б).
действующие вдоль стержней (рис. 49, б).
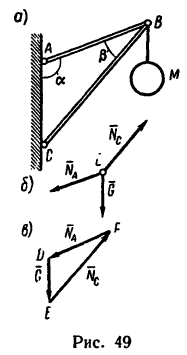
2. Так как эти три силы образуют уравновешенную систему, то составленный из них треугольник должен быть замкнутым (рис. 49, в — построение 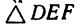 произведено в том же порядке, как в задаче 39-8).
произведено в том же порядке, как в задаче 39-8).
3. 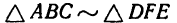 потому, что
потому, что
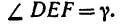 Применив к
Применив к 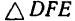 теорему синусов, имеем
теорему синусов, имеем
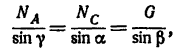
откуда
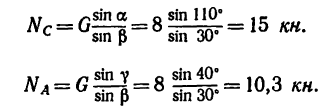
Решение 2—методом проекций при помощи уравнений равновесия.
1. Так как три силы 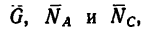 действующие на точку В (рис. 50), образуют уравновешенную систему, то алгебраические суммы проекций этих сил на каждую из двух осей координат равны нулю.
действующие на точку В (рис. 50), образуют уравновешенную систему, то алгебраические суммы проекций этих сил на каждую из двух осей координат равны нулю.
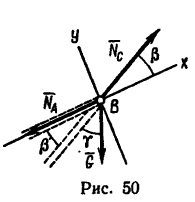
2. Выберем оси координат так, чтобы одна из осей совпадала с линией действия одной из неизвестных сил (см. рис. 50), и составим два уравнения проекций:
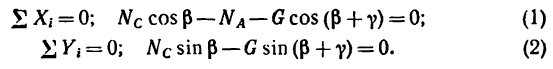
Из уравнения (2)
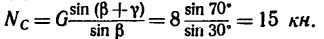
Из уравнения (1)
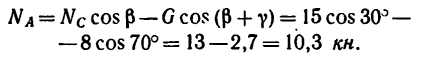
Как видно, ответ получается тот же.
После решения задач, аналогичных 39-8 и 40-8, можно сделать ошибочный вывод, что силовой треугольник и треугольник, образованный стержнями кронштейна, должны быть подобными. Но это совсем не обязательно. В этом легко убедиться, рассмотрев следующую задачу.
Задача №3
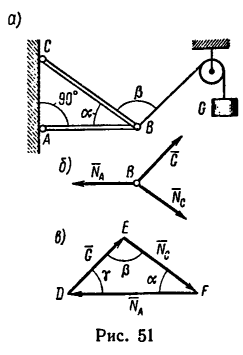
К шарниру В кронштейна АВС прикреплена веревка, перекинутая через блок, к другому концу которой прикреплен груз весом G= 1,5 кн (рис. 51. а).
Определить усилия в стержнях АВ и СВ кронштейна, если крепления в точках А и С шарнирные, а = 35° и 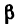 =100°.
=100°.
Решение 1-графо-аналитическим методом с применением тригонометрических соотношений.
1. На шарнир В в направлении к блоку действует натяжение веревки, равное весу груза G, и вызывает появление двух усилий, направленных вдоль стержней.
При этом стержень АВ растягивается, а стержень СВ сжимается.
Так как рассматривается равновесие шарнира В, то отбросим стержни, заменив их реакциями 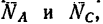 приложенными к шарниру. Изобразим шарнир вместе с тремя силами на рис. 51, б.
приложенными к шарниру. Изобразим шарнир вместе с тремя силами на рис. 51, б.
2. Силы G, 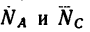 образуют уравновешенную систему, значит построенный из них треугольник является замкнутым (рис. 51, в). Как видим,
образуют уравновешенную систему, значит построенный из них треугольник является замкнутым (рис. 51, в). Как видим, 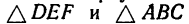 в данной задаче не подобны друг другу;
в данной задаче не подобны друг другу; 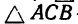 — прямоугольный, а в
— прямоугольный, а в 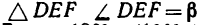 = 100°,
= 100°,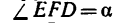 = 35° и, следовательно,
= 35° и, следовательно, 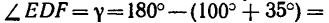 45°.
45°.
3. Применив к 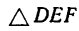 теорему синусов, получим
теорему синусов, получим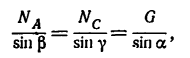
откуда
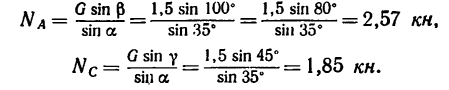
Решение 2—методом проекций.
1. Изобразив шарнир В вместе с действующими на него силами 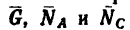 и расположив оси проекций, как показано на рис. 52, составим уравнения равновесия:
и расположив оси проекций, как показано на рис. 52, составим уравнения равновесия:
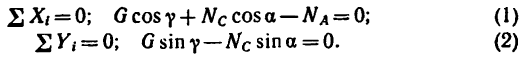
2. Из уравнения (2)
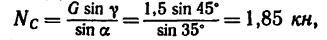
а из уравнения (1)
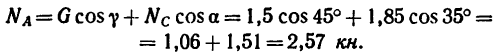
Как и следовало ожидать, оба решения дают одинаковый результат. Реакции стержней (их действия на шарнирный болт В) равны 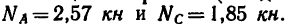 Точно с такими же усилиями действует шарнирный болт на стержни. Стержень АВ растянут силой 2,57 кн, а стержень СВ сжат силой 1,85 кн.
Точно с такими же усилиями действует шарнирный болт на стержни. Стержень АВ растянут силой 2,57 кн, а стержень СВ сжат силой 1,85 кн.
В связи с решением подобных задач методом проекций необходимо отметить следующее. Применяя метод проекций к определению равнодействующей любого числа сходящихся сил, наиболее удобно использовать обычную прямоугольную систему координатных осей. При этом найденные проекции равнодействующей и искомая равнодействующая образуют прямоугольный треугольник, решая который легко определить модуль и направление равнодействующей.
Применяя метод проекций к решению задач на равновесие сил, совсем не обязательно использовать взаимно перпендикулярные оси.
В тех случаях, когда определяются модули сил, направления которых заданы (как в задачах, каждую из осей целесообразно расположить перпендикулярно к направлению искомых сил. Тогда в каждое уравнение равновесия войдет только одно неизвестное.
Решим таким образом ту же задачу 41-8.
1. Изобразим шарнирный болт В с действующими на него силами (рис. 53).
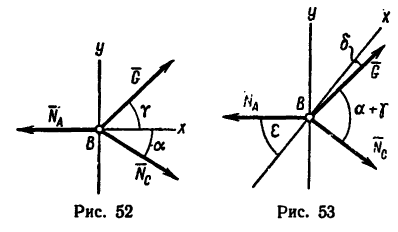
Расположим ось х перпендикулярно 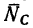 и составим первое уравнение равновесия:
и составим первое уравнение равновесия:
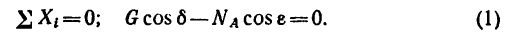
2. Замечая, что 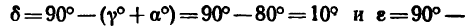
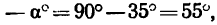 из уравнения (1)
из уравнения (1)
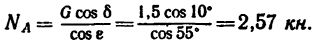
3. Расположим вторую ось (ось у) перпендикулярно к направлению силы 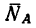 и составим второе уравнение:
и составим второе уравнение:
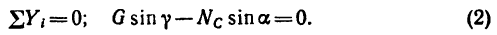
4. Из уравнения (2)
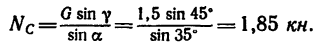
Возможность произвольного расположения осей проекций позволяет производить проверку решения задачи. Чтобы проверить правильность решения задачи, проведенного любым способом, следует выбрать расположение оси таким образом, чтобы на нее спроектировались обе найденные силы. При правильном решении сумма проекций на вновь выбранную ось получится равной нулю. Если же сумма не равна нулю, нужно искать допущенную в решении ошибку.
Задача №4
При помощи стержневого устройства АВС (в точках А, В и С соединения шарнирные) удерживаются в равновесии
два груза — первый весом 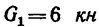 и второй весом (
и второй весом (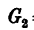 =8 кн. Угол
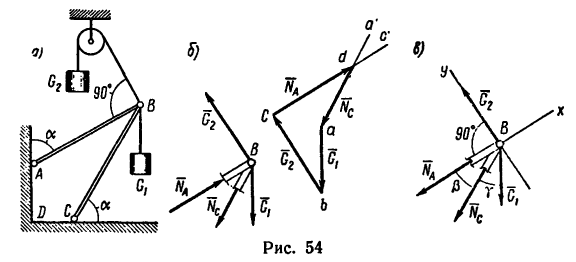
=8 кн. Угол 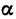 = 60° (рис. 54). Определить усилия, которые испытывают стержни АВ и ВС.
= 60° (рис. 54). Определить усилия, которые испытывают стержни АВ и ВС.
В этой задаче на шарнир В действуют уже не три, а четыре силы, поэтому решать задачу графо-аналитическим методом не имеет смысла — решение получится слишком длинным.
Когда на устройство, состоящее из двух стержней, действует одна нагрузка (как в задачах 38-8, 40-8 и 41-8), то можно легко определить, какой из стержней растянут и какой сжат.
В данной задаче это сразу определить нельзя, так как груз 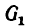 сжимает стержень ВС и растягивает АВ, а груз
сжимает стержень ВС и растягивает АВ, а груз 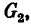 , наоборот, растягивает стержень ВС и сжимает АВ.
, наоборот, растягивает стержень ВС и сжимает АВ.
При решении задачи графическим методом направления усилий в стержнях определяют следующим образом.
Выбрав масштаб сил, из произвольной точки а построим отрезок ab, изображающий вектор 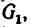 затем из точки b построим отрезок bс, изображающий вектор
затем из точки b построим отрезок bс, изображающий вектор 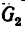 (построение в масштабе рекомендуется выполнить самостоятельно). Из точек с и а проведем прямые
(построение в масштабе рекомендуется выполнить самостоятельно). Из точек с и а проведем прямые 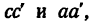 параллельные стержням АВ и СВ, которые пересекутся в точке d.
параллельные стержням АВ и СВ, которые пересекутся в точке d.
Получается замкнутый силовой четырехугольник abcd (рис. 54, б), в котором стороны cd и da изображают соответственно реакции 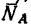 (направлена от с к d) и Ус (направлена от d и а). Если теперь эти реакции стержней мысленно приложить к шарниру В со стороны стержней (как реакции стержней—см. на рис. 54, б слева), то:
(направлена от с к d) и Ус (направлена от d и а). Если теперь эти реакции стержней мысленно приложить к шарниру В со стороны стержней (как реакции стержней—см. на рис. 54, б слева), то:
- 1) реакция
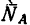 действует на шарнир в направлении от стержня к шарниру — значит стержень АВ сжат;
действует на шарнир в направлении от стержня к шарниру — значит стержень АВ сжат; - 2) реакция
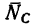 действует на шарнир в направлении от шарнира к стержню —значит стержень СВ растянут.
действует на шарнир в направлении от шарнира к стержню —значит стержень СВ растянут.
При решении методом проекций нет необходимости заранее определять, в какую сторону направлены реакции вдоль стержней. Целесообразнее предположить, что под действием нагрузки все стержни растянуты (т. е. их реакции направлены от шарнира, равновесие которого рассматриваем, к стержням). Затем выбрать оси проекций, составить уравнения равновесия и решить их. У действительно растянутых стержней модули их реакций получатся положительными (предположительное направление реакций совпадает с действительным), а у сжатых стержней модули их реакций получатся отрицательными (предположительное направление реакций противоположно действительному).
Учитывая изложенное выше, приступим к решению задачи.
Решение—методом проекций.
1. Изобразим шарнир В с действующими на него нагрузками 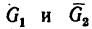 и реакциями стержней Уд (реакция стержня АВ) и
и реакциями стержней Уд (реакция стержня АВ) и 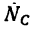 (реакция стержня СВ), как показано на рис. 54, в, т. е. считаем предварительно, что оба стержня растянуты.
(реакция стержня СВ), как показано на рис. 54, в, т. е. считаем предварительно, что оба стержня растянуты.
2. Совместим оси проекций с силами 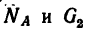 и составим уравнения равновесия:
и составим уравнения равновесия:
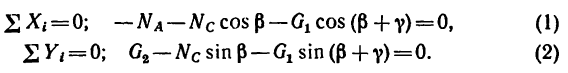
3. Прежде чем приступить к решению уравнений, нужно найти углы 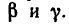
Угол 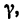 образуемый вектором
образуемый вектором 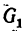 и стержнем ВС, легко найти по рис. 54, а. Так как а = 60°, a
и стержнем ВС, легко найти по рис. 54, а. Так как а = 60°, a 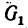 направлен по вертикали, то
направлен по вертикали, то 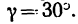 . Угол
. Угол 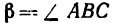 (рис. 54, а). Так как в любом четырехугольнике сумма внутренних углов равна 360°, то
(рис. 54, а). Так как в любом четырехугольнике сумма внутренних углов равна 360°, то 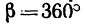
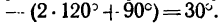 . Значит
. Значит 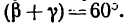
4. Из уравнения (2)
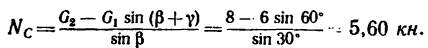
Таким образом, стержень ВС растянут силой 5,60 кн. Из уравнения (1)
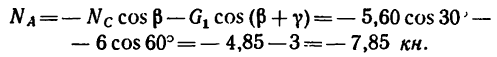
Следовательно, стержень АВ сжат силой 7,85 кн.
Задача №5
Каждую силу Р нужно дополнительно приложить к шарниру В стержневого устройства, описанного в задаче 42-8, чтобы оба стержня АВ и СВ были растянуты усилиями 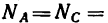 7,85 кн.
7,85 кн.
Решение—методом проекций.
1. Используя рис. 54, айв, изобразим шарнир В с действующими на нем силами 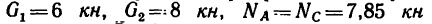 и предположим, что искомая сила Р образует с осью х угол
и предположим, что искомая сила Р образует с осью х угол 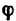 (рис. 55).
(рис. 55).
2. Составим уравнения равновесия:
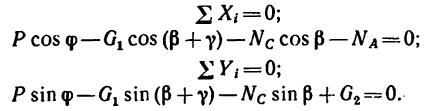
3. В каждое из уравнений входят обе неизвестные величины — модуль силы 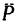 и угол
и угол 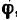 , определяющий ее направление. Одно из неизвестных нужно исключить из этих уравнений. В данном случае это можно сделать, если представить уравнения в виде
, определяющий ее направление. Одно из неизвестных нужно исключить из этих уравнений. В данном случае это можно сделать, если представить уравнения в виде
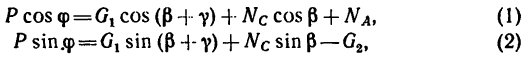
а потом уравнение (2) разделить на уравнение (1):
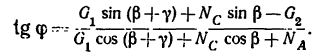
Отсюда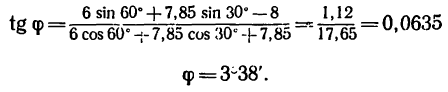
4. Подставив найденное значение угла 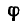 в любое из уравнений равновесия, найдем значение Р.
в любое из уравнений равновесия, найдем значение Р.
Из уравнения (2)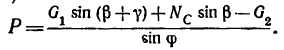
Так как числитель этого выражения определен в п. 3 и равен 1,12, а знаменатель 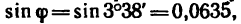 то
то
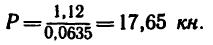
Таким образом, для того чтобы оба стержня были растянуты с одинаковыми усилиями по 7,85 кн, к шарниру В необходимо добавить силу 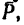 , модуль которой Р = 17,65 кн и которая направлена под углом
, модуль которой Р = 17,65 кн и которая направлена под углом 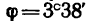 к положительному направлению оси х или под углом
к положительному направлению оси х или под углом 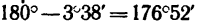 к стержню ВА.
к стержню ВА.
Задачу 43-8 можно было решить по примеру задач, приведенных в § 7-2. Для четырех заданных сил 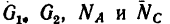 найти равнодействующую R, а затем добавить к ним силу
найти равнодействующую R, а затем добавить к ним силу 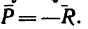
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |