
Равнопеременное вращательное движение в теоретической механике
Равнопеременное вращательное движение:
Вращательное движение с переменной угловой скоростью называется неравномерным. Если же угловое ускорение 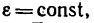

и уравнение, выражающее угловую скорость тела в любой момент времени,

представляют совокупность основных формул вращательного равнопеременного движения тела.
В эти формулы входят всего шесть величин: три постоянных для данной задачи 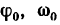 и
и 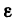 и три переменных
и три переменных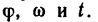 Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин.
Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин.
Для удобства решения некоторых задач из уравнений (1) и (2) можно получить еще две вспомогательные формулы.
Исключим из (1) и (2) угловое ускорение 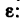

Исключим из (1) и (2) время t:

В частном случае равноускоренного вращения, начавшегося из состояния покоя, 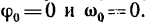 Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид:
Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид:
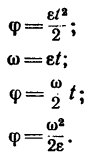
Задача №1
Маховик, вращающийся с угловой скоростью  = 90 об/мин, с некоторого момента начинает вращаться равноускоренно и через 1,5 мин достигает угловой скорости
= 90 об/мин, с некоторого момента начинает вращаться равноускоренно и через 1,5 мин достигает угловой скорости 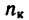 = — 150 об/мин. Определить угловое ускорение маховика. Сколько всего оборотов делает маховик за 1,5 мин? Какую скорость имеют точки на цилиндрической поверхности маховика через 45 сек после начала равноускоренного движения, если диаметр маховика 1,2 м?
= — 150 об/мин. Определить угловое ускорение маховика. Сколько всего оборотов делает маховик за 1,5 мин? Какую скорость имеют точки на цилиндрической поверхности маховика через 45 сек после начала равноускоренного движения, если диаметр маховика 1,2 м?
Решение 1. Все угловые величины выражаем в радианном измерении.
1. Если 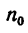 =90 об/мин, то
=90 об/мин, то
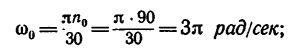
если 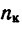 =150 об/мин, то
=150 об/мин, то
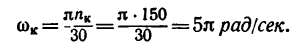
2. Из уравнения (2) находим угловое ускорение, учитывая, что изменение угловой скорости от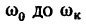 происходит за t=1,5 мин = 90 сек:
происходит за t=1,5 мин = 90 сек:
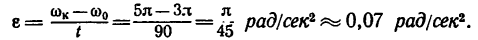
3. Определяем из формулы (3) угол поворота тела за t = 1,5 мин = 90 сек, принимая 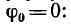
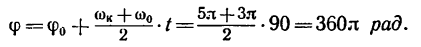
4. Находим, какому числу оборотов соответствует этот угол поворота:
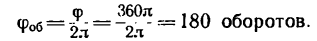
Следовательно, за время равноускоренного вращения маховик успеет совершить 180 оборотов.
5. Прежде чем найти по формуле
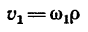
скорость точек на ободе маховика в момент времени t=45 сек после начала равноускоренного вращения, необходимо найти угловую скорость маховика  в этот момент:
в этот момент:
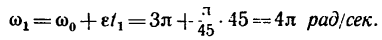
Зная, что 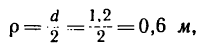 получаем
получаем
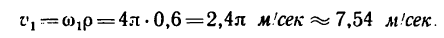
Решение 2—угловые величины выражаются в оборотах, а время — в сек (t=1,5 мин — 90 сек).
1. Выражаем данные угловые скорости в об/сек.
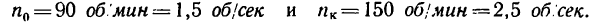
2. Представим формулу (3) в ином виде, приняв 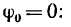
Тогда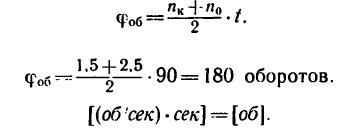
3. Обозначив 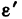 —угловое ускорение, выраженное через обороты, формулу (2) можно представить в виде
—угловое ускорение, выраженное через обороты, формулу (2) можно представить в виде
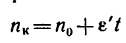
и тогда
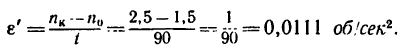
4. Найдем 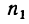 — угловую скорость маховика через
— угловую скорость маховика через 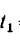 = 45 сек после начала равноускоренного вращения:
= 45 сек после начала равноускоренного вращения:
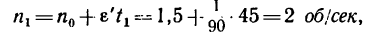
что соответствует
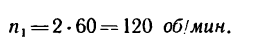
Теперь находим при этой угловой скорости маховика скорость точек на его ободе:
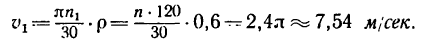
Если же 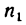 выражено в об/сек, то
выражено в об/сек, то
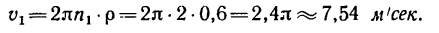
Задачу можно решить и не переводя заданное время из минут в секунды, т. е. решить при заданных числовых величинах
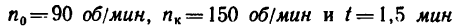 Этот вариант решения рекомендуем выполнить самостоятельно
Этот вариант решения рекомендуем выполнить самостоятельно
Задача №2
Вал, вращающийся равноускоренно из состояния покоя, в первые 12 сек совершает 95,5 оборота. С каким угловым ускорением вращается вал и какую угловую скорость он приобретает?
Решение.
1. Угловое перемещение за время t=12 сек равноускоренного движения составляет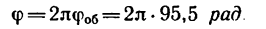
2. Из формулы (5) находим угловое ускорение вала:
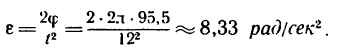
3. К концу 12-й секунды вал приобретает угловую скорость [см. формулу (6)):
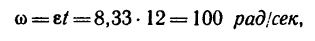
что соответствует
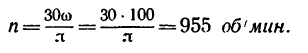
Задачу можно решить и в другой последовательности, а также выражая величины через обороты.
Задача №3
Колесо, вращающееся со скоростью 1500 об/мин, при торможении начинает вращаться равнозамедленно и через 30 сек останавливается. Определить угловое ускорение и число оборотов колеса с момента начала торможения до остановки.
Решение.
1. Выразим начальную угловую скорость в рад/сек:
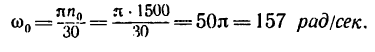
Найдем угловое ускорение из формулы (2):
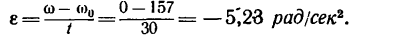
2. Представим формулу (3) в виде
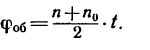
Тогда число оборотов вала за t = 30 сек — 0,5 мин
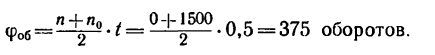
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Неравномерное вращательное движение
- Плоскопараллельное движение тела
- Определение передаточных отношений различных передач
- Задачи на поступательное движение тела
- Неравномерное движение точки по любой траектории
- Определение траектории, скорости и ускорения точки
- Кинематический способ определения радиуса кривизны траектории
- Равномерное вращательное движение