Равнопеременное движение точки в теоретической механике

Равнопеременное движение точки:

Если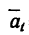

Если же постоянным остается только числовое значение касательного уравнения

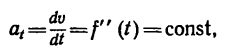
то 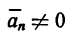и такое движение точки называется равнопеременным криволинейным.

При 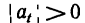движение точки называется равноускоренным, а при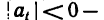равнозамедленным.

Уравнение равнопеременного движения независимо от его траектории имеет вид (см. § 63 в учебнике Е. М. Никитина)

Здесь 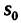—расстояние точки от исходного положения в момент начала отсчета; 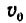—начальная скорость и 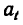— касательное ускорение-величины численно постоянные, а s и t — переменные.

Числовое значение скорости точки в любой момент времени определяется из уравнения

Уравнения (1) и (2) являются основными формулами равнопеременного движения и они содержат шесть различных величин: три постоянные: 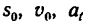и трн переменные: s, v, t.

Следовательно, для решения задачи на равнопеременное движение точки в ее условии должно быть дано не менее четырех величин (систему двух уравнений можно решить лишь в том случае, если они содержат два неизвестных).

Если неизвестные входят в оба основных уравнения, например, неизвестны 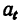и t, то для удобства решения таких задач выведены вспомогательные формулы:

после исключения 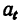из (1) и (2)

после исключения t из (1) и (2)

В частном случае, когда начальные величины 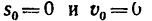(равноускоренное движение из состояния покоя), то получаем те же формулы в упрощенном виде:

Уравнения (5) и (6) являются основными, а уравнения (7) и (8) — вспомогательными.

Равноускоренное движение из состояния покоя, происходящее под действием только силы тяжести, называется свободным падением. К этому движению применимы формулы (5) —(8), причем

Задача №1

Шарик, размерами которого можно пренебречь, начинает скатываться по наклонной плоскости из состояния покоя. Через 20 сек после начала движения шарик находится от исходного положения на расстоянии 6 м.

Определить ускорение шарика и его скорость в конце 10-й и 20-й сек, а также расстояние, пройденное шариком за первые 10 шс.

Решение.

1.    Из условия задачи следует, что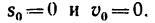 Пройденное за 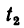—20 сек расстояние 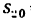= 6 м. Даны четыре величины. Требуется определить ускорение шарика (движение прямолинейное, значит определить нужно только 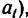скорости 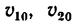и расстояние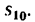

2.    Найдем из формулы (7) скорость шарика, которую он приобретает в конце 20-й сек:

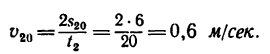
3.    Найдем из формулы (6) ускорение шарика, которое он имеет, двигаясь по наклонной плоскости:

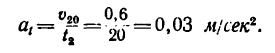
4.    Теперь из этой же формулы (6) можно найти скорость в конце

10-й сек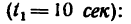

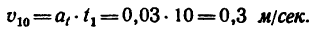
5.    Из формулы (5) находим расстояние, пройденное точкой за первые 10 сек:

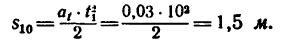
Задачу можно решить в ином порядке. Сначала из формулы (5) определить ускорение

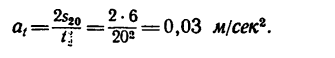
Затем из формулы (6) определить 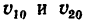и, наконец, из формулы (5) найти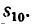

Задача №2

Автомобиль, движущийся равномерно и прямолинейно со скоростью 60 км/ч, увеличивает в течение 20 сек скорость до 90 км/ч. Определить, какое ускорение получит автомобиль и какое расстояние он проедет за это время, считая движение рарноускоренным.

Решен и е.

1.    Здесь также четыре данных величины:

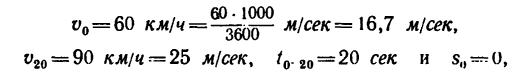
так как движение автомобиля рассматривается только на том участке траектории (дороги), где он движется с ускорением.

2.    Из вспомогательной формулы (3), полагая в ней 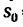=0, найдем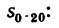

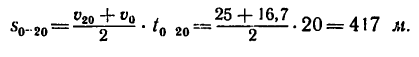
3.    Из формулы (2) найдем ускорение, полученное автомобилем:

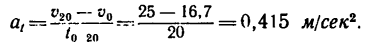
Задачу можно решить несколько иным путем. Сначала из формулы (2) найти ускорение автомобиля, а затем из формулы (1) найти пройденное расстояние.

Задача №3

Имея скорость 20 м/сек, автомобиль въезжает на криволинейный участок дороги, имеющий радиус закругления 200 м. За 40 сек равнопеременного движения он проезжает расстояние 400 м.

Определить, с каким касательным ускорением движется автомобиль, какова его скорость в конце пройденных 400 м и каково полное ускорение на середине этого пути.

Решение.

1.    Изобразим участок дороги, по которой движется автомобиль (рис. 197): О — начало участка, В— конец участка и А—его середина.

Для равнопеременного движения в задаче имеется четыре основных данных: 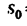—0 (так как за начало отсчета движения принимаем точку 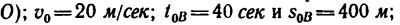кроме того, известен радиус закругления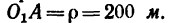

2.    Из формулы (3) найдем скорость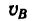в конце участка дороги длиной 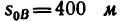(полагая, что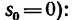

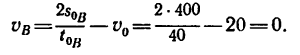
В конце рассматриваемого участка автомобиль останавливается, значит движение равнозамедленное *.

3.    Найдем касательное ускорение автомобиля из формулы (2):

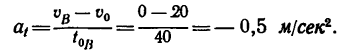
Получившееся отрицательное значение ускорения — подтверждение того, что движение автомобиля равнозамедленное.

4.    Для того чтобы определить полное ускорение автомобиля в середине А участка ОВ, нужно сначала найти скорость 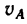— скорость автомобиля в момент прохождения им точки А.

Эту скорость найдем из уравнения (4), приняв 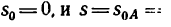200 м:

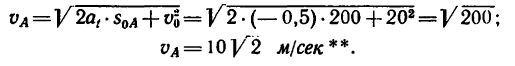
5.    Находим нормальное ускорение автомобиля в точке А:

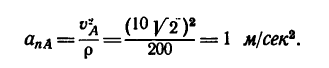
6.    И, наконец, находим полное ускорение автомобиля: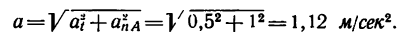

Ускорение получается отрицательным, значит движение равнозамедленное. ** В дальнейшем для определения а„ нужно иметь значение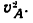

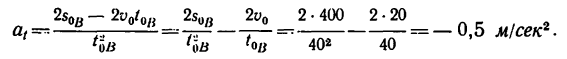
* Решение задачи можно начать с определения касательного ускорения из
формулы (I), считая 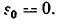Тогда

7.    Вектор полного ускорения 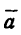направлен к вектору скорости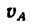

под углом 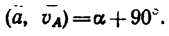Угол а можно найти при помощи его синуса:

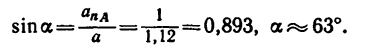
Следовательно,

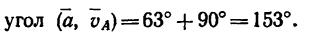
Задача №4

Точка движется в горизонтальной плоскости по заданной траектории ОАВС (рис. 198, а). Начав движение из состояния покоя, точка проходит участок ОА = 300 м равноускоренно за 30 сек, а расстояние от А до В, равное 200 м, она проходит

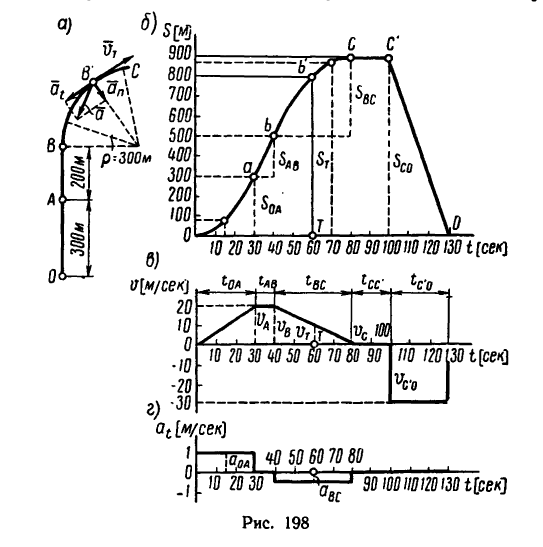
равномерно с той же скоростью, которую имеет в конце участка ОА. Из В точка движется в С уже равнозамедленно и проходит это расстояние за 40 сек. Остановившись в С, точка находится в покое 20 сек, а затем возвращается обратно в О по той же траектории, двигаясь равномерно и затратив на это движение 30 сек.

Построить графики перемещения, скорости и касательного ускорения точки.

Определить полное ускорение точки в момент времени через 60 сек после начала движения.

Решение.

1.    На уяастке О А, длина которого 300 м, точка движется равноускоренно из состояния покоя и проходит этот участок за 30 сек: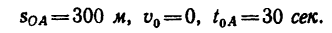

2.    Находим ускорение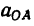 на участке О А из уравнения (5):

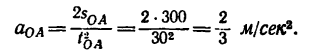
3.    Скорость точки в конце участка О А находим из уравнения (6):

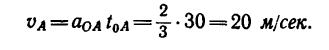
4.    Следующий участок траектории АВ длиной 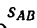=200 м точка проходит с постоянной скоростью 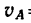= 20 м/сек. Определяем время 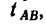затраченное на это движение:

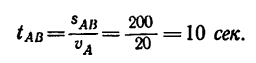
Причем в конце участка АВ скорость 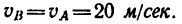Значит, движение на участке ВС точка начинает со скоростью 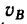= 20 м/сек и, двигаясь равнозамедленно, останавливается в 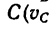= 0) через 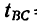= 40 сек.

Длину участка ВС найдем по формуле (3), приняв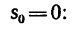

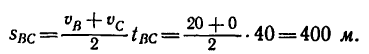
5.    Ускорение аВс точки на участке ВС определяем из формулы (2):

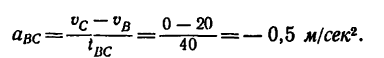
6.В конце траектории точка находится в покое в течение времени

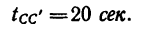
7.    Затем точка движется обратно и проходит равномерно путь

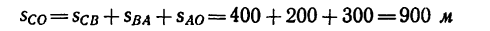
за время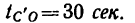

Скорость точки в этом движении

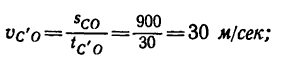
она направлена относительно скоростей первой части движения (например, относительно скоростей 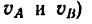в обратную сторону.

8.    На все движение точки по траектории ОАВС в одну и другую сторону вместе с остановкой в конце траектории С 3атрачено 130 сек, которые складываются из времени:

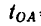• = 30 сек — равноускоренного движения,
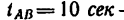• — равномерного движения,
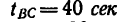• — равнозамедленного движения,
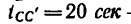• - стояния точки,
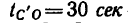• - равномерного обратного движения.

9.    Описанное выше движение точки изображаем графически, построив три графика: перемещений, скоростей и ускорений, расположенных один под другим (рис. 198, б, в, г).

Для построения графиков необходимо выбрать удобные масштабы для времени и остальных величин.

Рекомендуется графики, показанные на рис. 198, вычертить самостоятельно на отдельном листе бумаги в клетку. Масштабы по оси времени на всех трех графиках одинаковы. Масштаб времени / принят равным 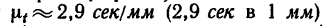и поэтому на графике 130 сек изображаются отрезком, равным 45 мм; масштаб перемещения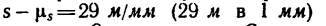и расстояние между началом траектории О и ее концом С, равное 900 м, изображается отрезком, равным 31 мм; масштаб скоростей 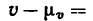2,86 м/сек- мм (2,86 м/сек в 1 мм) и 20 м/сек изображаются отрезком, равным 7 мм, а 30 м/сек - длиной 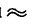10 мм; масштаб ускорений 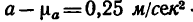мм (0,25 м/сек2 в 1 мм) и 1 изображается отрезком, равным 4 мм, а 0,5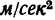 — длиной 2 мм.

При самостоятельном построении этих графиков следует все масштабы увеличить, например принять

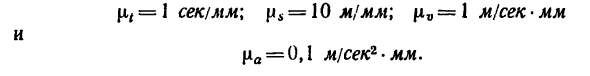
10.    После построения графиков определяем ускорение точки в момент времени Т=60 сек после начала движения (см. условие задачи). Для этого прежде всего на графике перемещения из точки О (начало осей координат) по оси времени откладываем отрезок

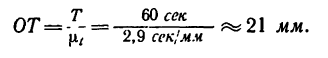
Этот отрезок определит на оси времени время Т = 60 сек (на самостоятельно построенном графике расстояние получится большим:

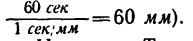
Из точки Т восставим перпендикуляр 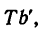измерив его, получим 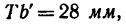значит

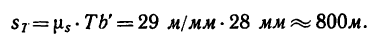
Если это расстояние отложить па траектории, то увидим, что точка в момент времени Т = 60 сек будет находиться на криволинейном участке траектории (положение 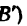с радиусом кривизны р=300 м. Значит ускорение движущейся точки складывается из касательного 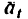и нормального 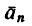ускорений.

Нормальное ускорение

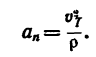
Скорость 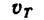в момент времени Т = 60 сек находим из графика скорости:

.
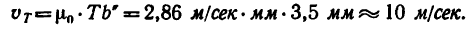
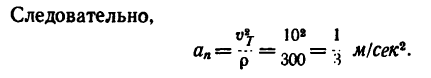Касательное ускорение а, находим из графика ускорений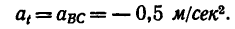

Полное ускорение движущейся точки в момент времени Т = 60 сек

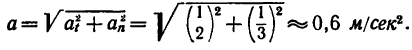
Векторы 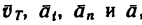характеризующие кинематическое состояние точки в момент времени Т = 60 сек после начала движения, изображены на рис. 198, а.

Задача №5

С крыши высотного дома через каждые 0,5 сек отрываются и свободно падают одна за другой капельки воды.

Определить, через сколько времени после отрыва первой капли расстояние между этой и следующей за ней каплей достигает 7,6 м?

Решение.

1.    Эта задача отличается от предыдущей тем, что в ней рассматривается движение не одной, а сразу двух материальных точек.

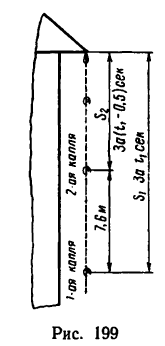
2.    Изобразим перемещение обеих точек (рис. 199). Первая капля за искомое время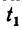, сек успевает пролететь расстояние 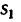м. Вторая капля, начавшая падение через 0,5 сек, находится в падении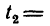 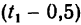сек и успевает за это время пролететь расстояние 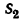м.

3.    Расстояние 7,6 м между каплями через 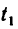сек после начала движения выразим в виде уравнения

Используя формулу (5), получим уравнения падения капель: для первой капли:

для .второй капли

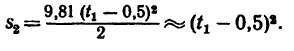
4.    Подставив в уравнение (а) значения 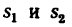из уравнений (б) и (в), получаем уравнение, содержащее лишь одно неизвестное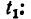

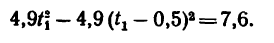
После раскрытия скобок и приведения подобных членов получим:

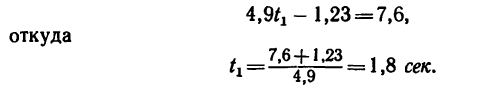
Таким образом, через 1,8 сек после отрыва первой капли или через 1,8-0,5 = 1,3 сек после отрыва второй расстояние между ними будет составлять 7,6 м.