Равномерное вращательное движение в теоретической механике

Вращательное движение твердого тела:

При поступательном движении тела  все его точки движутся по одинаковым траекториям и в каждый данный момент они имеют равные скорости и равные ускорения.

Поэтому поступательное движение тела задают движением какой-либо одной точки, обычно движением центра тяжести.

Рассматривая в какой-либо задаче движение автомобиля (задача 147-29) или тепловоза , фактически рассматриваем движение их центров тяжести.

Вращательное движение тела нельзя отождествить с движением какой-либо одной его точки. Ось любого вращающегося тела (маховика дизеля, ротора электродвигателя, шпинделя станка, лопастей вентилятора и т. п.) в процессе движения занимает в пространстве относительно окружающих неподвижных тел одно и то же место.

Движение материальной точки или поступательное движение тела характеризуют в зависимости от времени линейные величины s (путь, расстояние),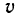

Вращательное движение тела в зависимости от времени t характеризуют угловые величины: 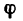(угол поворота в радианах), 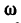(угловая скорость в рад/сек) и 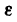(угловое ускорение в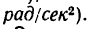

Закон вращательного движения тела выражается уравнением

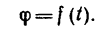
Угловая скорость — величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени

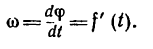
Угловое ускорение - величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости

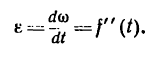
Приступая к решению задач на вращательное движение тела, необходимо иметь в виду, что в технических расчетах и задачах, как правило, угловое перемещение выражается не в радианах 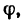а в оборотах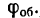

Поэтому необходимо уметь переходить от числа оборотов к ра-дианному измерению углового перемещения и наоборот.
 

Так как один полный оборот соответствует 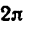рад, то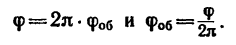

Угловая скорость в технических расчетах очень часто измеряется в оборотах, произведенных в одну минуту (об/мин), поэтому необходимо отчетливо уяснить, что 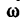рад/сек n об/мин выражают одно и то же понятие - скорость вращения тела (угловую скорость), но в различных единицах - в рад/сек или в об/мин.

Переход от одних единиц угловой скорости к другим производится по формулам

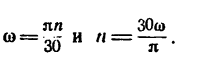
При вращательном движении тела все его точки движутся по окружностям, центры которых расположены на одной неподвижной прямой (ось вращающегося тела). Очень важно при решении задач, приведенных в этой главе, ясно представлять зависимость между угловыми величинами 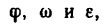характеризующими вращательное движение тела, и линейными величинами  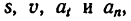характеризующими движение различных точек этого тела (рис 205).

Если р- расстояние от геометрической оси вращающегося тела до какой-либо точки А (на рис. 205 р=ОА), то зависимость между 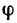- углом поворота пройденным точкой тела за то же вретела и s—расстоянием, мя, выражается так
s—p-
Зависимость между угловой скоростью тела и скоростью точки в каждый данный момент выражается равенством

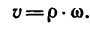
Касательное ускорение точки зависит от углового ускорения и определяется формулой

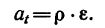
Нормальное ускорение точки зависит от угловой скорости тела и определяется зависимостью

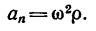
При решении задачи, приведенной в этой главе, необходимо ясно понимать, что вращением называется движение твердого тела, а не точки. Отдельно взятая материальная точка не вращается, а движется но окружности — совершает криволинейное движение.

Равномерное вращательное движение

Если угловая скорость 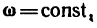то вращательное движение называется равномерным.

Уравнение равномерного вращения имеет вид

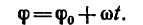
В частном случае, когда начальный угол поворота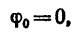

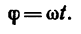
Угловую скорость равномерно вращающегося тела

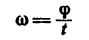
можно выразить и так:

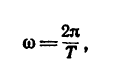
где Т — период вращения тела; 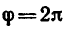—угол поворота за один период.

Задача №1

Маховое колесо вращается равномерно с угловой скоростью 16 рад/сек. Определить, сколько оборотов сделает колесо за 5 мин вращения.

Решение 1.

1.    Находим угол поворота маховика в радианах, имея в виду,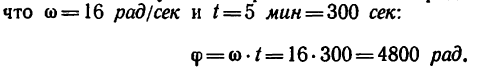
2.    Находим число оборотов маховика:

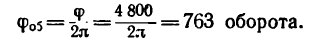
Таким образом, за 5 мин маховик сделает 763 оборота. Решение 2.

1.    Переведем угловую скорость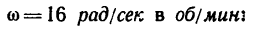

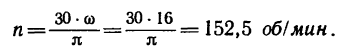
2.    Имея в виду, что уравнение равномерного вращательного движения можно представить так:

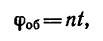
где 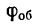- в оборотах; n —об/мин и t— в мин, находим число оборотов маховика:

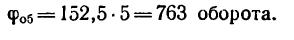
Задача №2

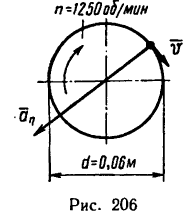
Вал, диаметр которого 0,06 м, вращается равномерно и делает 1200 об/мин. Определить скорость и ускорение точек вала на его поверхности (рис 206). Решение.

1.    Скорость точки вращающегося тела можно найти по формуле

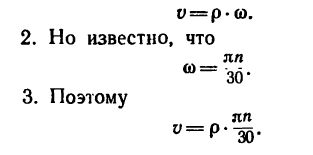
4 Подставим сюда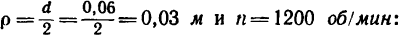

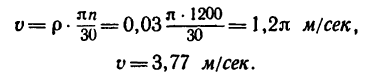
Вал вращается равномерно, значит скорость точек остается

численно неизменной. По этой же касательное ускорение.

5. Нормальное ускорение найдем из формулы

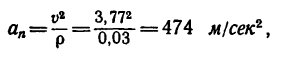
которое также в данном случае остается по модулю неизменным.

Задача №3

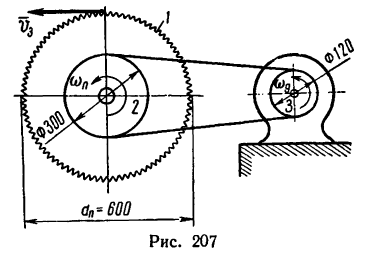
Дисковая пила 1 имеет диаметр 600 мм.

На валу пилы насажен шкив 2 диаметром 300 мм, а шкив

соединен бесконечным ремнем со шкивом двигателя 3 (рис. 207) дна» метром 120 мм. С какой угловой скоростью должен вращаться шкив двигателя, чтобы скорость зубьев пилы не превышала 15 м/сек?

Решение.

1.    Так как пила 1 и шкив 2 насажены на одном валу, то они имеют одну и ту же угловую скорость <о„ и скорость зубьев пилы 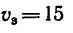м/сек зависит от 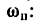потому что

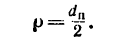
2.    Находим угловую скорость шкива 2, который обеспечивает необходимую рабочую скорость зубьев пилы:

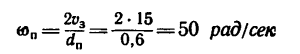
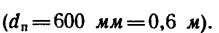
3.    Теперь найдем угловую скорость юд шкива двигателя. Шкивы 2 и 3 соединены бесконечным ремнем. Полагая, что

ремень не растягивается и не проскальзывает на шкивах, можно считать, что все его точки движутся с одной и той же скоростью Ор. Это означает, что скорости точек, расположенных на поверхностях обоих шкивов, одинаковы и равны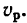

Поэтому применим зависимость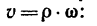
Отсюда

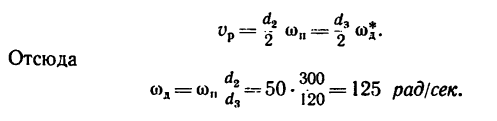
4.    Если перевести эту угловую скорость в об[мин, то

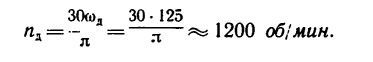
Таким образом, для того чтобы зубья пилы имели скорость 15 м/сек, шкив двигателя должен вращаться с угловой скоростью 125 рад/сек или 1200 об/мин.