
Равномерное прямолинейное движение точки в теоретической механике
Кинематика точки:
В этой главе в основном рассмотрены методы решения задач, в которых закон движения точки выражен так называемым естественным способом: уравнением s=f(t) по заданной траектории *.
В этом случае главными параметрами, характеризующими движение точки но заданной траектории, являются: s— расстояние от заданного начального положения и t—время.
Величина, характеризующая в каждый данный момент времени направление и быстроту движения точки, называется скоростью
* Решения задач, в которых закон движения задан координатным способом, рассмотрены в конце главы.
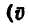
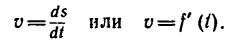
Ускорение 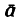 точки в каждый данный момент времени характеризует быстроту изменения скорости. При этом нужно отчетливо понимать, что скорость — вектор, и, следовательно, изменение скорости может происходить по двум признакам: по числовой величине (по модулю) и по направлению.
точки в каждый данный момент времени характеризует быстроту изменения скорости. При этом нужно отчетливо понимать, что скорость — вектор, и, следовательно, изменение скорости может происходить по двум признакам: по числовой величине (по модулю) и по направлению.
Быстрота изменения модуля скорости характеризуется касательным ускорением 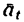 — составляющей полного ускорения
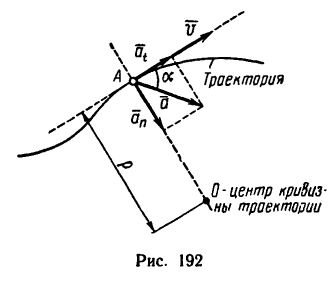
— составляющей полного ускорения 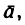 направленной по касательной к траектории (см. рис. 192).
направленной по касательной к траектории (см. рис. 192).
Числовое значение касательного ускорения в общем случае определяется по формуле
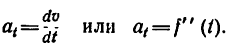
Быстрота изменения направления скорости характеризуется нормальным (центростремительным) ускорением 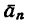 - составляющей полного ускорения
- составляющей полного ускорения 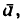 направленного по нормали к траектории в сторону центра кривизны (см. рис. 192).
направленного по нормали к траектории в сторону центра кривизны (см. рис. 192).
Числовое значение нормального ускорения определяется в общем случае по формуле
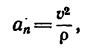
где v—модуль скорости точки в данный момент;
р— радиус кривизны траектории в месте, где находится точка в данный момент.
После того как определены касательное и нормальное ускорения, легко определить и ускорение 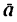 (полное ускорение точки).
(полное ускорение точки).
Так как касательная и нормаль взаимно перпендикулярны, то числовое значение ускорения 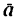 можно определить при помощи
можно определить при помощи
теоремы Пифагора:
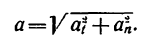
Направление 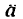 можно определить, исходя из тригонометрических соотношений, по одной из следующих формул:
можно определить, исходя из тригонометрических соотношений, по одной из следующих формул:
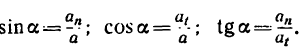
Но можно сначала определить направление полного ускорения й, использовав формулу
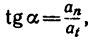
а затем найти числовое значение а:
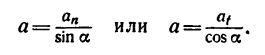
Касательное и нормальное ускорения точки являются главными кинематическими величинами, определяющими вид и особенности движения точки.
Наличие касательного ускорения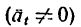 или его отсутствие
или его отсутствие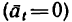 определяют соответственно неравномерность или равномерность движения точки.
определяют соответственно неравномерность или равномерность движения точки.
Наличие нормального ускорения 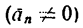 или его отсутствие
или его отсутствие 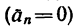 определяют криволинейность или прямолинейность движения точки.
определяют криволинейность или прямолинейность движения точки.
Движение точки можно классифицировать так:
- а) равномерное прямолинейное
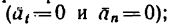
- б) равномерное криволинейное
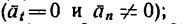
- в) неравномерное прямолинейное
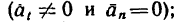
- г) неравномерное криволинейное
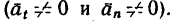
Таким образом, движение точки классифицируется по двум признакам: по степени неравномерности движения и по виду траектории.
Степень неравномерности движения точки задана уравнением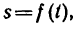 а вид траектории задается непосредственно.
а вид траектории задается непосредственно.
Равномерное прямолинейное движение точки
Если 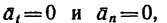 то вектор скорости остается постоянным (S = const), т. е. не изменяется ни. по модулю, ни по направлению. Такое движение называется равномерным прямолинейным.
то вектор скорости остается постоянным (S = const), т. е. не изменяется ни. по модулю, ни по направлению. Такое движение называется равномерным прямолинейным.
Уравнение равномерного движения имеет вид

или в частном случае, когда начальное расстояние 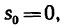

В уравнение (a) входит всего четыре величины, из них две переменные: s и t и две постоянные:  Поэтому в условии задачи на равномерное и прямолинейное движение точки должны быть заданы три любые величины.
Поэтому в условии задачи на равномерное и прямолинейное движение точки должны быть заданы три любые величины.
При решении задач необходимо выяснить все заданные величины и привести их к одной системе единиц. При этом нужно заметить, что как в системе МКГСС (технической), так и в СИ единицы всех кинематических величин одинаковы:
расстояние s измеряется в м, время t — в сек, скорость  -в м/сек.
-в м/сек.
Задача №1
Точка, совершая равномерное и прямолинейное движение, проходит прямолинейный участок траектории АВ, равный 60 м (рис. 193, а) за 30 сек. Простояв затем 10 сек на месте,
точка возвращается в исходное положение со скоростью 3 м/сек. Сколько всего времени проходит от начала движения точки до ее возвращения в исходное положение? Какой путь проходит точка?
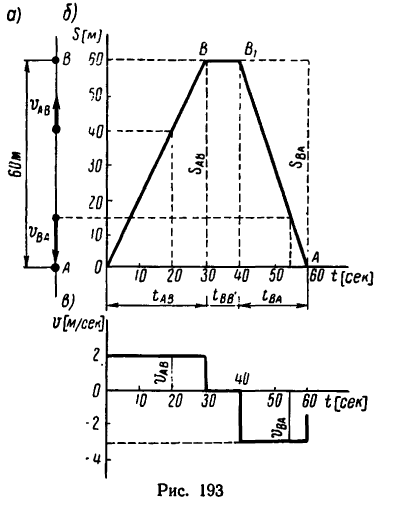
Построить графики перемещения и скорости точки.
Решение.
1. Расстояние от А до В, равное 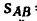 = 60 м, равномерно пройдено за
= 60 м, равномерно пройдено за 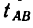 = = 30 сек. В данном случае начальное расстояние
= = 30 сек. В данном случае начальное расстояние 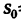 = 0, поэтому из уравнения (б) находим скорость точки на участке АВ
= 0, поэтому из уравнения (б) находим скорость точки на участке АВ
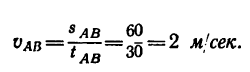
2. Точка находится в покое в течение времени 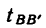 = Ю сек.
= Ю сек.
3. Точка возвращается в исходное положение, пройдя расстояние от В до A 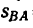 = 60 м со скоростью
= 60 м со скоростью 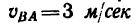 за время
за время
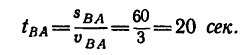
4. Время от начала движения до момента возвращения в исходное положение равно:
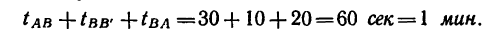
5. Путь, пройденный точкой за это время, 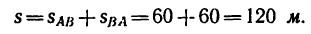
6. Построим теперь график перемещения (рис. 193,в) и скорости точки (рис. 193, в) с одинаковым масштабом по оси времени.
Задача №2
Из двух пунктов А и В прямолинейного шоссе, находящихся один от другого на расстоянии 100 км, одновременно выезжают навстречу друг другу два велосипедиста и двигаются с постоянными скоростями. Велосипедист, выезжающий из А, имеет скорость 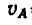 = 40 км/ч, а велосипедист, выезжающий из В, —
= 40 км/ч, а велосипедист, выезжающий из В, —
скорость 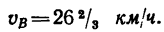 Определить, за какое время каждый из них проедет расстояние 100 км. Через сколько часов и где они встретятся?
Определить, за какое время каждый из них проедет расстояние 100 км. Через сколько часов и где они встретятся?
Решение.
1. Находим время, затраченное первым велосипедистом на проезд от точки А до В:
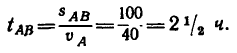
2. Находим время, затраченное вторым велосипедистом на проезд от точки В до А:
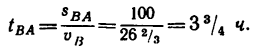
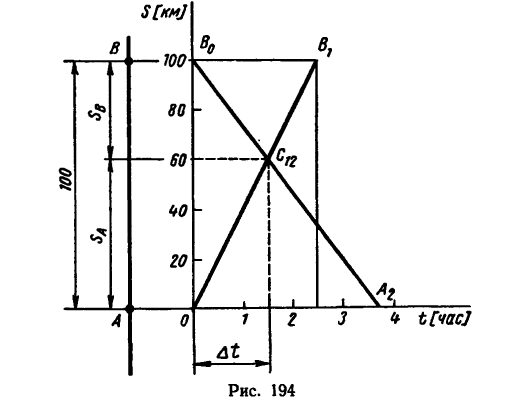
3. Время и место встречи велосипедистов наиболее просто определить графически. Расстояние между пунктами А и В, равное 100 км, изобразим на оси ординат отрезком в 50 мм (рис. 194),
т. е. в масштабе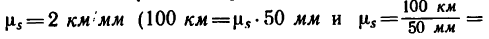
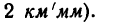
По оси абсцисс отложим время в масштабе 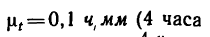
изображены отрезком 40 мм, поэтому 4 ч=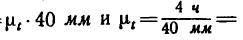
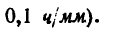
Первый велосипедист расстояние от А до В проезжает за 2,5 ч. Нго перемещение изображается на графике прямой 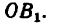
Второй велосипедист расстояние от В до А проезжает за 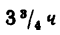 и его перемещение изображается на графике прямой
и его перемещение изображается на графике прямой 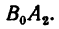
Точка 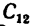 пересечения обоих графиков указывает место и время встречи. Встреча происходит на расстоянии
пересечения обоих графиков указывает место и время встречи. Встреча происходит на расстоянии 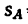 = 60 км от пункта А (или на расстоянии
= 60 км от пункта А (или на расстоянии 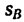 = 40 км от пункта В) через
= 40 км от пункта В) через 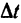 = 1,5 ч после начала движения велосипедистов.
= 1,5 ч после начала движения велосипедистов.
Если вместо графического решения применить аналитическое, то нужно рассуждать таким образом.
Допустим, что место встречи происходит на расстоянии s от пункта А, а время встречи 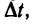 считая от начала движения. Тогда уравнение движения первого велосипедиста примет вид
считая от начала движения. Тогда уравнение движения первого велосипедиста примет вид

и уравнение движения второго велосипедиста

где 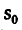 =100 км — расстояние второго велосипедиста от пункта А в момент начала отсчета (при t = 0).
=100 км — расстояние второго велосипедиста от пункта А в момент начала отсчета (при t = 0).
Так как левые части уравнения (1) и (2) равны, то
Отсюда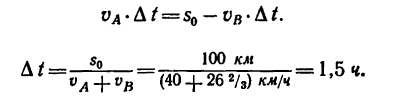
Из уравнения (1) определяем s:
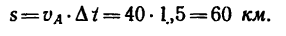
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Равномерное криволинейное движение точки
- Равнопеременное движение точки
- Неравномерное движение точки по любой траектории
- Определение траектории, скорости и ускорения точки
- Равновесие трех непараллельных сил
- Сочлененные системы
- Равновесие пространственной системы сходящихся сил
- Определение положения центра тяжести тела