Равномерное криволинейное движение точки в теоретической механике

Равномерное криволинейное движение точки:

Если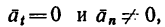

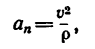
В частном случае движения точки по окружности (или по дуге окружности) радиус кривизны траектории во всех ее точках постоянный:

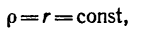
а так как и числовое значение скорости постоянно, то

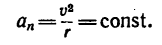
При равномерном движении числовое значение скорости определяется из формулы

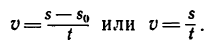
Если точка совершит полный пробег по окружности, то путь s равен длине окружности, т. е. 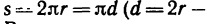диаметр), а время равно периоду, т. е. t=T. Выражение-скорости примет вид

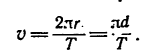
Задача №1

Тепловоз проходит закругление длиной 800 м за 50 сек. Радиус закругления по всей его длине постоянный и равняется 400 м. Определить скорость тепловоза и нормальное ускорение, считая движение равномерным.

Решение.

1.    Принимая тепловоз за материальную точку, найдем его скорость:

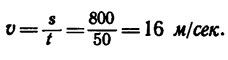
2.    Находим нормальное ускорение:

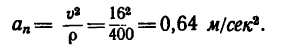
3.    Таким образом, при равномерном движении тепловоза по закруглению со скоростьюон имеет нормальное ускорение (рис. 195).

Задача №2

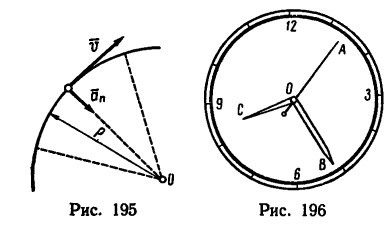
Определить, с какими скоростями движутся точки А, В и С, расположенные на концах секундной, минутной и часовой стрелок часов. Принять длину секундной и минутной стрелок равной 14 мм и длину часовой стрелки — 10 мм (рис. 196).

Решение.

1.    Скорости данных точек найдем из формулы

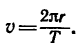
2.    Определим исходные данные.

Для точки А (конец секундной стрелки)

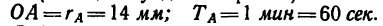
Для точки В (конец минутной стрелки)

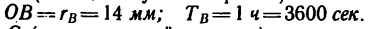
Для точки С (конец часовой стрелки)

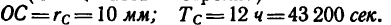
3.    Находим искомые скорости:

Следующие три задачи рекомендуется решить самостоятельно.