
Равномерное и неравномерное движение в физике - виды, формулы и определения с примерами
Содержание:
Равномерное движение:
Если тело за первую секунду прошло путь 5 м, за вторую — снова 5 м, за третью — 5 м и т. д., т. е. за каждую любую секунду тело проходит одинаковый путь, то такое движение является равномерным.
Опыт. Возьмём стеклянную трубку длиной 1 м и диаметром 1 см (рис. 4). Закроем её с обеих сторон пробками, предварительно налив в неё воды так, чтобы в ней остался воздушный пузырёк. Теперь установим трубку вертикально или с наклоном так, чтобы в начальный момент воздушный пузырёк был расположен в нижнем конце трубки. Пузырёк начнёт медленно всплывать, и будет удобно наблюдать за характером его движения. В результате опыта убеждаемся, что пузырёк воздуха будет проходить одинаковые отрезки пути за одинаковые интервалы времени. Итак, движение пузырька является равномерным.
Равномерным движением называют такое движение, при котором тело за любые одинаковые интервалы времени проходит одинаковый путь.
Примером равномерного движения является движение точки земной поверхности при обращении Земли вокруг своей оси. Равномерным можно считать движение точек часовых стрелок, равномерно может двигаться автомобиль по прямой и ровной дороге.
Большинство движений в природе являются неравномерными. Например, автобус, отходя от остановки, за одинаковые интервалы времени проходит всё больший путь, а приближаясь к остановке, - наоборот. Бегун, принимая участие в соревнованиях, затрачивает на прохождение одинаковых кругов разное время. Движение автобуса и бегуна — это примеры неравномерного движения.
При неравномерном движении тело за одинаковые интервалы времени проходит неодинаковый путь.
Скорость движения и единицы скорости
Лодку, равномерно движущуюся по поверхности моря, обгоняют дельфины, плывущие также равномерно. Чем различаются эти равномерные движения: лодки и дельфинов? Их отличие состоит в том, что дельфины движутся быстрее лодки. Самолёт движется быстрее поезда, но медленнее, чем искусственный спутник Земли. А это означает, что на протяжении одинакового интервала времени дельфины проплывают больший путь, чем лодка, самолёт пролетает больший путь, чем проходит поезд, а спутник — больший путь, чем самолёт.
Движения лодки, дельфинов, поезда, самолета и спутника различаются их скоростью. Говорят, что то тело, которое за единицу времени проходит больший путь, движется с большей скоростью.
Скорость равномерного движения тела - это физическая величина, которая показывает, какой путь проходит тело за единицу времени.
Например, если за каждый час автомобиль проезжает 60 км, а самолет пролетает 600 км, то говорят, что скорость движения автомобиля равняется 60 км в час, а скорость движения самолёта — 600 км в час.
Скорость движения тела обозначают малой латинской буквой 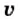
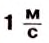 - это скорость движения тела, при котором оно за 1 с проходит путь 1 м.
- это скорость движения тела, при котором оно за 1 с проходит путь 1 м.
Применяют ещё такие единицы скорости движения тела:
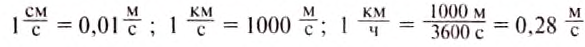
Чтобы определить скорость равномерного движения тела, нужно путь, пройденный телом за определённый интервал времени, разделить на этот интервал: 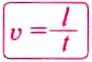
где 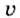 — скорость движения тела;
— скорость движения тела;
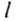 - путь, пройденный телом;
- путь, пройденный телом;
t — время движения тела.
В отличие от других физических величин значения скоростей лежат в определённых пределах: от 0 (когда тело находится в покое) до скорости распространения света в безвоздушном пространстве, которая равна 300 000 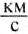 .
.
Скорость обычной ходьбы человека равна 1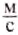 . Во время бега на длинные дистанции спортсмен развивает скорость до 7
. Во время бега на длинные дистанции спортсмен развивает скорость до 7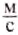 , а на короткие — до 10
, а на короткие — до 10 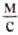 . Велосипедист может ехать со скоростью 14
. Велосипедист может ехать со скоростью 14 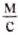 . В воде пловец движется со скоростью 2
. В воде пловец движется со скоростью 2 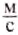 .
.
Эти значения скоростей незначительны по сравнению со скоростью представителей животного мира. Если бы ноги спортсмена-бегуна двигались так же быстро, как ноги муравья, то он развил бы скорость до 1500 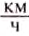 . Наибольшая скорость движения человека втрое меньше скорости движения гепарда. В воде человек плавает в 18 раз медленнее, чем самый быстроходный житель океана - меч-рыба. Голубой кит, масса которого равна 130 т, может развивать в воде скорость до 37
. Наибольшая скорость движения человека втрое меньше скорости движения гепарда. В воде человек плавает в 18 раз медленнее, чем самый быстроходный житель океана - меч-рыба. Голубой кит, масса которого равна 130 т, может развивать в воде скорость до 37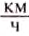 . Для сравнения укажем, что моторная лодка может двигаться со скоростью 30
. Для сравнения укажем, что моторная лодка может двигаться со скоростью 30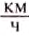 .
.
Однако человек создал транспортные средства, развивающие значительные скорости. Гепард уже не может соревноваться с легковым автомобилем, поездом или мотоциклом. Специальные гоночные автомобили развивают скорость до
284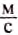 (1022,4
(1022,4 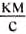 ). Вертолёты и самолёты значительно опережают золотистого орла — самую быструю из птиц. Космическим ракетам, летящим к другим планетам, сообщают скорости от 10 до 17
). Вертолёты и самолёты значительно опережают золотистого орла — самую быструю из птиц. Космическим ракетам, летящим к другим планетам, сообщают скорости от 10 до 17 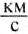 .
.
Скорость движения тела характеризуется не только числовым значением, но и направлением. Например, чтобы узнать, где будет находиться через 5 ч путешествия турист, вышедший из Киева, нужно знать не только с какой скоростью он движется, а и в каком направлении (направление скорости).
Величины, зависящие от направления в пространстве, называют векторными величинами, или векторами.
Скорость движения тела является векторной величиной.
На рисунках вектор скорости изображают стрелкой, направление которой совпадает с направлением скорости, а длина равна числовому значению скорости в определенном масштабе (рис. 5).
Зная скорость равномерного движения тела, можно определить путь, который оно проходит за определённое время. Пусть, например, велосипедист движется со скоростью 5 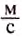 . Это означает, что за каждую секунду он проезжает 5 м. Поскольку движение велосипедиста равномерное, то за 10 с он преодолеет путь, в 10 раз больший, т. е. 5
. Это означает, что за каждую секунду он проезжает 5 м. Поскольку движение велосипедиста равномерное, то за 10 с он преодолеет путь, в 10 раз больший, т. е. 5 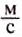 умножим на 10 с и получим 50 м.
умножим на 10 с и получим 50 м.
Чтобы определить путь, который тело проходит при равномерном движении, нужно скорость движения тела умножить на время его движения:
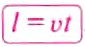
Зная путь и скорость равномерного движения тела, можем определить время его движения. Например, за какое время пловец переплывёт озеро шириною 200 м, если он движется со скоростью 2 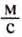 ?
?
За 1 с он проплывает 2 м. Чтобы определить, сколько секунд он затратит на то, чтобы проплыть 200 м, нужно узнать, сколько раз в 200 м содержится 2 м. Для этого 200 разделим на 2 и получим 100. Время, за которое пловец переплывёт озеро, равно 100 с, или 1 мин 40 с.
Чтобы определить время движения тела, нужно пройденный телом путь разделить на скорость движения тела:
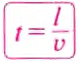
Это интересно знать:
Американская ящерица бегает по воде, как по твёрдой земле, со скоростью 11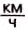 . Если бы это мог сделать человек, то его ступни размерами напоминали бы раскрытые зонтики, а за секунду он должен был бы делать 20 шагов.
. Если бы это мог сделать человек, то его ступни размерами напоминали бы раскрытые зонтики, а за секунду он должен был бы делать 20 шагов.
В Австралии каждый год проводятся соревнования, в которых принимают участие необычные бегуны - земляные червяки - самые быстрые безногие бегуны (ползуны), перемещающиеся со скоростью 15 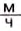 .
.
Средняя скорость неравномерного движения
Если тело движется неравномерно, то за одинаковые интервалы времени оно проходит неодинаковые пути. Из этого можем сделать вывод, что скорость движения тела за каждый интервал времени изменяется.
Значения скоростей движения в живой и неживой природе лежат в широком интервале, некоторые из них приведены в таблице 1.
Скорости движения в природе, 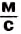 . Таблица 1
. Таблица 1

Не все указанные в табл. 1 движения являются равномерными. Лишь звук и свет при определённых условиях распространяются с постоянной скоростью. Скорости остальных тел изменяются во время движения. Поэтому для них указаны средние или максимально достижимые значения.
Во время неравномерного движения тела его скорость может значительно изменяться в разных точках траектории, но для упрощения часто пользуются средней скоростью неравномерного движения на определённом участке пути или за определённое время движения, условно полагая его равномерным.
Средняя скорость движения тела определяется отношением пройденного им пути к полному времени движения:
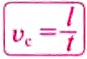
где 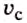 — средняя скорость движения тела;
— средняя скорость движения тела;
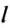 — весь пройденный телом путь;
— весь пройденный телом путь;
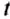 — полное время движения тела.
— полное время движения тела.
Конечно, полученные при этом значения средней скорости могут не совпадать со скоростью движения тела на отдельных участках траектории. При неравномерном движении тело на одних участках имеет меньшую скорость, на других — большую. Например, самолёт, начиная взлёт, увеличивает свою скорость, потом летит с определённой постоянной скоростью, перед посадкой уменьшает скорость движения.
Это интересно знать:
Если двигаться равномерно по прямой (скорость указана в скобках), то путешествие на Луну продолжалось бы:
- •пешком (5
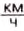 ) — 8 лет 280 дней;
) — 8 лет 280 дней; - •на велосипеде (30
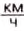 ) — 1 год 163 дня;
) — 1 год 163 дня; - •на автомобиле (100
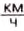 ) — 160 дней;
) — 160 дней; - •на космическом корабле (28 000 4
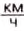 ) — 13 ч 43 мин.
) — 13 ч 43 мин.
Графическое изображение равномерного движения тела
Как известно, все тела природы находятся в механическом движении. Они могут двигаться равномерно или неравномерно по множеству разных траекторий, которые могут быть очень сложными. Далее будем рассматривать простейший для исследования и описания вид механического движения тел - прямолинейное равномерное движение.
Прямолинейное движение — это движение тела, траекторией которого является прямая линия. Примером прямолинейного движения может быть движение автомобиля на участке шоссе, где нет подъёмов, спусков и поворотов.
Прямолинейным равномерным движением называют такое движение, при котором тело за любые равные интервалы времени проходит одинаковые пути по прямолинейной траектории.
Прямолинейное равномерное движение тела очень удобно представлять и изучать в виде графиков зависимости пройденного телом пути от времени его движения (график движения) и зависимости скорости тела от времени его движения (график скорости).
Рассмотрим пример. Пусть автомобиль движется из Киева в Одессу со скоростью 100 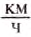 мотоциклист — со скоростью 50
мотоциклист — со скоростью 50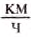 . Для того чтобы построить график зависимости пройденного автомобилем пути от времени движения, нужно воспользоваться формулой
. Для того чтобы построить график зависимости пройденного автомобилем пути от времени движения, нужно воспользоваться формулой 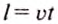 и составить такую таблицу.
и составить такую таблицу.
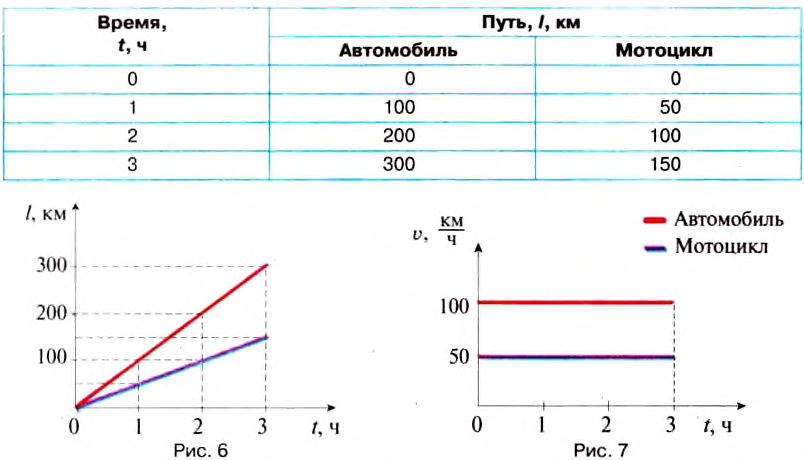
Далее на вертикальной оси откладываем в масштабе значения пути 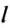 , а на горизонтальной оси - соответствующие им значения времени движения t, наносим точки на плоскость и строим графики движения (рис. 6).
, а на горизонтальной оси - соответствующие им значения времени движения t, наносим точки на плоскость и строим графики движения (рис. 6).
Как видно из рисунка, график зависимости пройденного телом пути от времени, или график движения, - это прямая линия, которая проходит через начало координат и направлена под углом к оси времени, причём угол наклона к оси времени тем меньший, чем меньше скорость движения тела. Скорость движения автомобиля больше скорости движения мотоциклиста, поэтому угол наклона графика движения автомобиля к оси времени больший.
Чтобы построить график зависимости скорости движения тела от времени движения, или график скорости, нужно на вертикальной оси отложить значения скорости 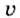 , а на горизонтальной оси — соответствующие значения времени движения t, нанести точки на плоскость и провести через них сплошную линию. Для автомобиля и мотоциклиста получим две прямые линии, параллельные оси времени (рис. 7). Это наглядно показывает, что равномерное движение является движением с постоянной (неизменной во времени), скоростью.
, а на горизонтальной оси — соответствующие значения времени движения t, нанести точки на плоскость и провести через них сплошную линию. Для автомобиля и мотоциклиста получим две прямые линии, параллельные оси времени (рис. 7). Это наглядно показывает, что равномерное движение является движением с постоянной (неизменной во времени), скоростью.
Теперь рассмотрим другой случай. Пусть велосипедист двигался 5 с
со скоростью 10 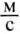 , а следующие 5 с — со скоростью 5
, а следующие 5 с — со скоростью 5 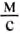 . Построим графики зависимости пройденного велосипедистом пути и скорости его движения от времени движения. Построение выполняем, как и в предыдущем примере, составив таблицу:
. Построим графики зависимости пройденного велосипедистом пути и скорости его движения от времени движения. Построение выполняем, как и в предыдущем примере, составив таблицу:

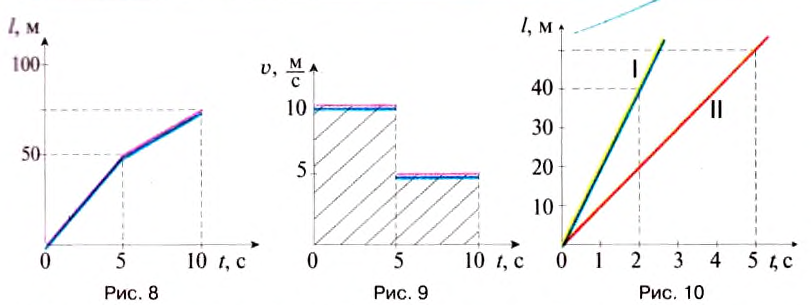
Из графика движения (рис. 8) видно, что на пятой секунде велосипедист уменьшил скорость движения, поэтому и наклон прямой уменьшился. Графиком такого движения является ломаная.
График зависимости скорости движения от времени (рис. 9) имеет вид ступенчатой линии — «ступеньки», которая образовалась также из-за уменьшения вдвое скорости движения велосипедиста на пятой секунде.
Рассмотрим заштрихованную фигуру под графиком скорости: она состоит из двух прямоугольников. Оказывается, что, определяя площадь этих прямоугольников как произведение их высоты и длины, мы умножаем скорость движения велосипедиста на время его движения и определяем пройденный им путь на обоих участках:
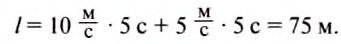
Из расчётов видно, что результат совпадает с данными в таблице.
Как видим, по графикам движения и скорости можно полностью определить вид, скорость, время и путь движения тела.
Рассматривая графики движения, приведённые на рисунке 10, делаем вывод, что это графики прямолинейного равномерного движения двух тел I и II, причём скорость тела I больше скорости тела II. По графику определяем, что скорость движения тела I равна 20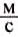 , а тела II -
, а тела II - 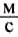 .
.
Пример №1
Если велосипедист за первые 5 мин проехал 5 км, а за следующие 10 мин — 10 км, то можно ли считать такое движение равномерным?
Ответ: да, так как велосипедист двигался с одинаковой скоростью — 1 .
.
Пример №2
Легковой автомобиль проходит расстояние 144 км за 2 ч. Определить скорость движения автомобиля, считая его движение равномерным.
Дано:
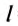 = 144 км
= 144 км
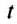 = 2ч
= 2ч
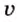 - ?
- ?
Решение:
Для расчета скорости движения автомобиля используем формулу:
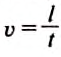 .
. 
Переведём километры в метры, а часы — в секунды.
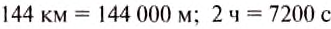 .
.
Тогда 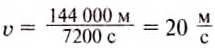
Ответ: скорость движения автомобиля равна 72 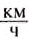 , или 20
, или 20 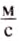 .
.
Неравномерное движение. Средняя и мгновенная скорость
Мы изучили равномерное прямолинейное движение. Однако реальные тела — люди, автомобили, корабли, самолеты и др. — чаще всего движутся и не прямолинейно, и не равномерно. Каковы закономерности таких движений?
Рассмотрим пример. По дорожке стадиона бежит легкоатлет, то увеличивая, то уменьшая скорость бега (рис. 59).
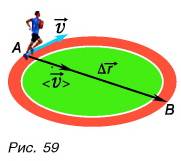
Движение легкоатлета и не прямолинейное, и не равномерное. Как описать такое движение? Из 7-го класса вам известно, что неравномерное движение характеризуют средней скоростью. Ее определяют как отношение пути к промежутку времени, за который этот путь пройден:

В нашем примере путь s — это длина дуги АВ, а 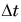 — промежуток времени, затраченный легкоатлетом на этот путь.
— промежуток времени, затраченный легкоатлетом на этот путь.
Более точно называть 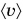 средней скоростью пути. Она показывает, какой путь в среднем проходило тело за единицу времени.
средней скоростью пути. Она показывает, какой путь в среднем проходило тело за единицу времени.
Средняя скорость пути ничего не говорит о направлении движения. Поэтому, кроме нее, вводят среднюю скорость перемещения, равную отношению перемещения 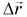 к промежутку времени
к промежутку времени 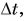 за которое перемещение произошло:
за которое перемещение произошло:

Из векторного равенства (2) следует, что средняя скорость перемещения 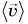 направлена так же, как перемещение
направлена так же, как перемещение 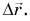 В нашем примере (см. рис. 59) вектор
В нашем примере (см. рис. 59) вектор 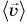 направлен по прямой АВ.
направлен по прямой АВ.
Каков смысл средней скорости перемещения 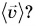 Она показывает, какое перемещение совершаю тело в среднем за единицу времени.
Она показывает, какое перемещение совершаю тело в среднем за единицу времени.
Сравнив формулу (2) с формулой 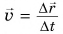 (§ 6) можно сказать, что средняя скорость перемещения
(§ 6) можно сказать, что средняя скорость перемещения 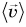 равна скорости такого равномерного прямолинейного движения, при котором за промежуток времени
равна скорости такого равномерного прямолинейного движения, при котором за промежуток времени 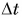 тело совершило бы перемещение
тело совершило бы перемещение 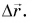
Средняя скорость пути 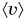 — величина скалярная, а средняя скорость перемещения
— величина скалярная, а средняя скорость перемещения 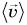 — векторная. Поэтому сравнивать среднюю скорость пути
— векторная. Поэтому сравнивать среднюю скорость пути 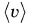 можно только с модулем средней скорости перемещения
можно только с модулем средней скорости перемещения 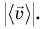 Мы знаем, что для одного и того же промежутка времени
Мы знаем, что для одного и того же промежутка времени 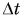 модуль перемещения
модуль перемещения 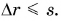 Значит, модуль средней скорости перемещения не больше средней скорости пути:
Значит, модуль средней скорости перемещения не больше средней скорости пути: 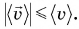
Средняя скорость характеризует движение за весь промежуток времени в целом. Она не дает информации о скорости движения в каждой точке траектории (в каждый момент времени). С этой целью вводится мгновенная скорость 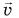 — скорость движения в данный момент времени (в данной точке траектории).
— скорость движения в данный момент времени (в данной точке траектории).
Как найти мгновенную скорость? Ее можно найти по формуле 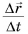 при условии, что промежуток времени
при условии, что промежуток времени 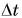 очень мал:
очень мал:

Обозначение 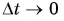 говорит о том, что скорость, найденная по формуле
говорит о том, что скорость, найденная по формуле 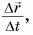 тем ближе к мгновенной скорости, чем меньше
тем ближе к мгновенной скорости, чем меньше 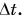
Как направлена мгновенная скорость 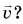 Она направлена по касательной к траектории в той точке, где в этот момент находится движущееся тело.
Она направлена по касательной к траектории в той точке, где в этот момент находится движущееся тело.

Понаблюдайте за раскаленными частицами, отрывающимися от точильного камня (рис. 60). Мгновенная скорость этих частиц в момент отрыва направлена по касательной к окружности, по которой они двигались до отрыва. Аналогично спортивный молот (рис. 61) начинает свой полет по касательной к той траектории, по которой он двигался при раскручивании метателем. Мгновенная скорость 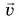 постоянна только при равномерном прямолинейном движении. Поясните почему.
постоянна только при равномерном прямолинейном движении. Поясните почему.
В дальнейшем мгновенную скорость будем называть просто скоростью.
Главные выводы:
- Быстрота неравномерного движения на участке траектории характеризуется средней скоростью, а в данной точке траектории — мгновенной скоростью.
- Мгновенная скорость приближенно равна средней скорости, определенной за малый промежуток времени. Чем меньше этот промежуток времени, тем ближе значение средней скорости к мгновенной.
- Мгновенная скорость направлена по касательной к траектории движения.
- При равномерном прямолинейном движении мгновенная скорость одинакова в любой точке траектории.
Пример №3
Первую половину прямолинейной дистанции лыжник двигался с постоянной скоростью 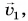 а вторую половину — с постоянной скоростью
а вторую половину — с постоянной скоростью 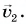 Определите среднюю скорость движения лыжника на всей дистанции, если
Определите среднюю скорость движения лыжника на всей дистанции, если 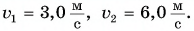

Решение
Сделаем рисунок к задаче (рис. 62):
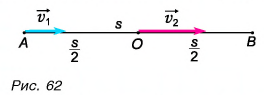
Поскольку лыжник двигался без изменения направления, его средняя скорость направлена так же, как скорости 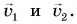 Модуль средней скорости
Модуль средней скорости 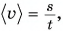 где s — длина дистанции,
где s — длина дистанции, 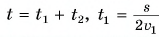 — время прохождения первой, a
— время прохождения первой, a 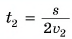 — второй половины дистанции. Найдем
— второй половины дистанции. Найдем 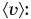

Ответ: 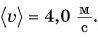
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |