
Рациональные неравенства и их системы с примерами решения
Содержание:
Простые рациональные неравенства и их системы
Рациональные неравенства одной переменной и методы их решения
Пусть А(х) и В(х) - рациональные выражения. Отношения вида 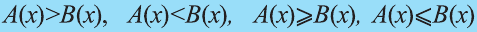
Пример:
Решите неравенство: 2(2х-5)(Зх-8)(5-4х)<0.
Решение:
Будем решать неравенство методом интервалов. С этим методом вы ознакомились в 9 классе. Приравняв выражения в скобках к нулю, получим
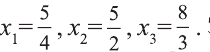
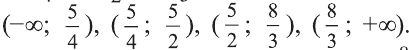 Выберем произвольное значение , например, х=10 из интервала
Выберем произвольное значение , например, х=10 из интервала  и, подставив в неравенство, заключаем, что на этом интервале наше неравенство верно. Значит, оно верно и на интервалах
и, подставив в неравенство, заключаем, что на этом интервале наше неравенство верно. Значит, оно верно и на интервалах 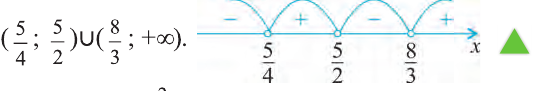
Пример:
Решите неравенство: 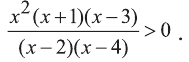
Решение:
Числа х = 2, х = 4 не удовлетворяют неравенству. При 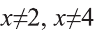 выполнено
выполнено 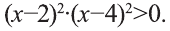 Поэтому при умножении обоих частей неравенства на
Поэтому при умножении обоих частей неравенства на
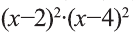 получим равносильное неравенство:
получим равносильное неравенство: 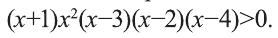
Приравняв выражения в скобках к нулю, Найдем 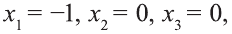
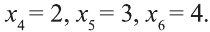 Эти числа разбивают числовую прямую на интервалы:
Эти числа разбивают числовую прямую на интервалы: 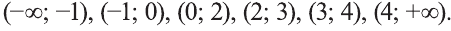 . Так как среди найденных чисел 0 встречается дважды, то на интервалах, граничащих с 0, знаки неравенства совпадают. Выбрав на последнем интервале число х= 10 и подставив его в наше неравенство, получим верное неравенство. Значит, наше неравенство имеет решение:
. Так как среди найденных чисел 0 встречается дважды, то на интервалах, граничащих с 0, знаки неравенства совпадают. Выбрав на последнем интервале число х= 10 и подставив его в наше неравенство, получим верное неравенство. Значит, наше неравенство имеет решение: 
Пример:
Решите неравенство: 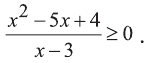
Решение:
Приравняем знаменатель, х-3 к нулю, а также, решив уравнение 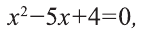 получим корни
получим корни 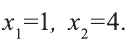 При этом числа
При этом числа 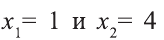 удовлетворяют неравенству. Значит, числовая прямая разбивается на следующие интервалы:
удовлетворяют неравенству. Значит, числовая прямая разбивается на следующие интервалы: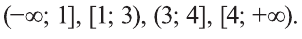
Взяв внутри последнего интервала значение х=5, получим верное
числовое неравенство. Поэтому решением нашего неравенства является
множество 
Системы простых рациональных неравенств
Пример:
Решите систему неравенств: 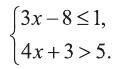
Решение:
Упрощая каждое неравенство системы, получим: 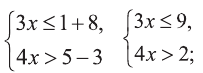
то есть 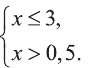 Значит, решение нашей системы есть множество (0,5; 3], являющееся общей частью интервалов
Значит, решение нашей системы есть множество (0,5; 3], являющееся общей частью интервалов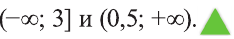
Пример:
Решите систему неравенств: 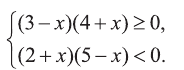
Решим каждое неравенство системы. Решением первого неравенства является интервал [-4; 3], а решением второго неравенства - множество 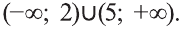 Решением нашей системы является общая часть этих множеств, то есть [-4; 2).
Решением нашей системы является общая часть этих множеств, то есть [-4; 2).
Простые иррациональные неравенства
Так как решения неравенств, как правило, представляют собой бесконечные числовые множества, то проверить их, подставляя некоторые значения неизвестной, не представляется возможным.
Одним из основных способов нахождения множества решений является способ преобразований, приводящих к равносильным неравенствам. Отметим, что возведение в нечетную степень обоих частей неравенства приводит к равносильному неравенству.
Если мы возводим обе части неравенства в четную степень, то нужно помнить, что мы получим равносильное неравенство лишь в случае, когда обе части исходного неравенства неотрицательны.
Неравенства, в которых неизвестное участвует под знаком корня называется иррациональным.
Для решения иррационального неравенства естественно привести его к равносильному путем возведения обоих его частей в соответствующую степень.
Рассмотрим простейшие иррациональные неравенства вида:
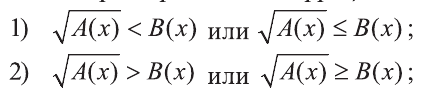
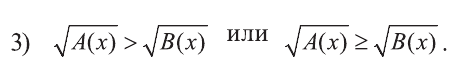
Иррациональное неравенство вида 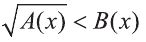 или аналогичное ему неравенство
или аналогичное ему неравенство 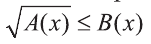 равносильны системе неравенств:
равносильны системе неравенств:
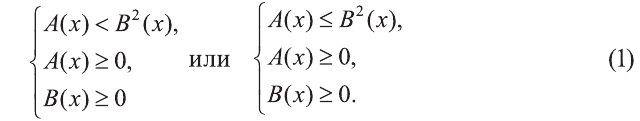
В системах (1) первое неравенство получилось путем возведения в соответствующую степень (в квадрат), второе неравенство представляет собой условие существования квадратного корня, а третье неравенство означает возможность возведения в квадрат.
Аналогично, для того, чтобы решить неравенство вида 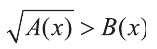 достаточно рассмотреть системы:
достаточно рассмотреть системы:
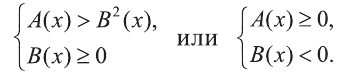
Иррациональное неравенство вида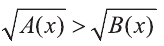 равносильно системе
равносильно системе
неравенств: 
Так как обе части неравенства для допустимых х принимают неотрицательные значения, то возведение в квадрат допустимо. В этом случае первое неравенство (3) получилось в результате возведения в квадрат, второе неравенство представляет собой условие существования квадратного корня. Очевидно, что условие выполняется автоматически.
Правила (1)—(3) считаются основными при решении иррациональных неравенств.
Рассмотрим несколько примеров.
Пример:
Решите неравенство: 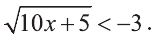
Решение:
Правая часть этого неравенства отрицательна, а левая принимает для всех допустимых значений х неотрицательные значения. Поэтому неравенство не имеет решений. Ответ: Решений не существует.
Пример:
Решите неравенство: 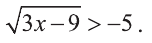
Решение:
Правая часть этого неравенства отрицательна, в то же время левая принимает для всех допустимых значений 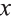 неотрицательные значения. Значит данное неравенство выполнено для всех, удовлетворяющих условию
неотрицательные значения. Значит данное неравенство выполнено для всех, удовлетворяющих условию 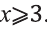
Ответ: 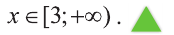
Пример:
Решите неравенство: 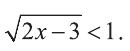
Решение:
Согласно правилу (1) 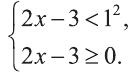
Так как, условие 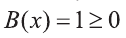 выполнено для всех х, его отдельно выписывать не обязательно.
выполнено для всех х, его отдельно выписывать не обязательно. 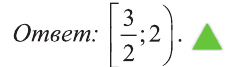
Пример:
Решите неравенство : 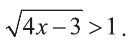
Решение:
Это неравенство решается по правилу (2). Так как, условие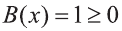 выполнено для всех х , то мы можем выписать непосредственно равносильное неравенство:
выполнено для всех х , то мы можем выписать непосредственно равносильное неравенство: 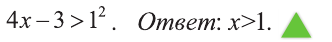
Пример:
Решите неравенство: 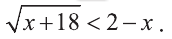
Решение:
Это неравенство решается по правилу (1):

Пример:
Решите неравенство: 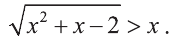
Решение:
Это неравенство решается по правилу (2): 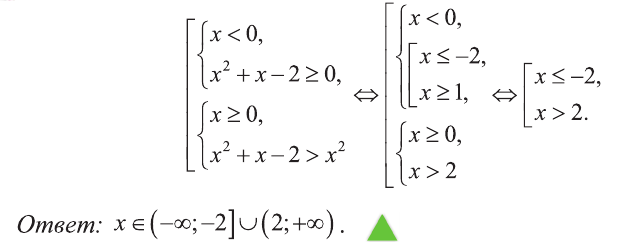
Пример:
Решите неравенство: 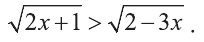
Решение:
Это неравенство решается по правилу (3):
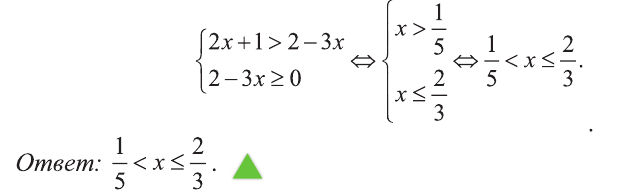
Пример:
Решите неравенство: 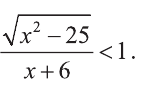
Решение:
Найдем множество допустимых значений х:
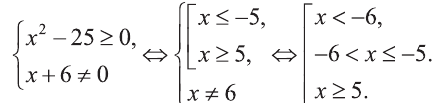
Если х + 6 > 0, то мы можем возвести обе части заданного неравенства в квадрат: 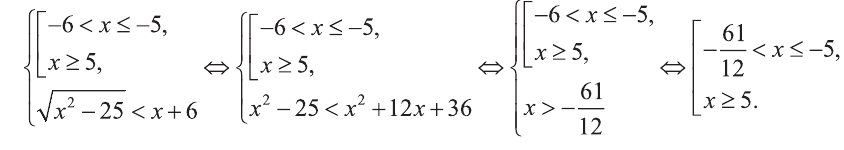 При
При 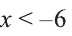 заданное неравенства обязательно выполняется:
заданное неравенства обязательно выполняется:
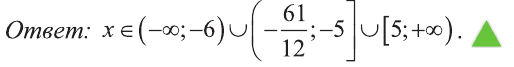
Замена переменной
Этот метод аналогичен соответствующему методу замены переменной, использованному при решении иррациональных уравнений.
Пример:
Решите неравенство: 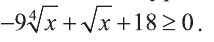
Решение:
Выпишем неравенство в виде: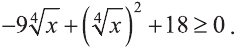
Введем новую переменную: 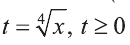 В этом случае
В этом случае
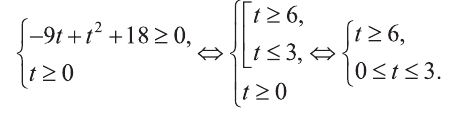
Значит: 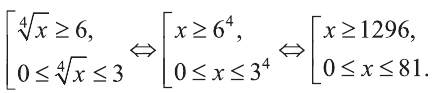
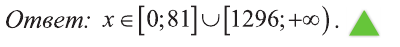
Пример:
Решите неравенство: 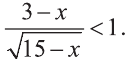
Решение:
Введем новую переменную: 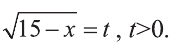
Отсюда, 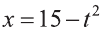 и получим рациональное неравенство от переменной t:
и получим рациональное неравенство от переменной t:
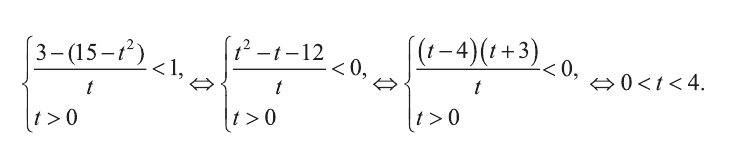
Из последнего неравенства найдем х:
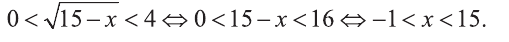
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |