Раскрытие неопределенностей - определение и вычисление с примерами решения

Раскрытие неопределенностей вида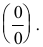

Пусть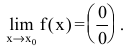

Если f(x) - рациональная дробь, то числитель и знаменатель дроби раскладывают на множители.

Пример №1

Вычислить предел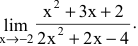

Решение:

Числитель и знаменатель дроби 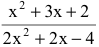при х=-2 обращаются в нуль. Имеем неопределенность вида 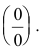Для ее раскрытия разложим числитель и знаменатель дроби на множители, а затем применим теоремы о пределах частного, суммы и произведения: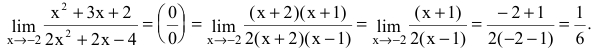

Если f(x) - дробь, содержащая иррациональные выражения, то выделение множителей вида 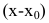достигается переводом иррациональностей в числитель или знаменатель.

Пример №2

Вычислить предел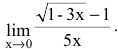

Решение:

Имеем неопределенность вида 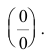Избавимся от иррациональности в числителе, умножив и разделив дробь на сопряженное к числителю выражение 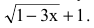Получим:

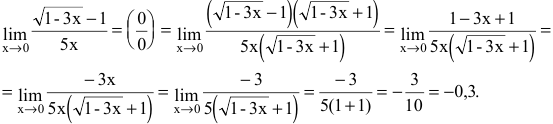
В остальных случаях для раскрытия неопределенности вида 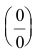используют первый замечательный предел или эквивалентные бесконечно малые функции.

Раскрытие неопределенностей вида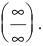

Пусть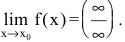

Если f(x) - рациональная дробь или дробь, содержащая иррациональности, то числитель и знаменатель делят на х в старшей степени.

Пример №3

Вычислить предел 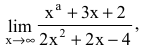если 1) а=2; 2) а=1; 3) а=4.

Решение:

Числитель и знаменатель дроби конечного предела не имеют. Имеем неопределенность вида 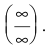Для ее раскрытия разделим числитель и знаменатель дроби на высшую степень х (в первом и втором случаях на 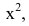во третьем - на 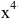), а затем воспользуемся теоремами о пределах функций: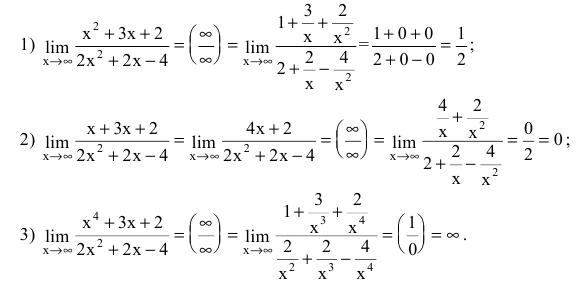

Вывод. Предел рациональной дроби на бесконечности равен отношению коэффициентов при старших степенях, если эти степени совпадают, нулю - если показатель степени числителя меньше показателя степени знаменателя и бесконечности в противном случае.

Замечание. Для раскрытия неопределенностей вида 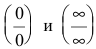используют также правило Лопиталя.

• Заказать решение задач по высшей математике

Раскрытие неопределенностей вида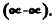

Неопределенное выражение вида 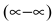преобразуется к неопределенности вида 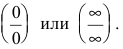Методику раскрытия такой неопределенности покажем на примерах.

Пример №4

Вычислить предел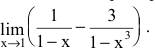

Решение:

Имеем неопределенность вида 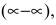которая преобразуется к неопределенности вида 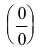приведением функции к общему знаменателю: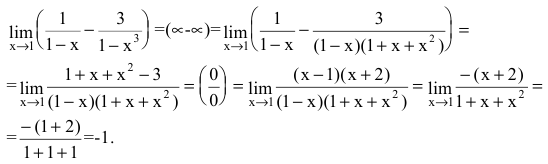

Пример №5

Вычислить предел последовательности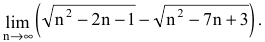

Решение:

Для раскрытия неопределенности вида 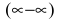умножим и разделим выражение в скобках на сопряженное:

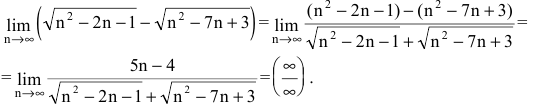
Получили неопределенность вида 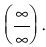Раскроем ее, разделив все члены полученного выражения на n:

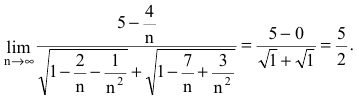
Раскрытие неопределенностей вида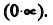

Неопределенное выражение вида 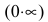получается при нахождении пределов вида 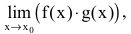где 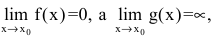и сводится к неопределенности вида  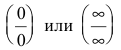следующим образом:

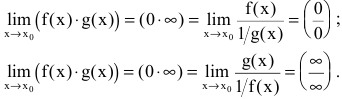
Замечание. При вычислении пределов показательно-степенных функций 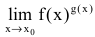могут получиться неопределенности вида 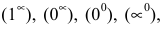для раскрытия которых используют второй замечательный предел или правило Лопиталя.