Расчет составной конструкции в теоретической механике

Расчет составной конструкции:

Постановка задачи. Плоская рама состоит из двух частей, соединенных одним шарниром. На раму действует момент и силы. Учитывая погонный вес, найти реакции опор.

План решения:

Составная конструкция, состоящая из двух тел, соединенных шарниром содержит четыре неизвестные реакции опор. Так как для одного тела под действием плоской системы сил можно составить только три независимых уравнения равновесия, то для определения реакций необходимо рассматривать равновесие каждой части составной конструкции в отдельности.

1-й  способ:

1. Разбиваем систему на два тела по сочленяющему шарниру. В месте разбиения прикладываем реакции отброшенной части. Внешние связи заменяем их реакциями.

2. Для каждого тела, образованного при разбиении, составляем по три уравнения равновесия.

3. Решаем систему шести уравнений. Определяем реакции опор.

4. Делаем проверку решения, составляя уравнения равновесия целой (нерасчлененной) системы.

2-й способ:

1. Разбиваем систему на два тела по сочленяющему шарниру. В месте разбиения прикладываем реакции отброшенной части. Внешние связи заменяем их реакциями.

2. Для каждого тела, образованного при разбиении, составляем уравнения моментов относительно точки сочленения. Полученные уравнения дополняем двумя уравнениями равновесия для всей конструкции в целом.

3. Решаем систему четырех уравнений. Определяем реакции опор.

4. Делаем проверку решения, составляя уравнения равновесия целой (нерасчлененной) системы.

Задача №1

Плоская рама состоит из двух частей, соединенных в точке С шарниром. На раму действует момент М = 100 кНм, горизонтальная сила Р = 20 кН и наклонная сила Q = 10 кН. Учитывая погонный вес р = 4 кН/м, найти реакции опор (рис. 40). Дано: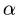

2.4. Расчет составной конструкции

Решение

1-й способ

1. Разбиваем конструкцию на два тела по сочленяющему шарниру С. Получаем две части (рис. 41-42). Внешние связи конструкции заменяем реакциями.

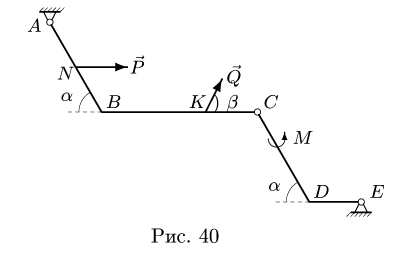
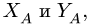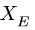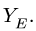В точке А прикладываем реакции в точке Е — реакции и К каждому телу в точке С прикладываем реакции отброшенной части. Согласно 3-му закону Ньютона, реакции 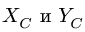для разных частей равны по величине и направлены в противоположные стороны.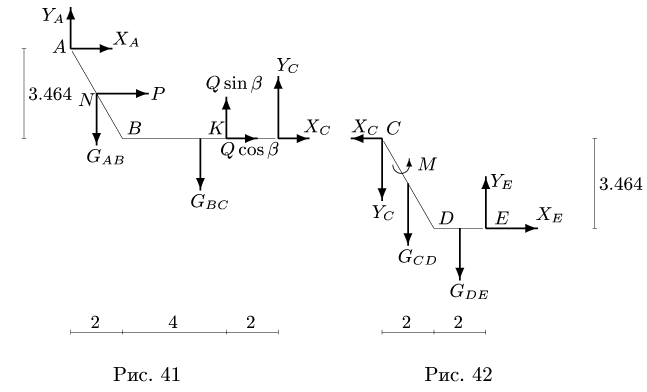

Система уравнений равновесия двух тел, образованных при разбиении, замыкается — имеем шесть уравнений равновесия (по три уравнения на каждую часть) и шесть неизвестных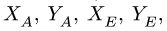

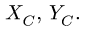
2. Для каждой отдельной части составляем по три уравнения равновесия:

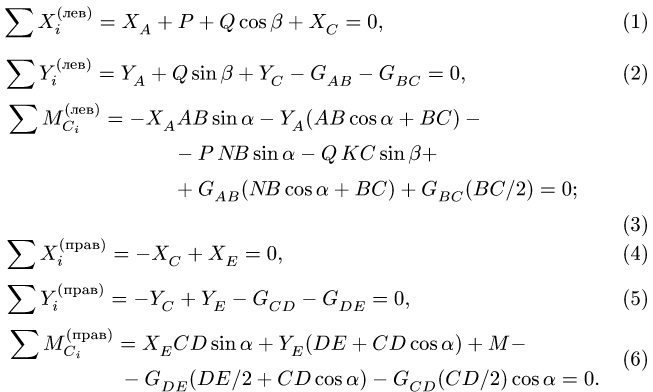
3. Решаем систему (1-6) относительно неизвестных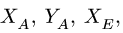 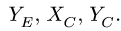Можно использовать любой способ решения системы линейных уравнений  Рекомендуем наиболее эффективный для таких систем метод исключения Гаусса.

Если для решения использовать компьютер, систему лучше записать в матричном виде, предварительно вычислив правые части системы (1-6) и коэффициенты при неизвестных. Величины сил тяжести участков вычисляем через погонный вес 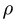по формуле 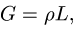где L — длина соответствующего участка. В нашем случае

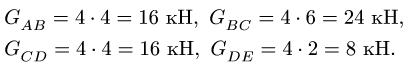
Система (1-6) имеет следующий матричный вид:

2.4.Расчет составной конструкции

Результаты расчетов в кН заносим в таблицу:
 

4. Делаем проверку решения, составляя уравнения равновесия для целой (нерасчлененной) системы (рис. 43):

2-й способ:

1. Разбиваем конструкцию на два тела по сочленяющему шарниру С. Получаем две части (рис. 41-42). Внешние связи конструкции заменяем реакциями.

2. Относительно шарнира С для каждой части конструкции составляем уравнения моментов (3) и (6). Для всей системы в целом составляем уравнения моментов (7,8) относительно опор А и Е.

3. Решаем систему четырех уравнений (3,6,7,8) относительно четырех неизвестных, замечая, что система распадается на две: уравнения (3) и (7) для 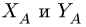и уравнения (6) и (8) для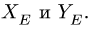

4. Делаем проверку решения, составляя уравнения равновесия целой (нерасчлененной) системы (рис. 43):

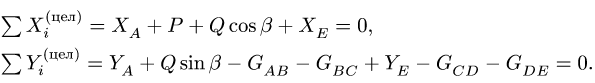
2.5. Конструкция с распределенными нагрузками

Конструкция с распределенными нагрузками

постановка задачи. Найти реакции опор плоской составной рамы, находящейся под действием линейно распределенной нагрузки и нагрузки, равномерно распределенной по дуге окружности.

План решения:

1. Внешние связи заменяем реакциями. Разбиваем систему на два тела по сочленяющему шарниру. К каждой из образовавшихся частей прикладываем реакции шарнира, помня о том, что части взаимодействуют с силами равными по величине и противоположными по направлению.

2. Линейную нагрузку с максимальным значением 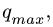распределенную по треугольнику, заменяем на сосредоточенную 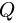в центре тяжести треугольника (1/3 длины участка L нагрузки, считая от прямого угла). Значение нагрузки вычисляем по формуле площади треугольника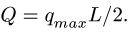

3. Нагрузку q, равномерно распределенную по дуге окружности радиусом R с центральным углом 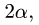заменим ее равнодействующей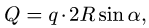направленной по биссектрисе центрального угла ([19], §21).

4. Для каждого тела составляем по три уравнения равновесия.

5. Решаем систему шести уравнений. Определяем реакции опор.

6. Делаем проверку решения, составляя уравнения равновесия для целой (нерасчлененной) системы.

Задача №2

Найти реакции опор плоской составной рамы, находящейся под действием линейно распределенной нагрузки с максимальной интенсивностью 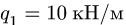на вертикальном участке рамы АВ

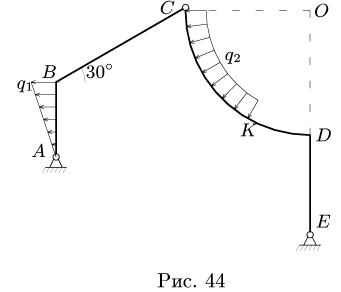
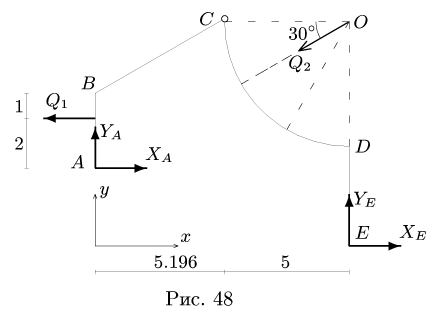
и нагрузки с интенсивностью 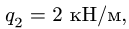равномерно распределенной по дуге СК окружности с центром в точке О (рис. 44). АВ = 3 м, ВС = 6 м, DE = 4 м, R = 5 м,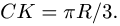

Решение

1. Внешние связи заменяем реакциями 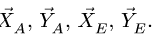Число неизвестных реакций больше трех. Следовательно, для решения задачи необходимо разбить конструкцию на две и рассмотреть равновесие каждой образовавшейся части(рис.45-46)

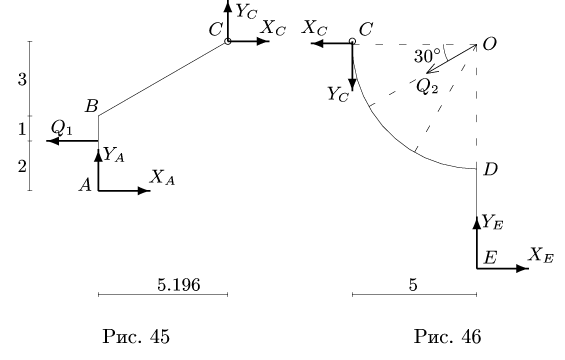
При разбиении по шарниру к каждой из частей прикладываем реакции шарнира, помня о том, что части взаимодействуют с силами, равными по величине и противоположными по направлению.

2. Нагрузку, распределенную по линейному закону, заменяем сосредоточенной 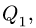приложенной к раме на расстоянии АВ/3 от максимального значения 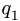в том же направлении (рис. 45). Величина равнодействующей 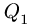вычисляется по формуле площади прямоугольного треугольника с катетами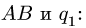

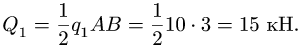
3. Нагрузку с интенсивностью 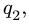равномерно распределенную по дуге СК, заменяем ее равнодействующей

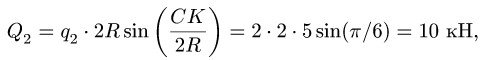
направленной по биссектрисе угла 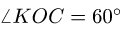(рис. 47). Так как 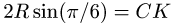, то величина 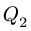совпадает со значением равнодействующей нагрузки, равномерно распределенной по хорде СК, той же интенсивности 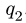. Воспользуемся тем, что вектор силы в теоретической механике является скользящим. Для удобства вычисления  момента силы 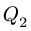переносим точку ее приложения вдоль линии действия силы в центр окружности О. То, что точка О не принадлежит раме, и сила как-бы "зависает" в воздухе, не должно смущать. Твердое тело CDE можно мысленно расширить до точки О, давая, таким образом, силе 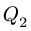реальную точку приложения.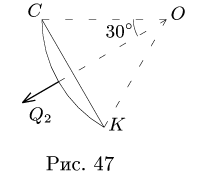

4. Составляем уравнения равновесия частей рамы:

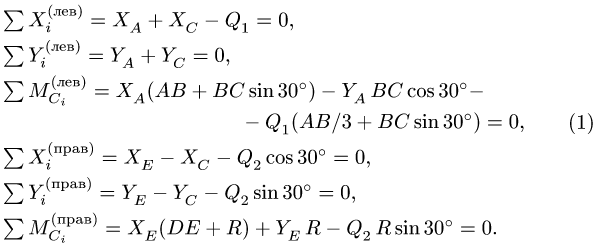
5. Решаем систему (1) шести уравнений с шестью неизвестными. Результаты расчетов в кН заносим в таблицу:

Гл.2.Произвольная плоская система сил

6. Выполняем проверку решения — составляем уравнения моментов для всей системы в целом (рис. 48):

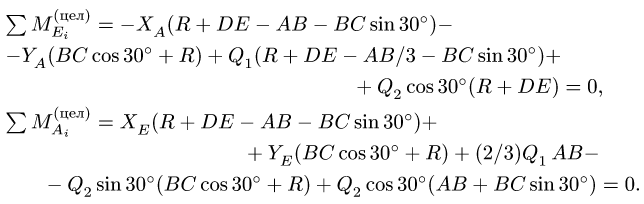
Замечание. Можно предложить второй способ решения задачи, рассмотренный в предыдущем параграфе (с. 54). Для каждого тела, образованного при разбиении, составляем уравнения моментов относительно точки сочленения С. Полученные уравнения дополняем двумя уравнениями равновесия для всей конструкции в целом (рис. 48).

Для данного примера это уравнения моментов относительно опорных шарниров А и Е.

Расчет системы трех тел, соединенных шарниром

Постановка задачи. Определить реакции опор конструкции, состоящей из трех тел, соединенных в одной точке шарниром.

План решения:

1. Расчленяем конструкцию на три отдельных тела и сочленяющий шарнир в качестве четвертого тела. Считая, что каждое из трех тел в точке сочленения взаимодействует только с осью шарнира, действие оси шарнира на тело заменяем ее реакциями.

2. Записываем по три уравнения равновесия для каждого из тел и два уравнения равновесия в проекциях для системы сил, приложенных к оси шарнира.

3. Решаем систему 11 уравнений с 11 неизвестными.

4. Выполняем проверку решения, составляя дополнительное уравнение равновесия для нерасчлененной конструкции.

Задача №3

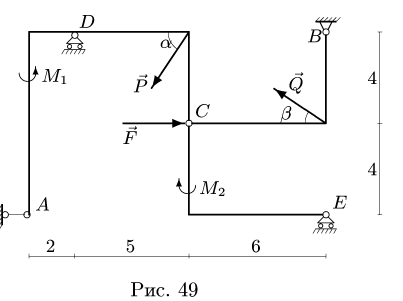
Определить реакции опор конструкции, состоящей из трех тел, соединенных в точке С шарниром. В точке В конструкция опирается на неподвижный шарнир, в точках D и Е — подвижные шарниры, в точке А — горизонтальный опорный стержень. На конструкцию действуют силы F — 40 кН, Р — 20 кН, Q — 10 кН и сосредоточенные моменты 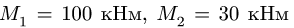(рис. 49); 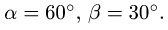Размеры на рисунке указаны в метрах.

Решение

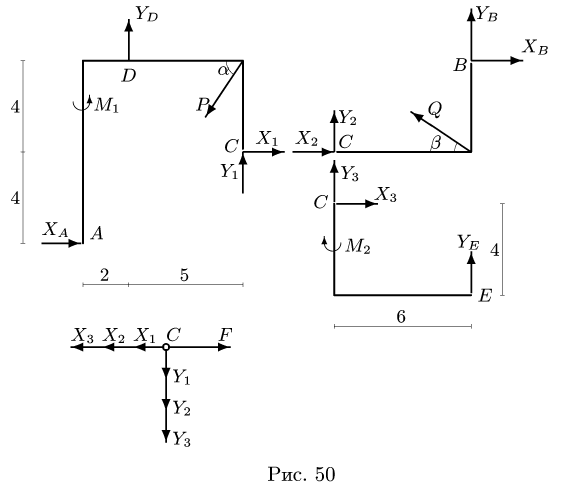
1. Расчленяем конструкцию на три отдельных тела ADC, СВ, СЕ и сочленяющий шарнир С в качестве четвертого тела. Считая, что каждое из трех тел в точке сочленения взаимодействует только с осью шарнира С, действие оси шарнира на тело заменяем ее реакциями (рис. 50).

2. Для каждого из тел (АС, ВС, ЕС) записываем по три уравнения равновесия — два уравнения проекций и уравнение моментов относительно точки С 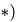. Для системы сил, сходящихся в шарнире С, составляем два уравнения равновесия в проекциях (рис. 50). Получаем следующую систему уравнений:

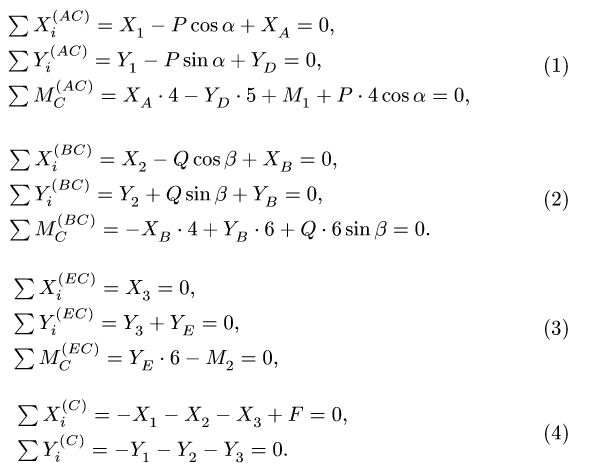
4. Решаем систему 11 уравнений с 11 неизвестными четов в кН записываем в таблицу:

5. Выполняем проверку решения, составляя дополнительное уравнение равновесия для нерасчлененной системы (рис. 51). Моментную точку К выбираем так, чтобы в уравнения вошли все проверяемые величины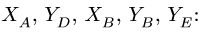

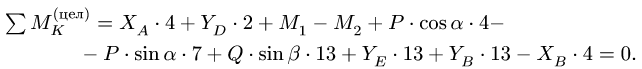
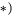В качестве моментной точки можно выбирать любую, в том числе и не принадлежащую телу.

Замечание. Предложенный способ расчета не является единственным. Например, если из трех частей, соединенных в одном шарнире, можно отделить одну, имеющую в качестве опоры подвижный шарнир (часть СЕ, рис. 50), то получится система двух тел, одно из которых (СЕ) имеет три неизвестные реакции. Определить эти реакции можно из системы трех уравнений равновесия этой части.

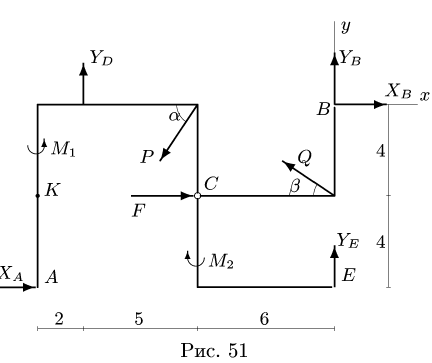
Затем следует рассмотреть оставшуюся часть, состоящую их двух еще нерасчлененных тел. В качестве дополнительной нагрузки к ним будет приложены (в противоположную сторону) две реакции отброшенной третьей части.