Расчет переходных процессов

Содержание:

Расчет переходных процессов методами наложения, спектральным и операторным:

Расчет переходного процесса при включении линейной цепи на напряжение u(t), являющееся любой функцией времени, может быть произведен методом наложения, если заменить кривую напряжения ступенчатой кривой (рис. 17.1). Тогда можно считать, что в момент времени t = 0 цепь включается на постоянное начальное напряжение u(0), а затем на ряд смещенных на равные промежутки времени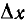

Ток или напряжение любой ветви при переходном процессе можнo найти из суммы токов, вызываемых отдельными постоянными составляющими напряжения. Для применения этого метода необходимo предварительно рассчитать переходный ток или напряжение исследуемой ветви цепи по заданному постоянному входному напряжению U₀ или току I₀ и найти зависимую от времени переходную функцию К(t), связывающую искомую и заданную величины Например, при включении цепи г, L на постоянное напряжение ток

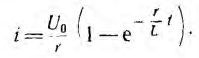
Следовательно, переходная функция

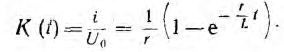
В данном случае она имеет размерность проводимости и называется переходной проводимостью

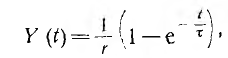
где 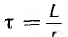постоянная времени этой цепи.

Для постоянного напряжения, включенного позже на время х, переходная проводимость

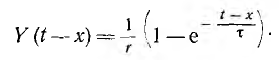
Аналогичным образом определяется любая переходная функция К (t). Например, напряжение на индуктивности при включении цепи г, L на постоянное напряжение U₀ и переходная функция соответственно равны:

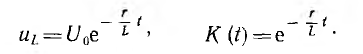
В этом случае переходная функция безразмерна. Переходная функция в принципе сразу определяет выходную величину, так как дает численное значение (но не размерность!) выходной величины, когда входная (U₀ или I₀) равна единице.

Составляющая переходного тока от напряжения u(0), включаемого в начальный момент, равна У (t) и (0), а от скачка напряжения 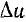, включаемого в момент х + 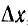, равняется Y (t — х — 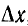). В результате приближенное значение искомого переходного тока будет:

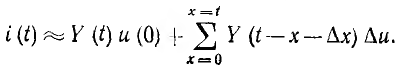
Точное значение тока i (t) получится при переходе 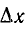в пределе к бесконечно малым промежуткам времени dx. Тогда

и ток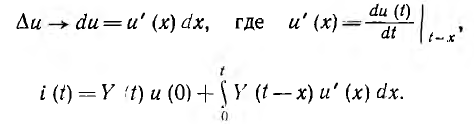

Это выражение называется интегралом Дюамеля. При определении напряжения какой-либо ветви в интеграле Дюамеля вместо переходной проводимости должна стоять соответствующая переходная функция.

Далее в виде примера определен ток при включении цепи г, L на затухающее по показательному закону напряжение 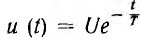, где Т — постоянная времени, характеризующая скорость затухания u(t). Переходные проводимости для этого случая даны выше, a

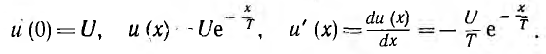
После подстановки этих величин в интеграл Дюамеля и интегрирования определяется искомый ток:

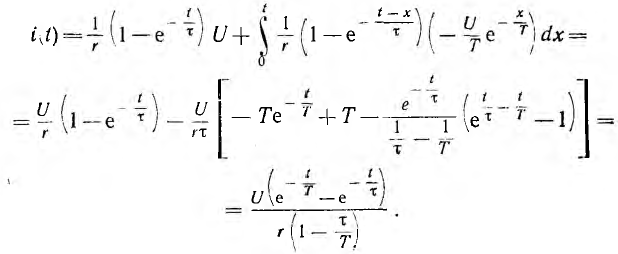
В частном случае, когда τ= Т, получается неопределенность, которая после раскрытия дает:

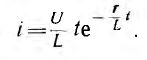
Во всех случаях переходный ток положителен и имеет максимум i_m, определяемый обычным образом. При τ = Т

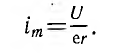
Применение метода наложения удобно также в тех случаях, когда напряжение, на которое включается цепь, представляет собой кусочно-аналитическую кривую, имеющую разрывы. При этом переходный ток определяется как сумма интегралов Дюамеля за время отдельных участков u (t), причем в их первых членах У (t) u (0) напряжение u (0) равно разности приложенных напряжений после и до разрыва, с которого начинается данный участок.

Импульсный интеграл Дюамеля

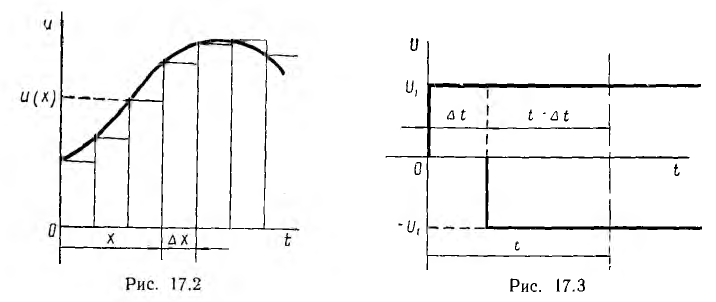
Метод наложения может быть также применен, если заданное входное напряжение u (t) представить в виде следующих друг за другом прямоугольных импульсов напряжения u (х) малой длительности 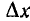(рис. 17.2) с последующим наложением выходной величины, например тока цепи, от каждого импульса напряжения с учетом его величины и сдвига во времени.

Прямоугольный импульс (рис. 17.3) характеризуется интенсивностью 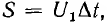равной произведению амплитуды импульса U₁ на его длительность 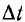. Импульс с интенсивностью S = I называется единичным.

Один прямоугольный импульс может быть представлен алгебраической суммой двух одинаковых скачков постоянного напряжения +U_l и —U₁ из которых второй возникает на время 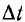позже первого. Тогда ток i₁(t) от рассматриваемого импульса напряжения в момент t определяется с помощью переходной проводимости, которая для первого скачка равна У(t) а для второго

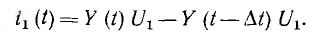
Если на цепь воздействует единичный импульс напряжения, т. е. 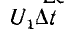= 1, предыдущее выражение получает вид:

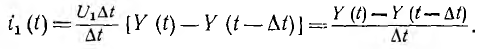
При переходе к пределу единичный импульс превращается в так называемую единичную импульсную функцию, а ток

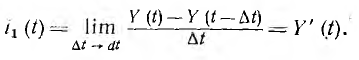
Таким образом, аналогично численному равенству переходной проводимости Y (t) току от единичного скачка напряжения, при единичной импульсной функции напряжения ток равен производной от Y (t). Поэтому Y'(t) называется импульсной переходной проводимостью.

Для установления связи между искомым током i (t), заданным напряжением произвольной формы, разбитым на элементарные импульсы u (х), и импульсной переходной проводимостью, можно идти тем же путем, как и при выводе интеграла Дюамеля, но проще это сделать, интегрируя его по частям:

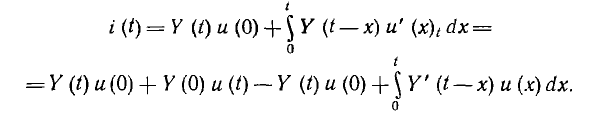
Отсюда получается импульсный интеграл Дюамеля:

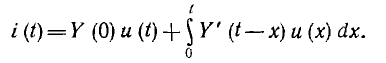
В общем случае в импульсный интеграл Дюамеля вместо u (х) следует подставить заданную входную величину, а взамен Y' (t — х) — соответствующую импульсную переходную функцию К' (t — х).

Далее в виде примера решается та же задача — определение переходного тока i (t) при включении цепи г, L на напряжение u (t) = 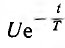. Здесь

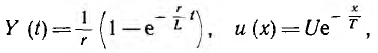
Y' (t — x) есть производная функции Y (t — x) по ее аргументу t — x, или, что то же самое, ее производная по t:

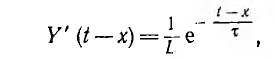
где 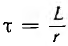— постоянная времени цепи. Из-за наличия индуктивности Y (0) = 0, ток

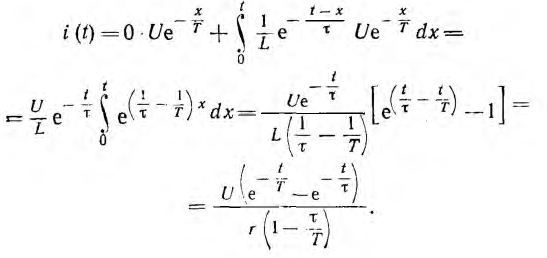
Таким образом получен тот же результат, что и при применении первой формы интеграла Дюамеля, но вычисления в данном примере несколько упростились.

Область применения метода наложения

Из изложенного видно, что метод наложения позволяет найти выходную величину переходного процесса по заданной или полученной путем аппроксимации аналитической зависимости входной величины от времени. При этом следует применять ту форму интеграла Дюамеля, для которой подынтегральное выражение упрощается. Очевидно, что метод наложения применим только в случае интегрируемых функций.

Спектральный метод

Прямое н обратное преобразование Фурье:

Для расчета переходных процессов при включении цепи на непериодическое напряжение было применено его разложение на скачкообразные или импульсные напряжения с последующим применением принципа наложения. Эту задачу также можно решить, если представить непериодическую функцию в виде суммы гармоник.

Так как каждая гармоника ряда Фурье может быть записана в комплексной форме:

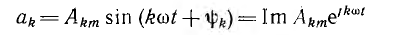
(А_кm — комплексная амплитуда), весь ряд Фурье может быть также записан в комплексной форме:

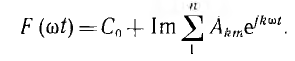
Коэффициенты этого ряда, т. е. комплексные амплитуды гармоник, могут быть определены из данных выражений для В_кm и С_кm-

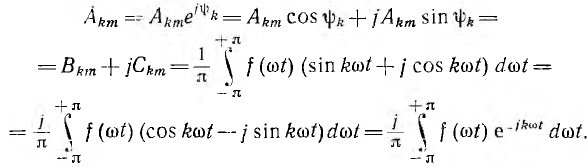
Комплексная амплитуда гармоники k периодической функции 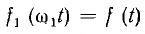с периодом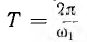

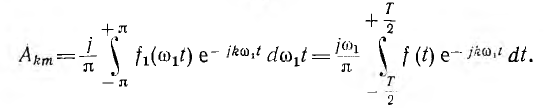
Непериодическую функцию можно рассматривать как предельный лучай периодической, у которой период Т стремится к бесконечности. Тогда разница в частоте 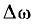между двумя соседними гармониками будет стремиться к dω. Так как частота основной (первой) гармоники 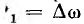, она также стремится к dω. Частота 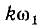гармоники k должна быть обозначена через ω. Тогда общее выражение комплексной амплитуды гармоники частоты ω получает вид:

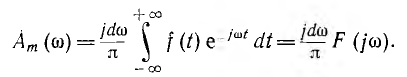
Таким образом, воздействие на цепь непериодической функции i(t) может быть заменено суммарным воздействием бесконечно большого числа бесконечно малых гармоник, т. е. спектра А_m (ω). Относительное значение амплитуд гармоник пропорционально комплексной функции частоты F (jV), имеющей вид интеграла Фурье:

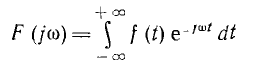
и называемой спектральной характеристикой или спектральной плотностью функции f(t). Эта характеристика может быть записана в показательной форме:

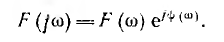
Тогда F (ω) называется амплитудно-частотной, а 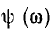— фазо-частотной характеристикой.

Преобразование f (t) в F (jω), т. е. прямое преобразование Фурье, возможно, если интеграл Фурье имеет конечное значение. Так как 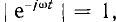, для этого достаточно, чтобы интеграл

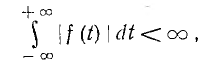
чего, например, не будет, если f (t) — постоянная величина или синусоидальная функция.

Первым этапом спектрального метода расчета переходных процессов является преобразование оригинала f(t) в его изображение F (jω). Если U (jω) является спектральной характеристикой напряжения, спектральная характеристика тока I (jω) может быть найдена из закона Ома по известному комплексному сопротивлению Z (jω) или проводимости Y (jω) цепи, в общем случае являющимися также комплексными функциями частоты. Тогда

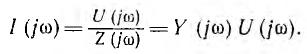
В общем случае при задании какой-либо функции с характеристикой F₁ (jω), воздействующей на вход цепи, характеристика искомой функции выхода

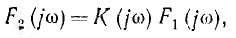
где К (jω) — так называемая передаточная функция. При изменении частоты со передаточная функция изменяется и по вели чине и по фазе. В отличие от аналогичной величины — переходно функции, которая характеризовала переходный процесс при воздействии на цепь постоянного напряжения, передаточная функция К (jω) характеризует установившийся процесс при синусоидальном воздействии.

После определения спектральной характеристики, т. е. изображения искомой величины, должен быть найден оригинал. Для вывод формулы обратного преобразования F (jω) в f (t) может быть такж использован переход от дискретного ряда к непрерывному.

Ряд Фурье в комплексной форме имеет вид:

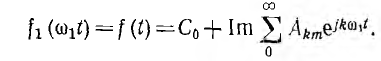
Учитывая, что мнимая часть любого комплексного числа F

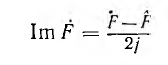
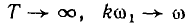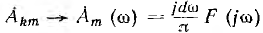(F— сопряженный комплекс), после переходов и получают следующее значение непериодической функции:

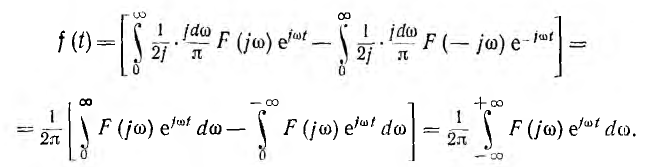
Постоянная составляющая (ω = 0) учтена тем, что нижний предел исходных интегралов взят равным нулю.

Это обратное преобразование Фурье служит для получения искомой функции времени по ее спектральной характеристике.

Необходимо отметить, что отрицательная частота имеет лишь математический смысл. Она возникла в результате замены синусоид показательными функциями .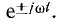

Пример применения спектрального метода

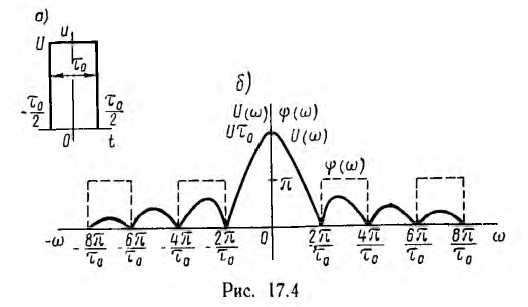
В качестве примера рассматривается переходный процесс включения цепи г, L на прямоугольный импульс напряжения U продолжительностью т₀. После окончания импульса контур остается замкнутым.

Для упрощения удобно представить импульс существующим с момента времени 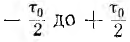(рис. 17.4, о). Так как вне этого промежутка времени f (t) = 0, интеграл Фурье вычисляется только для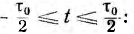

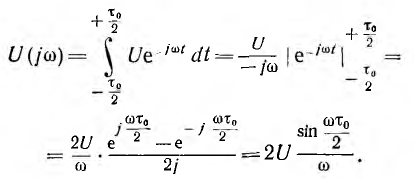
Это и есть спектральная плотность, которая в данном случае вещественна и изображается вектором, совпадающим с осью вещественных.

Счедовательно, фаза спектральной плотности равна нулю, когда дробь 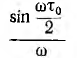- положительна, и равна π, когда эта дробь отрицательна. Амплитудно-частотная характеристика, очевидно, равна:

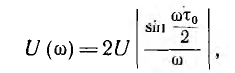
откуда U (0) = 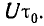. Амплитудно-частотная и фазо-частотная характеристика изображены на рис. 17.4, б.

Так как сопротивление цепи 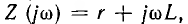, спектральная характеристика тока

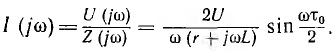
Переходный ток находят с помощью обратного преобразования Фурье:

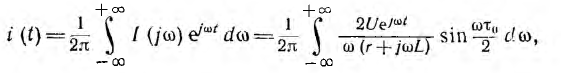
что требует вычисления интеграла сравнительно сложной функции Решение этой же задачи методом наложения (включение цепи на напряженние U при t = 0 и на - U при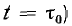значительно проще.

Если требуется найти напряжение u_L (t) на индуктивности, то, та как

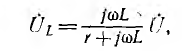
передаточная К (jω) и спектральная U_L(jω) функции получают вид,

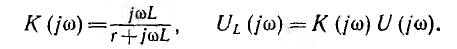
Определение искомого напряжения

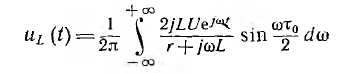
также связано с вычислением интеграла.

Область применения спектрального метода

Как видно из изложенного, непосредственное применение спектрального метода имеет следующие ограничения:

1. он может применяться только для абсолютно интегрируемых функций;
2. этот метод принципиально не учитывает начальных условий, поэтому он применим только для задач с нулевыми начальными условиями.

Некоторые искусственные приемы позволяют обойти эти ограничения, но при этом расчеты еще больше усложняются. Как было видно из рассмотренного примера, наиболее трудным этапом является обратное преобразование, связанное с интегрированием сложных функций. В ряде случаев интегралы не берутся и приходится прибегать к приближенным расчетам. Очевидно также, что спектральный метод как разновидность метода наложения применим только для линейных цепей.

Ценность спектрального метода заключается в том, что расчет переходных процессов сводится к расчету установившихся режимов в цепях синусоидального тока и, следовательно, к возможности получения ответа без составления и решения дифференциальных уравнений. Задачи могут быть решены при помощи определенных из опыта или заданных аналитически или графически амплитудно-частотных харак теристик входных напряжений и токов цепи и передаточных функций Этот метод в чистом или приближенном виде широко применяется в тео рии автоматического регулирования и радиотехнике.

Операторный метод

Прямое и обратное преобразования Лапласа:

Пусть функция f (t), равная нулю при t < О, не удовлетворяет условию абсолютной интегрируемости. Тогда преобразование Фурье к ней неприменимо. Если образовать вспомогательную функцию

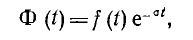
где σ — положительное вещественное число, и взять σ достаточно большим, Ф (t) для большинства функций f (t) будет настолько быстро убывать на бесконечности, что

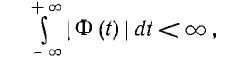
т. е. условие абсолютной интегрируемости будет выполнено. Тогда к Ф (t) могут быть применены преобразования Фурье.

Прямое преобразование после подстановки значения Ф (t) и замены нижнего предела — 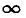на нуль, так как при t < О функция f (t) = О, получает вид:

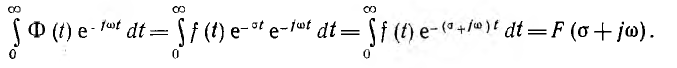
Если обозначить через p комплексное число 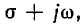называемое оператором, предыдущее выражение будет:

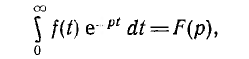
здесь в левой части стоит интеграл Лапласа. Полученное соотношение называется прямым преобразованием Лапласа. С его помощью находят операторное изображение F (р) оригинала f(t).

Обратное преобразование Фурье для функции F (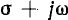) может быть получено из формулы для обратного преобразования F (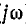), если заменить F (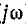) на F (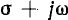) и, соответственно, пределы ± 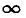на ;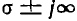

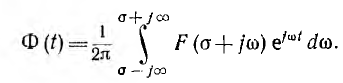
После умножения левой и правой частей на 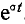, замены 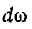на равное ему 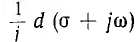и подстановки 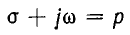получается обратное преобразование Лапласа

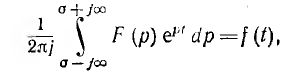
позволяющее найти оригинал по изображению. Связь между оригиналом и изображением условно записывается так:

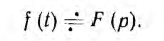
Как видно из вывода, преобразования Фурье являются частным случаем преобразований Лапласа для случая, когда комплекс р = σ -+ jω становится мнимым числом jω. Поэтому применимость интеграл Лапласа шире, чем интеграла Фурье, так как не накладывается требе вание абсолютной интегрируемости функции f(t). Последняя должнa лишь удовлетворять условиям Дирихле.

Прямое преобразование Лапласа весьма широко применяете! для расчета переходных процессов, так как операции с изображениями, как будет видно далее, достаточно просты. Для обратного перехода от изображений к оригиналам в большинстве случаев не используется сложное обратное преобразование Лапласа, а применяется более простой прием, обоснованный далее.

Рассматриваемый метод получил название операторного. Первой работой, в которой применялись преобразования Лапласа для решения дифференциальных уравнений, была монография Ващенко-Захарченко, опубликованная в 1862 г. В конце XIX века Хевисайд впервые успешно применил операторный метод к расчету электромагнитных переходных процессов, но не дал его обоснования. Дальнейшему развитию и обоснованию операторного метода были посвящены многочисленные работы зарубежных и советских ученых — Карсона, Вагнера, Эфроса и Данилевского, Лурье и др.

Операторные изображения простейших функций

Из основных свойств определенных интегралов вытекают следующие два следствия для изображений. Если известны изображения нескольких функций

то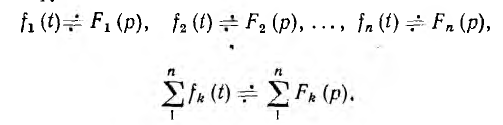

т. е. изображение суммы функций равно сумме их изображений. При А = const

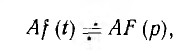
т. е. при умножении функции на постоянную величину изображение функции должно быть умножено на эту величину. Изображение постоянной величины

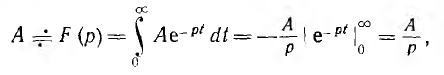
т. е. изображением постоянной является она сама, деленная на р.

Изображение показательной функции

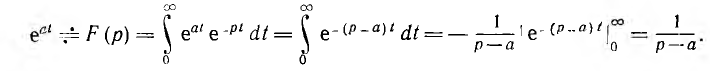
Из этого соотношения могут быть найдены изображения следующих функций:

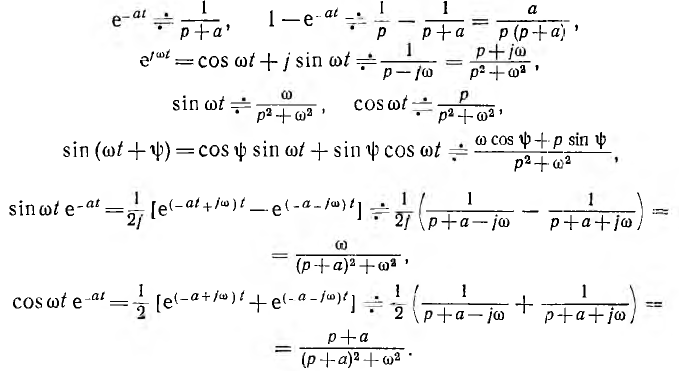
В справочниках приведены изображения многих других функций.

Изображения производной и интеграла функции

Если известны начальное значение f(0) функции f (t) и ее изображение 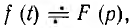то изображение производной f '(t) можно получить, интегрируя по частям:

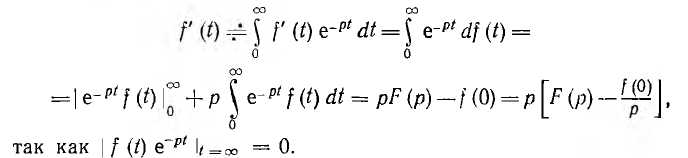
Изображение второй производной

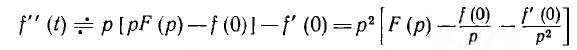
и аналогично изображение производной n-го порядка:

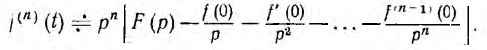
Особый интерес для практики представляет случай, когда начальные значения функции и ее производных равны нулю. Тогда

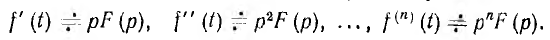
Изображение ψ (р) определенного интеграла

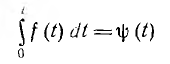
можно найти по известному изображению подынтегральной функции f (t) 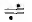F(р) из следующего сопоставления:

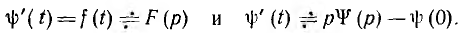
Следовательно, так как начальное значение интеграла ,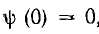

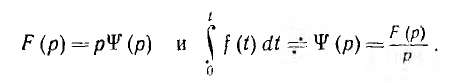
Изображение неопределенного интеграла можно найти, выражая его через определенный с переменным верхним пределом t:

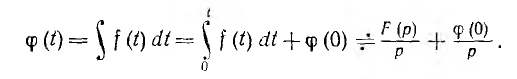
Таким образом, ненулевые начальные условия учитываются в выражениях для изображений. При нулевых начальных условиях дифференцирование и интегрирование оригиналов заменяются умножением и делением изображений на оператор р, подобно тому как умножение и деление чисел заменяется более простыми действиями — сложением н вычитанием логарифмов чисел.

Законы электрических цепей в операторной форме

Пусть цепь с последовательным соединением г, L, С при ненулевых начальных условиях включается на напряжением u(t). Тогда

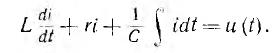
Переход от i (t) и u (t) к их изображениям I (р) и U (р) превращает интегро-дифференциальное уравнение в алгебраическое:

Отсюда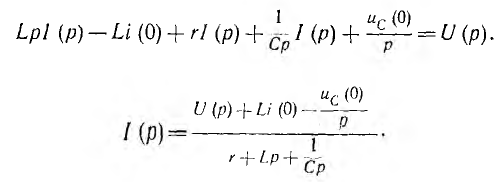

Это выражение представляет собой аналог закона Ома в операторной форме для переходного процесса при ненулевых начальных условиях. В знаменателе стоит операторное сопротивление:

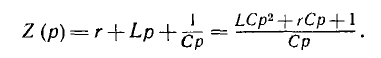
Оно может быть получено из комплексного полного сопротивления для синусоидального тока 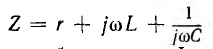заменой jω на р, что соответствует переходу от преобразования Фурье к преобразованию Лапласа.

В частном случае нулевых начальных условий, т. е. при i (0) = 0 и u_с (0) = 0,

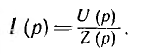
В общем случае сложной цепи ее операторное сопротивление имеет аналогичный вид:

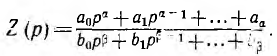
Как показано далее, степени аир могут отличаться не больше, чем на единицу.

Операторное сопротивление Z (р) и операторная проводимость 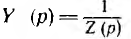также могут рассматриваться как операторные передаточные функции. При нулевых начальных условиях передаточной является операторная функция К (р), на которую надо умножить функцию F₁ (р) — напряжение или ток на входе, чтобы получить функцию F₂ (р), характеризующую выходную величину:

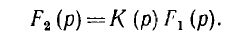
Вид функции К (р) совпадает с рассмотренной функцией К (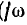). Последняя является комплексной частотной характеристикой передаточной функции.

Законы Кирхгофа в их первой форме 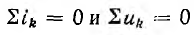могут быть записаны в операторном виде:

Второй закон Кирхгофа в операторном виде для второй формы его записи при нулевых начальных условиях и отсутствии взаимной индукции имеет вид:

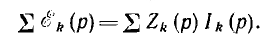
В общем случае этот закон записывается следующим образом:

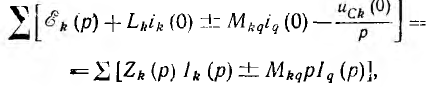
где 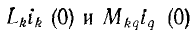— изображения начальных напряжений, уравновешивающих э. д. с. само- и взаимоиндукции;

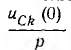--изображение начального напряжения на емкости;

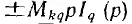— изображения напряжений взаимной индукции.

При расчете переходных процессов в сложных цепях операторным методом составляется алгебраическая система уравнений для изображений по законам Кирхгофа или по методам, из них вытекающим: наложения, контурных токов, эквивалентного источника и т. д. При этом необходимо учесть ненулевые начальные условия. Решение системы уравнений дает изображения искомых токов и напряжений. Эти изображения, как видно из приведенного примера, имеют вид рациональных дробей.

Для перехода от изображений к оригиналам можно использовать таблицы, подобные приведенным в п. 2 этого параграфа. При отсутствии этих данных может быть применено обратное преобразование Лапласа, а для большинства функций, встречающихся в электротехнической практике,— более простое преобразование, основанное на теореме разложения.

Теорема разложения

В большинстве случаев изображение представляет собой такую рациональную дробь:

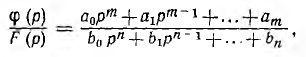
у которой 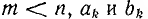— вещественные числа, а корни 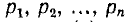уравнения F (р) = 0 не кратны и не равны корням уравнения ϕ (р) = 0. Тогда дробь может быть разложена на простые дроби:

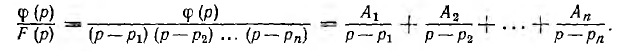
Для определения коэффициента А_к следует обе части равенства умножить на р — p_k:

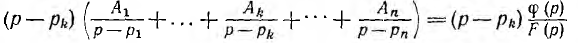
и устремить р к р_к. Тогда левая часть превратится в А_к, а правая — в неопределенность 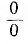раскрытие которой дает:

Следовательно,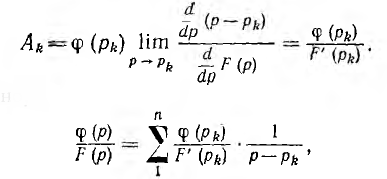

так как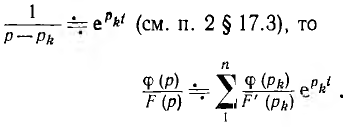

Это и есть теорема разложения, позволяющая по изображению в виде рациональной дроби найти оригинал, равный сумме оказательных функций времени, умноженных на постоянные коэффициенты. Если при этом один из корней F (р) равен нулю, соответ-.твующая показательная функция превращается в постоянную величину.

Примеры применения операторного метода

Далее приведен ряд примеров расчета переходных процессов с переходом от изображения к оригиналу по таблицам и теореме разложения. Некоторые из этих задач решены другими методами, что позволит оценить эффективность операторного метода.

1. При включении цепи г, L на затухающее по показательному закону напряжение u(t)=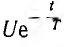 его изображение и операторное сопротивление цепи будут:

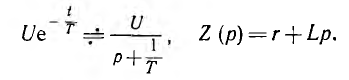
Изображение тока U

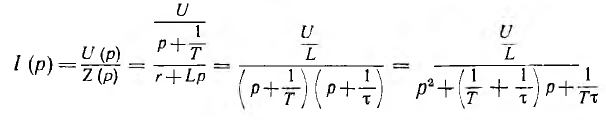
представляет собой рациональную дробь. Корни знаменателя и его производная, соответственно, равны:

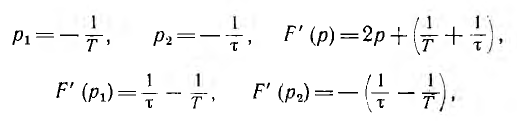
и по теореме разложения оригинал

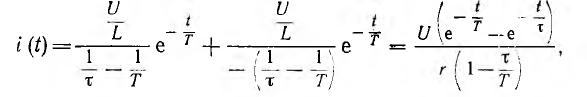
что совпадает с решением методом наложения.

2. При включении цепи г, L, С на постоянное напряжение U₀ npи нулевых начальных условиях

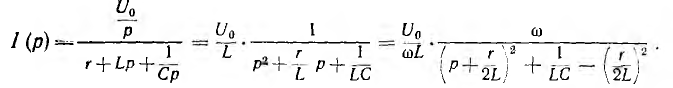
Правая часть этого выражения совпадает с изображением 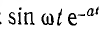приведенным в п. 2 этого параграфа, если принять

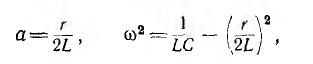
причем ω — вещественное число. Следовательно, ток

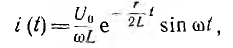
что совпадает с результатом, полученным  классическим методом для случая 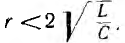. Для случая 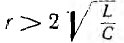полученное выражение можно преобразовать, подставив значение ω, которое в этом случае будет мнимым числом.

Для перехода к оригиналу можно также применить теорему разложения. Здесь

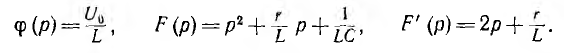
Уравнение F (р) = 0 имеет корни

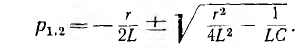
Тогда

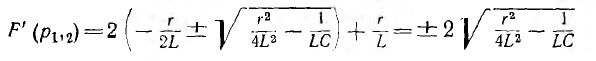
и оригинал по теореме разложения будет:

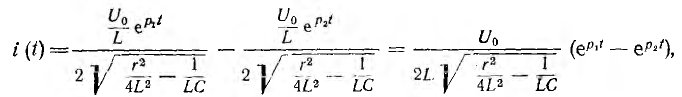
что также совпадает с решением, полученным ранее классическим методом.

3. Примером расчета переходных процессов при ненулевых начальных условиях может служить задача на короткое замыкание цепи г, L, С, ранее включенной на синусоидальное напряжение u(t) = .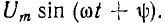

В момент замыкания при t = 0 приложенное напряжение u(t) оказывается отключенным от цепи, т. е. u (0) = 0 и U(р) = 0, а ток цепи напряжение на емкости, соответственно, равны:

.

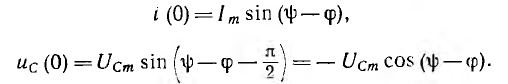Tогда изображение тока

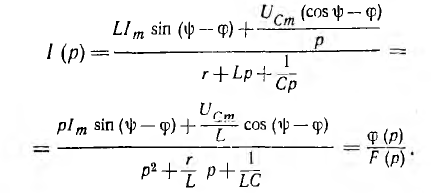
Знаменатель F (р) этой рациональной дроби и его корни р₁ и р₂ те же, что и в предыдущей задаче. Тогда по теореме разложения переходный ток цепи

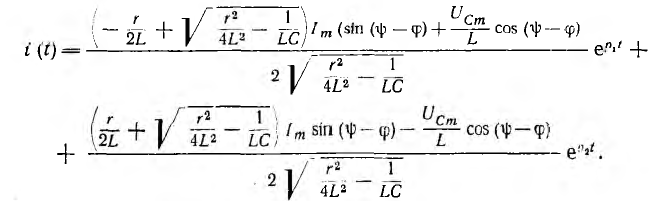
В зависимости от знака подкоренной величины ток будет иметь апериодический или колебательный характер.

4. Примером расчета переходных процессов в цепях со взаимной индукцией может служить задача включения трансформатора на постоянное напряжение, решенная в  классическим методом.

Замена в системе уравнений трансформатора для синусоидального тока 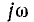 на р, а комплекса приложенного напряжения U на изображение 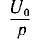постоянного напряжения U₀ сразу дает систему уравнений для изображений:

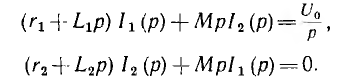
Решение этой системы:

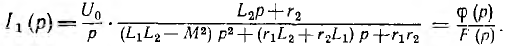
Уравнение F (р) = 0, помимо отрицательных вещественных корней p₁ и р₂, совпадающих с корнями характеристического уравнения при Решении классическим методом, имеет корень р₀ = 0, который при подстановке в формулу теоремы разложения даст принужденный ток I₀ = 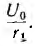Две другие составляющие тока (t) являются экспонентам с показателями р₁t и р₂t.

Знаменатель изображения тока

1 (D)-_IzM&__

2 w - (ЦЦ - т р* + (ПЦ + г2Ц) р + г1гг

не имеет корня, равного нулю, следовательно, ток i₂ {t) содержит только две экспоненты с теми же показателями.

5. Рассматривая включение цепи г, L на переменное напряжение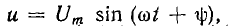, следует его заменить комплексом

U_m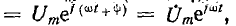 последний — операторным изображением.

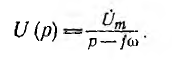
Так как операторное сопротивление 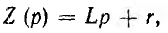изображение тока

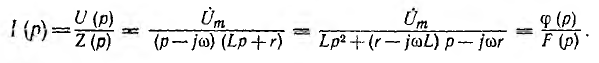
Корни и производная знаменателя F (р) имеют вид:

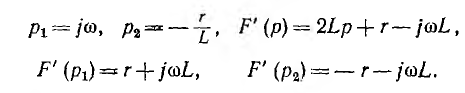
В соответствии с этим теорема разложения дает

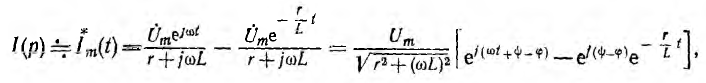
после чего можно перейти к мгновенному значению тока

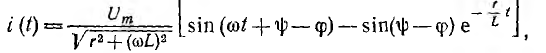
совпадающему с решением классическим методом.

Применение операторного метода

Из теории и примеров видно, что операторный метод, как и классический, может применяться для расчета переходных процессов только в линейных цепях. Операторный метод имеет следующие достоинства:

1. он обобщает методику составления уравнений и расчета цепе?! при переходных процессах 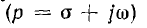и установившихся режимах постоянного (р = 0) и синусоидального переменного (р = 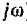) токов;
2. благодаря алгебраизации дифференциальных уравнений или применению операторных изображений и известных из теории установившихся режимов методов расчета цепей, получение уравнения для юбражения искомой функции весьма упрощается;
3. отпадает необходимость определения из начальных условий постоянных интегрирования, свойственная классическому методу; начальные условия учитываются в операторных изображениях.

Вместе с тем как операторный, так и классический методы требуют решения того же самого характеристического уравнения, что затруднительно при высокой степени последнего.