
Прямые и плоскости в пространстве с примерами решения
Содержание:
Прямые и плоскости в пространстве
Основные геометрические фигуры в пространстве: точка, прямая и плоскость. Плоскость мы представляем в виде поверхности стола (рис. 1 а). Плоскость как и прямая бесконечна. На рисунке представляем только часть плоскости (рис. 1 б). Однако, мы предполагаем, что се можно продолжить в любую сторону и на чертеже изображаем в виде параллелограмма (рис. 1 б). Плоскости обозначаем прописными греческими буквами 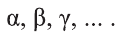
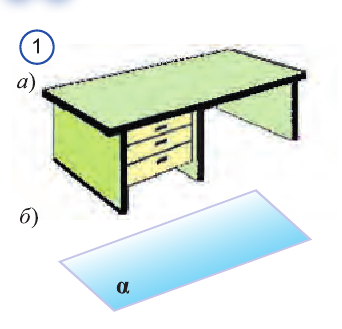
Две прямые в пространстве могут пересекаться или не пересекаться (рис. 2). В пространстве две прямые, не лежащие в одной плоскости, называются скрещивающимися (рис. 2 а).
Прямые, лежащие в одной плоскости и имеющие только одну общую точку, называются пересекающимися прямыми (рис. 2 б).
Прямые, лежащие в одной плоскости и непересекающиеся, называются параллельными прямыми (рис. 2 в). 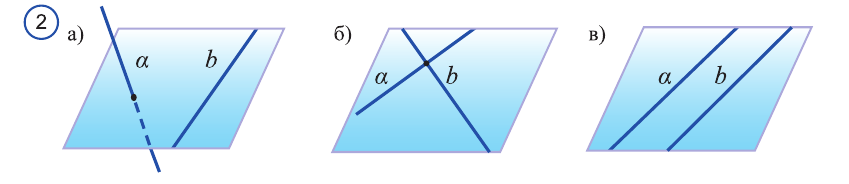
Примером скрещивающихся прямых могут быть две дороги, одна из которых проходит по эстакаде, а другая под эстакадой (рис. 3). Точно также, прямые, на которых лежат ребра MN и 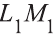 параллелепипеда являются скрещивающимися (рис. 4).
параллелепипеда являются скрещивающимися (рис. 4).

Как расположены относительно друг друга прямая и плоскость в пространстве?
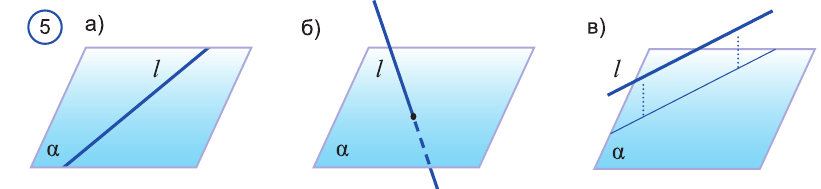
Прямая может лежать на плоскости (рис. 5.а), пересекать ее (рис. 5.6) или не пересекать, то есть иметь или не иметь с плоскостью общую точку (рис. 5.в). В последнем случае говорят, что прямая параллельна плоскости.
 Карандаш, лежащий на столе, дает представление о прямой, лежащей на плоскости (рис. 6 а), стрела, направленная в цель (рис. 6 б) - о прямой пересекающей плоскость, гимнастическое бревно и пол спортивного зала - о прямой параллельной плоскости (рис. 6 в).
Карандаш, лежащий на столе, дает представление о прямой, лежащей на плоскости (рис. 6 а), стрела, направленная в цель (рис. 6 б) - о прямой пересекающей плоскость, гимнастическое бревно и пол спортивного зала - о прямой параллельной плоскости (рис. 6 в). 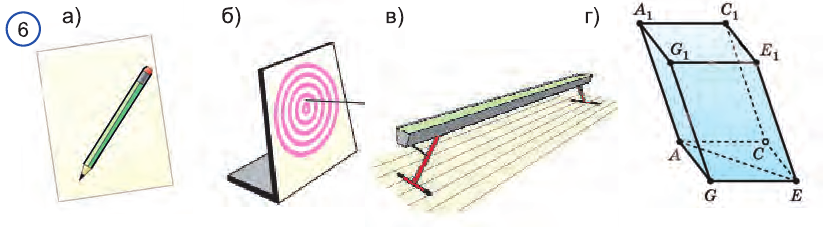
Точно также, прямая, содержащая диагональ АЕ параллелепипеда AGEC (рис. 6.г), лежит в плоскости основания, пересекает плоскость грани 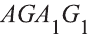 и параллельна плоскости верхнего основания
и параллельна плоскости верхнего основания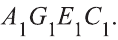
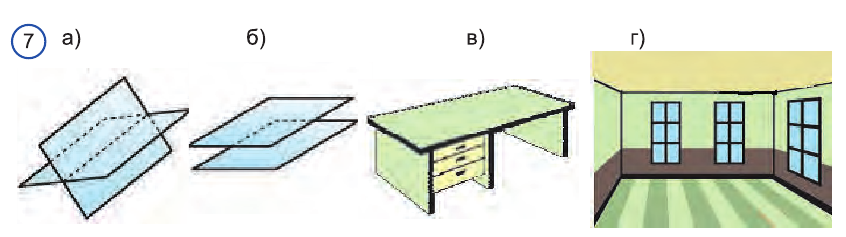
Теперь рассмотрим взаимное расположение плоскостей в пространстве. В пространстве плоскости могут пересекаться по прямой (рис. 7 а) или не иметь общих точек (рис. 7 б). Тогда говорят, что эти плоскости соответственно пересекаются или параллельны.
Крышка стола и его боковушка, изображенные на рисунке 7в дают представление о пересекающихся плоскостях, а пол и потолок в помещении (рис. 7 г) - о параллельных плоскостях.
Аналогично, не противоположные боковые грани параллелепипеда (рис. 4), дают представление о пересекающихся плоскостях, а его верхняя и нижняя грани и противоположные боковые грани - о параллельных плоскостях.
Знаки параллельности - " ||" используют не только для параллельных прямых, но и для параллельных прямой и плоскости и для параллельных плоскостей:
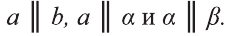
В стереометрии, как и в планиметрии некоторые геометрические свойства фигур принимают без доказательств. Следующие свойства плоскостей называем группой аксиом С и принимаем их без доказательств.
 Если три точки не лежат на одной прямой, то через них можно про-вести плоскость, и притом только одну.
Если три точки не лежат на одной прямой, то через них можно про-вести плоскость, и притом только одну.
 Если две точки прямой принадлежат одной плоскости, то все точки этой прямой принадлежат этой плоскости.
Если две точки прямой принадлежат одной плоскости, то все точки этой прямой принадлежат этой плоскости.
 Если две плоскости имеют общую точку, то они имеют общую прямую, проходящую через эту точку.
Если две плоскости имеют общую точку, то они имеют общую прямую, проходящую через эту точку.
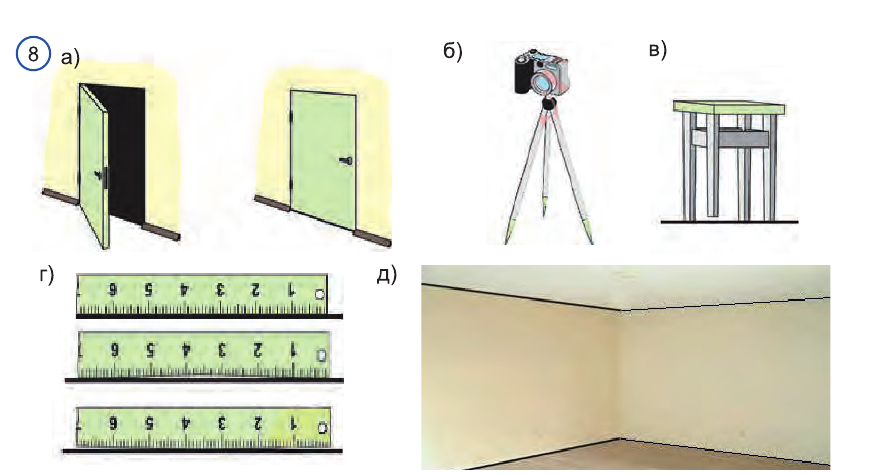
Активизирующее упражнение. На какие аксиомы можно сослаться при объяснении следующих случаев на рисунке 8?
Эти три аксиомы вместе с введенными в планиметрии аксиомами являются основой стереометрии. Необходимо напомнить, что все фигуры, рассматриваемые в планиметрии, считались расположенными в одной плоскости. В стереометрии таких плоскостей бесконечно много и пред-полагается, что на каждой из них имеют место все аксиомы планиметрии и все доказанные в ней свойства. Поэтому, аксиомы планиметрии в курсе стереометрии рассматриваются с точки зрения стереометрии.
Теорема 2.1 Через прямую и не лежащую па ней точку можно провести одну и только одну плоскость.
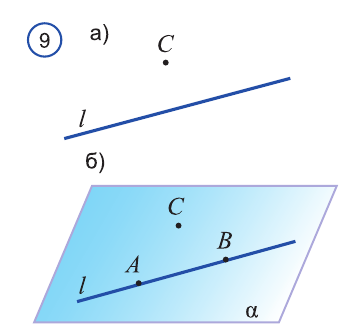
Доказательство. Пусть l - заданная прямая, а С точка, не лежащая на ней (рис. 9 а). Сначала докажем существование плоскости, о которой говорится в заключении.
Отметим на прямой l точки А и В. По условию точки А, В и С не лежат на одной прямой. Тогда по аксиоме через точки А, В и С можно провести плоскость а (рис. 9 б). А по аксиоме С2 плоскость а проходит через прямую l. Следовательно, а - искомая плоскость..
Теперь докажем, что эта плоскость единственна.
Предположим обратное: Пусть через данную прямую l и не лежащую на ней точку С можно провести еще одну плоскость 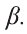 . Тогда плоскость
. Тогда плоскость 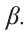 также проходит через точки А, В и С. Однако, по аксиоме
также проходит через точки А, В и С. Однако, по аксиоме 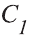 через три точки проходит только одна плоскость. Противоречие.
через три точки проходит только одна плоскость. Противоречие.
Следовательно, наше предположение неверно. Через прямую и не лежащую на ней точку можно провести одну и только одну плоскость. 
Теорема 2.2 Через две пересекающиеся прямые можно провести единственную плоскость.
Доказательство. Пусть прямые а и b пересекаются в точке С (рис. 10 а).
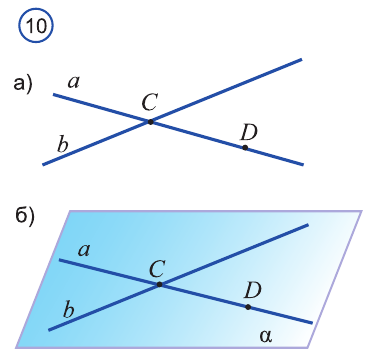
Отмстим на прямой а точку D, отличную от точки С. Тогда по доказанной теореме 1 через прямую b и не лежащую на ней точку D проходит единственная плоскость (рис. 10 б). Эта плоскость проходит через прямую а и точки С и D, лежащие на ней. Тогда, по аксиоме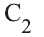 плоскость а проходит и через прямую а. Следовательно, плоскость
плоскость а проходит и через прямую а. Следовательно, плоскость 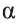 проходит через две пересекающиеся прямые.
проходит через две пересекающиеся прямые.
Докажите единственность этой плоскости самостоятельно.
Прямые и плоскости
А) Прямые и плоскости в пространстве могут располагаться по-разному.
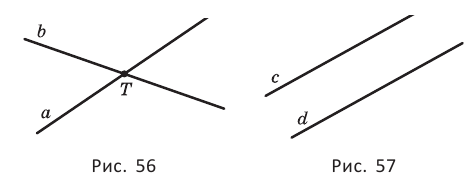
Две прямые плоскости могут иметь только одну общую точку. Такие прямые называются пересекающимися. На рисунке 56 показаны пересекающиеся прямые 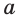 и
и 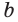 и их единственная общая точка
и их единственная общая точка 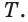 Две прямые плоскости могут не иметь общих точек. Тогда их называют параллельными. На рисунке 57 показаны параллельные прямые
Две прямые плоскости могут не иметь общих точек. Тогда их называют параллельными. На рисунке 57 показаны параллельные прямые 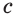 и
и 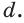 В пространстве две прямые могут быть расположены так, что они не лежат в одной плоскости, т. е. нет такой плоскости, которой бы они обе принадлежали. Такие прямые называются скрещивающимися. Представление о таких прямых дают две дороги, одна из которых проходит по эстакаде, а другая — под эстакадой (рис. 58). Такими являются прямые, которые проходят через рёбра
В пространстве две прямые могут быть расположены так, что они не лежат в одной плоскости, т. е. нет такой плоскости, которой бы они обе принадлежали. Такие прямые называются скрещивающимися. Представление о таких прямых дают две дороги, одна из которых проходит по эстакаде, а другая — под эстакадой (рис. 58). Такими являются прямые, которые проходят через рёбра 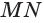 и
и 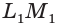 параллелепипеда
параллелепипеда 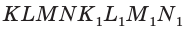 (рис. 59).
(рис. 59).

Каким может быть взаимное расположение прямой и плоскости?
Прямая может лежать в плоскости (рис. 60). Если прямая не лежит в плоскости, то она может пересекать её в некоторой точке (рис. 61) или не иметь с плоскостью ни одной общей точки (рис. 62). В последнем случае прямая и плоскость называются параллельными.
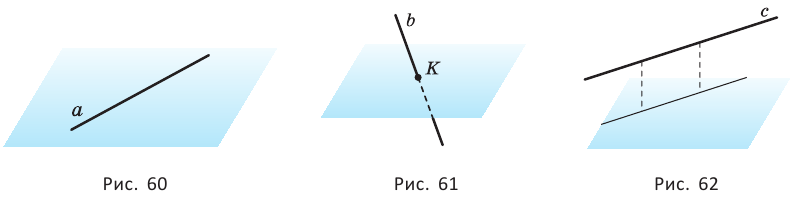
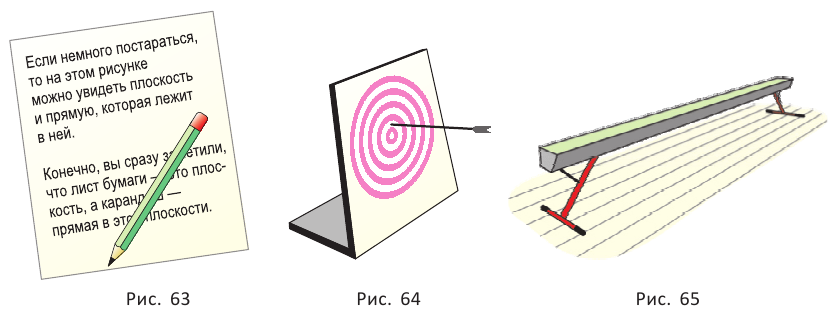
Представление о прямой, лежащей в плоскости, даёт карандаш, который лежит на столе (рис. 63), о пересекающихся прямой и плоскости — стрела, выпущенная из лука и попавшая в плоскую мишень (рис. 64), о прямой, не пересекающей плоскость, — пол в спортивном зале и гимнастическое бревно (рис. 65).
Указанные виды взаимного расположения прямой и плоскости можно проследить и на изображении параллелепипеда (рис. 66). Прямая, которой принадлежит диагональ 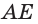 грани
грани 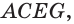 лежит в плоскости этой грани. Прямая, проходящая через ребро
лежит в плоскости этой грани. Прямая, проходящая через ребро 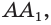 пересекает плоскость грани
пересекает плоскость грани 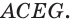 . Прямая, содержащая ребро
. Прямая, содержащая ребро 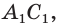 параллельна плоскости грани
параллельна плоскости грани 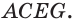
Как могут располагаться в пространстве две плоскости
Плоскости могут пересекаться по прямой (рис. 67) или не иметь общих точек (рис. 68). В соответствии с этим их называют пересекающимися или параллельными.
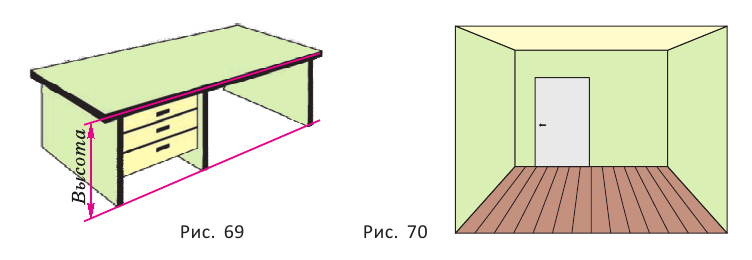
Представление о пересекающихся плоскостях дают столешница и боковина стола (рис. 69), о параллельных плоскостях — пол и потолок в помещении (рис. 70). На изображении параллелепипеда на рисунке 66 пересекающимися являются плоскости граней 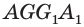 и
и 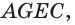 параллельными — плоскости граней
параллельными — плоскости граней 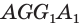 и
и 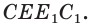
Знак 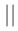 используют не только для обозначения параллельности прямых, но и параллельности прямой и плоскости и двух плоскостей. Если учесть, что прямые обозначаются строчными латинскими буквами
используют не только для обозначения параллельности прямых, но и параллельности прямой и плоскости и двух плоскостей. Если учесть, что прямые обозначаются строчными латинскими буквами 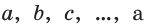 а плоскости — строчными греческими буквами
а плоскости — строчными греческими буквами 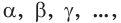 то записи
то записи 
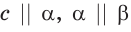 означают, что параллельными являются прямые
означают, что параллельными являются прямые 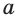 и
и 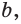 прямая
прямая 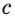 и плоскость
и плоскость 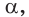 плоскости
плоскости 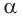 и
и 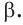
Б) Теория взаимного расположения прямых и плоскостей в пространстве основывается на следующих аксиомах.
- Аксиома 1. Если три точки не лежат на одной прямой, то через них проходит единственная плоскость.
- Аксиома 2. Если две точки прямой лежат в плоскости, то каждая точка этой прямой принадлежит плоскости. В этом случае говорят, что прямая лежит в плоскости.
- Аксиома 3. Если две плоскости имеют общую точку, то они имеют и общую прямую, проходящую через эту точку.
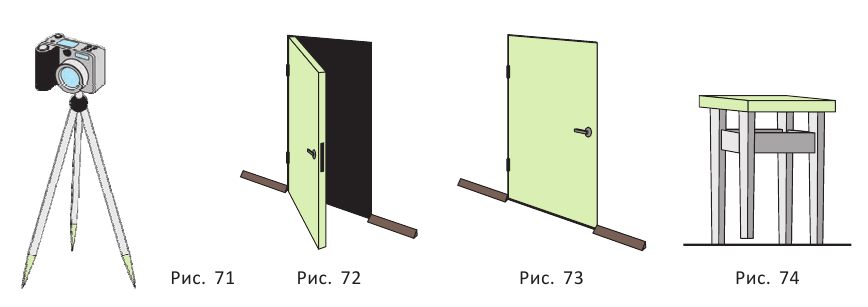
Свойство плоскости, которую фиксирует аксиома 1, часто используется на практике. Острия ножек штатива фотоаппарата (рис. 71) принадлежат одной плоскости, и поэтому положение фотоаппарата устойчивое. Дверь, закреплённая на двух петлях, не занимает определённого положения (рис. 72), но если добавить третью точку крепления — замок, то положение двери фиксируется (рис. 73). Когда ножки табурета неправильно подрезаны, то табурет стоит на трёх ножках, а четвёртая ножка висит над полом (рис. 74).
 Свойство плоскости, которое выражает аксиома 2, используют для проверки прямолинейности чертёжной линейки. Линейку прикладывают краем к поверхности стола: если край прямолинейный, то он всеми своими точками прилегает к поверхности стола (рис. 75), а если неровный, то между краем линейки и поверхностью стола есть щель (рис. 76 и 77).
Свойство плоскости, которое выражает аксиома 2, используют для проверки прямолинейности чертёжной линейки. Линейку прикладывают краем к поверхности стола: если край прямолинейный, то он всеми своими точками прилегает к поверхности стола (рис. 75), а если неровный, то между краем линейки и поверхностью стола есть щель (рис. 76 и 77).

Свойство плоскости, зафиксированное аксиомой 3, проявляется при пересечении двух смежных стен комнаты (рис. 78).
Отметим, что в стереометрии выполняются все аксиомы планиметрии и все доказанные в ней утверждения. В частности, признаки равенства и признаки подобия треугольников остаются в силе и для треугольников, лежащих в разных плоскостях.
В соответствии с аксиомой 1 плоскость определяется тремя своими точками 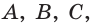 поэтому иногда плоскость обозначают тремя прописными латинскими буквами: плоскость, проходящую через точки
поэтому иногда плоскость обозначают тремя прописными латинскими буквами: плоскость, проходящую через точки 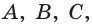 обозначают
обозначают 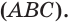
Пример №1
На рёбрах 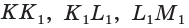 призмы
призмы 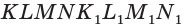 выбраны точки
выбраны точки 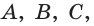 причём прямая, определённая точками
причём прямая, определённая точками 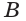 и
и 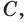 не параллельна ребру
не параллельна ребру 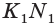 (рис. 79). Плоскости
(рис. 79). Плоскости 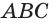 и
и 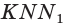 имеют общую точку
имеют общую точку 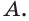 В соответствии с аксиомой 3 они имеют общую прямую. Построим её.
В соответствии с аксиомой 3 они имеют общую прямую. Построим её.
Точка 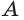 принадлежит грани
принадлежит грани 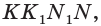 а точки
а точки 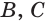 — грани
— грани 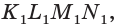 и эти грани пересекаются по прямой
и эти грани пересекаются по прямой 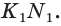 Эта прямая и прямая
Эта прямая и прямая 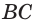 лежат в одной плоскости и не параллельны. Поэтому они пересекаются в некоторой точке. Найдём её, продлив отрезки
лежат в одной плоскости и не параллельны. Поэтому они пересекаются в некоторой точке. Найдём её, продлив отрезки 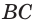 и
и 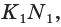 и получим точку
и получим точку 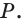
Точка 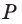 принадлежит прямым
принадлежит прямым 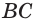 и
и 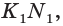 значит, она принадлежит как плоскости
значит, она принадлежит как плоскости 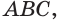 так и плоскости
так и плоскости 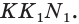 Этим же плоскостям принадлежит и точка
Этим же плоскостям принадлежит и точка 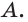 Значит, прямая, определённая точками
Значит, прямая, определённая точками 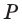 и
и 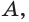 принадлежит и плоскости
принадлежит и плоскости 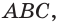 и плоскости
и плоскости 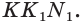 Иными словами, плоскости
Иными словами, плоскости 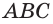 и
и 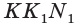 пересекаются по прямой
пересекаются по прямой 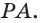
Теорема 3. Через прямую и точку вне её проходит единственная плоскость.
Доказательство: Пусть есть прямая 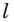 и точка
и точка 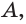 которая не принадлежит прямой
которая не принадлежит прямой 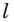 (рис. 80).
(рис. 80).
Выберем на прямой 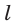 две точки
две точки 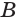 и
и 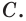 Точки
Точки 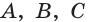 не лежат на одной прямой, поэтому по аксиоме 1 через них проходит некоторая плоскость
не лежат на одной прямой, поэтому по аксиоме 1 через них проходит некоторая плоскость 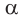 (рис. 81). Плоскость
(рис. 81). Плоскость 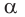 в соответствии с аксиомой 2 проходит и через прямую
в соответствии с аксиомой 2 проходит и через прямую 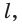 так как две её точки
так как две её точки 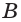 и
и 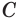 принадлежат плоскости
принадлежат плоскости 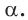

Допустим, что через прямую 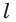 и точку
и точку 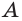 проходит ещё одна плоскость
проходит ещё одна плоскость 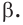 Тогда плоскость
Тогда плоскость 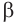 проходит как через точку
проходит как через точку 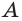 , так и через точки
, так и через точки 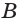 и
и 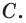 Поскольку по аксиоме 1 через три различные точки проходит единственная плоскость, то плоскость
Поскольку по аксиоме 1 через три различные точки проходит единственная плоскость, то плоскость 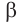 совпадает с плоскостью
совпадает с плоскостью 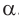 . Значит, через прямую
. Значит, через прямую 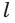 и точку
и точку 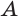 вне её проходит единственная плоскость.
вне её проходит единственная плоскость.
Теорема 4. Через две пересекающиеся прямые проходит единственная плоскость.
Доказательство: Пусть имеются две пересекающиеся прямые 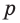 и
и 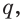 и
и 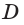 — их общая точка (рис. 82).
— их общая точка (рис. 82).
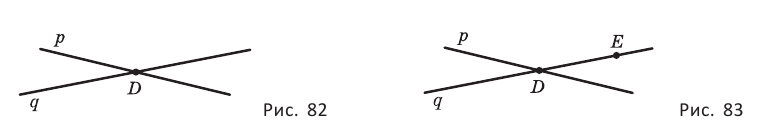
Выберем на прямой 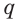 какую-либо точку
какую-либо точку 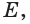 отличную от точки
отличную от точки 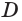 (рис. 83). В соответствии с теоремой 3 через прямую
(рис. 83). В соответствии с теоремой 3 через прямую 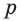 и точку
и точку 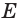 проходит единственная плоскость
проходит единственная плоскость 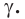 Плоскость
Плоскость 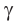 проходит и через прямую
проходит и через прямую 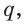 так как две точки
так как две точки 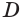 и
и 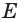 прямой
прямой 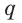 принадлежат плоскости
принадлежат плоскости 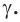
Допустим, что через прямые 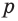 и
и 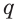 проходит ещё одна плоскость
проходит ещё одна плоскость 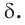 Тогда плоскость
Тогда плоскость 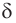 проходит через точку
проходит через точку 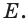 Но через эту точку и прямую
Но через эту точку и прямую 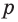 в соответствии с теоремой 3 проходит единственная плоскость. Значит, плоскость
в соответствии с теоремой 3 проходит единственная плоскость. Значит, плоскость 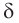 совпадает с плоскостью
совпадает с плоскостью  Таким образом, через пересекающиеся прямые
Таким образом, через пересекающиеся прямые 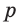 и
и 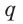 проходит единственная плоскость.
проходит единственная плоскость.
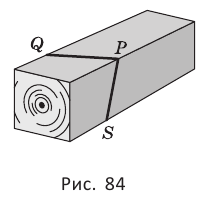
Теорема 4 находит своё применение на практике. Если столяру нужно распилить брусок под определённым углом, он, чтобы наметить плоскость распила, проводит в двух смежных гранях бруска пересекающиеся прямые 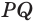 и
и 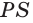 (рис. 84).
(рис. 84).
Пример №2
Докажите, что:
а) если некоторая точка 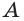 лежит на прямой
лежит на прямой 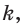 принадлежащей плоскости
принадлежащей плоскости 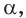 то точка
то точка 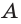 принадлежит плоскости
принадлежит плоскости 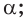
б) если две точки 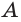 и
и 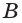 принадлежат как прямой
принадлежат как прямой 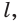 так и плоскости
так и плоскости 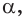 то прямая
то прямая 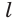 лежит в плоскости
лежит в плоскости 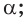
в) если плоскости 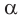 и
и 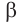 пересекаются по прямой
пересекаются по прямой 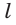 и точка
и точка 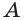 принадлежит как плоскости
принадлежит как плоскости 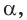 так и плоскости
так и плоскости 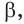 то точка
то точка 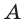 принадлежит прямой
принадлежит прямой 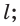
г) прямая 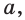 пересекающая в различных точках две пересекающиеся прямые
пересекающая в различных точках две пересекающиеся прямые 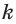 и
и 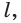 принадлежит плоскости этих прямых.
принадлежит плоскости этих прямых.
Решение:
a) 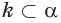 означает, что любая точка прямой
означает, что любая точка прямой 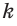 принадлежит также и плоскости
принадлежит также и плоскости 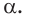
Любая точка прямой 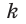 принадлежит плоскости
принадлежит плоскости 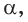 поэтому и некоторая точка
поэтому и некоторая точка 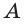 прямой
прямой 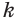 принадлежит плоскости а.
принадлежит плоскости а.
б) 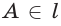 и
и 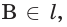 поэтому прямые
поэтому прямые 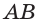 и
и 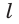 совпадают
совпадают 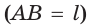 (аксиома прямой).
(аксиома прямой).
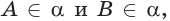 поэтому
поэтому 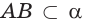 (аксиома 2).
(аксиома 2).
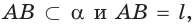 поэтому
поэтому 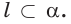
в) 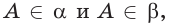 поэтому
поэтому 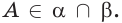
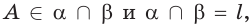 поэтому
поэтому 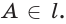
г) 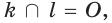 поэтому существует такая плоскость
поэтому существует такая плоскость 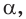 что
что 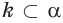 и
и 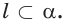
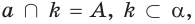 поэтому
поэтому 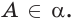
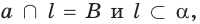 поэтому
поэтому 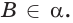
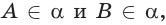 поэтому
поэтому 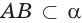 (аксиома 2).
(аксиома 2).
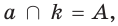 поэтому
поэтому 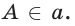
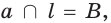 поэтому
поэтому 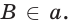
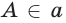 и
и 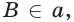 поэтому
поэтому 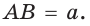
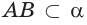 и
и 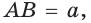 поэтому
поэтому 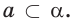
Пример №3
Основанием прямоугольного параллелепипеда 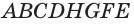 является квадрат
является квадрат 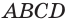 со стороной 6 см, а боковое ребро
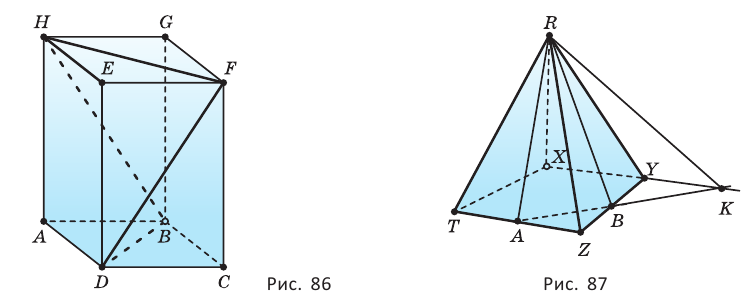
со стороной 6 см, а боковое ребро  параллелепипеда равно 8 см (рис. 86). Найдите длину пространственной ломаной
параллелепипеда равно 8 см (рис. 86). Найдите длину пространственной ломаной 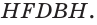
Решение:
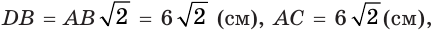 так как
так как 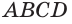 — квадрат.
— квадрат.
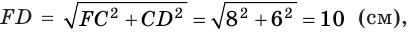
так как 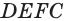 — прямоугольник.
— прямоугольник. 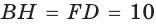 см, так как равные прямоугольники имеют равные диагонали.
см, так как равные прямоугольники имеют равные диагонали.
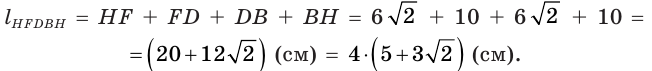
Ответ: 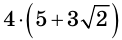 см.
см.
Пример №4
Точки 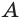 и
и 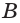 — середины рёбер
— середины рёбер 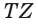 и
и 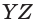 пирамиды
пирамиды 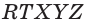 (рис. 87). Постройте:
(рис. 87). Постройте:
а) точку пересечения прямой 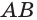 и плоскости
и плоскости 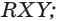
б) прямую, по которой пересекаются плоскости 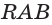 и
и 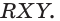
Решение:
а) 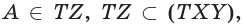 поэтому
поэтому 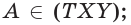
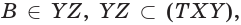 поэтому
поэтому 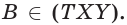
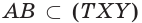 (аксиома 2).
(аксиома 2).
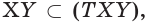 поэтому
поэтому 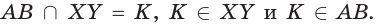
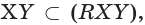 поэтому
поэтому 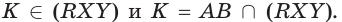
б) 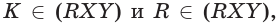 поэтому
поэтому 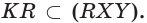
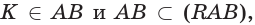 поэтому
поэтому 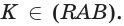
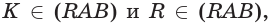 поэтому
поэтому 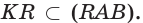
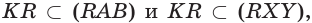 поэтому
поэтому 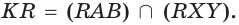
Пример №5
Точки 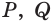 и
и 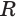 принадлежат соответственно рёбрам
принадлежат соответственно рёбрам 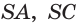 и
и 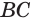 пирамиды
пирамиды 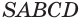 (рис. 88). Постройте прямую, по которой плоскость
(рис. 88). Постройте прямую, по которой плоскость 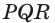 пересекает плоскость
пересекает плоскость 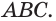
Решение:
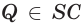 и
и 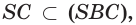 поэтому
поэтому 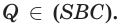
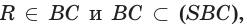 поэтому
поэтому 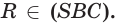
По аксиоме 2 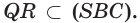
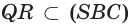 и
и 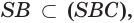
поэтому 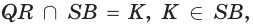
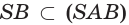 и
и 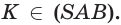
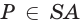 и
и 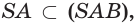 поэтому
поэтому 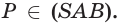
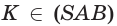 и
и 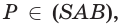 поэтому
поэтому 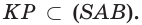
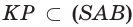 и
и 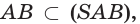
поэтому 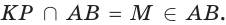
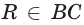 и
и 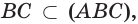 поэтому
поэтому 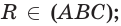
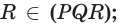 тогда
тогда 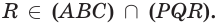
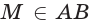 и
и 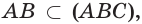 поэтому
поэтому 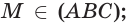
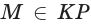 и
и 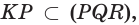 поэтому
поэтому 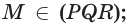
тогда 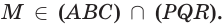
По аксиоме 3 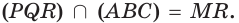
Пространственное моделирование
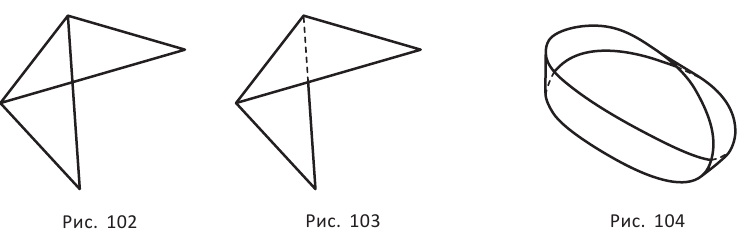
Ответьте, какая — плоская или пространственная — фигура изображена на рисунке:
а) 102; б) 103; в) 104.
На рисунке 104 изображена поверхность, которую называют лентой Мёбиуса, или листом Мёбиуса. Её открыли независимо друг от друга в 1858 году немецкие математики Август Мёбиус и Иоганн Листинг. До этого считалось, что любая поверхность имеет две стороны, которые можно окрасить в разный цвет.
Лента Мёбиуса имеет одну сторону и один край. В этом легко убедиться. Возьмём прямоугольную ленту 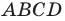 и склеим её так, чтобы точка
и склеим её так, чтобы точка 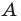 совпала с точкой
совпала с точкой 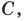 а точка
а точка 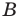 — с точкой
— с точкой 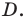 Сделайте это сами и попробуйте покрасить полученную ленту, не переходя через её край. Какой результат у вас получился?
Сделайте это сами и попробуйте покрасить полученную ленту, не переходя через её край. Какой результат у вас получился?
Какая поверхность получится, если лист Мёбиуса разрезать по его средней линии? Попробуйте окрасить эту поверхность. Что получилось? А что будет, если лист Мёбиуса разрезать, отступив от его края на третью часть ширины?
Памятный знак «Лист Мёбиуса» (рис. 105) был установлен 22 января 2009 года к 80-летию Национальной академии наук Беларуси.

Свойства ленты Мёбиуса нашли практическое применение и в промышленности. В виде ленты Мёбиуса изготавливают шлифовальные ленты, красящую ленту матричных принтеров, полосу ленточного конвейера, что позволяет увеличить срок службы, потому что вся поверхность ленты равномерно изнашивается. Ленту Мёбиуса применяют в системах записи на непрерывную плёнку, чтобы удвоить время записи.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |