Прямоугольник и его свойства с определением и примерами решения

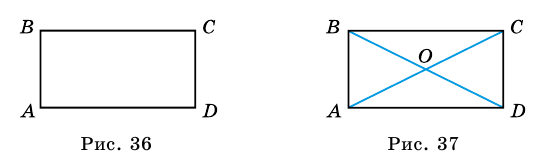
Прямоугольником называют параллелограмм, у которого все углы прямые (рис. 36).

Так как прямоугольник является параллелограммом, то он имеет все свойства параллелограмма.

1. В прямоугольнике противолежащие стороны равны.

2. Периметр прямоугольника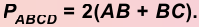

3. Диагонали прямоугольника точкой пересечения делятся пополам.

Кроме этих, прямоугольник имеет еще свойства.

4. Диагонали прямоугольника равны.

Доказательство:

Пусть дан прямоугольник 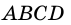(рис. 37). 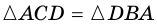(по двум катетам). Поэтому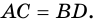 

5. Точка пересечения диагоналей прямоугольника равноудалена от всех его вершин.

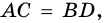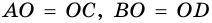Так как а (рис. 37), то, очевидно, что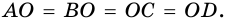

Пример:

Диагональ делит угол прямоугольника в отношении 2:3. Найдите угол между диагоналями этого прямоугольника.

Решение:

1) Пусть 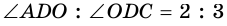(рис. 37). Обозначим 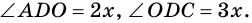Получим уравнение: 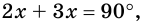откуда 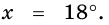Следовательно,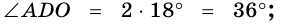

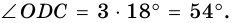
2) Найдем 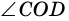 - угол между диагоналями данного прямоугольника. 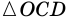- равнобедренный (так как 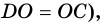поэтому 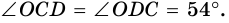В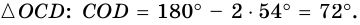

Ответ. 72°.

Рассмотрим признаки прямоугольника.

Теорема (признаки прямоугольника). Если у параллелограмма: 1) все углы равны, или 2) один угол прямой, или 3) диагонали равны, — то параллелограмм является прямоугольником.

Доказательство:

1) Так как все углы параллелограмма равны, а их сумма - 360°, то каждый из них равен 360° : 4 = 90°. А значит параллелограмм является прямоугольником.

2) Пусть угол 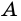параллелограмма 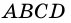- прямой (рис. 36). Тогда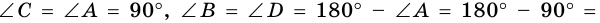 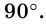Следовательно, все углы параллелограмма прямые, а значит он является прямоугольником.

3) Пусть у параллелограмма 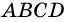диагонал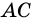и и 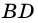равны (рис. 37). 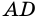- общая сторона треугольников 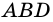и 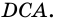Следовательно 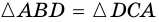(по трем сторонам), откуда 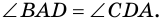Но 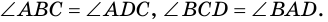Получаем, что у параллелограмма все углы равны, а значит он является прямоугольником (по п. 1 этой теоремы). 

Пример:

В окружности с центром 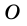проведены диаметры  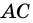и 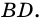Определите вид четырехугольника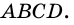

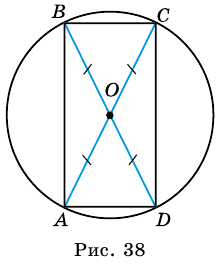
Решение:

1) Рассмотрим рис. 38. Так как 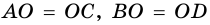(как радиусы), то, по признаку параллелограмма, 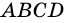- параллелограмм.

2) Так как 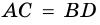(как диаметры), то, по признаку прямоугольника, получаем, что параллелограмм 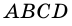-прямоугольник.

Ответ. Прямоугольник.