
Прямолинейное равноускоренное движение в физике - формулы и определения с примерами
Содержание:
Прямолинейное равноускоренное движение:
Движение с изменяющейся скоростью называют неравномерным. Простейшим видом неравномерного движения является прямолинейное движение с постоянным ускорением, т. е. прямолинейное равноускоренное движение. Впервые такое движение выделил и исследовал Галилей.
Равноускоренным называется движение, при котором скорость тела (МТ) за любые равные промежутки времени изменяется одинаково.
Ускорением 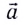

В СИ основной единицей ускорения является метр в секунду за секунду 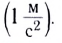
При прямолинейном равноускоренном движении ускорение 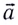 равно отношению изменения скорости
равно отношению изменения скорости 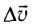 к промежутку времени
к промежутку времени 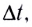 за который это изменение произошло:
за который это изменение произошло:

где 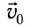 — начальная скорость (в момент времени
— начальная скорость (в момент времени 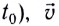 — скорость в момент времени t.
— скорость в момент времени t.
При таком движении ускорение 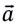 тела (МТ) всегда равно ее среднему ускорению:
тела (МТ) всегда равно ее среднему ускорению:
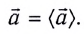
Кинематические уравнения равноускоренного движения имеют вид: 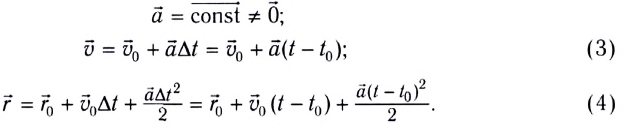
При прямолинейном равноускоренном движении тела (МТ) вдоль оси Ох зависимость координаты от времени выражается уравнением
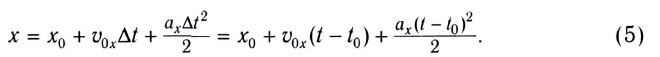
Если 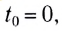 уравнения (3), (5) принимают вид:
уравнения (3), (5) принимают вид:
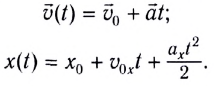
Поскольку ускорение при прямолинейном равноускоренном движении постоянно 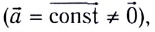 то график зависимости проекции ускорения от времени
то график зависимости проекции ускорения от времени 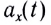 представляет собой отрезок прямой линии, параллельной оси времени Ot (рис. 16).
представляет собой отрезок прямой линии, параллельной оси времени Ot (рис. 16).

В случае, когда проекция ускорения положительна 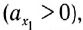 отрезок прямой проходит выше оси времени (график 1 на рисунке 16). В противном случае
отрезок прямой проходит выше оси времени (график 1 на рисунке 16). В противном случае 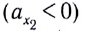 отрезок прямой проходит ниже оси времени (график 2 на рисунке 16).
отрезок прямой проходит ниже оси времени (график 2 на рисунке 16).
График зависимости проекции скорости от времени 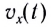 представляет собой линейную функцию (рис. 17). Тангенс угла наклона (tga) этой прямой численно равен проекции ускорения
представляет собой линейную функцию (рис. 17). Тангенс угла наклона (tga) этой прямой численно равен проекции ускорения 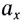 движения:
движения:
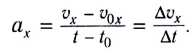
Если проекция скорости на выбранную ось Ох положительна 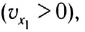 то угол
то угол 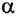 — острый (угол
— острый (угол 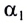 на рисунке 17), а если отрицательна
на рисунке 17), а если отрицательна 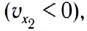 — тупой (угол
— тупой (угол 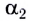 на рисунке 17).
на рисунке 17).
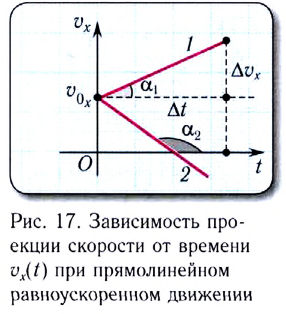
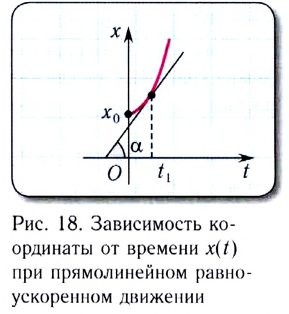
График зависимости координаты от времени x(t) при прямолинейном равноускоренном движении представляет собой ветвь параболы (рис. 18). Проекция скорости 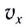 тела в момент времени
тела в момент времени 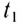 численно равна тангенсу угла наклона tga касательной к оси абсцисс.
численно равна тангенсу угла наклона tga касательной к оси абсцисс.
Подчеркнем, что в процессе движения путь, пройденный материальной точкой, все время увеличивается, в то время как проекция перемещения (координата) может уменьшаться. Вследствие этого график зависимости пути от времени s(t) будет совпадать с графиком зависимости координаты от времени х(t) (рис. 19) на тех участках, где координата увеличивается (см. участок от начала координат до точки В на рисунке).
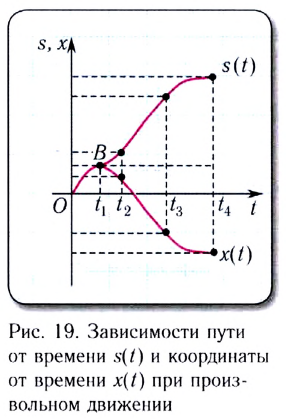
Соответственно, на тех участках, где координата уменьшается, график зависимости пути от времени является «зеркальным» отражением кривой х(t) от горизонтальной плоскости, проходящей через точку, с которой началось уменьшение координаты (см. точку В на рисунке).
Так как зависимость проекции скорости прямолинейного движения тела вдоль оси Ох от времени 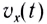 является линейной функцией, то проекция средней скорости
является линейной функцией, то проекция средней скорости 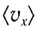 движения тела при прямолинейном равноускоренном движении равна среднему арифметическому его начальной и конечной проекций скоростей:
движения тела при прямолинейном равноускоренном движении равна среднему арифметическому его начальной и конечной проекций скоростей:
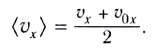
Соответственно, в этом случае проекция перемещения на ось Ох (путь)
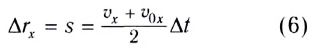
численно равна площади закрашенной трапеции (рис. 20).
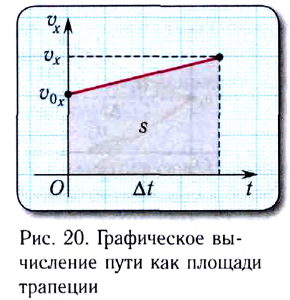
Исключая время t из уравнений прямолинейного равноускоренного движения для скорости v(t) и координаты x(t), можно получить еще одну часто используемую формулу
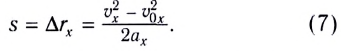
Прибор для измерения ускорения называется акселерометром.
Примером равноускоренного прямолинейного движения является свободное падение тел, при котором на тело действует только сила тяжести, и оно движется с ускорением 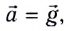 где
где 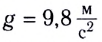 — ускорение свободного падения.
— ускорение свободного падения.
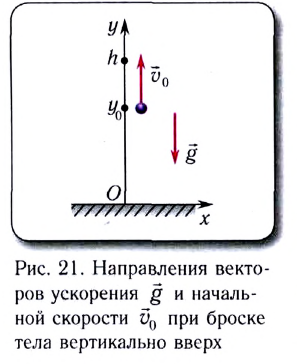
Если ось Оу направлена вертикально вверх, а ось Ох — вдоль поверхности Земли (рис. 21), то движение тела (МТ), брошенного вертикально вверх со скоростью 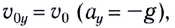 описывается формулами:
описывается формулами:
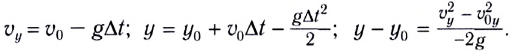
В случае, когда 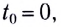 зависимости проекции скорости и координаты от времени принимают соответственно вид:
зависимости проекции скорости и координаты от времени принимают соответственно вид:
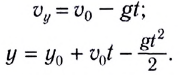
Время подъема тела (МТ) на максимальную высоту, на которой 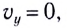 можно
можно 
Скорость в момент возвращения тела (МТ) в исходную точку О определяется по формуле 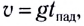 и она равна начальной скорости
и она равна начальной скорости 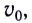 так как время подъема тела (МТ) равно времени его падения
так как время подъема тела (МТ) равно времени его падения 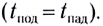
Докажите самостоятельно, что без учета сопротивления воздуха время подъема тела (МТ) равно времени его падения.
Высоту подъема h тела (МТ) (см. рис. 21) за промежуток времени 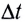 можно определить из соотношения
можно определить из соотношения 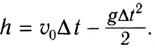
Максимальная высота подъема тела (МТ) определяется по формуле

Модуль скорости на высоте h (см. рис. 21) можно найти ио формуле

При движении тела (МТ) из начальной точки 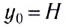 с начальной скоростью
с начальной скоростью 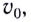 направленной вертикально вниз (рис. 22), его скорость в произвольный момент времени
направленной вертикально вниз (рис. 22), его скорость в произвольный момент времени 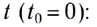
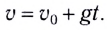
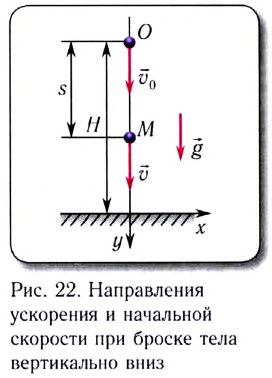
Пройденный телом (МТ) путь s определяется по формуле
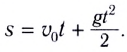
Скорость в конце пути s: 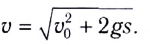
Падение тел с высоты Н без начальной скорости 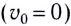 представляет собой частный случай прямолинейного равноускоренного движения. При выборе оси Оу, направленной вертикально вниз
представляет собой частный случай прямолинейного равноускоренного движения. При выборе оси Оу, направленной вертикально вниз 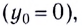 скорость в любой момент времена находится из соотношения
скорость в любой момент времена находится из соотношения 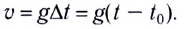
При 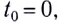 то скорость v = gt.
то скорость v = gt.
Координата у и пройденный путь s определяются соответственно по формулам: 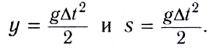
Продолжительность свободного падения с высоты Н:

Скорость тела при свободном падении с высоты Н:

Равноускоренное движение
Прямолинейное равномерное движение, то есть движение с постоянной скоростью, -редкое явление в окружающей среде. Значительно чаще придется иметь дело с такими движениями, в которых скорость не является постоянной, а со временем изменяется. Такие движения называют неравномерными.
На всех современных транспортных средствах устанавливают специальные приборы -спидометры (рис. 266), показывающие значение скорости в данный момент времени.

Понятно, что по спидометру нельзя определить направление скорости. Для некоторых средств транспорта, например для морских кораблей и самолетов, необходимо знать также направление скорости движения. Тогда, кроме спидометра, устанавливают еще и другие навигационные приборы, в самом простом случае - компас.
Следовательно, теперь мы знаем, что при неравномерном движении скорость движения тела не является постоянной величиной и в разные моменты времени имеет свое направление и значение.
Для упрощения будем рассматривать такое неравномерное движение, при котором скорость движения тела за каждую единицу времени и вообще за любые равные интервалы времени изменяется одинаково. Такое движение называют равноускоренным.
Движение тела, при котором его скорость за любые равные интервалы времени изменяется одинаково, называют равноускоренным движением.
Во время такого движения скорость может изменяться.
Если за некоторый интервал времени 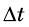 приращение скорости равен
приращение скорости равен 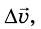 то за удвоенный интервал времени
то за удвоенный интервал времени 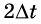 приращение скорости будет удвоенным -
приращение скорости будет удвоенным -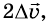 за утроенный интервал времени З
за утроенный интервал времени З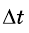 он будет утроенным -
он будет утроенным -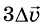 и т. д.
и т. д.
При этом если значение 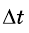 изменить, то новому
изменить, то новому 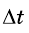 будет соответствовать уже другое значение
будет соответствовать уже другое значение 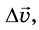 , но отношение
, но отношение 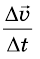 приращения скорости к
приращения скорости к
приращению времени будет таким же, как и раньше. Следовательно, в
данном равноускоренном прямолинейном движении отношение 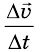 неизменно, инвариантно относительно выбора интервала времени At.
неизменно, инвариантно относительно выбора интервала времени At.
Вектор 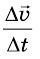 , который является постоянным для каждого данного прямолинейного равноускоренного движения, характеризует изменение скорости тела за единицу времени. Эта векторная величина - основная характеристика равноускоренного движения, которую называют ускорением и обозначают буквой
, который является постоянным для каждого данного прямолинейного равноускоренного движения, характеризует изменение скорости тела за единицу времени. Эта векторная величина - основная характеристика равноускоренного движения, которую называют ускорением и обозначают буквой 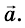
Ускорением тела в его равноускоренном прямолинейном движении называют векторную физическую величину, характеризующую изменение скорости за единицу времени и равную отношению изменения скорости движения тела к интервалу времени, за которое это изменение произошло:
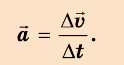
Из определения равноускоренного движения следует, что его ускорение является постоянной величиной 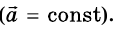
Если в выбранный начальный момент времени t = 0 скорость движения тела равна 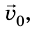 , а в момент времени t -
, а в момент времени t - 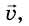 , то имеем
, то имеем 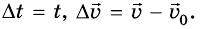 Тогда рассмотренная выше формула имеет вид:
Тогда рассмотренная выше формула имеет вид:
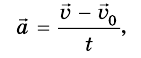
где 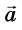 - ускорение движения тела;
- ускорение движения тела; 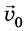 - начальная скорость движения тела;
- начальная скорость движения тела; 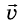 - его конечная скорость движения; t - время, за которое это изменение происходило.
- его конечная скорость движения; t - время, за которое это изменение происходило.
Как видно из этой формулы, за единицу ускорения следует взять ускорение такого прямолинейного равноускоренного движения, при котором за единицу времени скорость изменяется также на единицу. И это означает: ускорение равно единице, если за 1 с скорость движения тела изменяется на 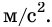 Следовательно, единицей ускорения в СИ является 1 м/с2.
Следовательно, единицей ускорения в СИ является 1 м/с2.
Равноускоренное движение может быть ускоренным или замедленным. Рассмотрим ускорение и скорость равноускоренного движения в проекциях на ось Ох (рис. 267), тогда ускорение будет приобретать вид: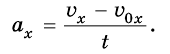
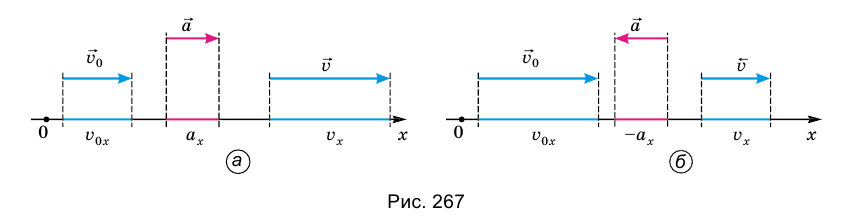
Если 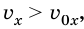 то есть скорость движения тела увеличивается (рис. 267, а), тогда модуль ускорения
то есть скорость движения тела увеличивается (рис. 267, а), тогда модуль ускорения 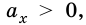 а его вектор совпадает с направлением движения, то это движение называют равноускоренным.
а его вектор совпадает с направлением движения, то это движение называют равноускоренным.
Если 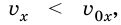 тогда модуль ускорения
тогда модуль ускорения 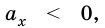 а его вектор противоположный по направлению движения, то такое движение называют равнозамедленным.
а его вектор противоположный по направлению движения, то такое движение называют равнозамедленным.
Вам уже известно, как графически изображается равномерное прямолинейное движение тела. Попробуем аналогично представить графически равноускоренное прямолинейное движение.
Графики равномерного прямолинейного движения тела
Рассмотрим график проекции ускорения движения тела 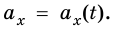 Если вспомнить график проекции скорости тела в равномерном прямолинейном движении, где v = const, и сравнить его со случаем, когда
Если вспомнить график проекции скорости тела в равномерном прямолинейном движении, где v = const, и сравнить его со случаем, когда 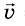 = const, то становится понятно, что эти графики идентичны. Поэтому графиком зависимости проекции ускорения движения тела от времени будет тоже прямая, параллельная оси времени t. В зависимости от значения проекции ускорения - положительная она или отрицательная -прямая расположена или над осью, или под ней (рис. 268).
= const, то становится понятно, что эти графики идентичны. Поэтому графиком зависимости проекции ускорения движения тела от времени будет тоже прямая, параллельная оси времени t. В зависимости от значения проекции ускорения - положительная она или отрицательная -прямая расположена или над осью, или под ней (рис. 268).
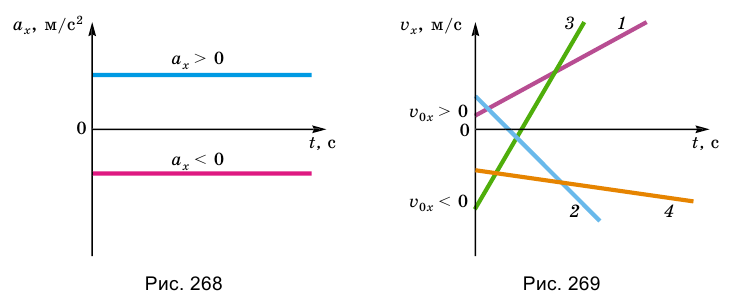
График проекции скорости движения тела 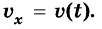 Из кинематического уравнения
Из кинематического уравнения 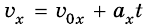 видно, что зависимость проекции скорости движения тела от времени является линейной, как и в уравнении равномерного прямолинейного движения. Тогда остается только проанализировать его для нашего случая. В зависимости от значений проекций ускорения
видно, что зависимость проекции скорости движения тела от времени является линейной, как и в уравнении равномерного прямолинейного движения. Тогда остается только проанализировать его для нашего случая. В зависимости от значений проекций ускорения 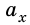 и начальной скорости движения тела
и начальной скорости движения тела 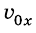 график будет иметь разный вид (рис. 269), в частности:
график будет иметь разный вид (рис. 269), в частности:
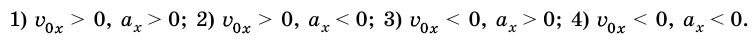
Если 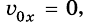 то прямая будет выходить с начала координат и, в зависимости от значения проекции ускорения движения тела, будет направлена вверх
то прямая будет выходить с начала координат и, в зависимости от значения проекции ускорения движения тела, будет направлена вверх 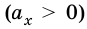 или вниз
или вниз 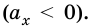 Наклон прямых зависит от значения проекции ускорения: чем больше ускорение движения тела, тем круче подымается или убывает график.
Наклон прямых зависит от значения проекции ускорения: чем больше ускорение движения тела, тем круче подымается или убывает график.
График движения тела х = x(t). Кинематические уравнения движения являются квадратичной функцией вида 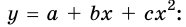
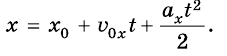
Поэтому графиком зависимости координаты тела от времени является парабола, ветви которой согласно параметрам движения имеют разное направление. Например, если 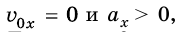 то график имеет вид, изображенный на рисунке 270, а. Если
то график имеет вид, изображенный на рисунке 270, а. Если 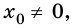 то вершина параболы смещается по оси ординат вверх или вниз, в зависимости от значения
то вершина параболы смещается по оси ординат вверх или вниз, в зависимости от значения 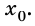
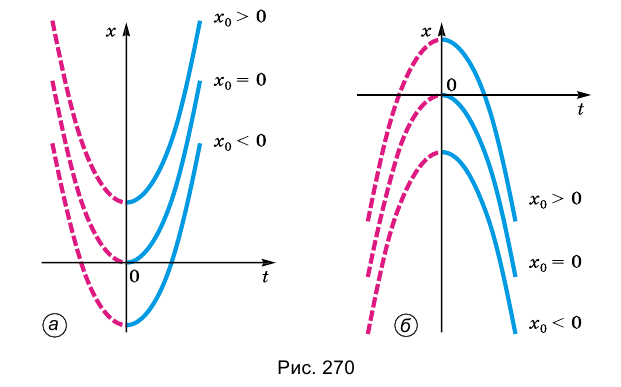
Если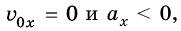 то ветви параболы направлены вниз (рис. 270, б) и смещение вершины параболы вверх или вниз по оси ординат также зависит от значения
то ветви параболы направлены вниз (рис. 270, б) и смещение вершины параболы вверх или вниз по оси ординат также зависит от значения 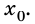
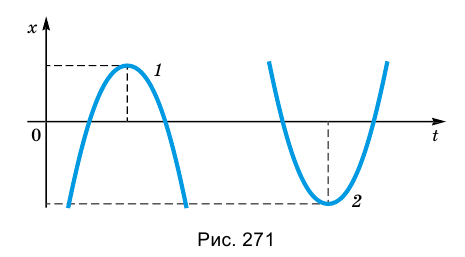
Если 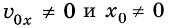 (рис. 271), то вершина параболы смещается в точку, координаты которой определяются соотношениями:
(рис. 271), то вершина параболы смещается в точку, координаты которой определяются соотношениями:
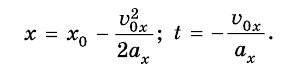
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |