Прямая в пространстве и ее изображение на чертеже с примерами

Содержание:

Задание прямой в пространстве:

Любая прямая в пространстве может быть задана: 

• двумя точками, принадлежащими этой прямой; 
• одной точкой, принадлежащей данной прямой, и ее направлением. 

В  первом  случае  задаются  координаты  двух  заданных  точек,  во втором — координаты  точки и направляющим вектором. 

Положение прямой в пространстве 

Положение прямой в пространстве оценивается расположением ее относительно трех  плоскостей  проекций.  При  этом  возможны  следующие варианты. 

Прямая не параллельная и не перпендикулярная ни  к одной из плоскостей проекций называется прямой общего положения (рис.4.1). 

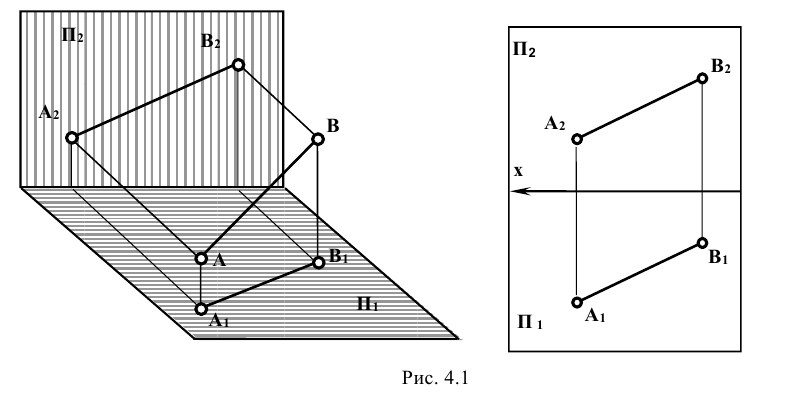
Все  точки  прямой  имеют  различные  координаты  х,  у,  z,  и  ее проекции не параллельны и не перпендикулярны осям проекций х, у, z. 

Прямая  параллельная  одной  из  плоскостей  проекций.  Все точки прямой имеют одну постоянную координату x, y или z. При этом одна из проекций прямой параллельна какой-то оси проекции. Такую прямую называют линией уровня (рис. 4.2). 

На рис. 4.2, а прямая h (горизонталь) параллельна плоскости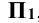 

На рисунке 4.2, б прямая f (фронталь)   параллельна плоскости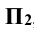, ее горизонтальная проекция 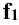параллельна оси  x:, координата у для  всех  точек постоянна,    фронтальная  проекция  прямой  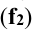проецируется в натуральную величину. 

На рисунке 4.2, в прямая р параллельна плоскости П3, в этом случае  ее горизонтальная  проекция 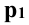 параллельна  оси  у,  фронтальная проекция  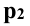 параллельна  оси  z,  координата  x  для  всех  точек  прямой постоянна,  а профильная  проекция  прямой  проекция  прямой  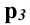 проецируется в натуральную величину.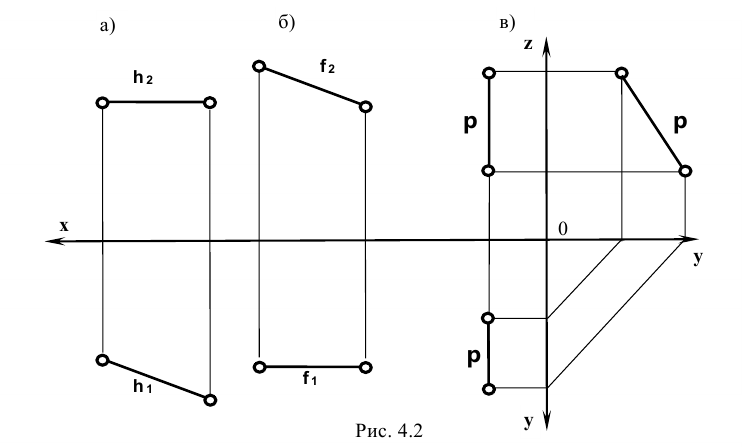 

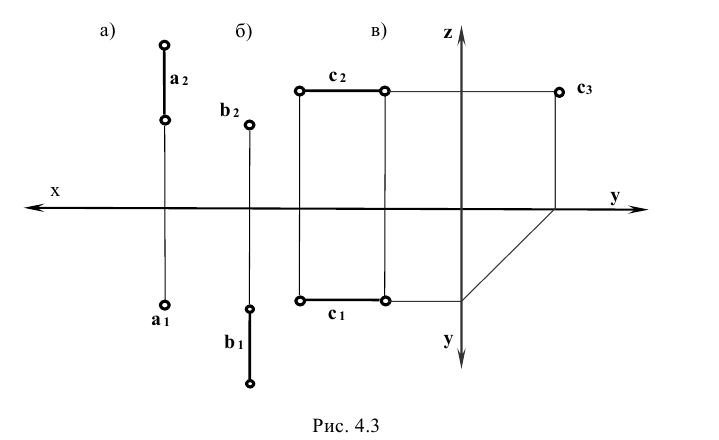
Прямая перпендикулярна к одной из плоскостей проекций и  параллельна  двум  другим  плоскостям  проекций.  Если  все  точки прямой имеют две постоянные координаты то на одну из плоскостей проекций  прямая проецируется  в  точку.  Такую  прямую  называют проецирующей прямой (рис. 4.3). 

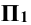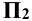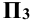На  рис.  4.3,  а  прямая  а  перпендикулярна  к  плоскости  И параллельна плоскостям и . Координаты x и у всех точек прямой постоянны.  На горизонтальную  плоскость  проекции  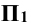прямая  а проецируется в точку (горизонтально-проецирующая прямая). 

На рис. 4.3, б прямая b перпендикулярна к плоскости проекции П2  и параллельна плоскостям 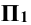и 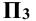. Координаты х и z всех точек постоянны. На фронтальную плоскость 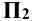прямая b проецируется в точку (фронтально-проецирующая прямая). 

На рис. 4.3, в прямая с перпендикулярна к плоскости проекции 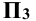 и параллельна плоскостям 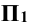и 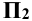.  Координаты  у и z  всех  точек прямой постоянны.  На  профильную  плоскость  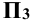  прямая  с проецируется в точку (профильно-проецирующая прямая). 

Принадлежность точки прямой 

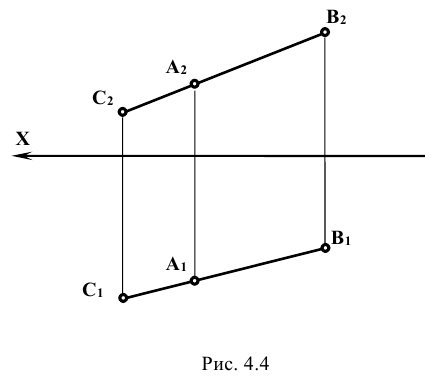
Признаком  принадлежности  точки  некоторой  прямой  является  принадлежность  проекций  точки  одноименным  проекциям  этой прямой. Так на рис. 4.4 точка А принадлежит отрезку прямой СВ, так как  проекции  точки  А  расположены  на одноименных  проекциях отрезка  прямой  СВ                                      ().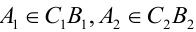 

 

Следы прямой 

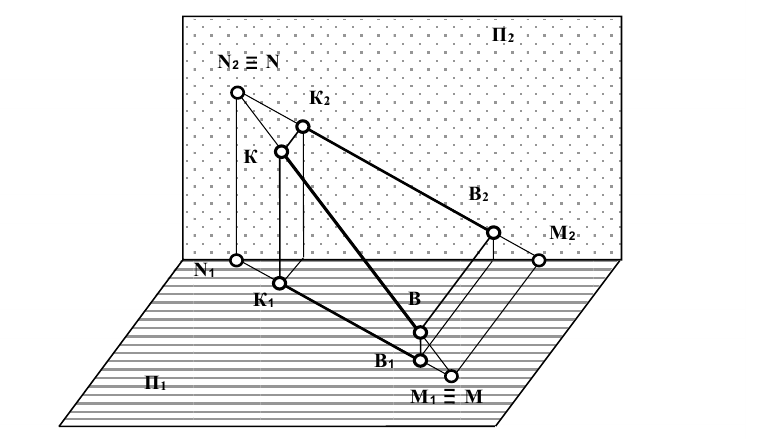
Следом  прямой называется  точка пересечения  прямой  с плоскостью проекции. Горизонтальным  следом прямой  называют  точку пересечения прямой с горизонтальной плоскостью проекций (рис. 4.5). Горизонтальный  след обозначают  обычно  буквой  М.  При  этом у координата  z  точки  М  равна  нулю. Следовательно,  для  нахождения горизонтального  следа  прямой  на  ней определяют  точку  с  нулевой координатой z (рис. 4.5). 

Фронтальным  следом  прямой  называют  точку  пересечения прямой  с фронтальной  плоскостью  проекции  (рис.  4.5).  Обозначают фронтальный след чаще всего буквой N. Координата у точки N равна нулю. Следовательно, для нахождения фронтального следа N прямой на ней определяют точку, имеющую нулевую координату у. Профильным  следом  прямой  называют  точку пересечения прямой с профильной плоскостью проекции. Обозначают профильный след обычно буквой Р. Координата х точки Р равна нулю.

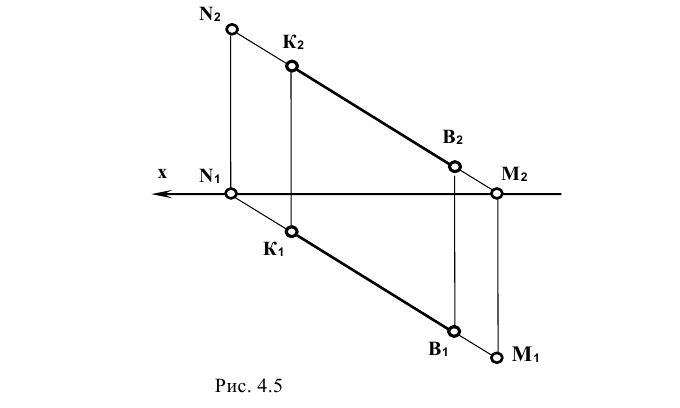
Пересекая  плоскости  проекции,  прямая  переходит  из  одной четверти (квадранта) пространства в другую. Линия общего положения и линия уровня может пройти через три четверти пространства; линия уровня и проецирующая линия — через две четверти. 

• Заказать чертежи

Длина отрезка прямой и углы наклона прямой к плоскостям проекции. Способ прямоугольного треугольника  

Отрезок прямой, параллельной какой-либо плоскости проекции, проецируется на данную  плоскость  без  искажения  (в  натуральную величину) (рис. 4.6, а и 4.6, б). 

Так, отрезок АВ параллелен плоскости 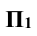(рис. 4.6, а), следовательно, длина отрезка равна его горизонтальной проекции 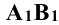. Угол β между осью х и горизонтальной проекцией отрезка определяет угол наклона отрезка АВ к плоскости. 

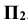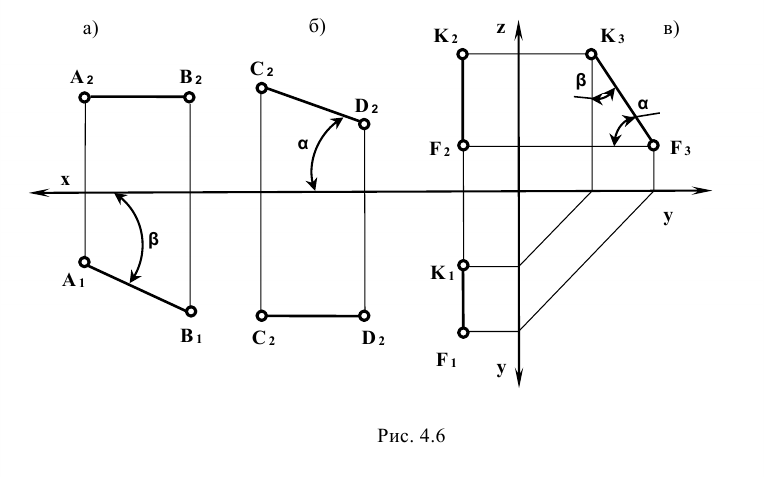
Отрезок  CD  параллелен  плоскости 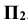  (рис.  4.6,  б), следовательно, длина отрезка равна длине его фронтальной проекции  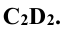Угол α  определяет угол наклона отрезка CD к плоскости . 

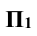Отрезок KF параллелен плоскости 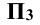(рис. 4.6, в), следовательно, длина  отрезка равна  длине  его  профильной  проекции  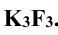.  Углы наклона  отрезка  к плоскостям  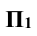 и 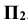   определяют  соответственно углы α и β. 

Если  отрезок  не  параллелен  плоскостям  проекций,  то  для определения его натуральной величины и угла наклона к плоскостям проекций  необходимо выполнить  дополнительные  построения: построить  вспомогательный прямоугольный  треугольник,  один катет которого равен проекции отрезка на плоскость 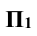или 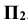, а другой - разности координат  концов отрезка с другой проекции.  

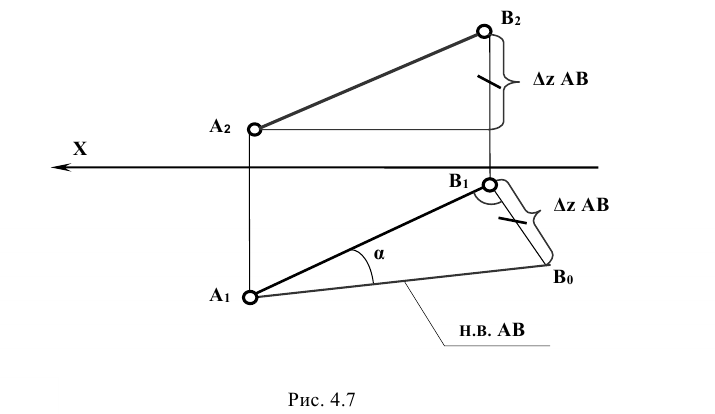
Так на рис. 4.7 один катет вспомогательного треугольника равен  горизонтальной  проекции  отрезка 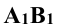  а  другой  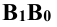–  -  разности  координат z концов  отрезка  (точек  А  и  В)  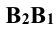.  Гипотенуза  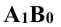  определяет действительную длину отрезка АВ. Угол α при вершине  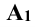 определяет угол наклона отрезка АВ к плоскости . 

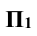Теорема о проецировании прямого угла

Для  того  чтобы  прямой  угол  проецировался    на  плоскость проекций  в натуральную  величину  необходимо  и  достаточно,  чтобы, по крайней мере, одна его сторона была параллельна этой плоскости проекции, а вторая сторона не перпендикулярна к ней.  

На рис. 4.8 дано: 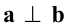; плоскость 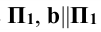. Доказать, что .

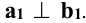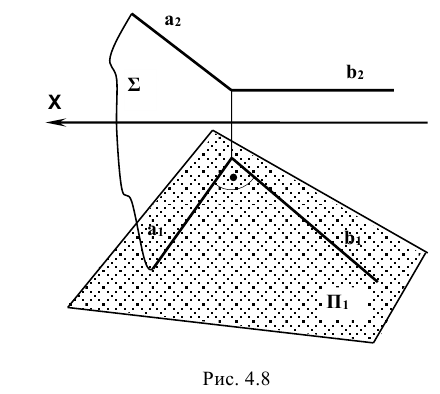
Для доказательства через прямую а (проекци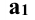и и 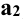) проводим дополнительную плоскость Σ. Прямая b перпендикулярна к плоскости Σ и параллельна плоскости 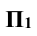. Плоскости 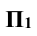принадлежит проекция прямой.

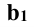Отсюда следует, что прямая 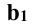тоже перпендикулярна к плоскости Σ. Прямая а принадлежит плоскости Σ, следовательно, 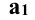перпендикулярна к 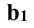, т.е. прямой угол проецируется без искажения.

Взаимное положение прямых в пространстве

Две прямые в пространстве могут быть параллельными, пересекающимися или скрещивающимися. Если две прямые пересекаются, то точки пересечения одноименных проекций лежат на линии проекционной связи (рис. 4.9, а).

Если две прямые параллельны, то их одноименные проекции параллельны (рис. 4.9, б). Это утверждение справедливо, если прямые занимают общее положение.

Если две прямые не параллельны и не пересекаются, то есть не лежат в одной плоскости, то они являются скрещивающимися (рис. 4.9, в).

Взаимное положение двух прямых, в том случае, если одна из них является профильной прямой, устанавливается при помощи третьей проекции.

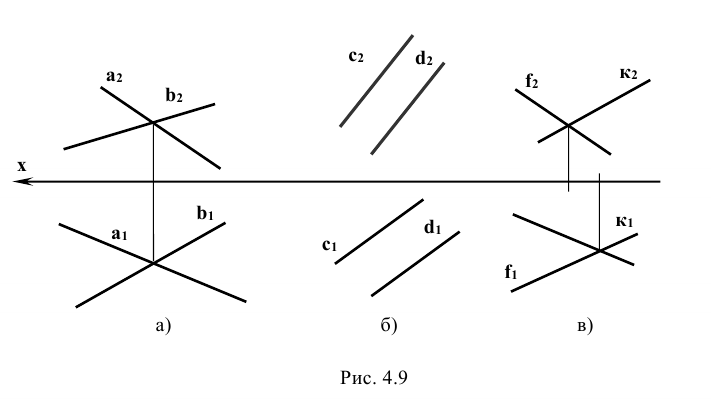
На рис. 4.10 изображены две скрещивающиеся прямые, хотя их горизонтальные и фронтальные проекции пересекаются, а профильные — параллельны между собой.

Рис. 4.10