Проверка гипотезы о равенстве вероятностей - определение и вычисление с примерами решения

Проверка гипотезы о равенстве вероятностей:

Пусть некоторое событие А в серии из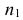 

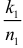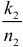Если частоты появления события и в этих серия не принимают значений близких к 0 или 1, то по центральной предельной теореме частоты имеют близкие к нормальному законы распределения: 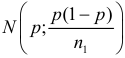и 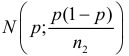соответственно. Поэтому в силу устойчивости нормального закона распределения разность частот 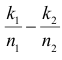имеет закон распределения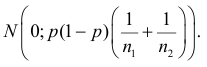

Заметим, что большие различия в частотах появления события свидетельствуют против гипотезы. Поэтому к критическим следует отнести те серии наблюдений, для которых 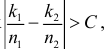где С – некоторая положительная постоянная. Если уровень значимости выбрать равным 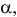то постоянная С определяется из равенства

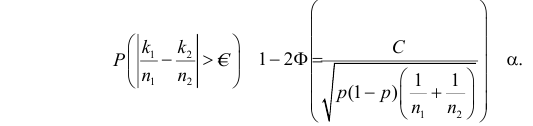
Если по таблице функции Лапласа (см. прил., табл. П2) найти 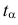такое, чтобы 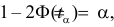то следует выбрать 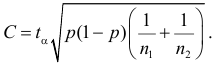К критическим следует отнести те серии наблюдений, в которых модуль разности частот больше величины 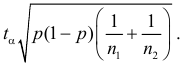В последнем равенстве в качестве оценки неизвестной вероятности 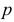можно взять величину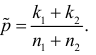

Пример:

В 225 независимых опытах событие A появилось 78 раз. В контрольной серии из 64 независимых опытов было зарегистрировано 12 появлений события. Можно ли считать, что вероятность события A одинакова в обеих сериях опытов при уровне значимости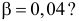

Решение. Предположим, что вероятности события в этих опытах одинаковы. По таблице функции Лапласа (см. прил., табл. П2) находим, что 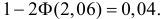Оценкой неизвестной вероятности в предположении, что гипотеза о равенстве вероятностей верна, может служить величина 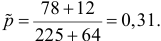Поэтому критическую область составят те серии опытов, в которых модуль разности частот превысит величину

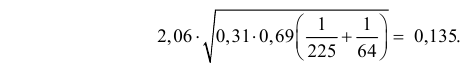
Реальная разность частот равна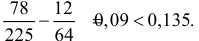

Предположение о равенстве вероятностей не противоречит опытным данным.

Ответ. Предположение о равенстве вероятностей правдоподобно.