
Пространственная система сил в теоретической механике
Содержание:
Пространственная система сил:
Изменение главного момента при перемене центра приведения
При перемене центра приведения векторные моменты сил изменяются, так как изменяются радиусы-векторы их точек приложения. Вследствие этого изменяется главный момент. Оценим изменение главного момента системы сил 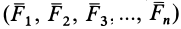
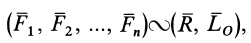
то для получения главного момента 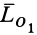 достаточно привести к новому центру систему
достаточно привести к новому центру систему 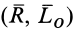 . Силу
. Силу 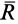 из точки
из точки 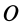 перенесем в точку
перенесем в точку 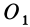 . Получим в этой точке силу
. Получим в этой точке силу 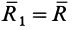 и, согласно теореме о параллельном пере носе силы, присоединенную пару сил с векторным моментом
и, согласно теореме о параллельном пере носе силы, присоединенную пару сил с векторным моментом 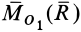 . Векторный момент пары сил
. Векторный момент пары сил 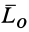 , вычисленный относительно точки
, вычисленный относительно точки 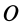 как вектор свободный, можно приложить в любой точке тела. Новый главный момент относительно точки
как вектор свободный, можно приложить в любой точке тела. Новый главный момент относительно точки 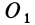 по правилу сложения пар сил является векторной суммой моментов
по правилу сложения пар сил является векторной суммой моментов 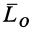 и
и 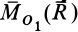 , т.е.
, т.е.
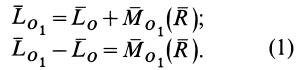
По формуле для векторного момента силы имеем
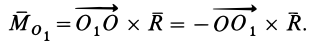
С учетом этого формула (1) примет вид
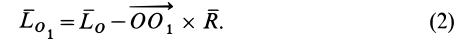
Итак, главный момент системы сил при перемене центра приведения изменяется на векторный момент главного вектора 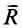 , приложенного в старом центре приведения, относительно нового центра приведения
, приложенного в старом центре приведения, относительно нового центра приведения 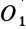 .
.
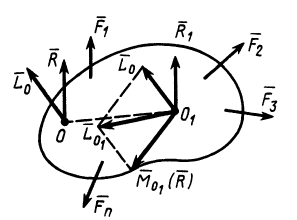
Рис. 71
Инварианты системы сил
Инвариантами в статике называются такие величины для рассматриваемой системы сил, которые не изменяются при изменении центра приведения. Одним из инвариантов является главный вектор, так как в любом центре приведения он выражается векторной суммой системы сил. Если в одном центре приведения 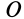 главный вектор
главный вектор 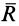 , а в другом
, а в другом 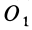 он
он 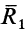 , то
, то

Таким образом, главный вектор системы сил является векторным инвариантом. Для одной и той же системы сил он не зависит от выбора центра приведения.
Из векторного равенства (3) следует, что равны модули и проекции главных векторов на любые оси координат, т. е.
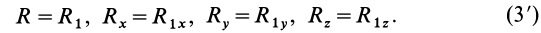
Для получения второго, скалярного, инварианта используем формулу (2):
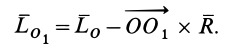
Умножая обе части этого равенства скалярно на 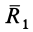 причем в правой части при умножении вместо
причем в правой части при умножении вместо 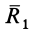 , согласно (3), возьмем
, согласно (3), возьмем 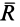 , получим
, получим
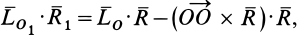
или
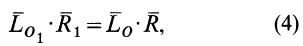
так как смешанное произведение векторов, содержащих два одинаковых множителя 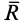 , равно нулю, т. е.
, равно нулю, т. е.
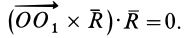
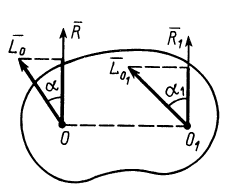
Рис. 72
Соотношение (4) является вторым скалярным инвариантом: скалярное произведение главного момента на главный вектор не зависит от центра приведения. Второй скалярный инвариант можно выразить в двух других эквивалентных формах, если раскрыть скалярное произведение векторов в (4). Обозначая проекции 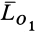 на оси координат через
на оси координат через 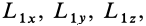 а проекции
а проекции 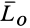 — соответственно через
— соответственно через 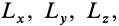 второй инвариант можно выразить в форме
второй инвариант можно выразить в форме
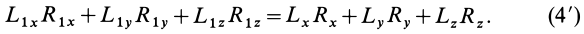
Кроме того, формуле (4) можно придать вид
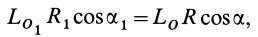
где 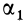 —угол между векторами
—угол между векторами 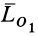 и
и 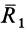 , а
, а 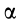 —между
—между 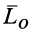 и
и 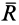 (рис. 72). После сокращения
(рис. 72). После сокращения 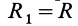 получим
получим

В этой форме второй инвариант утверждает, что проекция главного момента на направление главного вектора не зависит от центра приведения.
Если главный момент в каждом центре приведения разложить на две взаимно перпендикулярные составляющие, одна из которых направлена по главному вектору, то, учитывая, что главные векторы в различных центрах приведения параллельны, согласно (4"), получим

где 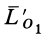 —составляющая главного момента
—составляющая главного момента 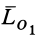 по направлению главного вектора
по направлению главного вектора 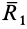 , а
, а 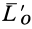 — составляющая главного момента
— составляющая главного момента 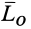 по направлению главного вектора
по направлению главного вектора 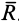 . Соотношение (5) является следствием первого и второго инвариантов.
. Соотношение (5) является следствием первого и второго инвариантов.
Рассмотренные инварианты (3) и (4) являются независимыми, т. е. из одного не следует другой. Комбинируя эти инварианты, можно получить другие, зависящие от них инварианты.
Частные случаи приведения пространственной системы сил
Произвольная система сил приводится к силе, равной главному вектору 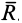 , и паре сил, векторный момент которой равен главному моменту
, и паре сил, векторный момент которой равен главному моменту 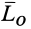 . В зависимости от их модулей и взаимного направления, т. е. угла
. В зависимости от их модулей и взаимного направления, т. е. угла 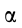 между ними, можно произвести дальнейшие упрощения.
между ними, можно произвести дальнейшие упрощения.
Приведение к паре сил
Если 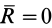 ,
, 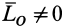 , то система сил приводится к одной паре сил, причем главный момент в этом случае, согласно (2), не зависит от выбора центра приведения. В рассматриваемом случае оба инварианта системы сил равны нулю, т. е.
, то система сил приводится к одной паре сил, причем главный момент в этом случае, согласно (2), не зависит от выбора центра приведения. В рассматриваемом случае оба инварианта системы сил равны нулю, т. е.
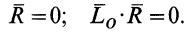
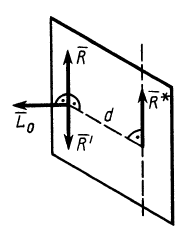
Рис. 73
Приведение к равнодействующей
Возможны два случая.
1. Если 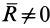 ,
, 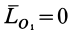 (первый инвариант
(первый инвариант 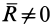 , второй-
, второй- 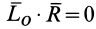 ), то система приводится к равнодействующей силе
), то система приводится к равнодействующей силе 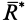 , равной по модулю и направлению главному вектору
, равной по модулю и направлению главному вектору 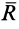 , т. е.
, т. е.
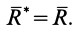
Линия действия равнодействующей силы в этом случае проходит через центр приведения.
2. Если 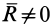 ,
, 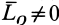 , но
, но 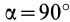 , т.е.
, т.е. 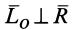 (первый инвариант
(первый инвариант 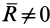 , второй —
, второй — 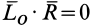 ), то система сил тоже приводится к равнодействующей, причем опять
), то система сил тоже приводится к равнодействующей, причем опять
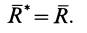
Но линия действия равнодействующей силы 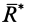 отстоит от центра приведения на расстоянии
отстоит от центра приведения на расстоянии 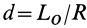 . Действительно, в этом случае имеем силу и пару сил с векторным моментом
. Действительно, в этом случае имеем силу и пару сил с векторным моментом 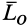 , причем силы пары можно считать расположенными в одной плоскости с силой
, причем силы пары можно считать расположенными в одной плоскости с силой 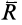 так как векторный момент пары перпендикулярен силе
так как векторный момент пары перпендикулярен силе 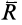 (рис. 73). Поворачивая и перемещая пару сил в ее плоскости, а также изменяя силы пары и ее плечо, при сохранении векторного момента можно получить одну из сил пары
(рис. 73). Поворачивая и перемещая пару сил в ее плоскости, а также изменяя силы пары и ее плечо, при сохранении векторного момента можно получить одну из сил пары 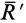 , равной по модулю, но противоположной по направлению главному вектору
, равной по модулю, но противоположной по направлению главному вектору 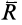 . Другая сила пары
. Другая сила пары 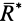 и будет равнодействующей силой. Действительно,
и будет равнодействующей силой. Действительно,
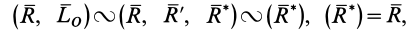
так как система двух равных по модулю, но противоположных по направлению сил 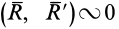 и может быть отброшена. Таким образом, рассматриваемая система сил оказалась эквивалентной одной равнодействующей силе
и может быть отброшена. Таким образом, рассматриваемая система сил оказалась эквивалентной одной равнодействующей силе 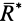 , которая по модулю и направлению совпадает с главным вектором
, которая по модулю и направлению совпадает с главным вектором 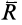 . Плечо пары сил
. Плечо пары сил 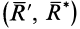 определяется из условия
определяется из условия
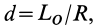
так как 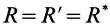 . Отрезок
. Отрезок 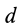 определяет кратчайшее расстояние от центра приведения
определяет кратчайшее расстояние от центра приведения 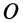 до линии действия равнодействующей силы
до линии действия равнодействующей силы 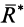 . Первый случай является частным случаем второго, когда за центр приведения
. Первый случай является частным случаем второго, когда за центр приведения 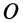 взята точка, расположенная на линии действия равнодействующей силы.
взята точка, расположенная на линии действия равнодействующей силы.
Приведение к динаме
Динамой в механике называют такую совокупность силы 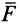 и пары сил
и пары сил  , действующих на твердое тело, у которой сила перпендикулярна плоскости действия пары сил (рис. 74). Используя векторный момент
, действующих на твердое тело, у которой сила перпендикулярна плоскости действия пары сил (рис. 74). Используя векторный момент 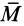 пары сил
пары сил 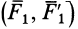 , можно также определить динаму как совокупность силы и пары, у которых сила параллельна векторному моменту пары сил (рис. 75). Сила
, можно также определить динаму как совокупность силы и пары, у которых сила параллельна векторному моменту пары сил (рис. 75). Сила 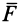 и векторный момент пары сил
и векторный момент пары сил 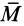 могут быть направлены как в одну, так и в противоположные стороны.
могут быть направлены как в одну, так и в противоположные стороны.
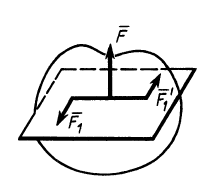
Рис. 74
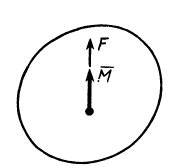
Рис. 75
Рассмотрим теперь случай, в котором 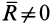 ,
, 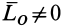 и векторы
и векторы 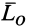 и
и 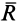 не перпендикулярны. В этом случае оба инварианта не равны нулю, т. е.
не перпендикулярны. В этом случае оба инварианта не равны нулю, т. е.
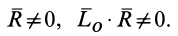
Покажем, что система сил в этом случае приводится к динаме, причем элементами динамы являются сила 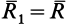 и момент-пары
и момент-пары 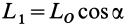 , где
, где 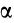 — угол между векторами
— угол между векторами 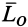 и
и 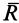 . Действительно, после приведения системы сил_ к центру О получим главный вектор
. Действительно, после приведения системы сил_ к центру О получим главный вектор 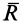 и главный момент
и главный момент 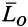 . Косинус угла а между ними можно определить выражая скалярное произведение векторов
. Косинус угла а между ними можно определить выражая скалярное произведение векторов 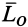 и
и 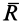 в двух формах:
в двух формах:
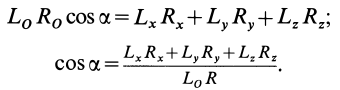
Разложим главный момент 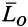 на две взаимно перпендикулярные составляющие
на две взаимно перпендикулярные составляющие 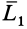 и
и 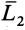 , одна из которых
, одна из которых 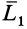 направлена по главному вектору
направлена по главному вектору 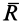 (рис. 76). Имеем
(рис. 76). Имеем
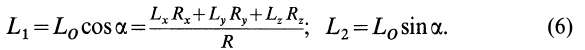
Векторный момент пары сил 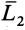 перпендикулярен главному вектору
перпендикулярен главному вектору 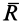 . Такая система силы
. Такая система силы 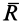 и пары с моментом
и пары с моментом 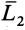 приведется к одной силе
приведется к одной силе 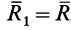 , линия действия которой находится от точки
, линия действия которой находится от точки 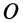 на расстоянии
на расстоянии
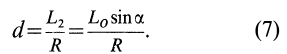
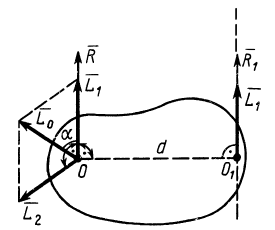
Рис. 76
Рассматриваемая система сил заменилась эквивалентной системой сил, состоящей из силы 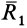 , и пары сил с векторным моментом
, и пары сил с векторным моментом 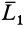 , который как свободный вектор можно перенести из точки
, который как свободный вектор можно перенести из точки 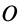 в любую точку, в том числе и точку
в любую точку, в том числе и точку 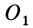 на линии действия силы
на линии действия силы 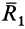 . Кратко результат можно выразить в форме
. Кратко результат можно выразить в форме
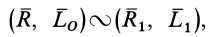
причем система сил 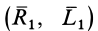 является динамой. Сила
является динамой. Сила 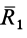 и векторный момент пары
и векторный момент пары 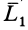 есть элементы динамы:
есть элементы динамы:
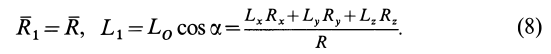
Линия, по которой направлена сила динамы, 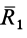 , называется центральной винтовой осью. Во всех точках винтовой оси, принятых за центры приведения, система сил приводится к одной и той же динаме. Расстояние от центра приведения
, называется центральной винтовой осью. Во всех точках винтовой оси, принятых за центры приведения, система сил приводится к одной и той же динаме. Расстояние от центра приведения 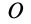 до центральной винтовой оси
до центральной винтовой оси
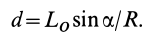
Если брать за центры приведения точки на поверхности цилиндра, осью которого является центральная винтовая ось, то главные моменты относительно таких центров будут одинаковы по модулю и составляют одинаковый угол с образующими цилиндра. Эти главные моменты состоят из одного и того же момента 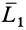 , входящего в состав динамы, и моментов
, входящего в состав динамы, и моментов 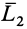 , перпендикулярных
, перпендикулярных 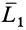 и по числовой величине пропорциональных расстоянию центра приведения от центральной винтовой оси.
и по числовой величине пропорциональных расстоянию центра приведения от центральной винтовой оси.
Совокупность сил, образующих динаму, можно заменить двумя скрещивающимися силами. Для этого следует одну из сил пары 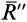 совместить с точкой приложения силы
совместить с точкой приложения силы 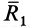 и сложить с этой силой (рис. 77).
и сложить с этой силой (рис. 77).
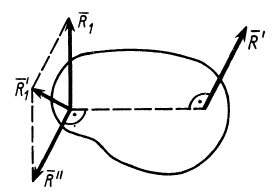
Рис. 77
Рассмотрены все возможные случаи, кроме_ случая равновесия системы сил 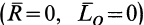 , рассмотренного ранее. Таким образом убедились, что только при обращении в нуль главного вектора и главного момента система может находиться в равновесии, т. е. обращение в нуль главного вектора и главного момента не только необходимо для равновесия системы сил, но и достаточно.
, рассмотренного ранее. Таким образом убедились, что только при обращении в нуль главного вектора и главного момента система может находиться в равновесии, т. е. обращение в нуль главного вектора и главного момента не только необходимо для равновесия системы сил, но и достаточно.
Из рассмотрения частных случаев приведения систем сил следует, что при приведении системы сил к равнодействующей силе 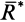 эта сила равна и параллельна главному вектору
эта сила равна и параллельна главному вектору 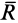 . Но линия действия равнодействующей может не проходить через центр приведения, в котором приложен главный вектор. Если главный вектор не равен нулю, то равнодействующей может и не быть, если система приводится к динаме.
. Но линия действия равнодействующей может не проходить через центр приведения, в котором приложен главный вектор. Если главный вектор не равен нулю, то равнодействующей может и не быть, если система приводится к динаме.
Уравнение центральной винтовой оси
Предположим, что в центре приведения, принятом за начало координат, получены главный вектор 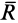 с проекциями на оси координат
с проекциями на оси координат 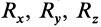 и главный момент
и главный момент 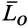 с проекциями
с проекциями 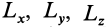 . При приведении системы сил к центру приведения
. При приведении системы сил к центру приведения 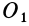 (рис.78) получается динама с главным вектором
(рис.78) получается динама с главным вектором 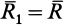 и главным моментом
и главным моментом 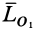 . Векторы
. Векторы 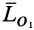 и
и 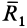 как образующие динаму, параллельны и поэтому могут отличаться только скалярным множителем
как образующие динаму, параллельны и поэтому могут отличаться только скалярным множителем 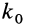 . Имеем
. Имеем

так как 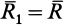 . Главные моменты
. Главные моменты 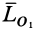 и
и 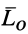 удовлетворяют соотношению
удовлетворяют соотношению

Подставляя 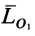 из (2') в (9), получим
из (2') в (9), получим

Координаты точки 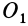 в которой получена динама, обозначим
в которой получена динама, обозначим 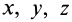 . Тогда проекции вектора
. Тогда проекции вектора 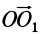 на оси координат равны координатам
на оси координат равны координатам 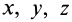 . Учитывая это, (9') можно выразить в форме
. Учитывая это, (9') можно выразить в форме
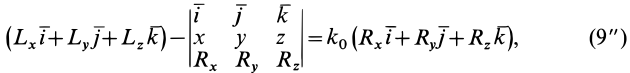
где 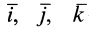 —единичные векторы осей координат, а векторное произведение
—единичные векторы осей координат, а векторное произведение 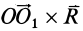 представлено определителем. Векторное уравнение (9") эквивалентно трем скалярным, которые после отбрасывания
представлено определителем. Векторное уравнение (9") эквивалентно трем скалярным, которые после отбрасывания 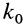 можно представить в виде
можно представить в виде
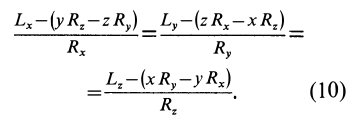
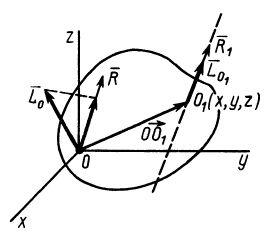
Рис. 78
Линейные уравнения (10) для координат 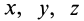 являются уравнениями прямой линии — центральной винтовой оси. Следовательно, существует прямая, в точках которой система сил приводится к динаме.
являются уравнениями прямой линии — центральной винтовой оси. Следовательно, существует прямая, в точках которой система сил приводится к динаме.
Пример 1.
По ребрам куба с длиной стороны 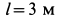 действуют силы
действуют силы 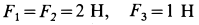 (рис. 79). Привести систему сил
(рис. 79). Привести систему сил 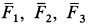 к простейшему виду.
к простейшему виду.
Решение. Выберем точку 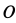 — начало координат— за центр приведения сил и вычислим главный вектор
— начало координат— за центр приведения сил и вычислим главный вектор 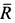 и главный момент
и главный момент 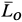 . Для проекций этих векторов на оси координат имеем:
. Для проекций этих векторов на оси координат имеем:
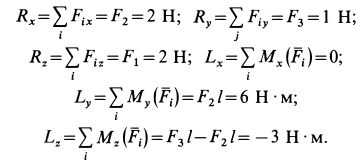
Величины главного вектора и главного момента имеют значения
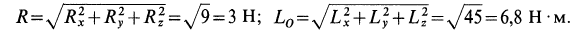
Определим угол 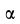 между векторами
между векторами 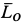 и
и 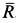 . Для этого образуем их скалярное произведение, которое выразим в двух следующих формах:
. Для этого образуем их скалярное произведение, которое выразим в двух следующих формах:
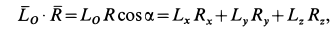
или
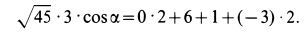
Отсюда получаем 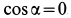 , т. е. векторы
, т. е. векторы 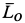 и
и 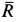 перпендикулярны. Система сил в этом случае приводится к равнодействующей, которая по величине и направлению равна главному вектору, т.е.
перпендикулярны. Система сил в этом случае приводится к равнодействующей, которая по величине и направлению равна главному вектору, т.е. 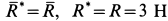 .
.
Кратчайшее расстояние от точки 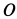 (рис. 80) до линии действия равнодействующей вычислим по формуле
(рис. 80) до линии действия равнодействующей вычислим по формуле
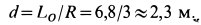
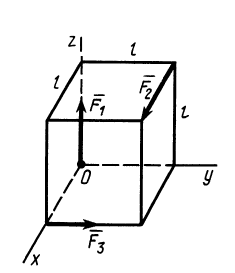
Рис. 79
Пример 2.
К балке 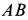 , один конец которой заделан в сечении
, один конец которой заделан в сечении 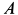 , в точке
, в точке 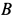 приложена вертикальная сила
приложена вертикальная сила 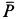 (рис. 81, а). К балке
(рис. 81, а). К балке 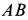 в сечении
в сечении 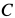 под прямым углом жестко прикреплена балка
под прямым углом жестко прикреплена балка 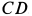 . В концевом сечении балки
. В концевом сечении балки 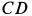 в плоскости, параллельной координатной плоскости
в плоскости, параллельной координатной плоскости 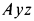 , действует пара сил с моментом
, действует пара сил с моментом 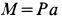 . Размеры тел и направление вращения пары сил указаны на рисунке. Определить силу и момент пары сил в заделке.
. Размеры тел и направление вращения пары сил указаны на рисунке. Определить силу и момент пары сил в заделке.
Решение. Рассматриваемые вместе балки 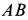 и
и 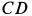 освобождаем от связей. Заделка для пространственной системы сил создает неизвестную силу
освобождаем от связей. Заделка для пространственной системы сил создает неизвестную силу 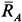 с проекциями на оси координат
с проекциями на оси координат 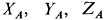 и пару сил с векторным моментом
и пару сил с векторным моментом 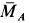 , проекции которого на координатные оси —
, проекции которого на координатные оси — 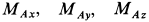 (рис. 81,6).
(рис. 81,6).
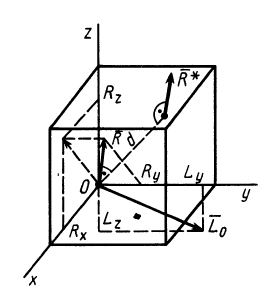
Рис. 80
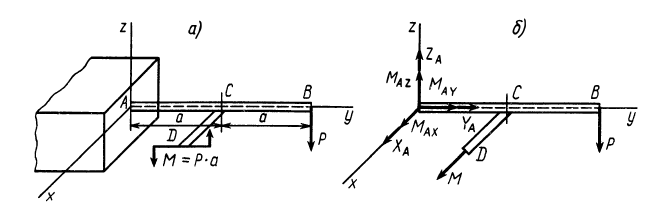
Рис. 81
В общем случае имеем шесть неизвестных. Для их определения составляем шесть условий равновесия пространственной системы сил. При проецировании сил на оси координат пары сил учитывать не надо, так как сумма проекций пары сил на любую ось равна нулю. В уравнения равновесия для моментов сил относительно осей координат следует включать проекции векторных моментов пар сил на эти оси. Для удобства проецирования пару сил в концевом сечении балки 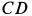 представим ее векторным моментом
представим ее векторным моментом 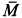 , который в рассматриваемом случае направлен по балке
, который в рассматриваемом случае направлен по балке 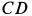 параллельно оси
параллельно оси 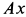 .
.
Составляем условия равновесия:
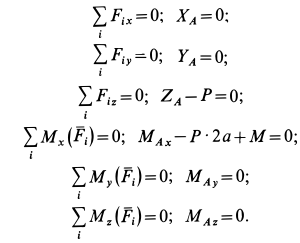
Учитывая, что 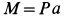 , имеем:
, имеем:
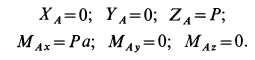
Задача считается решенной, если определены проекции неизвестных силы 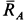 и момента пары сил
и момента пары сил 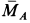 на какие-либо прямоугольные оси координат.
на какие-либо прямоугольные оси координат.
Пример 3.
Изогнутый под прямым углом стержень 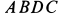 находится в горизонтальной плоскости. Стержень закреплен с помощью подпятника
находится в горизонтальной плоскости. Стержень закреплен с помощью подпятника 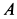 и подшипника
и подшипника 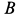 (рис. 82). На стержень под прямым углом жестко насажен диск радиуса
(рис. 82). На стержень под прямым углом жестко насажен диск радиуса 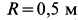 . В плоскости диска по касательной действует сила
. В плоскости диска по касательной действует сила 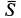 под углом
под углом 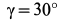 к вертикали. В точке
к вертикали. В точке 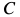 стержня приложена сила
стержня приложена сила 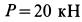 под углом
под углом 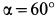 к вертикали и углом
к вертикали и углом 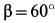 к линии
к линии 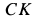 , которая находится в плоскости
, которая находится в плоскости 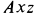 .
.
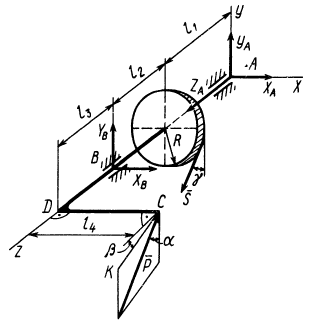
Рис. 82
Определить силы реакций подпятника и подшипника, а также значение силы 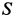 , необходимой для равновесия, если
, необходимой для равновесия, если 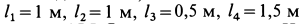 .
.
Решение. Рассмотрим равновесие стержня 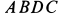 вместе с диском. На эту систему тел действуют силы
вместе с диском. На эту систему тел действуют силы 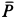 ,
, 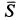 ; реакция в подпятнике с составляющими
; реакция в подпятнике с составляющими 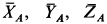 , реакция в подшипнике с составляющими
, реакция в подшипнике с составляющими 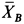 и
и 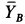 , которые предполагаем направленными в положительные стороны осей координат.
, которые предполагаем направленными в положительные стороны осей координат.
Составим шесть условий равновесия для сил. Для проекций сил на оси координат имеем:
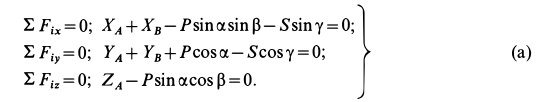
При определении проекций силы 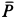 на оси координат предварительно раскладываем ее на две перпендикулярные составляющие, одна из которых параллельна оси
на оси координат предварительно раскладываем ее на две перпендикулярные составляющие, одна из которых параллельна оси 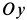 и имеет проекцию на эту ось
и имеет проекцию на эту ось 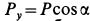 . Перпендикулярная составляющая расположится в плоскости
. Перпендикулярная составляющая расположится в плоскости 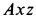 и будет иметь величину проекции на эту плоскость
и будет иметь величину проекции на эту плоскость
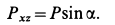
Силу 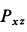 как вектор проецируем на оси координат
как вектор проецируем на оси координат 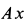 и
и 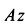 . Имеем
. Имеем
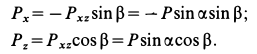
Для моментов сил относительно осей координат получаем:
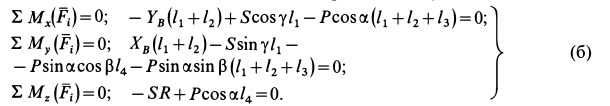
При вычислении момента силы относительно оси координат, согласно определению, проецируем силу на плоскость, перпендикулярную оси, и затем вычисляем момент проекции силы относительно точки пересечения оси с плоскостью. Силы, параллельные оси или ее пересекающие, дают моменты относительно этой оси, равные нулю. При определении момента силы 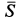 относительно осей координат раскладываем ее на составляющие, параллельные осям координат, вычисляем на основании теоремы Вариньона моменты каждой из составляющих относительно соответствующих осей координат и складываем их алгебраически. Значения составляющих сил равны проекциям этих сил на оси координат и их можно взять из уравнений (а). Аналогично вычисляются моменты силы
относительно осей координат раскладываем ее на составляющие, параллельные осям координат, вычисляем на основании теоремы Вариньона моменты каждой из составляющих относительно соответствующих осей координат и складываем их алгебраически. Значения составляющих сил равны проекциям этих сил на оси координат и их можно взять из уравнений (а). Аналогично вычисляются моменты силы 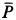 .
.
Решая систему линейных уравнений (а) и (б) относительно проекций неизвестных сил, можно определить все неизвестные силы.
Подставляя в уравнения (а) и (б) заданные значения сил, расстояний и углов, получим:
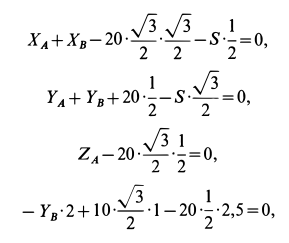
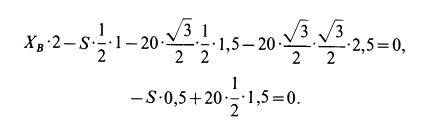
Решая эту систему уравнений, имеем:
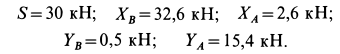
Частные случаи приведения пространственной системы параллельных сил
В отличие от произвольной системы сил пространственная система параллельных сил не приводится к динаме, так как для нее главный вектор и главный момент в общем случае взаимно перпендикулярны. Для доказательства этого рассмотрим пространственную систему параллельных сил, для которой главный вектор и главный момент не равны нулю. Выберем за центр приведения точку 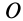 — начало декартовой системы координат, ось
— начало декартовой системы координат, ось 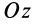 которой направим параллельно силам (рис. 83). Тогда проекции главного вектора на оси координат
которой направим параллельно силам (рис. 83). Тогда проекции главного вектора на оси координат
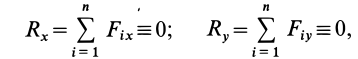
так как параллельные силы перпендикулярны этим осям. Только проекция главного вектора на ось 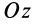 в общем случае не равна нулю. Она равна алгебраической сумме параллельных сил, т. е.
в общем случае не равна нулю. Она равна алгебраической сумме параллельных сил, т. е.
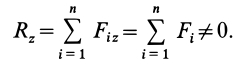
Следовательно, главный вектор 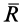 параллелен оси
параллелен оси 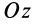 .
.
Для проекций главного момента на оси координат имеем:
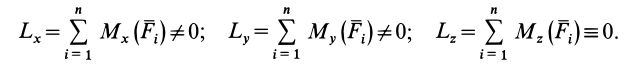
Проекция главного момента на ось 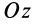 равна нулю, так как каждая сила параллельна этой оси.
равна нулю, так как каждая сила параллельна этой оси.
Таким образом, главный момент расположен в плоскости 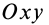 , перпендикулярной главному вектору, направленному по оси
, перпендикулярной главному вектору, направленному по оси 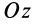 . В этом случае система сил приводится к равнодействующей.
. В этом случае система сил приводится к равнодействующей.
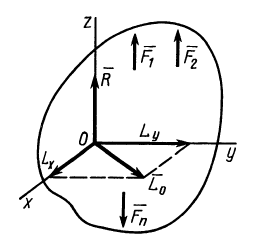
Рис. 83
Для системы параллельных сил возможны следующие частные случаи приведения:
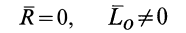
— система приводится к паре сил;
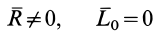
или
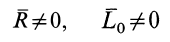
— система приводится к равнодействующей силе;

— имеем равновесную систему сил.
Если главный вектор не равен нулю, то система параллельных сил приводится только к равнодействующей силе, параллельной главному вектору и равной ему по величине.
Центр системы параллельных сил
Для систем параллельных сил, приводящихся к равнодействующей, введем понятие центра параллельных сил. Для этого предположим,_ что на твердое тело действует система параллельных сил 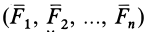 , приводящаяся к равнодействующей, силы которой приложены в точках
, приводящаяся к равнодействующей, силы которой приложены в точках 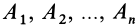 . При введении понятия центра параллельных сил считаем силы приложенными в точках твердого тела. При переносе сил вдоль линий действия положение центра параллельных сил изменяется.
. При введении понятия центра параллельных сил считаем силы приложенными в точках твердого тела. При переносе сил вдоль линий действия положение центра параллельных сил изменяется.
Определим линию действия равнодействующей 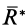 параллельных сил для заданного направления этих сил. Затем через точки приложения параллельных сил проведем взаимно параллельные оси, перпендикулярные силам. Повернем параллельные силы вокруг этих осей на общий угол в одном и том же направлении (рис. 84). Получим новую систему параллельных сил
параллельных сил для заданного направления этих сил. Затем через точки приложения параллельных сил проведем взаимно параллельные оси, перпендикулярные силам. Повернем параллельные силы вокруг этих осей на общий угол в одном и том же направлении (рис. 84). Получим новую систему параллельных сил 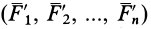 . Равнодействующая этой системы параллельных сил
. Равнодействующая этой системы параллельных сил 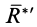 равна по модулю равнодействующей силе
равна по модулю равнодействующей силе 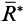 , так как при повороте числовые значения параллельных сил не изменялись.
, так как при повороте числовые значения параллельных сил не изменялись.
Линии действия двух равнодействующих сил 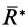 и
и 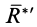 пересекутся в точке
пересекутся в точке 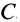 , которая и называется центром параллельных сил. Если равнодействующую силу
, которая и называется центром параллельных сил. Если равнодействующую силу 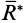 приложить в точке
приложить в точке 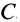 вместо
вместо 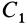 то при повороте заданных параллельных сил
то при повороте заданных параллельных сил 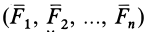 на угол
на угол 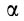 она повернется на тот же угол
она повернется на тот же угол 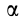 вокруг оси, проходящей через точку
вокруг оси, проходящей через точку 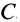 и параллельной осям, вокруг которых поворачиваются заданные параллельные силы. Оси поворота параллельных сил должны быть перпендикулярны параллельным силам.
и параллельной осям, вокруг которых поворачиваются заданные параллельные силы. Оси поворота параллельных сил должны быть перпендикулярны параллельным силам.
Центр параллельных сил не зависит от угла поворота и направления параллельных осей, вокруг которых поворачиваются параллельные силы. Из определения центра параллельных сил следует, что его положение зависит от точек приложения параллельных сил. Поэтому параллельные силы следует считать приложенными в точках твердого тела.
Получим формулу для определения радиуса-вектора центра параллельных сил, если известны параллельные силы и радиусы-векторы точек их приложения. Для этого выберем единичный вектор 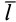 , параллельный силам. Тогда каждая из параллельных сил
, параллельный силам. Тогда каждая из параллельных сил
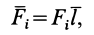
где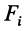 — алгебраическое значение силы. Оно положительно, если сила
— алгебраическое значение силы. Оно положительно, если сила 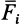 направлена в одну сторону с единичным вектором
направлена в одну сторону с единичным вектором 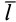 , и отрицательно, если направление силы противоположно направлению единичного вектора.
, и отрицательно, если направление силы противоположно направлению единичного вектора.
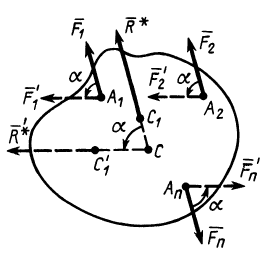
Рис. 84
Для равнодействующей силы параллельных сил соответственно имеем
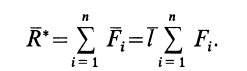
Так как система параллельных сил, по предположению, приводится к равнодействующей, то к ней можно применить теорему Вариньона относительно точки 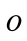 :
:
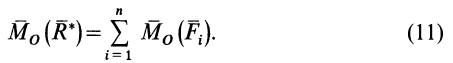
Для векторных моментов сил относительно точки 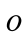 имеем
имеем
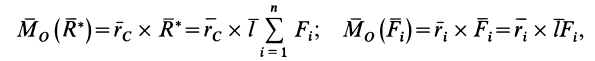
где 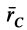 — радиус-вектор центра параллельных сил, проведенный из точки
— радиус-вектор центра параллельных сил, проведенный из точки 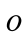 ;
; 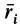 — радиус-вектор точки приложения силы
— радиус-вектор точки приложения силы 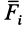 , проведенный из той же точки (рис. 85).
, проведенный из той же точки (рис. 85).
Если подставить эти значения векторных моментов сил в (11), то после переноса всех слагаемых в левую часть равенства и вынесения за скобку общего множителя 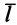 получим
получим
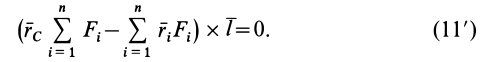
Так как центр параллельных сил, а следовательно, и его радиус-вектор не зависят от направления параллельных сил, характеризуемого единичным вектором 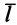 , то условие (11') должно выполняться при любом направлении этого вектора.
, то условие (11') должно выполняться при любом направлении этого вектора.
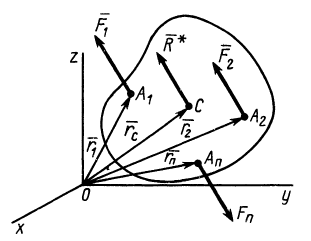
Рис. 85
Это возможно только при обращении в нуль векторной величины, стоящей в скобках, т. е.
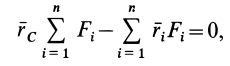
или
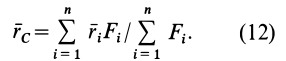
По формуле (12) определяют радиус-вектор центра параллельных сил, если заданы эти силы и их точки приложения.
Так как алгебраические значения параллельных сил входят в числитель и в знаменатель (12), то 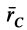 не зависит от того, какое из двух направлений параллельных сил считается положительным.
не зависит от того, какое из двух направлений параллельных сил считается положительным.
В проекциях на оси координат из (12) получаем:
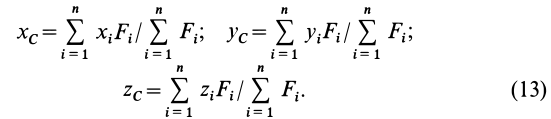
По формулам (13) вычисляют координаты центра параллельных сил 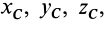 если известны алгебраические значения параллельных сил
если известны алгебраические значения параллельных сил 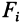 и координаты точек приложения этих сил
и координаты точек приложения этих сил 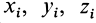 .
.
Векторную величину
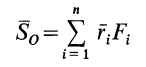
называют статическим моментом системы параллельных сил относительно точки 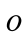 . Алгебраические величины
. Алгебраические величины
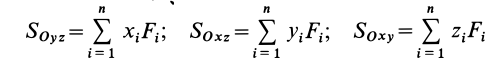
называют статическими моментами относительно координатных плоскостей. Для плоской системы параллельных сил, расположенных, например, в плоскости 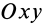 , вводят понятие статических моментов относительно осей координат
, вводят понятие статических моментов относительно осей координат 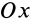 и
и 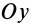 по формулам
по формулам
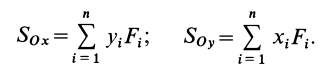
Статические моменты параллельных сил относительно точки и координатных плоскостей определяются по единому правилу: алгебраические значения сил умножают на расстояния от точек приложения сил до точки или плоскости и результаты суммируют. Расстояния от точек приложения сил до координатных плоскостей есть величины скалярные; это соответствующие координаты этих точек. Расстояния от точки 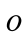 до точек приложения параллельных сил берутся векторные. Ими являются радиусы-векторы точек приложения параллельных сил, проведенные из точки
до точек приложения параллельных сил берутся векторные. Ими являются радиусы-векторы точек приложения параллельных сил, проведенные из точки 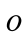 .
.
Частные случаи равновесия твердого тела
Равновесие твердого тела с двумя закрепленными точками
Твердое тело с двумя закрепленными точками 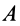 и
и 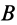 имеет неподвижную ось вращения, проходящую через эти точки. Пусть тело находится в равновесии под действием приложенных сил
имеет неподвижную ось вращения, проходящую через эти точки. Пусть тело находится в равновесии под действием приложенных сил 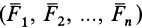 . Освободим тело от связей, приложив в закрепленных точках
. Освободим тело от связей, приложив в закрепленных точках 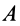 и
и 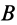 , рассматриваемых как шаровые шарниры без трения, не известные по модулю и направлению силы реакций
, рассматриваемых как шаровые шарниры без трения, не известные по модулю и направлению силы реакций 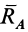 и
и 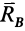 . Эти силы разложим на составляющие, параллельные осям координат
. Эти силы разложим на составляющие, параллельные осям координат 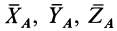 и
и 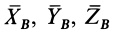 , и для освобожденного от связей тела составим шесть условий равновесия сил. Обозначив
, и для освобожденного от связей тела составим шесть условий равновесия сил. Обозначив 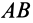 через
через 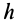 (рис. 86), получим:
(рис. 86), получим:
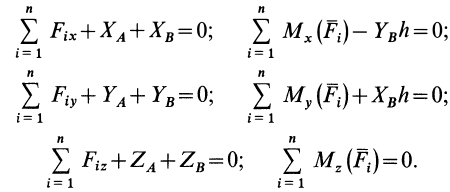
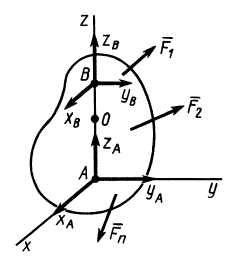
Рис. 86
Пять первых уравнений содержат неизвестные реакции закрепленных точек, поэтому их называют уравнениями равновесия. В последнее (шестое) уравнение входят только заданные силы и не входят неизвестные силы реакций. Такие соотношения, которым должны удовлетворять при равновесии тела только одни заданные силы, называют условиями равновесия. Тело в рассматриваемом случае имеет одну степень свободы, оно может только вращаться вокруг оси 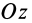 (ось
(ось 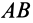 ). Приложенные силы удовлетворяют тоже одному условию равновесия. Сумма моментов заданных сил относительно оси
). Приложенные силы удовлетворяют тоже одному условию равновесия. Сумма моментов заданных сил относительно оси 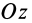 обращается в ноль. В остальном приложенные силы могут быть любыми. Изменяя систему приложенных сил так, чтобы они удовлетворяли при этом условию равновесия, получим в соответствии с уравнениями равновесия каждый раз свои силы реакций.
обращается в ноль. В остальном приложенные силы могут быть любыми. Изменяя систему приложенных сил так, чтобы они удовлетворяли при этом условию равновесия, получим в соответствии с уравнениями равновесия каждый раз свои силы реакций.
Неизвестных реакций шесть, а уравнений для их определения только пять и, следовательно, только пять неизвестных можно определить. Из рассмотрения уравнений равновесия убеждаемся, что нельзя по отдельности определить 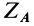 и
и 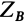 , можно определить только их сумму
, можно определить только их сумму 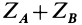 . Задача нахождения сил реакций является статически неопределимой. Для того чтобы ее сделать статически определимой, в одной из точек вместо шарового следует установить цилиндрический шарнир. Если цилиндрический шарнир поместить в точке
. Задача нахождения сил реакций является статически неопределимой. Для того чтобы ее сделать статически определимой, в одной из точек вместо шарового следует установить цилиндрический шарнир. Если цилиндрический шарнир поместить в точке 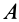 , то
, то 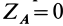 , так как реакция цилиндрического шарнира перпендикулярна его оси; в рассматриваемом случае перпендикулярна оси
, так как реакция цилиндрического шарнира перпендикулярна его оси; в рассматриваемом случае перпендикулярна оси 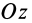 . После этого неизвестных реакций останется только пять. Столько же уравнений имеется для их определения.
. После этого неизвестных реакций останется только пять. Столько же уравнений имеется для их определения.
Твердое тело с одной закрепленной точкой
Тело с одной закрепленной точкой имеет три степени свободы. Оно, например, может вращаться вокруг каждой из трех осей координат, проходящих через закрепленную точку. Если твердое тело с одной закрепленной точкой 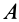 , принимаемой за шарнир, освободить от этой связи, то для составляющих силы реакций связи
, принимаемой за шарнир, освободить от этой связи, то для составляющих силы реакций связи 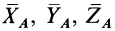 и приложенных к телу сил
и приложенных к телу сил 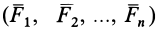 можно составить следующие шесть условий (рис. 87):
можно составить следующие шесть условий (рис. 87):
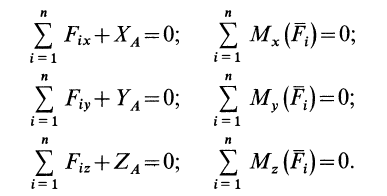
В этом случае имеем три уравнения равновесия с тремя неизвестными. Задача статически определима. Приложенные силы удовлетворяют тоже трем условиям равновесия, т. е. равны нулю суммы моментов приложенных сил относительно каждой из трех осей координат. В эти условия не входят неизвестные силы реакций. Существует много разных систем сил, удовлетворяющих этим трем условиям. Для каждой из таких систем приложенных сил получим свои реакции связи.
В рассмотренных двух случаях число условий равновесия, которым должны удовлетворять заданные силы при равновесии твердого тела, совпало с числом степеней свободы этого тела. Это справедливо и для свободного твердого тела, у которого шесть степеней свободы и соответственно шесть условий равновесия для сил. При изучении аналитической статики, которая излагается вместе с аналитической динамикой (в одной главе), увидим, что число степеней свободы не только для твердого тела, но и для механических систем совпадает с числом условий равновесия для заданных сил, если связи, наложенные на систему, удовлетворяют некоторым специальным условиям.
Рис. 87
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |