
Пространственная система сходящихся сил в теоретической механике
Пространственная система сходящихся сил:
До сих пор мы рассматривали силы, которые были расположены в одной плоскости. Пусть к точке О (рис. 91) приложены три силы 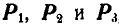
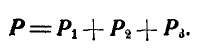
Из рисунка 92 видно, что равнодействующая трех сил 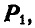
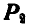 и
и 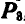 , не лежащих в одной плоскости, равна по величине и направлению диагонали параллелепипеда, построенного на этих силах. Такое правило сложения трех сил называется правилом параллелепипеда.
, не лежащих в одной плоскости, равна по величине и направлению диагонали параллелепипеда, построенного на этих силах. Такое правило сложения трех сил называется правилом параллелепипеда.
Нетрудно видеть (рис. 91), что равнодействующая Р трех сил 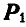 , и
, и  , не лежащих в одной плоскости, является также замыкающей пространственного многоугольника, построенного на этих силах.
, не лежащих в одной плоскости, является также замыкающей пространственного многоугольника, построенного на этих силах.
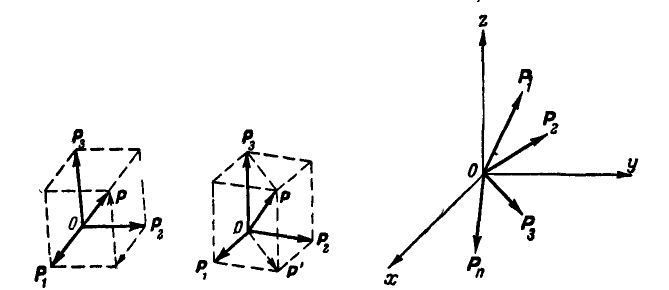
Рис. 92. Рис. 91. Рис. 93.
Вообще же, если на точку О действуют 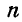 сил (рис. 93), расположенных не в одной плоскости, то, складывая эти силы геометрически по правилу сложения векторов, получим пространственный многоугольник, замыкающая которого и будет равнодействующей данных сил.
сил (рис. 93), расположенных не в одной плоскости, то, складывая эти силы геометрически по правилу сложения векторов, получим пространственный многоугольник, замыкающая которого и будет равнодействующей данных сил.
Обозначая равнодействующую через Р, имеем:
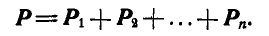
Проектируя равнодействующую и составляющие на координатные оси х, у и z, получим:
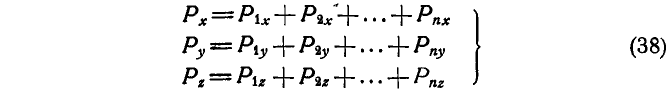
Величина и направление равнодействующей определяется по формулам (6) и (7):
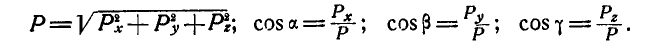
Если многоугольник сил окажется замкнутым, то 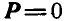 и силы, приложенные к точке, взаимно уравновешиваются; в этом случае
и силы, приложенные к точке, взаимно уравновешиваются; в этом случае 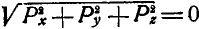 , а для этого необходимо, чтобы:
, а для этого необходимо, чтобы:
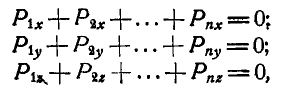
или более сокращенно:
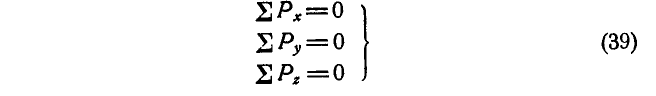
Уравнения (39) называются уравнениями равновесия сил, приложенных к точке.
Задача:
Определить величину и направление равнодействующей пяти сил 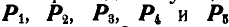 , приложенных к точке О, если концы сил совпадают с вершинами куба и
, приложенных к точке О, если концы сил совпадают с вершинами куба и 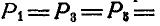 2 т (рис. 94).
2 т (рис. 94).
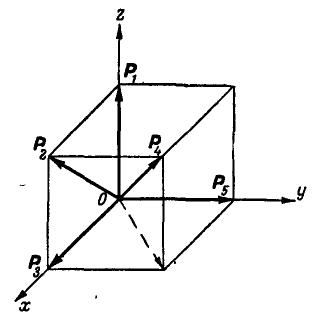
Рис. 94.
Решение:
Величины сил 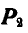 и
и 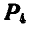 найдутся соответственно как диагонали квадрата и куба:
найдутся соответственно как диагонали квадрата и куба:
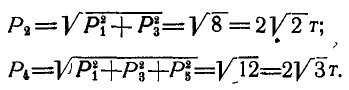
Проекции равнодействующей на координатные оси х, у и z:
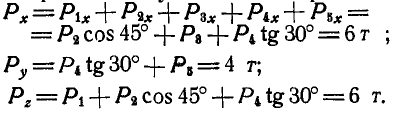
Для нахождения проекции 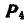 на ось х проектируем сначала силу
на ось х проектируем сначала силу 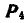 на плосхость хОу и полученную проекцию вновь проектируем уже на ось х. Обозначив через
на плосхость хОу и полученную проекцию вновь проектируем уже на ось х. Обозначив через 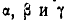 углы, которые составляет сила
углы, которые составляет сила 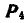 с осями
с осями 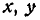 и
и 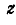 , найдем:
, найдем: 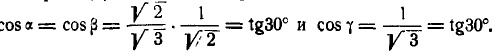
Величина равнодействующей 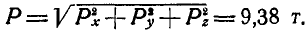 Направление равнодействующей определится косинусами углов, которые она составляет с осями:
Направление равнодействующей определится косинусами углов, которые она составляет с осями:
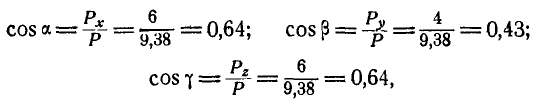
Решение. Освобождаемся от связей и рассматриваем равновесие точки В (рис. 95, б):
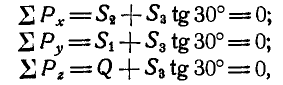
откуда находим: 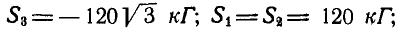
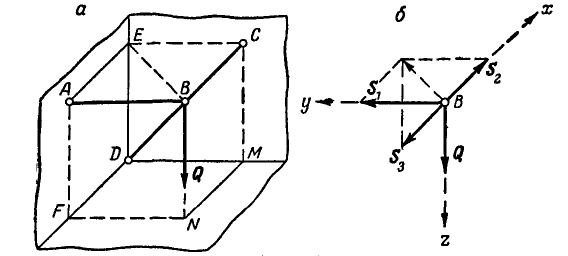
Рис. 95.
Задача:
Для транспортировки груза Q = 6 т устроена подвесная дорога, состоящая из троса АВС и столбов AD и СЕ, удерживаемых стальными тягами AN, AM, CF и СО, так, что вертикальная плоскость ALDEKC делит двугранные углы AMDN и CFEO пополам (рис. 98, а).
Определить усилие S в столбах и натяжения 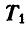 и
и 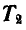 в тягах, удерживающих столбы, если АВ = ВС = 5 м.
в тягах, удерживающих столбы, если АВ = ВС = 5 м.
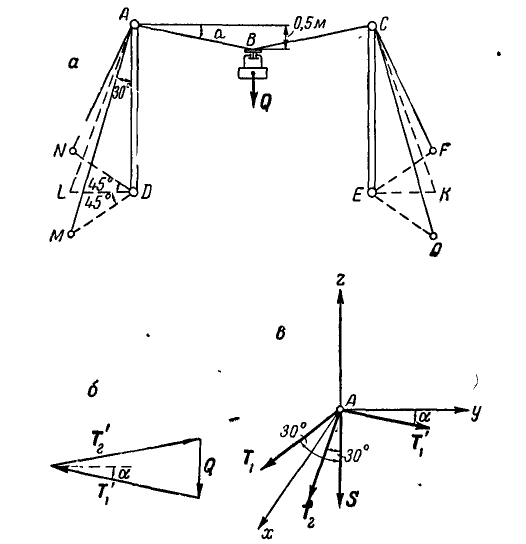
Рис. 98.
Решение:
Определим сначала натяжения 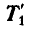 и
и 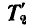 , в частях троса АВ и ВС, для чего построим треугольник равновесия для точки В (рис. 98, б).
, в частях троса АВ и ВС, для чего построим треугольник равновесия для точки В (рис. 98, б).
Из чертежа видно, что 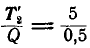 , откуда
, откуда
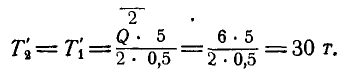
Составляя уравнения равновесия (39) для точки А (рис. 98, в), имеем:
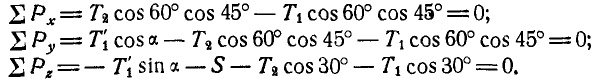
Решая полученные уравнения, находим: 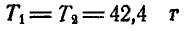 и
и 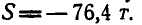
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Момент силы относительно точки и относительно оси
- Теория пар, не лежащих в одной плоскости
- Произвольная пространственная система сил
- Центр параллельных сил и центр тяжести
- Произвольная плоская система сил
- Равновесие системы, состоящей из нескольких тел
- Графостатика в теоретической механике
- Расчет ферм