
Простейший (пуассоновский) поток событий - определение и вычисление с примером решения
Простейший (пуассоновский) поток событий:
Потоком событий называется последовательность событий, происходящих одно за другим в случайные моменты времени. Например, телефонные вызовы, автомобили, подъезжающие к перекрестку, выходы из строя некоторого устройства, покупатели, приходящие в магазин и т.д. Для наглядности можно изображать моменты наступления событий точками на оси времени. События могут распределяться не только во времени, но и в пространстве (например, опечатки в тексте, капли дождя на асфальте, пожары в городе и т.д.).

На рис. 2.7.1 точками отмечены моменты поступления событий, 
Одним из самых интересных и в математическом плане и с точки зрения приложений является пуассоновский или простейший поток.
Поток событий называется простейшим или пуассоновским, если выполняются следующие условия:
1. Появление того или иного числа событий на интервале времени длины 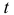 зависит только от длины этого интервала и не зависит от его расположения на оси времени и от требований, приходящих вне этого интервала.
зависит только от длины этого интервала и не зависит от его расположения на оси времени и от требований, приходящих вне этого интервала.
Обозначим через 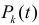 вероятность появления
вероятность появления 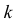 событий на интервале времени длины
событий на интервале времени длины 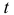 .
.
2. Вероятность появления одного события за малый промежуток времени 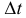 пропорциональна длине этого промежутка, т.е.
пропорциональна длине этого промежутка, т.е. 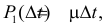 где
где 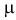 – некоторая постоянная.
– некоторая постоянная.
3. Вероятность появления двух или более событий за малый промежуток времени 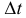 есть величина более высокого порядка малости по сравнению с
есть величина более высокого порядка малости по сравнению с 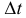 .
.
Независимость вероятностей 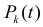 от расположения отрезка длины
от расположения отрезка длины 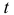 на числовой оси означает стационарность потока, а независимость от событий вне отрезка означает отсутствие последействия, т.е. независимость событий потока.
на числовой оси означает стационарность потока, а независимость от событий вне отрезка означает отсутствие последействия, т.е. независимость событий потока.
Из условий 2 и 3 следует, что за малый промежуток времени 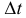 может либо наступить одно событие, либо ни одного события не поступит. Остальными возможностями можно пренебречь. В этом случае говорят, что поток событий ординарен, т.е. события происходят по одному, а не группами. Формально свойства 2 и 3 означают, что
может либо наступить одно событие, либо ни одного события не поступит. Остальными возможностями можно пренебречь. В этом случае говорят, что поток событий ординарен, т.е. события происходят по одному, а не группами. Формально свойства 2 и 3 означают, что 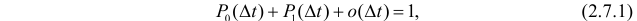
или
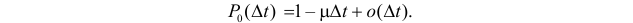
Построим математическую модель простейшего потока. Прежде всего из определения простейшего потока выведем формулы для вероятностей 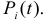
Чтобы не заниматься выводом формулы для каждой вероятности отдельно, рассмотрим так называемую производящую функцию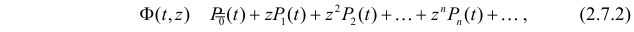
для которой интересующие нас вероятности служат коэффициентами ее разложения в ряд по степеням z.
Выберем 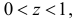 и будем считать, что каждое событие потока независимо от других может оказаться «красным» с вероятностью z. Такая условная раскраска событий позволяет придать функции
и будем считать, что каждое событие потока независимо от других может оказаться «красным» с вероятностью z. Такая условная раскраска событий позволяет придать функции 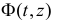 вероятностный смысл, что упрощает дальнейшие рассуждения по выводу для нее дифференциального уравнения.
вероятностный смысл, что упрощает дальнейшие рассуждения по выводу для нее дифференциального уравнения.
Выражение 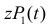 можно понимать как вероятность того, что за время
можно понимать как вероятность того, что за время 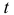 поступило одно событие и оно оказалось «красным»,
поступило одно событие и оно оказалось «красным», 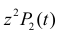 – можно считать вероятностью того, что за время
– можно считать вероятностью того, что за время 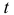 поступило два события и они оба «красные». В свою очередь,
поступило два события и они оба «красные». В свою очередь, 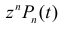 можно расценивать как вероятность того, что за время
можно расценивать как вероятность того, что за время 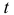 поступило
поступило 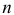 «красных» событий. Это дает возможность понимать
«красных» событий. Это дает возможность понимать 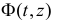 как полную вероятность того, что за время
как полную вероятность того, что за время 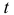 поступили только «красные» события.
поступили только «красные» события.
Составим уравнение для определения 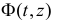 . Рассмотрим отрезок
. Рассмотрим отрезок 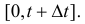 За время
За время 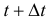 наступят только красные события, вероятность чего равна
наступят только красные события, вероятность чего равна 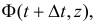 если за время
если за время 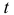 наступят только «красные» события, вероятность чего равна
наступят только «красные» события, вероятность чего равна 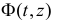 , и за время
, и за время 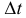 либо не произойдет событий, вероятность чего равна
либо не произойдет событий, вероятность чего равна 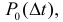 D либо произойдет одно событие и оно будет красным, вероятность чего равна
D либо произойдет одно событие и оно будет красным, вероятность чего равна 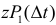 . Эту фразу можно символически записать в виде
. Эту фразу можно символически записать в виде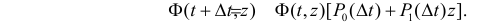
Возможностью прихода двух или более требований за малое время 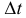 пренебрегаем в силу ординарности потока. Последнее равенство с учетом (2.7.1) можно переписать в форме
пренебрегаем в силу ординарности потока. Последнее равенство с учетом (2.7.1) можно переписать в форме
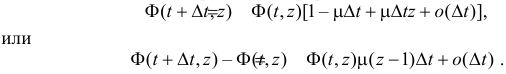
После деления обеих частей равенства на 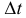 и перехода к пределу при
и перехода к пределу при 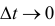 получаем уравнение
получаем уравнение

причем 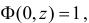 так как
так как 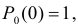 а все
а все 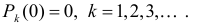
Решением этого дифференциального уравнения при указанном начальном условии является функция

Разложение этой функции в ряд по степеням z имеет вид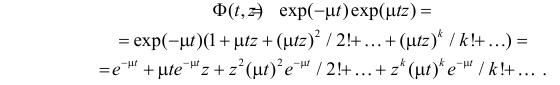
Сравнение с записью (2.7.2) приводит к выводу, что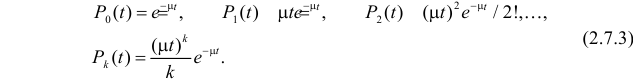
Величина 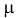 называется интенсивностью простейшего потока. Она равна среднему числу событий, происходящих в единицу времени. Среднее число событий, происходящих за время
называется интенсивностью простейшего потока. Она равна среднему числу событий, происходящих в единицу времени. Среднее число событий, происходящих за время 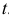 , равно
, равно 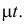 Полученный результат можно не строго сформулировать следующим образом. Если события приходят независимо друг от друга и по одному и известно, что на данный интервал времени в среднем приходится
Полученный результат можно не строго сформулировать следующим образом. Если события приходят независимо друг от друга и по одному и известно, что на данный интервал времени в среднем приходится 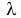 событий, то вероятность появления на этом интервале равно
событий, то вероятность появления на этом интервале равно 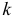 событий равна
событий равна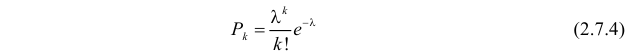
Стоит обратить внимание на то, что этот сильный количественный результат получен из очень простых предположений. Можно назвать много примеров, где эти предположения приблизительно выполняются (телефонные звонки, опечатки в тексте, радиоактивный распад и т.д.). Причина такого широкого распространения пуассоновских потоков состоит в том, что пуассоновский поток является предельным потоком. В том смысле, что сумма большого числа независимых потоков малой интенсивности близка по своим свойствам к пуассоновскому потоку (см. рис. 2.7.2).
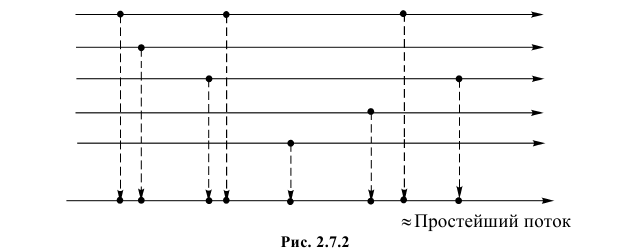
Именно такими суммарными потоками являются потоки вызовов на телефонную станцию, поток отказов сложных систем и. т.д.
Замечание. Если в произвольном потоке требований каждое требование отбрасывать с определенной вероятностью, то после такого многократного «прореживания» получается поток близкий к простейшему.
Пример:
Известно, что наборщик в среднем допускает одну ошибку на две страницы текста. В набранной книге взяли наугад страницу. Какова вероятность того, что на данной странице содержится более одной опечатки? Какова вероятность того, что на данных четырех страницах содержится ровно одна опечатка?
Решение:
Опечатки появляются по одной и независимо друг от друга. Условия простейшего потока приблизительно выполняются, и формула Пуассона приблизительно верна. На одну страницу приходится в среднем 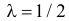 опечатки. Поэтому вероятность того, что на данной странице содержится более одной опечатки, равна
опечатки. Поэтому вероятность того, что на данной странице содержится более одной опечатки, равна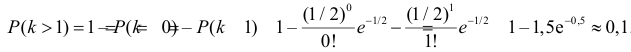 .
.
Для четырех страниц среднее число опечаток 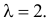 Поэтому
Поэтому 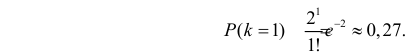
Ответ. 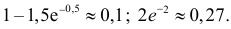
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |