
Произвольная пространственная система сил в теоретической механике
Произвольная пространственная система сил:
Если надо осуществить параллельный перенос силы Р (рис. 112) в любую точку О, то, приложив к точке О две силы Р и —Р, мы замечаем, что данная нам сила Р оказалась перенесенной в точку О, но .зато присоединилась пара сил (Р, — Р), момент которой 
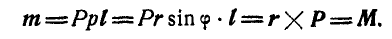
Если имеется п сил, расположенных как угодно в пространстве (рис. 113), то, выбрав произвольную точку О (центр приведения), осуществим параллельный перенос всех сил в точку О.
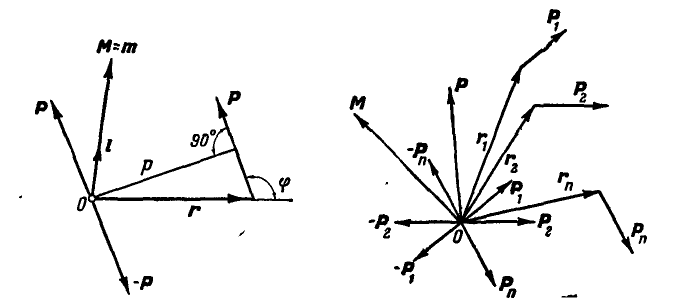
Рис. 112. Рис. 113.
В результате такого переноса заданная нам система сил привелась к системе пар  и к силам
и к силам 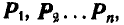 приложенным в точке О. Обозначив момент равнодействующей всех пар через
приложенным в точке О. Обозначив момент равнодействующей всех пар через  , а результирующую сил, приложенных в точке О, через Р, можем написать:
, а результирующую сил, приложенных в точке О, через Р, можем написать:
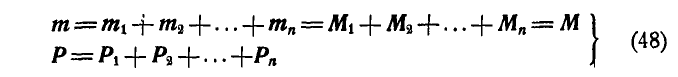
Таким образом, силы, расположенные как угодно в пространстве, при сложении их приводятся, к некоторому моменту 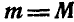 , называемому главным моментом и равному геометрической сумме моментов всех сил относительно центра приведения, и к некоторой силе Р, называемой главным вектором, равной геометрической сумме данных сил.
, называемому главным моментом и равному геометрической сумме моментов всех сил относительно центра приведения, и к некоторой силе Р, называемой главным вектором, равной геометрической сумме данных сил.
Проектируя главный момент и главный вектор на координатные оси, имеем:
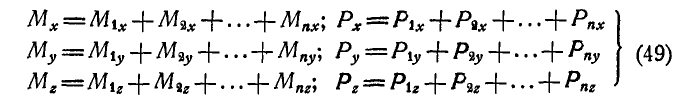
откуда найдем величины главного вектора и главного момента:
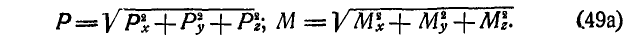
Направление же Р и М определится косинусами углов [см. формулы (6)].
Если бы мы выбрали центр приведения не в точке  , а в какой-либо другой точке
, а в какой-либо другой точке  (рис. 114), то от этого главный вектор не изменится и
(рис. 114), то от этого главный вектор не изменится и 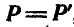 , главный же момент М, вообще говоря, изменится, так как изменятся радиусы-векторы, проведенные из центра моментов к началу каждой силы. Так, для
, главный же момент М, вообще говоря, изменится, так как изменятся радиусы-векторы, проведенные из центра моментов к началу каждой силы. Так, для 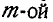 силы новый радиус-вектор
силы новый радиус-вектор 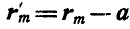 , где
, где 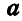 — радиус-вектор, проведенный из старого центра приведения
— радиус-вектор, проведенный из старого центра приведения 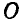 в новый
в новый 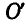 .
.
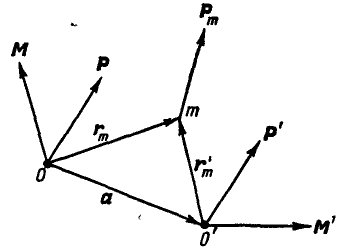
Рис. 114.
Для всех же сил новый главный момент будет:
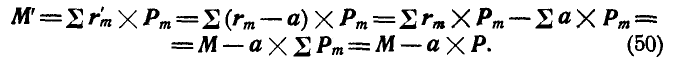
Как постоянный для всех сил, вектор 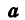 вынесен за знак суммы.
вынесен за знак суммы.
Рассмотрим теперь скалярное произведение 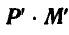 ; имеем:
; имеем:
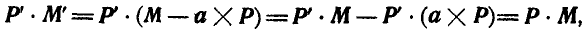
смешанное произведение 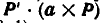 обращается в нуль, так как векторы
обращается в нуль, так как векторы 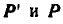 коллинеарны (см. § 1). Отсюда следует, что
коллинеарны (см. § 1). Отсюда следует, что 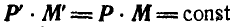 , или
, или 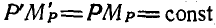 t, откуда
t, откуда 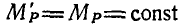 , т. е. проекция главного момента на направление главного вектора для системы сил постоянна и не зависит от выбора центра приведения. Величины, неизменяющиеся при определенных операциях, называются инвариантами. В нашем случае инвариантами по отношению к центру приведения являются главный вектор и проекция главного момента на направление главного вектора или скалярное произведение:
, т. е. проекция главного момента на направление главного вектора для системы сил постоянна и не зависит от выбора центра приведения. Величины, неизменяющиеся при определенных операциях, называются инвариантами. В нашем случае инвариантами по отношению к центру приведения являются главный вектор и проекция главного момента на направление главного вектора или скалярное произведение:
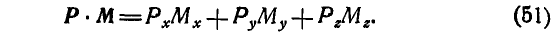
При сложении пространственной системы сил возможны следующие случаи.
1. Если 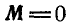 , то силы приводятся к равнодействующей. Следует заметить, что равнодействующая равна и параллельна главному вектору сил. Разница же между равнодействующей сил и их главным вектором заключается в том, что равнодействующая имеет определенное положение линии действия; положение же линии действия главного вектора определяется выбором центра приведения.
, то силы приводятся к равнодействующей. Следует заметить, что равнодействующая равна и параллельна главному вектору сил. Разница же между равнодействующей сил и их главным вектором заключается в том, что равнодействующая имеет определенное положение линии действия; положение же линии действия главного вектора определяется выбором центра приведения.
2. Если 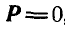 , то силы приводятся к паре.
, то силы приводятся к паре.
3. Если 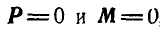 , то силы, расположенные как угодно в пространстве, взаимно уравновешиваются и
, то силы, расположенные как угодно в пространстве, взаимно уравновешиваются и 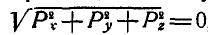 , а также
, а также 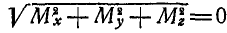 .
.
Следовательно, 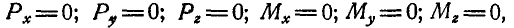 а для этого необходимо, чтобы
а для этого необходимо, чтобы
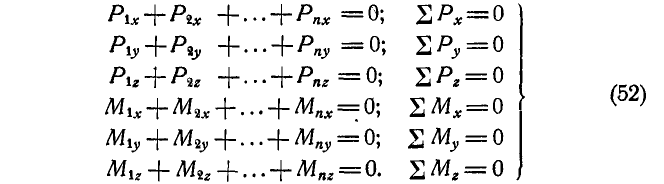
Уравнения (52) называются уравнениями равновесия сил, расположенных как угодно в пространстве.
4. Если 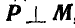 , то силы опять же приводятся к равнодействующей.
, то силы опять же приводятся к равнодействующей.
В самом деле, представляя момент М в виде пары (рис. 115) с силами Р и — Р, замечаем, что силы, приложенные в точке О,. взаимно уравновешиваются и остается только одна равнодействующая сила Р, расположенная от центра приведения на расстоянии 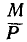 .
.
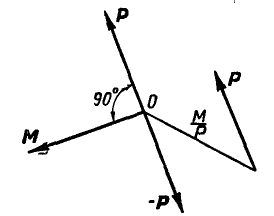
Рис. 115.
Момент полученной равнодействующей относительно центра приведения О равен М, а М, в свою очередь равняется:
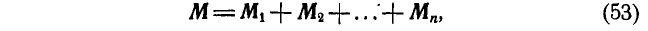
т. е. момент равнодействующей относительно равен геометрической сумме моментов сил составляющих относительно той же точки.
Проектируя равенство (53) на какую-либо ось, например z, имеем:
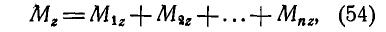
т. е. момент равнодействующей относительно оси z равен алгебраической сумме моментов сил составляющих относительно той же оси.
5. Если 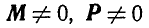 и
и  не
не  , то силы приводятся к динаме.
, то силы приводятся к динаме.
Разложим главный момент М на 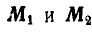 , из которых
, из которых 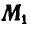 совпадает с
совпадает с  , а
, а  (рис. 116).
(рис. 116).
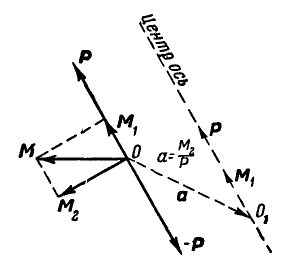
Рис. 116.
Вектор 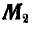 представим в виде пары с силами Р и — Р и плечом
представим в виде пары с силами Р и — Р и плечом 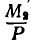 , тогда силы Р и — Р в точке О взаимно уравновешиваются и мы получаем силу Р, проходящую через точку
, тогда силы Р и — Р в точке О взаимно уравновешиваются и мы получаем силу Р, проходящую через точку 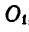 , и момент
, и момент 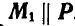 . Перенося момент
. Перенося момент 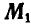 как свободный вектор, в точку
как свободный вектор, в точку 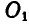 , мы в результате преобразования имеем совокупность векторов — силы Р и момента
, мы в результате преобразования имеем совокупность векторов — силы Р и момента 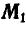 направленных по одной прямой. Эта совокупность называется динамой. Если
направленных по одной прямой. Эта совокупность называется динамой. Если 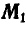 представить в виде пары с плоскостью действия, перпендикулярной к силе Р, то совокупность усилий, получаемых от
представить в виде пары с плоскостью действия, перпендикулярной к силе Р, то совокупность усилий, получаемых от 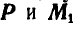 , будет такая же, как и при завинчивании винта, поэтому часто динаму называют винтовым усилием, а линию, вдоль которой направлены векторы Р и
, будет такая же, как и при завинчивании винта, поэтому часто динаму называют винтовым усилием, а линию, вдоль которой направлены векторы Р и 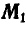 винтовой или центральной осью. Упростить динаму не представляется возможным, поэтому в подобных случаях говорят, что силы, расположенные как угодно в пространстве, приведены к канонической форме.
винтовой или центральной осью. Упростить динаму не представляется возможным, поэтому в подобных случаях говорят, что силы, расположенные как угодно в пространстве, приведены к канонической форме.
Найдем теперь уравнение центральной оси. Мы знаем, что при переходе от одного центра приведения 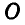 к другому
к другому 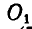 (рис. 114 и 116), главный момент изменится и согласно формуле (50) будет:
(рис. 114 и 116), главный момент изменится и согласно формуле (50) будет: 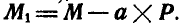
Для того чтобы точка 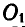 лежала на центральной оси, должно быть выполнено условие
лежала на центральной оси, должно быть выполнено условие  , где
, где 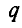 — скалярная величину знак которой определяет одинаковое или противоположное направление векторов
— скалярная величину знак которой определяет одинаковое или противоположное направление векторов 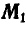 и Р.
и Р.
Далее получим:  . Обозначив координаты радиуса вектора а через х, у и z и принимая во внимание равенства (11), будем иметь:
. Обозначив координаты радиуса вектора а через х, у и z и принимая во внимание равенства (11), будем иметь:
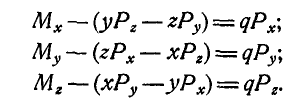
Определяя из каждого полученного равенства 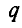 , имеем:
, имеем:
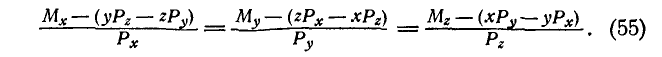
Уравнение (55) и является уравнением центральной оси.
Задача:
Привести к каноническому виду систему трех сил 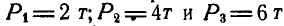 , если силы
, если силы 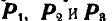 совпадают с ребрами куба, сторона которого равна 1 м (рис. 117).
совпадают с ребрами куба, сторона которого равна 1 м (рис. 117).
Решение. Найдем проекции главного вектора на координатные оси и его величину по формулам (49 и 49а):
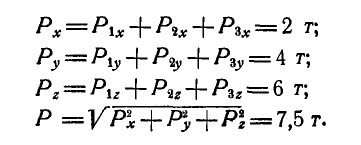
Углы, которые образует главный вектор с осями координат будут:
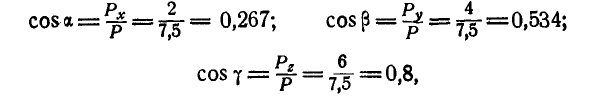
откуда 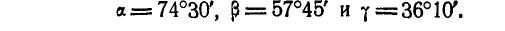
Эти же углы составляет и центральная ось с координатными осями.
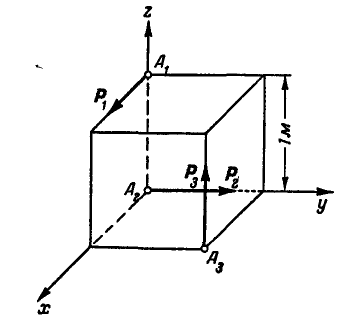
Рис. 117
Проекции главного момента на координатные оси найдутся по равенствам (49):
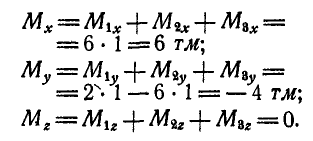
Составляя выражение для инварианта по уравнению (51), получим:
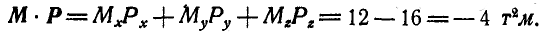
Обозначая проекцию главного момента на направление главного вектора через 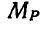 , имеем:
, имеем:
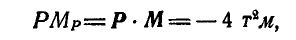
откуда 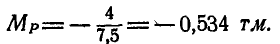
Знак минус у 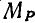 указывает на то, что направления главного момента и главного вектора противоположны. Так как второй инвариант не равен нулю, то система заданных сил приводится к динамическому винту и уравнение центральной оси (55) примет вид:
указывает на то, что направления главного момента и главного вектора противоположны. Так как второй инвариант не равен нулю, то система заданных сил приводится к динамическому винту и уравнение центральной оси (55) примет вид:
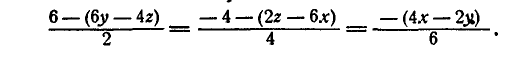
Исключая из первого и второго, а также из второго и третьего уравнений z и у, получим:
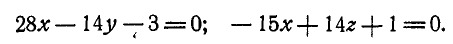
Задача:
Однородный прямоугольный параллелепипед (рис. 119) весом Q= 100 кГ удерживается в равновесии шестью стержнями, па-' раллельными соответствующим ребрам параллелепипеда. Найти усилия  в стержнях 1, 2, 3, 4, 5 и 6 при действии на параллелепипед силы
в стержнях 1, 2, 3, 4, 5 и 6 при действии на параллелепипед силы  , параллельной стержням 1 и 6.
, параллельной стержням 1 и 6.
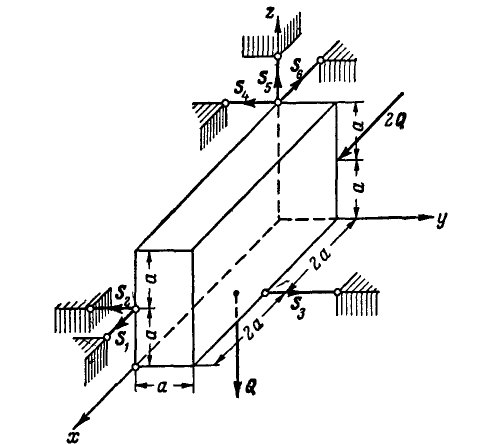
Рис. 119.
Решение. Освободившись от связей (рис. 119), выбираем координатные оси и составляй для параллелепипеда уравнения равновесия (52):
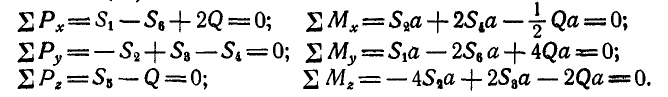
Решая полученные уравнения, имеем:
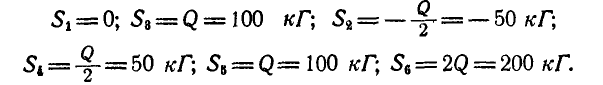
Задача:
Однородный навес ABCD весом Q = 200 кГ наклонен под углом  к горизонтальной плоскости и удерживается в равновесии при помощи шарниров А и В и цепи ED. В точке С приложена вертикальная сила Р = 100 кГ. Определить реакцию шарниров и натяжение цепи Т (рис. 121, а).
к горизонтальной плоскости и удерживается в равновесии при помощи шарниров А и В и цепи ED. В точке С приложена вертикальная сила Р = 100 кГ. Определить реакцию шарниров и натяжение цепи Т (рис. 121, а).
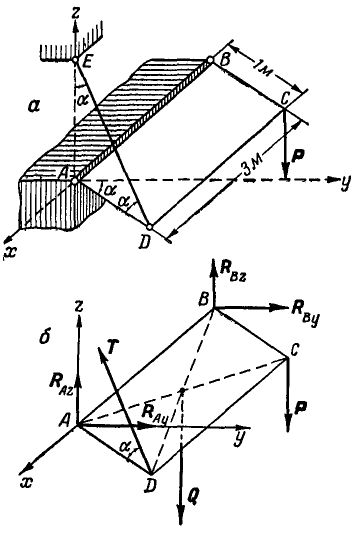
Рис. 121.
Решение. Введем вместо связей их реакции (рис. 121, б)\ тогда по уравнениям (52) получим:
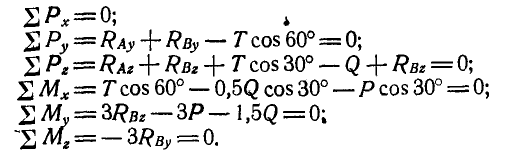
Отсюда находим, что 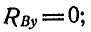

| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Центр параллельных сил и центр тяжести
- Поступательное движение твердого тела
- Вращение твердого тела вокруг неподвижной оси
- Сферическое движение твердого тела
- Расчет ферм
- Пространственная система сходящихся сил
- Момент силы относительно точки и относительно оси
- Теория пар, не лежащих в одной плоскости