
Произвольная плоская система сил в теоретической механике
Содержание:
Произвольная плоская система сил:
Перейдем теперь к сложению сил, расположенных как угодно на плоскости.
Если имеется сила 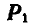
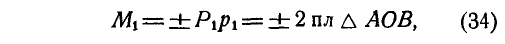
где знак плюс соответствует повороту силой 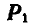 плоскости чертежа вокруг О против часовой стрелки, как показано на рисунке 43, а знак минус — по часовой стрелке.
плоскости чертежа вокруг О против часовой стрелки, как показано на рисунке 43, а знак минус — по часовой стрелке.
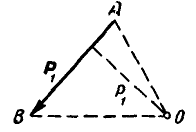
Рис. 43.
Мы уже знаем, что силу, как передвижной вектор, можно переносить по линии ее действия.
Если же мы захотим осуществить параллельный перенос силы 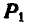 (рис. 44) в положение О, то для этого приложим к точке О две силы
(рис. 44) в положение О, то для этого приложим к точке О две силы 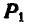 и
и 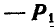 , что допустимо по аксиоме 2. Тогда сила
, что допустимо по аксиоме 2. Тогда сила 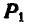 , перечеркнутая на чертеже два раза, является параллельно перенесенной силой, а силы
, перечеркнутая на чертеже два раза, является параллельно перенесенной силой, а силы 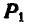 и
и 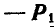 перечеркнутые один раз, образуют присоединенную пару с моментом
перечеркнутые один раз, образуют присоединенную пару с моментом 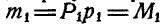 .
.
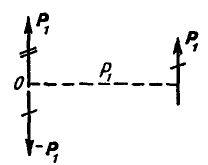
Рис. 44.
Отсюда следует, что при параллельном переносе силы добавляется пара, момент которой равен моменту данной силы относительно точки переноса.
В этом заключается отличие силы как передвижного вектора от свободного вектора, который, как будет показано ниже, по смыслу выражаемой им величины допустимо без дополнительных условий переносить параллельно самому себе.
Если на тело действуют 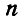 сил
сил 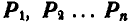 (рис. 45), расположенных как угодно на плоскости, то, осуществив параллельнйй перенос всех сил в произвольно выбранную точку О (центр приведения), мы получим пары с моментами
(рис. 45), расположенных как угодно на плоскости, то, осуществив параллельнйй перенос всех сил в произвольно выбранную точку О (центр приведения), мы получим пары с моментами 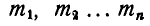 от сил, отчеркнутых один раз, и силы
от сил, отчеркнутых один раз, и силы 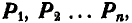 ,
,
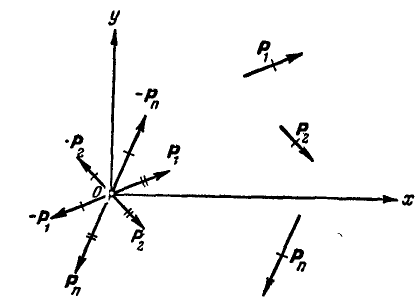
Рис. 45.
приложенные к точке О и отчеркнутые два раза. Если мы обозначим результирующую всех пар через  , а всех сил, приложенных к точке О, через Р, то, согласно равенствам (23) и (32), имеем:
, а всех сил, приложенных к точке О, через Р, то, согласно равенствам (23) и (32), имеем:
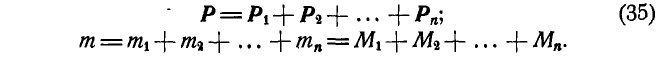
таким образом, силы, расположенные как угодно на плоскости, при сложении их приводятся к силе Р, называемой главным вектором и равной геометрической сумме данных сил, и к паре т, называемой главным моментом, который равен алгебраической сумме моментов всех сил относительно центра приведения.
Величина и направление главного вектора могут быть найдены по формулам (24), (25) и (26).
Рассмотрим случаи, которые могут встретиться при сложении сил, расположенных как угодно на плоскости.
Случай 1. 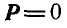 и
и 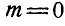 , следовательно силы
, следовательно силы 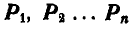 взаимно уравновешиваются, и мы получаем три условия равновесия сил:
взаимно уравновешиваются, и мы получаем три условия равновесия сил:
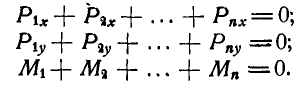
Первые два из этих условий требуют равенства нулю главного вектора, а последнее — главного момента. Полученные аналитические условия называются уравнениями равновесия снл, расположенных как угодно на плоскости, и могут быть записаны более сокращенно:
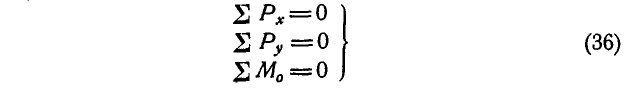
Уравнения (36) могут быть написаны в другой форме, а именно в виде уравнений моментов относительно двух точек А и В и уравнения проекций на какую-либо ось, например х, не перпендикулярную к АВ:
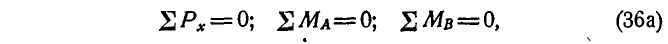
а также в виде уравнений моментов относительно трех точек А, В и С, не лежащих на прямой:
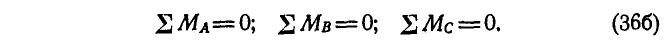
Уравнения (36а) и (36б), выражающие условия равновесия плоской системы сил, легко доказываются. Если Р — равнодействующая плоской системы сил, то для равновесия сил требуется, чтобы момент равнодействующей Р относительно любых двух точек А и В обращался в нуль, а это будет возможно, если линия действия Р проходит через точки А и В. Для равенства же нулю равнодействующей Р дополнительным условием является:
а) равенство нулю проекции равнодействующей на ось, не перпендикулярную к АВ, что приводит нас к уравнениям (36 а),
или
б) равенство нулю ее момента относительно любой точки С, не лежащей на прямой АВ, что приводит нас к уравнениям (36 б).
Следует иметь в виду, что при различных формах записи (36), (36 а), (36 б) число уравнений равновесия сил, приложенных к твердому телу, не может превышать трех. Всякое дополнительное уравнение равновесия, составленное сверх трех, приводит к тождеству.
Случай 2. 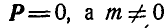 ; следовательно, силы, отчеркнутые два раза, уравновешиваются (рис. 45), и данные силы
; следовательно, силы, отчеркнутые два раза, уравновешиваются (рис. 45), и данные силы 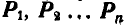 приводятся к паре с моментом
приводятся к паре с моментом 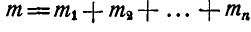 .
.
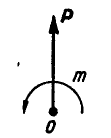
Рис. 46.
Случай 3. 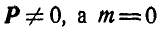 или
или 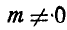 . Если
. Если 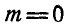 , то данные силы приводятся к равнодействующей силе Р. Если
, то данные силы приводятся к равнодействующей силе Р. Если 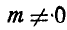 , то для определенности положив
, то для определенности положив 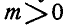 (рис. 46), представим момент
(рис. 46), представим момент 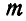 в виде пары с силами
в виде пары с силами 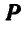 и
и 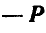 с плечом
с плечом 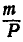 , что возможно (см. § 8, свойство 3). Расположим теперь эту пару так, чтобы одна из сил пары была приложена к точке О и направлена в сторону, противоположную главному вектору Р (рис. 47).
, что возможно (см. § 8, свойство 3). Расположим теперь эту пару так, чтобы одна из сил пары была приложена к точке О и направлена в сторону, противоположную главному вектору Р (рис. 47).
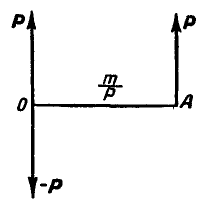
Рис. 47.
Из чертежа видно, что две силы, приложенные в точке О, уравновешиваются, и мы получили одну силу Р, приложенную в точке А.
Отсюда следует, что если 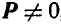 , то силы всегда приводятся к одной равнодействующей. Докажем теперь, что момент равнодействующей относительно любой точки равен алгебраической сумме моментов составляющих относительно той же точки.
, то силы всегда приводятся к одной равнодействующей. Докажем теперь, что момент равнодействующей относительно любой точки равен алгебраической сумме моментов составляющих относительно той же точки.
Действительно, беря момент силы Р относительно выбранной нами ранее произвольно (рис. 47), имеем:
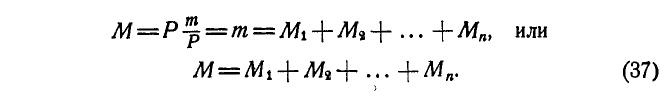
Задача №1
Определить величину и положение линии действия равнодействующей Р системы вертикальных сил, действующих на балку (рис. 48).
Величины сил и размеры указаны на чертеже.
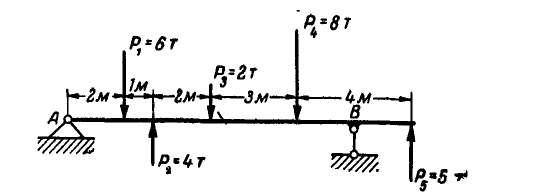
Рис. 48.
Решение. Найдем сначала величину равнодействующей сил:
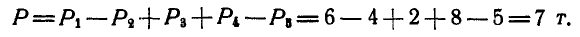
Для нахождения положения равнодействующей обозначим искомое расстояние ее от выбранной нами точки А через р; тогда по формуле (37) имеем:
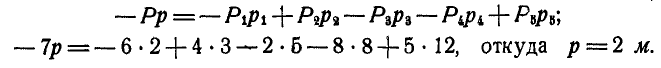
Задача №2
На поршень двигателя диаметром 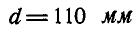 давление р = 15 атм. Определить величину Т касательного усилия, направленного перпендикулярно к кривошипу ОА, и уравновешивающий момент М, приложенный к кривошипу ОА, если известно, что длина кривошипа ОА = г = 6 см и углы, которые составляют кривошип ОА и шатун АВ с прямой ОВ, соответственно равны:
давление р = 15 атм. Определить величину Т касательного усилия, направленного перпендикулярно к кривошипу ОА, и уравновешивающий момент М, приложенный к кривошипу ОА, если известно, что длина кривошипа ОА = г = 6 см и углы, которые составляют кривошип ОА и шатун АВ с прямой ОВ, соответственно равны: 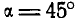 и
и 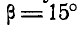 (рис. 49).
(рис. 49).
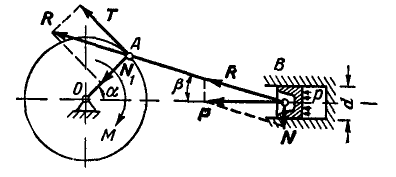
Рис. 49
Решение. Полное давление на поршень:
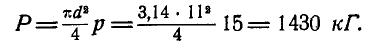
Перенесем силу Р вдоль линии действия в точку В (палец поршня) и разложим ее на две составляющие: силу R, направленную вдоль шатуна, и силу N, направленную перпендикулярно к стенкам цилиндра. Тогда: 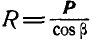 .
.
Перенесем теперь силу R в точку А (палец кривошипа) и разложим ее на две составляющие: силу 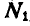 , направленную вдоль кривошипа, и силу Т, перпендикулярную к кривошипу. Тогда касательное усилие будет:
, направленную вдоль кривошипа, и силу Т, перпендикулярную к кривошипу. Тогда касательное усилие будет:
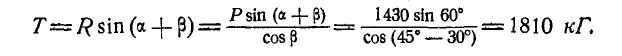
Уравновешивающий момент:
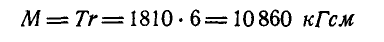
и направлен по направлению часовой стрелки, как показано на рисунке 49.
Задача №3
Однородный брусок АВ весом Q = 200 кГ закреплен в точке В неподвижным шарниром, а в точке С на расстоянии 1/3 длины стержня, считая от точки В, опирается на угол гладкой опоры (рис. 50, а). К концу А бруска приложена горизонтальная сила Р = 400 кГ. Определить реактивные силы в точках С и В.
Решение. Для определения реакций освобождаемся от связей и взамен их вводим силы.
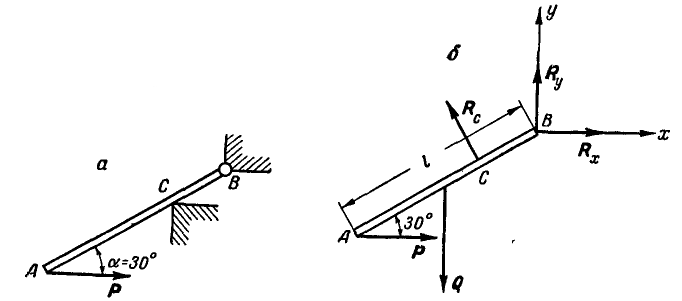
Рис. 50.
Рассмотрим теперь равновесие свободного бруса, находящегося под действием заданных сил Р и Q и реакций, приложенных в точках С и В взамен устраненных связей (рис. 50, б).
Обозначим длину бруса АВ через 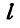 и Проведем через любую точку, например В, координатные оси. Начало координат удобно выбирать в точке схода наибольшего числа неизвестных сил и составлять уравнение моментов сил относительно выбранной точки. Тогда, применяя уравнения (36), имеем:
и Проведем через любую точку, например В, координатные оси. Начало координат удобно выбирать в точке схода наибольшего числа неизвестных сил и составлять уравнение моментов сил относительно выбранной точки. Тогда, применяя уравнения (36), имеем:
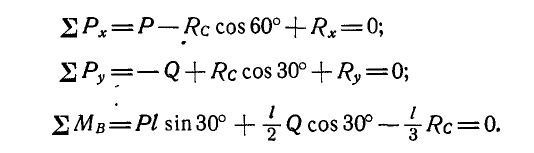
Решая составленные уравнения, получаем:
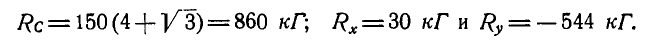
Знак минус у 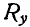 указывает на то, что направление реакции следует изменить на обратное.
указывает на то, что направление реакции следует изменить на обратное.
Задача №4
Однородный брусок ОВ весом Q кГ и длиной 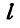 может вращаться вокруг неподвижной точки О (рис. 51, а). К точке В бруска прикреплена нить, перекинутая через малый блок С, а к свободному концу нити подвешен груз Р кГ. Определить величину угла
может вращаться вокруг неподвижной точки О (рис. 51, а). К точке В бруска прикреплена нить, перекинутая через малый блок С, а к свободному концу нити подвешен груз Р кГ. Определить величину угла 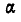 , который составляет стержень ОВ с вертикалью при равновесии, если участок нити СВ горизонтален.
, который составляет стержень ОВ с вертикалью при равновесии, если участок нити СВ горизонтален.
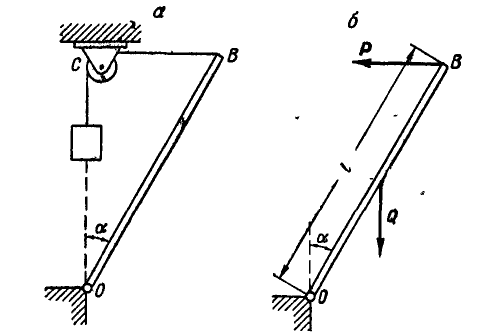
Рис. 51.
Решение. Для определения  а разорвем нить и взамен ее введем силу Р; тогда брусок ОВ будет находиться в равновесии под действием только двух сил Р и Q (рис. 51, б). При наличии оставшейся связи — неподвижного шарнира О — равновесие бруса будет возможно, если он не сможет вращаться вокруг О, а для
а разорвем нить и взамен ее введем силу Р; тогда брусок ОВ будет находиться в равновесии под действием только двух сил Р и Q (рис. 51, б). При наличии оставшейся связи — неподвижного шарнира О — равновесие бруса будет возможно, если он не сможет вращаться вокруг О, а для
этого необходимо, чтобы сумма мойентов всех сил относительно точки О была равна нулю, т. е.
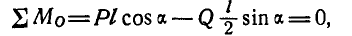
откуда 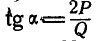 .
.
Задача №5
На ферму (рис. 52) действуют силы 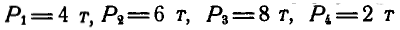 и
и 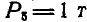 . Найти реактивные силы в шарнирах А и В и усилия
. Найти реактивные силы в шарнирах А и В и усилия 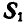 и
и 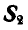 в стержнях
в стержнях 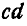 и
и 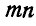 . Все размеры и направления сил показаны на чертеже.
. Все размеры и направления сил показаны на чертеже.
Решение. Определим сначала реакции в шарнирах А к В. Освободившись от связей и проведя через А координатные оси, имеем:
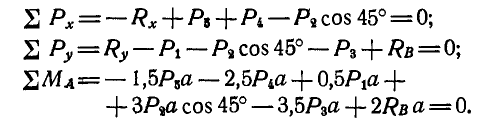
Отсюда находим: 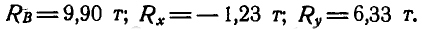
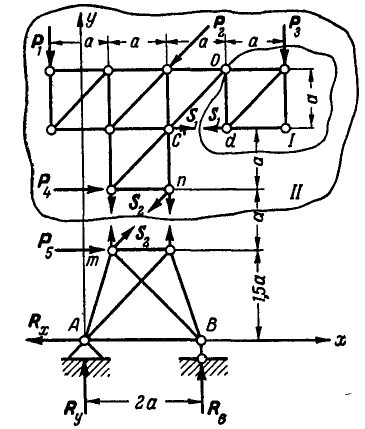
,Рис. 52.
Для определения усилия 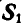 в стержне
в стержне 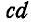 удаляем стержень и взамен его вводим реактивные силы
удаляем стержень и взамен его вводим реактивные силы 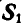 (рис. 52). Теперь часть фермы, ограниченная замкнутым сечением
(рис. 52). Теперь часть фермы, ограниченная замкнутым сечением 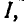 получила возможность вращения вокруг шарнира О, а потому для равновесия этой части необходимо, чтобы
получила возможность вращения вокруг шарнира О, а потому для равновесия этой части необходимо, чтобы
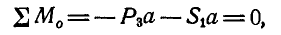
откуда 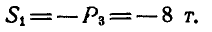
Для определения усилия 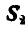 в стержне
в стержне 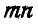 рассмотрим равновесие верхней части фермы, ограниченной замкнутым сечением
рассмотрим равновесие верхней части фермы, ограниченной замкнутым сечением 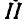 (рис. 52).
(рис. 52).
Проектируя все силы выделенной части на ось х, имеем:
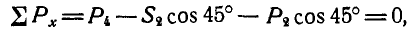
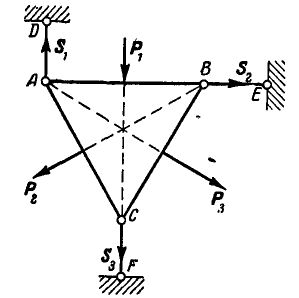
Рис. 53.
Задача №6
Невесомая пластинка АВС, имеющая форму равностороннего треугольника (рис. 53), удерживается в равновесии тремя шарнирными стержнями, из которых два DA и CF вертикальны, а один BE — горизонтальный. На пластинку действуют три направленные по медианам треугольника силы: 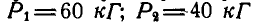 и
и 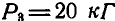 . Найти усилия
. Найти усилия 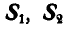 и
и 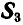 в стержнях DA, BE и CF.
в стержнях DA, BE и CF.
Решение. Освободимся от связей и взамен их введем реактивные силы 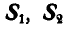 и
и 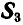 (рис. 53). Обозначая сторону треугольника через
(рис. 53). Обозначая сторону треугольника через 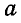 и применяя уравнения равновесия по формуле (36 б), имеем:
и применяя уравнения равновесия по формуле (36 б), имеем:
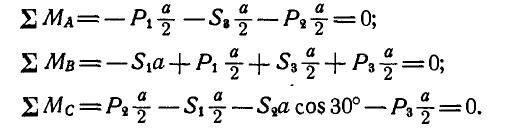
Отсюда 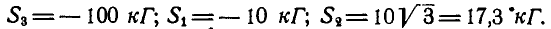
Задача №7
Тело А весом Q = 100 кГ лежит на шерохрватой горизонтальной плоскости ВС, могущей вращаться вокруг шарнира В (рис. 54, а). К плоскости прикладывается момент, который медленно поворачивает плоскость на угол 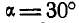 к горизонту. Каково должно быть при этом минимальное значение коэффициента трения, чтобы тело при повороте плоскости осталось в равновесии, и какой, вращающий момент
к горизонту. Каково должно быть при этом минимальное значение коэффициента трения, чтобы тело при повороте плоскости осталось в равновесии, и какой, вращающий момент 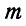 при этом надо приложить.
при этом надо приложить.
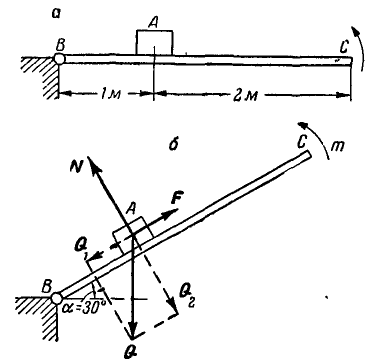
Рис. 54.
Решение. При повороте плоскости на 30° (рис. 54, б) на тело А действуют три силы Q, N и F. Раскладывая вес тела Q на две составляющих 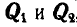 , замечаем, что для равновесия тела А необходимо, чтобы
, замечаем, что для равновесия тела А необходимо, чтобы 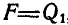 , или так как
, или так как 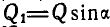 ,
, 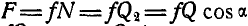 , то
, то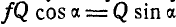 .
.
Отсюда 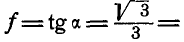
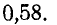
Для того чтобы повернутая плоскость находилась в равновесии, необходимо выполнить условие равенства нулю относительно шарнира В моментов всех сил, действующих на плоскость: 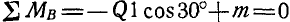 , откуда
, откуда 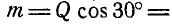
Задача №8
Однородный брусок АВ длиной 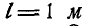 и весом Q кГ опирается свободно своим концом А и в точке С на две шероховатые опоры (рис. 55, а). К концу стержня подвешен груз Р кГ.
и весом Q кГ опирается свободно своим концом А и в точке С на две шероховатые опоры (рис. 55, а). К концу стержня подвешен груз Р кГ.
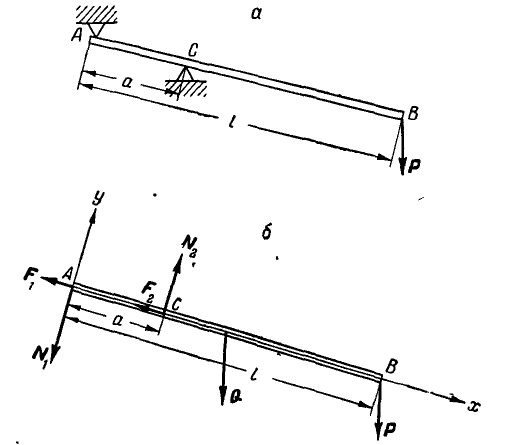
Рис. 55.
На каком расстоянии 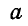 следует расположить опоры, чтобы при
следует расположить опоры, чтобы при  брусок, имеющий наклон в 30°, находился в равновесии?
брусок, имеющий наклон в 30°, находился в равновесии?
Решение. Из рассмотрения равновесия бруска (рис. 55, б) имеем:
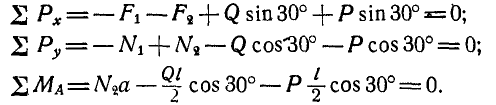
Умножив второе уравнение на 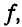 вычтя из него первое уравнение и заменив
вычтя из него первое уравнение и заменив 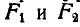 через
через 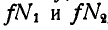 , имеем:
, имеем:
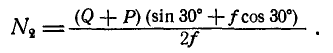
Подставив значение 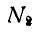 в третье уравнение, получим:
в третье уравнение, получим:
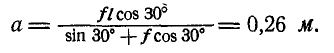
Задача №9
По балке АВ, лежащей на двух опорах, перемещается грузовая каретка, состоящая из грузов 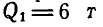 и
и 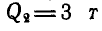 (рис. 56).
(рис. 56).
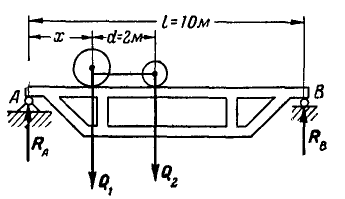
Рис. 56.
Найти расстояние х центра первого колеса от левой опоры А так, чтобы момент опорной реакции  относительно его центра был наибольшим. Каковы опорные реакции в шарнирах А и В при найденном положении груза?
относительно его центра был наибольшим. Каковы опорные реакции в шарнирах А и В при найденном положении груза?
Решение. Балка АВ находится в равновесии под действием заданных сил  и опорных реакций
и опорных реакций  . Определим величину реакции
. Определим величину реакции 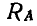 , для чего составим уравнение моментов всех сил относительно точки В:
, для чего составим уравнение моментов всех сил относительно точки В:
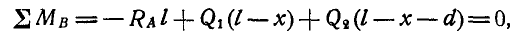
откуда 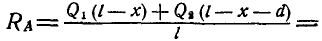
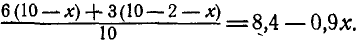
Момент 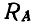 относительно центра первого колеса равен
относительно центра первого колеса равен 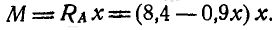
Беря производную по х от этого момента и приравнивание нулю, находим значение х, соответствующее наибольшему моменту:
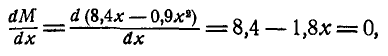
’
Откуда 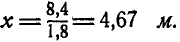 При найденном значении
При найденном значении 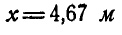 получим:
получим:
Произвольная система сил
Различные случаи приведения произвольной системы сил:
Главный вектор и главный момент относительно начала координат можно вычислить по их проекциям на оси
Как было показано в § 11, всякая система сил, приложенных к твердому телу, может быть приведена к главному вектору (27), приложенному в любой точке тела, равному геометрической сумме всех сил системы, и к главному моменту (28), равному геометрической сумме моментов всех сил относительно той же точки.
Чтобы избежать геометрического суммирования, величину главного вектора можно вычислить через суммы проекций всех сил на три оси координат:
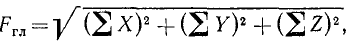 (5)
(5)
а его направление — по трем направляющим косинусам (6).
Если за центр приведения выбрано начало координат, то главный момент системы сил относительно этой точки удобно определять по формуле, аналогичной (22):
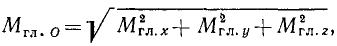 (22/)
(22/)
а главные моменты относительно осей координат — по формулам:
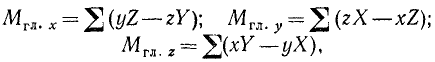 (23/)
(23/)
причем суммирование распространено на все силы.
Заметим, что проекцию главного момента системы сил относительно центра приведения на какую-либо ось, проходящую через этот центр, называют главным моментом системы сил относительно этой оси. Момент силы относительно оси является скаляром второго рода, поэтому главный момент системы относительно оси равен алгебраической сумме моментов всех сил системы относительно этой оси.
Система сил, приложенных к твердому телу, в общем случае эквивалентна динаме, т. е, силе и паре, момент которой параллелен силе
Динамический винт
В произвольной системе сил, как и в плоской, главный вектор является инвариантом, он не зависит от центра приведения, а главный момент зависит от центра приведения. Но система сил, не расположенных в одной плоскости, имеет второй инвариант—проекция главного момента на главный вектор.
Пусть к твердому телу приложена произвольная система сил. Если, приведя такую систему сил к какой-либо точке А (рис. 68, а), мы найдем, что главный вектор и главный момент не равны нулю и не перпендикулярны между собой (общий случай), то мы можем раз-
дожить 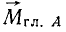 на две составляющие, из которых одна
на две составляющие, из которых одна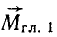 направлена по главному вектору, а другая
направлена по главному вектору, а другая 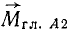 перпендикулярна к нему. Представив
перпендикулярна к нему. Представив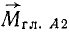 в виде пары сил, модули которой равны модулю главного вектора, а плечо равно
в виде пары сил, модули которой равны модулю главного вектора, а плечо равно 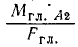 , мы расположим эту пару (рис. 68, б) так, чтобы одна из сил пары уравновесила главный вектор. Данная система сил приведена нами (рис. 68, в) к главному вектору, линию действия которого называют центральной осью системы сил, и к главному моменту
, мы расположим эту пару (рис. 68, б) так, чтобы одна из сил пары уравновесила главный вектор. Данная система сил приведена нами (рис. 68, в) к главному вектору, линию действия которого называют центральной осью системы сил, и к главному моменту 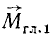 , параллельному главному вектору. Мы можем представить
, параллельному главному вектору. Мы можем представить 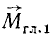 в виде пары сил. Совокупность силы и пары, момент которой параллелен силе, называют динамическим винтом, или динамой. Так как момент пары есть вектор свободный, можно перенести его на центральную ось системы сил (рис. 68, г).
в виде пары сил. Совокупность силы и пары, момент которой параллелен силе, называют динамическим винтом, или динамой. Так как момент пары есть вектор свободный, можно перенести его на центральную ось системы сил (рис. 68, г).
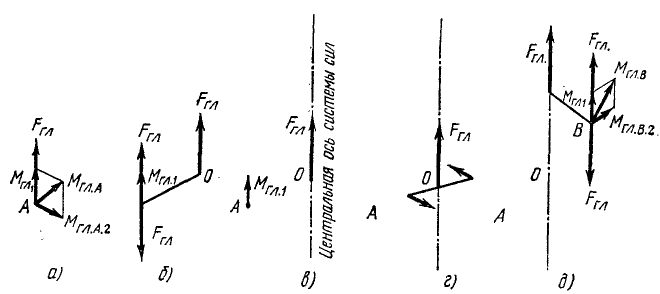
Рис. 68
Таким образом, система сил, приложенных к твердому телу, в общем случае может быть приведена к динамическому винту.
Если бы мы приняли за центр приведения не точку А, а какую-либо другую точку В (рис. 68,6), то получили бы такой же главный вектор (инвариант), приложенный в этой точке В, но иной главный момент 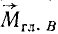 . Раскладывая главный момент на две составляющие (параллельно и перпендикулярно главному вектору), мы получили бы такой же
. Раскладывая главный момент на две составляющие (параллельно и перпендикулярно главному вектору), мы получили бы такой же 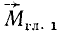 (второй инвариант), но
(второй инвариант), но 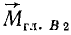 отличался бы от
отличался бы от 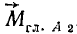 . Представляя
. Представляя 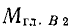 в виде пары сил, мы пришли бы к тому же динамическому винту и с той же центральной осью, так как этот динамический винт эквивалентен данной системе сил и, конечно, не может зависеть от того, какую точку мы выберем за центр приведения. Скалярную величину, характеризующую динамический винт и равную отношению модуля вектора момента
в виде пары сил, мы пришли бы к тому же динамическому винту и с той же центральной осью, так как этот динамический винт эквивалентен данной системе сил и, конечно, не может зависеть от того, какую точку мы выберем за центр приведения. Скалярную величину, характеризующую динамический винт и равную отношению модуля вектора момента 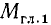 к модулю вектора силы
к модулю вектора силы 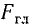 , называют параметром динамического винта.
, называют параметром динамического винта.
Если главный момент перпендикулярен главному вектору, то система сил эквивалентна равнодействующей
Случаи приведения к равнодействующей и к паре. Если, приведя систему к какому-либо центру А, мы обнаружим, что главный вектор и главный момент взаимно перпендикулярны, то система приводится
к одной равнодействующей. В самом деле, положив (рис. 68), что 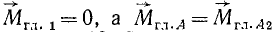 и представив этот момент в виде пары (см. рис. 68, б), силы которой равны главному вектору, мы сведем всю систему к одной силе
и представив этот момент в виде пары (см. рис. 68, б), силы которой равны главному вектору, мы сведем всю систему к одной силе 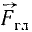 (см. рис. 68, в), т. е. к равнодействующей, направленной вдоль центральной оси, которая в этом случае становится линией действия равнодействующей. Здесь мы имеем случай, аналогичный встреченному нами при приведении плоской системы сил к равнодействующей (см. рис. 51).
(см. рис. 68, в), т. е. к равнодействующей, направленной вдоль центральной оси, которая в этом случае становится линией действия равнодействующей. Здесь мы имеем случай, аналогичный встреченному нами при приведении плоской системы сил к равнодействующей (см. рис. 51).
Понятно, что произвольная система сил также эквивалентна одной равнодействующей и в том случае, если главный момент равен нулю, а главный вектор нулю не равен. В этом случае главный вектор один, без главного момента, эквивалентен системе сил, т. е. является ее равнодействующей, а линия действия равнодействующей проходит через центр приведения.
Если же в результате приведения системы сил к центру окажется, что главный вектор равен нулю, а главный момент нулю не равен, то система эквивалентна паре, момент которой равен главному моменту и (в этом случае) не зависит от центра приведения.
Равновесие системы произвольно расположенных сил
Если главный вектор н главный момент системы сил равны нулю, то система сил находится в равновесии
Случай равновесия
Если и главный вектор системы, и главный момент системы относительно точки приведения равны нулю, то система сил находится в равновесии. Справедливо и обратное заключение: если
данная система сил находится в равновесии, то и главный вектор системы, и главный момент равны нулю.
Следовательно, условия
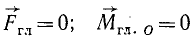 (41)
(41)
являются необходимыми и достаточными условиями равновесия произвольной системы сил.
В случае равновесия системы не только первое из равенств (41), но и второе не зависят от центра приведения. В самом деле, если система находится в равновесии, т. е. если система сил такова, что наличие этой системы эквивалентно ее отсутствию, то это равновесие системы не может нарушиться от того, выберем ли мы за центр приведения ту или иную точку тела.
Равенства (41) называют условиями равновесия произвольной системы сил в геометрической форме. Сравнивая их с полученными ранее условиями (31) равновесия плоской системы сил, мы видим, что различие заключается в том, что в (41) главный момент системы написан как вектор, а в (31) —как скалярная величина. По сути дела равенства (31) являются частным случаем равенств (41), как и плоская система сил является частным случаем системы сил, расположенных произвольно в пространстве.
Напишем условия равновесия в таком виде:
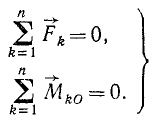 (41')
(41')
Для равновесия произвольной системы сил необходимо и достаточно, чтобы равнялись нулю суммы проекций всех сил на оси координат и суммы моментов всех сил относительно осей координат.
Оба равенства (41') геометрические и выражают условие замкнутости многоугольника сил и многоугольника моментов. Оба эти многоугольника являются не плоскими, а пространственными, поэтому каждая из геометрических сумм векторных величин (41') может быть заменена тремя алгебраическими суммами проекций этих векторов на оси прямоугольной системы координат. Построим прямоугольную систему координат с началом в центре приведения (в любой точке пространства). Спроецировав все силы на эти координатные оси, а также спроецировав на те же оси все векторы моментов сил относительно начала координат, мы заменим два геометрических равенства (41') шестью аналитическими равенствами:
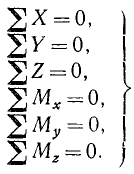 (42)
(42)
Эти равенства называют условиями равновесия произвольной системы сил, выраженными в аналитической форме. Если эти условия содержат неизвестные величины, то их называют уравнениями равновесия произвольной системы сил.
Вместо Mx, My и Mz мы можем подставить их выражения (23) и условия равновесия произвольной системы сил записать в следующем виде;
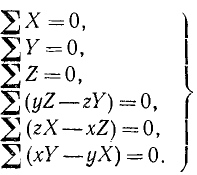 (43)
(43)
Таким образом, для равновесия произвольной системы сил необходимо и достаточно, чтобы равнялись нулю суммы проекций всех сил на три взаимно перпендикулярные оси и суммы моментов всех сил относительно этих осей.
Выведенные ранее условия равновесия системы сил для различных случаев (8), (33), (36) могут быть получены из условий (42) или (43). Так, например, если система сил лежит в плоскости хОу, то аппликаты z точек приложения сил и проекции Z сил на ось Oz равны нулю, третье, четвертое и пятое из равенств (43) тождественно обращаются в нуль, а шестое ввиду равенства (16) будет представлять сумму моментов относительно точки О, и мы получим равенства (33).
Выведем условия равновесия системы параллельных сил, не лежащих в одной плоскости. Построим систему прямоугольных координат, направив ось Oz параллельно линиям действия сил. В таком случае первое, второе и шестое из равенств (42) и (43) обращаются в тождество 0 = 0, остаются лишь третье, четвертое и пятое равенства:
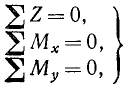 (44)
(44)
являющиеся необходимыми и достаточными условиями равновесия системы параллельных сил, не лежащих в одной плоскости.
Задача о равновесии должна содержать столько же неизвестных, сколько имеется уравнений равновесия для данной системы сил, поэтому в задачах на равновесие системы сил, произвольно расположенных в пространстве, не может быть более шести неизвестных, а задачи на равновесие системы параллельных сил, не лежащих в одной плоскости, могут иметь лишь по три неизвестных, в противном случае это будут статически неопределенные задачи. Так, например, определение реакций в четырех ножках стула является статически неопределенной задачей, так как имеется лишь три уравнения (44) и число неизвестных в задаче больше числа уравнений равновесия.
Задачи на определение равновесия пространственной системы сил решают аналогично задачам на равновесие плоской системы сил. Сначала выделяют твердое тело, равновесие которого надо рассмотреть, потом к этому телу прикладывают все действующие на него заданные в условии задачи и искомые силы (и пары сил), а затем составляют и решают уравнения равновесия.
Пространственные системы сил, приложенные к твердому телу, обычно включают в себя большое количество сил, и для определения неизвестных величин обычно приходится составлять много (до шести) уравнений равновесия. Поэтому при решении задач удобно пользоваться таблицей, как это сделано при решении следующего примера.
Задача №10
Прямоугольная дверь, имеющая вертикальную ось вращения АВ, открыта на угол CAD = 60° и удерживается в этом положении двумя веревками, из которых одна CD перекинута через блок и натягивается грузом P = 32 кГ, другая EF—привязана к точке F пола. Вес двери 64 кГ, ее ширина AC= AD=18 дм, высота АB=24 дм. Пренебрегая трением на блоке, определить натяжение T веревки EF, а также реакции цилиндрического шарнира в точке А и подпятника в точке В (рис. 69, а).
Решение. На дверь действуют следующие силы:
1) вес двери G = 64 кГ, приложенный в середине двери (на пересечении диагоналей);
2) натяжение P = 32 кГ веревки CD, направленное по веревке от точки C к точке D, так как блок меняет направление натяжения веревки, но не меняет его величину;
3) натяжение T веревки EF, направленное по этой веревке;
4), 5), 6) —неизвестная по величине и направлению реакция в подпятнике В, которую разложили на составляющие XВ, YВ, ZВ;
7) и 8) — неизвестная по величине и направлению горизонтальная реакция в подшипнике (в цилиндрическом шарнире А), которую мы разложили на составляющие ХА и YА; вертикальная составляющая ZА заведомо равна нулю, так как шарнир допускает вертикальное перемещение, а следовательно, реакция горизонтальна (рис. 69, б).
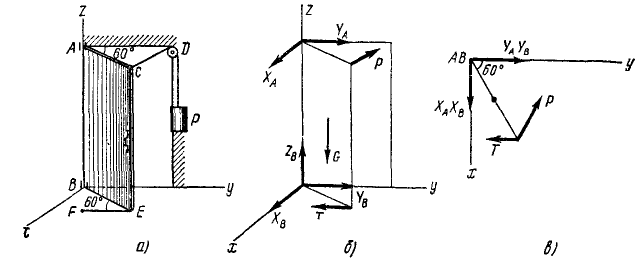
Рис. 69
Выяснив, какие силы действуют на дверь, напишем уравнения равновесия этой системы сил (42) или (43). В данном призере мы воспользуемся формулой (43), для чего составим таблицу, в которую впишем проекции сил и координаты точек приложения сил. Для облегчения этой части решения задачи полезно составить чертеж (рис. 69, в) проекций системы сил на плоскость ху.
Таблица
| № п.п. | силы | Проекция силы | Координаты | Моменты относительно оси | ||||||
| X | Y | Z | x | y | z | Мх=уZ-zY | Мy=zX-xZ | Мх=xY-yX | ||
| 1 | G | 0 | 0 | -64 | 4,5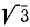 |
4,5 | 12 | -4,5 . 64 = -288 | 4,5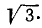 64=498 64=498 |
0 |
| 2 | P | -16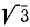 =27,7 =27,7 |
16 | 0 | 9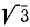 |
9 | 24 | -24 . 16 = -384 | -24. 16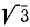 =-664 =-664 |
9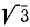 . 16+9 . 16 . 16+9 . 16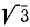 =498 =498 |
| 3 | T | 0 | -T | 0 | 9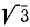 |
9 | 0 | 0 | 0 | -9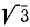 . T=-15,6Т . T=-15,6Т |
| 4 | XB | XB | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | YB | 0 | YB | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | ZB | 0 | 0 | ZB | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | XA | XA | 0 | 0 | 0 | 0 | 24 | 0 | 24 . XA | 0 |
| 8 | YA | 0 | YA | 0 | 0 | 0 | 24 | -24 . YA | 0 | 0 |
Просуммировав третью графу этой таблицы, найдем 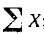 ; просуммировав четвертую графу, найдем
; просуммировав четвертую графу, найдем 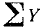 , а пятую—
, а пятую—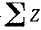 :
:
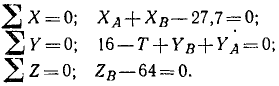
Три последние графы дадут нам три уравнения моментов сил относительно осей координат:
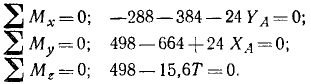
Решая эту систему шести уравнений равновесия, находим шесть неизвестных величин.
Моменты сил относительно координатных осей мы определяли по проекциям этих сил и по координатам точки их приложения, применяя формулы (23). Но их можно определить и иначе — для этого надо спроецировать силу на плоскость, перпендикулярную оси, и затем определить момент проекции силы на плоскость относительно точки пересечения оси и плоскости. Знак момента в таком случае определяют в зависимости от того, поворачивает ли проекция силы свое плечо по ходу часовой стрелки или против хода, если смотреть с положительной стороны оси. Мы рекомендуем читателям определить моменты сил относительно осей в задаче и этим способом.
Решая систему уравнений равновесия, получим положительные значения для всех сил и реакций, кроме YA. Это означает, что на чертеже (см. рис. 69, б) направления сил и реакций взяты правильно, а направление YA надо изменить на противоположное.
Ответ.T = 32 кГ; ХA = 6,9 кГ; YA= —28 кГ; XB = 20,8 κΓ; YB= 44 кГ; ZB=64 кГ.
Определение равнодействующей произвольной плоской системы сил
Произвольную плоскую систему сил можно заменить одной силой — главным вектором — и одной парой сил, момент которой называется главным моментом.
Замену любой плоской системы сил главным вектором и главным моментом необходимо рассматривать как предварительную операцию перед определением равнодействующей силы или равнодействующего момента (пары сил), если система^ не имеет равнодействующей.
Главный вектор по модулю и направлению соответствует геометрической сумме всех данных сил и приложен в произвольно выбранной точке—в центре приведения. Главный момент равен алгебраической сумме моментов всех данных сил относительно точки, в которой приложен главный вектор.
Задачу определения главного вектора и главного момента можно решать как графическим методом, так и аналитическим. Графический метод здесь не рассматривается, а аналитически решение задачи выполняется так:
1) модуль главного вектора 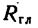
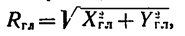
где проекция главного вектора на ось х
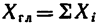
и проекция главного вектора на ось у
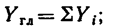
2) направление главного вектора, т. е. углы 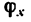 или
или 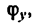 образуемые
образуемые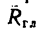 с осями координат, можно определить при помощи тригонометрических соотношений (см. § 4-1, п. 7 настоящего пособия);
с осями координат, можно определить при помощи тригонометрических соотношений (см. § 4-1, п. 7 настоящего пособия);
3) знак и числовое значение главного момента определяются по формуле
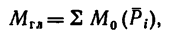
где 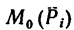 моменты последовательно всех сил относительно одной и той же точки—точки, выбранной для приложения главного вектора — центра приведения.
моменты последовательно всех сил относительно одной и той же точки—точки, выбранной для приложения главного вектора — центра приведения.
В частном случае, как это показано в задачах 60-12 и 61-12, плоскую систему сил можно привести либо только к одной силе — равнодействующей, либо только к одной паре сил- равнодействующему моменту.
Замена главного вектора 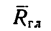 и главного момента
и главного момента 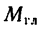 равнодействующей
равнодействующей 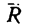 (Е. М. Никитин, § 28) представляет операцию, обратную приведению силы к точке. Приводя силу к любой точке, не расположенной по линии ее действия, получаем силу и пару (Е. М. Никитин, § 25). Теперь необходимо от силы и пары перейти к одной эквивалентной им силе.
(Е. М. Никитин, § 28) представляет операцию, обратную приведению силы к точке. Приводя силу к любой точке, не расположенной по линии ее действия, получаем силу и пару (Е. М. Никитин, § 25). Теперь необходимо от силы и пары перейти к одной эквивалентной им силе.
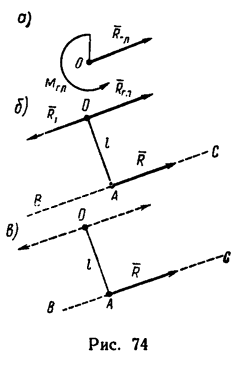
На рис. 74 условно показана последовательность операции замены главных вектора и момента — равнодействующей:
1) на рис. 74, а изображены найденные 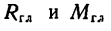 некоторой плоской системы сил;
некоторой плоской системы сил;
2) на рис. 74, б главный момент 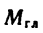 представлен в виде пары
представлен в виде пары 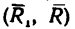 (причем,
(причем, 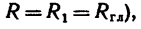 расположенной так, что одна из сил
расположенной так, что одна из сил 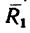 пары уравновешивает главный вектор
пары уравновешивает главный вектор 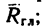
3) уравновешенную систему сил можно убрать и вместо 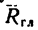 и
и 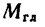 останется одна сила
останется одна сила 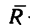 — равнодействующая данной системы сил (рис. 74, в).
— равнодействующая данной системы сил (рис. 74, в).
Таким образом, если плоская система сил приводится к главному вектору и главному моменту, то ее равнодействующая 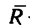 численно и по направлению соответствует главному вектору:
численно и по направлению соответствует главному вектору:
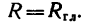
Но линия действия равнодействующей ВС расположена от центра приведения О на расстоянии
Задача №11
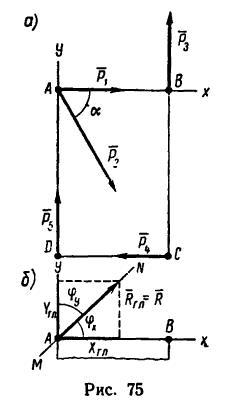
К точкам А, В, С и D, образующим прямоугольник со сторонами ЛВ = 80 см и ВС=180 см, приложены пять сил, как показано на рис. 75, а. Определить главный вектор и главный момент этой системы сил, если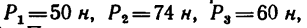
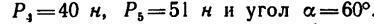 При определении главного момента центр приведения выбрать наиболее рациональным образом.
При определении главного момента центр приведения выбрать наиболее рациональным образом.
Решение.
1. Примем за центр приведения точку А (в этой точке пересекаются линии действия трех сил из пяти) и ее же примем за начало координат, совместив ось х со стороной АВ прямоугольника, а ось у—со стороной DA.
2. Найдем проекции всех заданных сил на ось х:
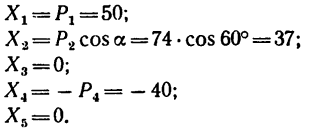
3. Найдем проекции всех заданных сил на ось у:
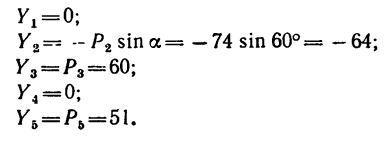
4. Найдем проекции главного вектора на оси х и у. 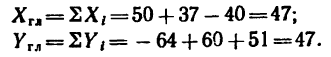
5. Как видно, проекции получаются положительными и равными между собой. Это значит, что главный вектор направлен
под углом 45° к каждой из осей, т. е.
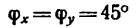
и модуль главного вектора
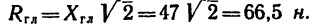
Вектор 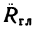 приложен в точке А, принятой за центр приведения (рис. 75, б).
приложен в точке А, принятой за центр приведения (рис. 75, б).
6. Находим главный момент, для этого предварительно определим моменты всех заданных сил относительно центра приведения (точки А);
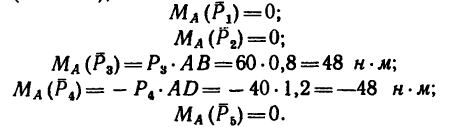
Главный момент
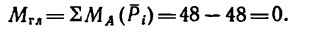
Таким образом, вследствие удачного выбора центра приведения сразу определяется равнодействующая R: ее модуль R = 66,5 н, линия ее действия MN проходит через точку А под углом 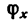 =45° к стороне А В.
=45° к стороне А В.
Если за центр приведения выбрать другую точку, то главный момент не получится равным нулю, кроме тех случаев, когда выбранная точка оказывается на линии действия равнодействующей.
Задача №12
К вершинам квадрата ABCD приложены шесть сил, как показано на рис. 76, а. Сторона квадрата 1 м, модули сил 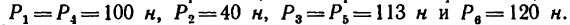
Определить главный вектор и главный момент данной системы сил относительно точки D.
Решение.
1. Поместим начало осей координат в точке D (см. рис. 76, а).
2. Найдем проекции всех сил на ось х:
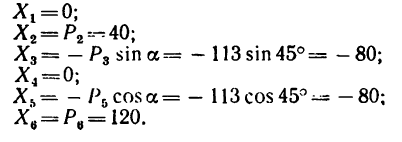
3. Найдем проекции всех сил на ось у:
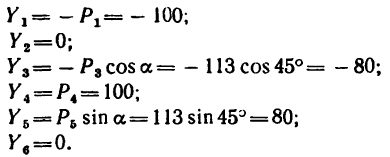
4. Определим проекции главного вектора;
и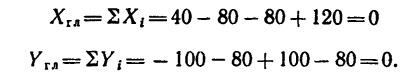
Обе проекции главного вектора равны нулю, значит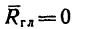 и данную систему сил привести к равнодействующей нельзя.
и данную систему сил привести к равнодействующей нельзя.
5. Найдем главный момент, определив предварительно моменты всех заданных сил относительно центра приведения D. Так как в точке D пересекаются линии действия сил 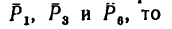
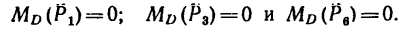
Остается найти моменты лишь трех сил:
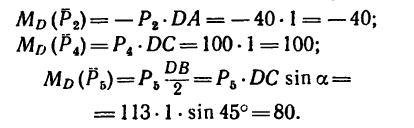
И теперь
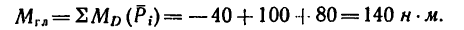
Как видно, система сил приводится к паре сил с моментом (рис. 76, б)
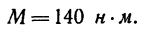
В случае когда главный вектор системы сил равен нулю, центр приведения (центр моментов) при определении главного момента
значения не имеет. Один и тот же результат получим при любом другом центре моментов.
Если в данной задаче при определении главного момента принять за центр моментов, например, точку В, то
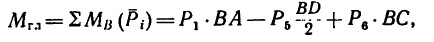
после подстановки числовых значений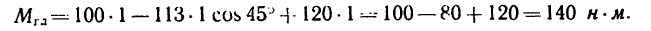
В последней задаче рассмотрена система сил, приводящаяся к паре сил. В связи с этим необходимо обратить внимание на два очень важных свойства пары:
а) алгебраическая сумма проекций сил, составляющих пару, на любую ось равна нулю;
б) алгебраическая сумма моментов сил, образующих пару относительно любой точки, лежащей в плоскости действия пары, есть величина постоянная, равная моменту пары (Е. М. Никитин, § 23).
Действительно, допустим, что на рис. 76 имеются только две силы 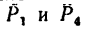 (причем
(причем 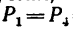 =!00 н). При любом расположении осей х и у
=!00 н). При любом расположении осей х и у
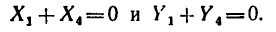
(Рекомендуется проверить самостоятельно справедливость этих равенств при расположении осей, заданном на рис. 76, а также совместив оси х и у с диагоналями квадрата ABCD.) При любом положении центра моментов
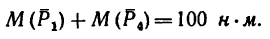
(Рекомендуется проверить и это равенство, приняв за центр моментов любую из точек А, В, С, D или точку пересечения диагоналей квадрата, или любую другую.)
Именно поэтому пара сил, действующая на тело, обычно задается в виде момента и изображается круговой стрелкой, показывающей направление действия момента.
Отмеченные Здесь Свойства пары постоянно используются при составлении уравнений равновесия в задачах:
- а) при составлении уравнений проекций силы, образующие пару, не учитываются (сумма их проекций всегда равна нулю);
- б) при составлении уравнений моментов момент пары сил входит в уравнение независимо от того, где выбран центр моментов.
Задача №13
К четырем точкам тела, образующим квадрат ABCD со стороной 1,2 м приложены силы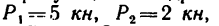
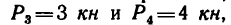 как показано на рис. 77, а. Определить равнодействующую этой системы сил.
как показано на рис. 77, а. Определить равнодействующую этой системы сил.
Решение.
1. За центр приведения примем точку А. Оси координат совместим со сторонами АВ и AD квадрата ABCD (рис. 77, а).
2. Найдем проекции сил на ось х:
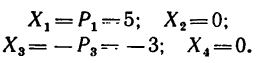
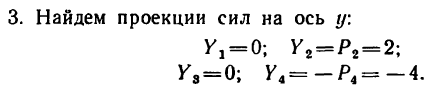
4. Найдем проекции главного вектора на оси х и у:
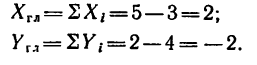
5. Найдем главный вектор. Обе проекции численно равны друг другу. Значит модуль главного вектора
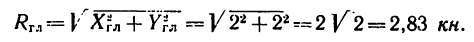
Так как проекция на ось х положительна, а на ось у отрицательна, то главный вектор расположен в четвертом координатном углу и делит его своей линией действия пополам, т. е. угол, образуемый 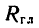 с положительным направлением оси х,
с положительным направлением оси х,
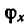 =— 45° (рис. 77, б).
=— 45° (рис. 77, б).
6. Найдем главный момент. Так как относительно точки А (центра приведения) моменты сил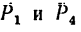 равны нулю, то
равны нулю, то
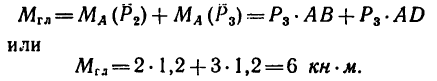
Направление действия главного момента показано на рис. 77, б круговой стрелкой.
7. Заменим  равнодействующей силой R.
равнодействующей силой R.
Известно, что 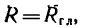 а это значит, что их модули равны
а это значит, что их модули равны 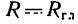 — 2,83 кн, линии действия обоих векторов параллельны, а векторы направлены в одну и ту же сторону. Нужно найти лишь расстояние между центром приведения и линией действия равнодействующей.
— 2,83 кн, линии действия обоих векторов параллельны, а векторы направлены в одну и ту же сторону. Нужно найти лишь расстояние между центром приведения и линией действия равнодействующей.
Это расстояние
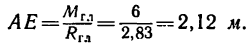
Отрезок АЕ отложим перпендикулярно к направлению 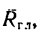 причем в такую сторону, чтобы приложенная к точке Е равнодействующая сила
причем в такую сторону, чтобы приложенная к точке Е равнодействующая сила 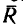 стремилась повернуть АЕ в направлении действия главного момента.
стремилась повернуть АЕ в направлении действия главного момента.
Таким образом, равнодействующая данных четырех сил численно равна 2,83 кн, направлена перпендикулярно к диагонали АС и линия ее действия находится от вершины А квадрата на расстоянии AE' — 2,12 м.
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |