
Производящие функции в теории вероятностей - определение и вычисление с примерами решения
Производящие функции:
Пусть дискретная случайная величина Х имеет закон распределения 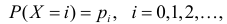
Функция
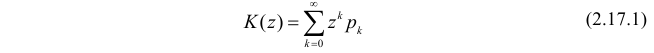
называется производящей функцией этого распределения.
Заметим, что 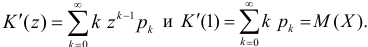
Напомним:
1) Начальным моментом порядка  называется математическое ожидание
называется математическое ожидание 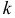 -й степени случайной величины
-й степени случайной величины

Само математическое ожидание является начальным моментом первого порядка.
2) Центральным моментом 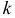 -го порядка называется математическое ожидание
-го порядка называется математическое ожидание 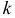 -й степени соответствующей центрированной случайной величины
-й степени соответствующей центрированной случайной величины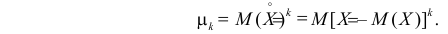
Дисперсия является центральным моментом второго порядка 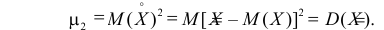
3) Асимметрией распределения называется отношение центрального момента третьего порядка к кубу среднего квадратического отклонения случайной величины: 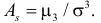
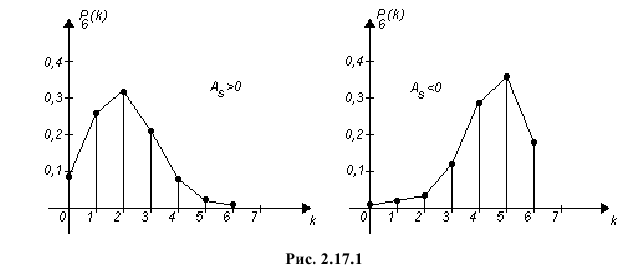
Если распределение симметрично, то 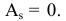 На рис. 2.17.1 слева (в качестве примера закона равпределения с положительной асимметрией) изображен многоугольник распределения для биномиального закона распределения при
На рис. 2.17.1 слева (в качестве примера закона равпределения с положительной асимметрией) изображен многоугольник распределения для биномиального закона распределения при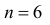 и
и 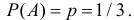 В правой части рис. 2.17.1 приведен пример закона распределения с отрицательной асимметрией (биномиальный закон при
В правой части рис. 2.17.1 приведен пример закона распределения с отрицательной асимметрией (биномиальный закон при  и
и 
4) Для нормального закона распределения 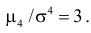 Безразмерный коэффициент
Безразмерный коэффициент 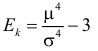 называется эксцессом. Этот коэффициент характеризует «островерхость» распределения в сравнении с нормальным законом распределения. Например, если говорить о функциях плотности вероятности, то при
называется эксцессом. Этот коэффициент характеризует «островерхость» распределения в сравнении с нормальным законом распределения. Например, если говорить о функциях плотности вероятности, то при 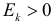 график функции плотности вероятности более островерхий, чем график кривой нормального распределения (см. левую часть рис 2.17.2). При
график функции плотности вероятности более островерхий, чем график кривой нормального распределения (см. левую часть рис 2.17.2). При 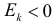 график плотности вероятности имеет более плоскую вершину, нежели нормальная кривая при тех же математическом ожидании и дисперсии (см. правую часть рис. 2.17.2).
график плотности вероятности имеет более плоскую вершину, нежели нормальная кривая при тех же математическом ожидании и дисперсии (см. правую часть рис. 2.17.2).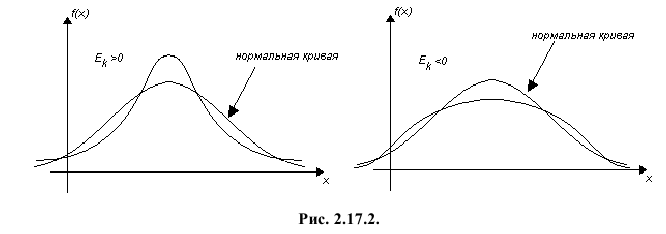
Через производящую функцию можно выразить и другие начальные и центральные моменты случайной величины. Выразим через производящую функцию, например, дисперсию. Так как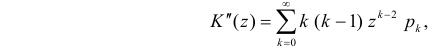
то
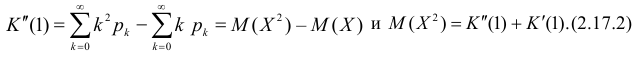
Сформируем в правой части последнего равенства дисперсию. Для этого прибавим и отнимем квадрат математического ожидания: 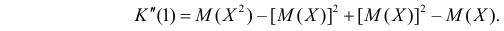
Величина 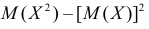 равна дисперсии. Поэтому
равна дисперсии. Поэтому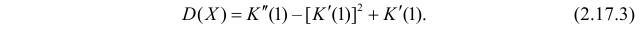
Аналогично
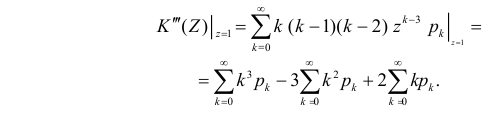
Итак, при z =1 имеем
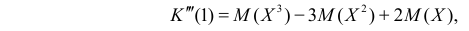
откуда
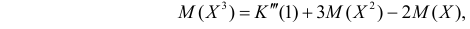
а с учетом (2.17.2) 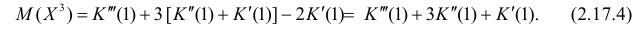
Пусть 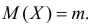 Рассмотрим модифицированную производящую функцию
Рассмотрим модифицированную производящую функцию 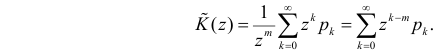
С помощью этой функции можно вычислять сразу центральные моменты случайной величины. Например
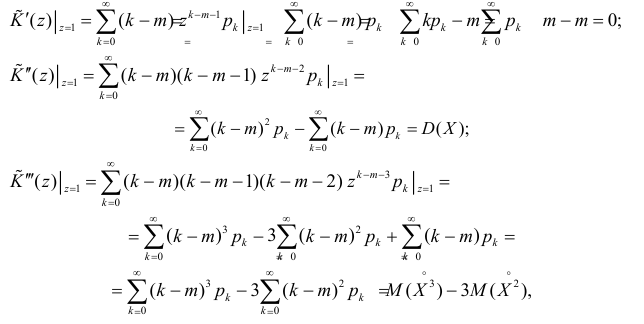
откуда
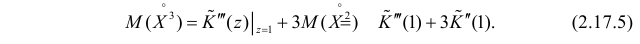
Пример:
Пусть Х имеет пуассоновский закон распределения: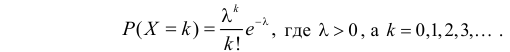
Требуется найти математическое ожидание, дисперсию и коэффициент асимметрии этой случайной величины.
Решение. Производящая функция пуассоновского распределения имеет вид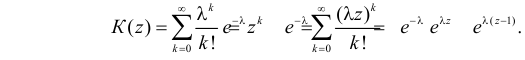
Заметим, что 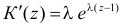 и
и  Поэтому
Поэтому 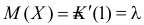 и, в соответствии с (2.17.3),
и, в соответствии с (2.17.3),
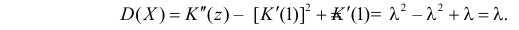
Для вычисления коэффициента асимметрии составим модифицированную производящую функцию. Так как 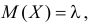 то
то 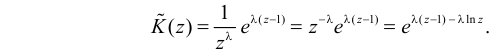
Тогда
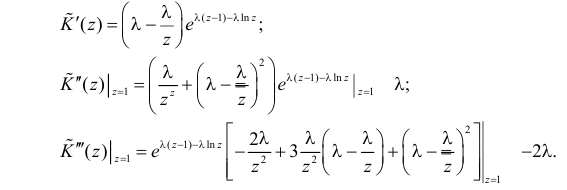
Поэтому по формуле (2.17.5) имеем 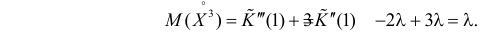
В итоге 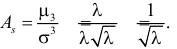
Ответ. 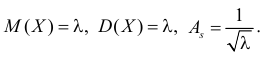
Пример:
Пусть Х имеет закон распределения
(Это частный случай отрицательного биномиального распределения или распределения Паскаля с параметрами 2 и 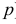 ). Требуется найти
). Требуется найти 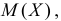
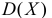 и коэффициент асимметрии
и коэффициент асимметрии 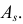
Решение. Составим производящую функцию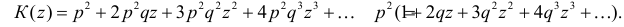
Для вычисления суммы ряда в скобке рассмотрим сумму ряда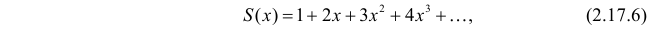
который абсолютно сходится при 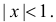 Легко видеть, что нас интересует
Легко видеть, что нас интересует 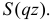 Проинтегрируем почленно ряд (2.17.6) внутри его области сходимости:
Проинтегрируем почленно ряд (2.17.6) внутри его области сходимости: 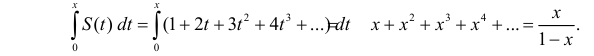
В последней строке мы воспользовались формулой суммы бесконечной убывающей прогрессии:
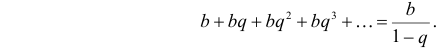
Отсюда 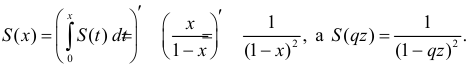 Откуда
Откуда 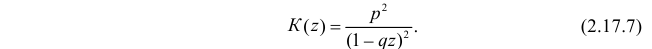
Воспользуемся теперь производящей функцией (2.17.7) для вычисления числовых характеристик случайной величины X:
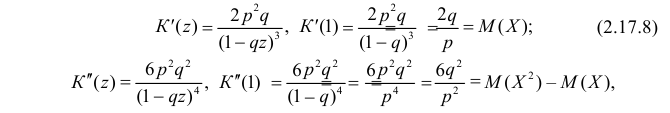
откуда следует, что 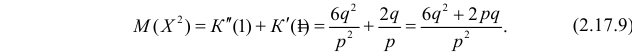
По формуле (2.17.3)
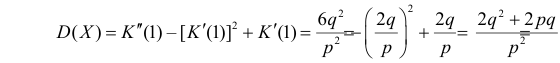
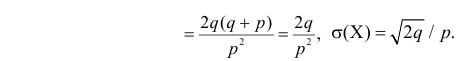
Далее
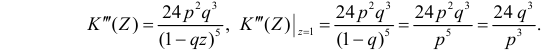
По формуле (2.17.4) вычисляем 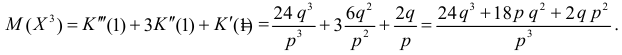
Так как
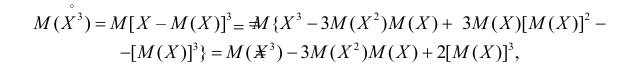
то с учетом (2.17.8) и (2.17.9) имеем
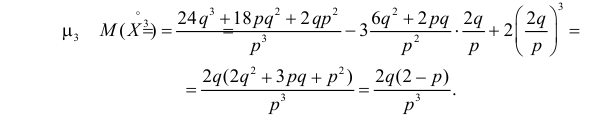
Учитывая это получаем значение коэффициента асимметрии 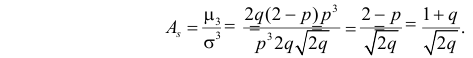
Ответ. 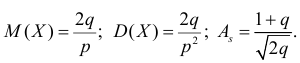
Преобразование Лапласа
Для непрерывной и неотрицательной случайной величины роль производящей функции может играть преобразование Лапласа.
Пусть Х – непрерывная, неотрицательная случайная величина с функцией распределения 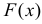 . Тогда
. Тогда 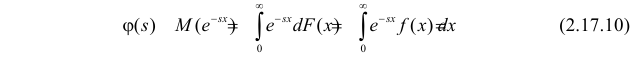
называется преобразованием Лапласа для этого распределения. (Фактически роль величины z в формуле (2.17.1) играет величина 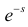 . Преимущество такого выбора состоит в том, что
. Преимущество такого выбора состоит в том, что 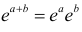 .)
.)
Отметим, что 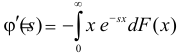 и
и 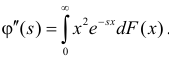 Поэтому
Поэтому 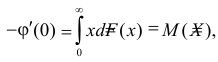 а
а 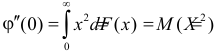 и
и 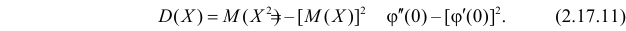
Производная любого порядка от преобразования Лапласа связана с начальными моментами случайной величины соотношением 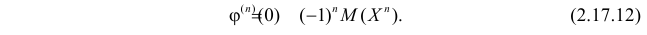
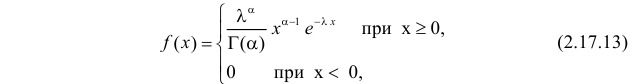
где 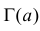 – так называемая гамма-функция Эйлера, которая при целых положительных a принимает значения
– так называемая гамма-функция Эйлера, которая при целых положительных a принимает значения 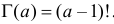
Пример:
Случайная величина X имеет функцию плотности вероятности
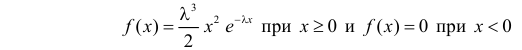
(гамма-распределение с параметрами 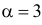 и
и 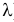 ). Требуется найти
). Требуется найти 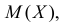
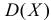 и коэффициент асимметрии
и коэффициент асимметрии 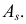
Решение. Соответствующее преобразование Лапласа имеет вид 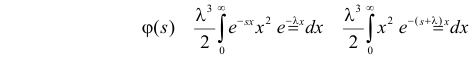
(интегрируем по частям)
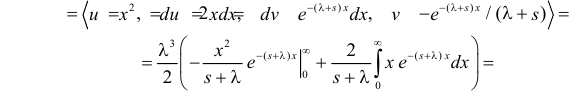
(первое слагаемое в скобке равно нулю, так как 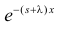 с увеличением
с увеличением 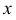 убывает быстрее, чем растет
убывает быстрее, чем растет 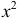 )
)
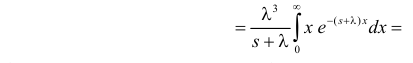
(интегрируем еще раз по частям)
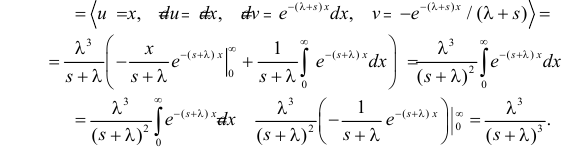
Вычислим начальные моменты распределения:


поэтому
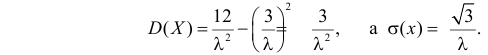
Далее
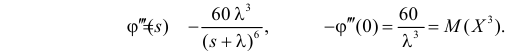
Вычислим центральный момент третьего порядка: 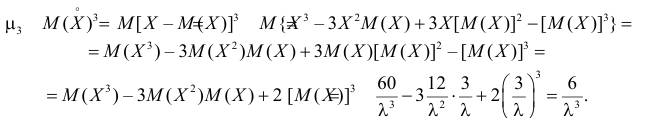
Поэтому
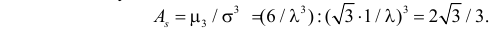
Ответ. 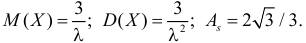
Пример:
Пусть 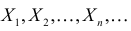 – последовательность независимых неотрицательных одинаково распределенных случайных величин с функцией плотности вероятности
– последовательность независимых неотрицательных одинаково распределенных случайных величин с функцией плотности вероятности 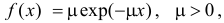
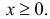 И пусть N – неотрицательная целочисленная случайная величина, независящая от величин
И пусть N – неотрицательная целочисленная случайная величина, независящая от величин 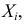 и имеющая пуассоновский закон распределения с параметром
и имеющая пуассоновский закон распределения с параметром 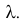 Для случайной величины
Для случайной величины 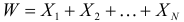 требуется найти
требуется найти 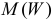 и
и 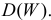
Решение. Производящая функция пуассоновского закона распределения равна 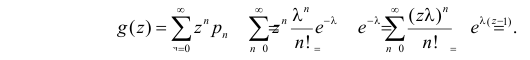
Преобразование Лапласа показательного распределения равно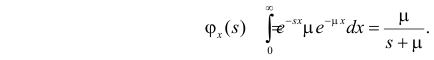
Поэтому по формуле (2.17.14) имеем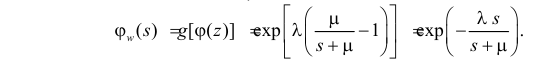
Так как 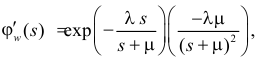 а
а 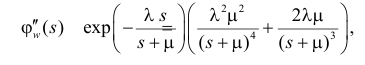
то
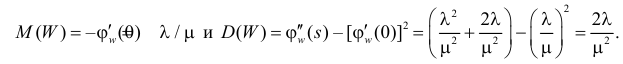
Ответ. 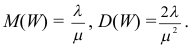
Характеристические функции
Замена z на 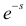 в определении производящей функции позволила рассматривать непрерывные неотрицательные величины. Выгода от такой замены состоит в мультипликативном свойстве:
в определении производящей функции позволила рассматривать непрерывные неотрицательные величины. Выгода от такой замены состоит в мультипликативном свойстве: 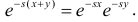 Таким же свойством обладает и показательная функция чисто мнимого аргумента, которая для действительных x определяется равенством:
Таким же свойством обладает и показательная функция чисто мнимого аргумента, которая для действительных x определяется равенством:

Характеристической функцией 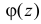 случайной величины X называется комплексно-значная функция, определенная при
случайной величины X называется комплексно-значная функция, определенная при 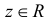 соотношением
соотношением
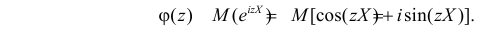
Если 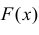 – функция распределения случайной величины X, то
– функция распределения случайной величины X, то 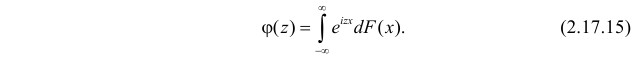
Существование интеграла, определяющего характеристическую функцию, вытекает из непрерывности функции 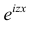 и ее ограниченности:
и ее ограниченности: 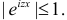 Для дискретной случайной величины X с возможными значениями
Для дискретной случайной величины X с возможными значениями 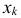 и их вероятностями
и их вероятностями 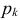 запись (2.17.15) расшифровывается как
запись (2.17.15) расшифровывается как 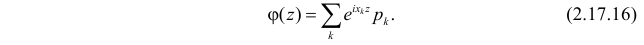
Для непрерывной случайной величины X с функцией плотности вероятности 
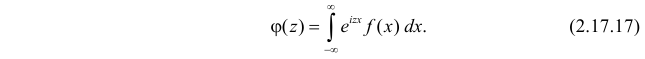
Пример:
Пусть случайная величина X имеет пуассоновский закон распределения, т.е.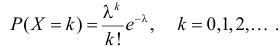 Тогда по формуле (2.17.11)
Тогда по формуле (2.17.11)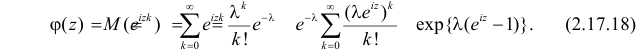
Пример:
Пусть 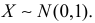 Тогда в соответствии с формулой (2.17.12)
Тогда в соответствии с формулой (2.17.12) 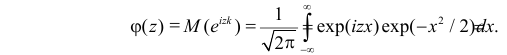
Вместо непосредственного вычисления интеграла, которое требует специальной математической техники, найдем его величину косвенным способом. Заметим, что
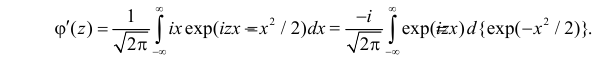
Полученный интеграл берем по частям, полагая 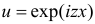 и
и 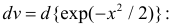
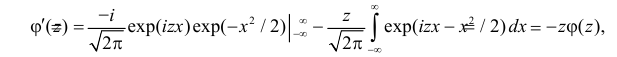
(первое слагаемое равно нулю так как 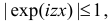 а
а 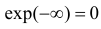 ).
).
В итоге для искомой характеристической функции получаем уравнение, которое при начальном условии 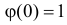 имеет решение
имеет решение 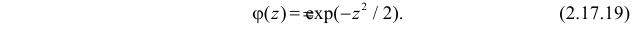
Подобным же образом можно показать, что закон распределения 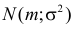 имеет характеристическую функцию
имеет характеристическую функцию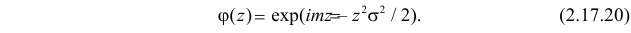
Свойства характеристических функций.
1. 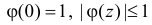 для всех вещественных
для всех вещественных 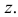
2. Если существует 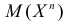 – момент порядка
– момент порядка 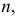 то функция
то функция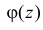 имеет
имеет 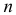 непрерывных производных и
непрерывных производных и

3. Пусть 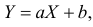 где
где 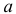 и
и 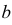 – постоянные величины, а X имеет характеристическую функцию
– постоянные величины, а X имеет характеристическую функцию 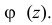 Тогда характеристическая функция случайной величины Y имеет вид
Тогда характеристическая функция случайной величины Y имеет вид 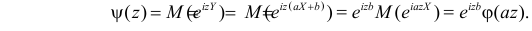
4. Характеристическая функция однозначно определяет распределение случайной величины.
5. Если X1 и X2 – независимые случайные величины, а 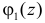 и
и 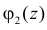 – их характеристические функции, то характеристическая функция суммы
– их характеристические функции, то характеристическая функция суммы 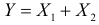 равна произведению характеристических функций слагаемых:
равна произведению характеристических функций слагаемых:
Это следует из того, что в силу независимости слагаемых 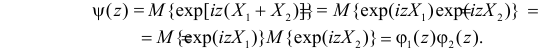
Можно показать, что для любого конечного числа независимых случайных величин 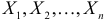 характеристическая функция их суммы
характеристическая функция их суммы 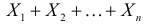 равна произведению характеристических функций слагаемых.
равна произведению характеристических функций слагаемых.
Пример:
Случайные величины X и Y независимы и имеют пуассоновские законы распределения с параметрами 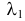 и
и 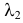 соответственно:
соответственно: 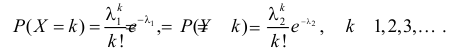
Требуется найти закон распределения случайной величины 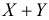 .
.
Решение. Согласно формуле (2.17.18) характеристические функции случайных величин X и Y имеют вид: 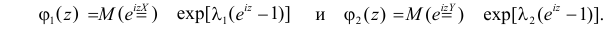
Сумме независимых случайных величин соответствует произведение характеристических функций слагаемых. Поэтому 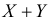 имеет характеристическую функцию
имеет характеристическую функцию 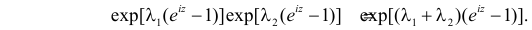
Ответ. 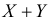 имеет пуассоновский закон распределения с параметром
имеет пуассоновский закон распределения с параметром 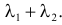
Полученный результат известен как факт устойчивости пуассоновского закона распределения. Этот результат можно обобщить на сумму любого конечного числа пуассоновских случайных величин.
Теорема. Если случайные величины Х1 и Х2 независимы и имеют соответственно нормальные законы распределения 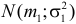 и
и 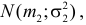 то их сумма
то их сумма 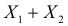 имеет тоже нормальный закон распределения
имеет тоже нормальный закон распределения

Доказательство. Пусть 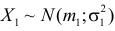 и
и 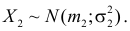 Их характеристические функции в соответствии с формулой (2.17.15) имеют вид
Их характеристические функции в соответствии с формулой (2.17.15) имеют вид 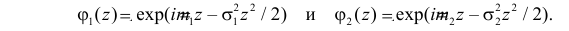
Тогда характеристическая функция суммы  :
: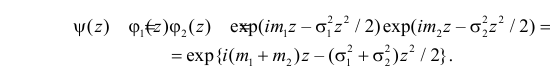
А это и означает, что 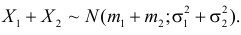
Пример:
Случайная величина 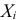 имеет закон распределения.
имеет закон распределения.
Требуется найти характеристическую функцию этой случайной величины. Используя свойства характеристических функций, найти характеристическую функцию случайной величины 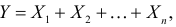 полагая слагаемые независимыми. Используя запись характеристической функции, найти
полагая слагаемые независимыми. Используя запись характеристической функции, найти 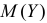 и
и 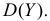
Решение. По формуле (2.17.16)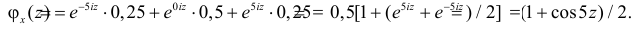
Поэтому характеристическая функция случайной величины Y имеет вид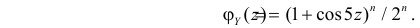
Для вычисления 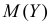 находим
находим 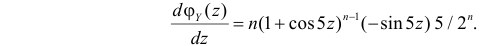
Последнее выражение при 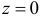 равно нулю. По свойству 2 это означает, что
равно нулю. По свойству 2 это означает, что 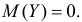 Так как вторая производная характеристической функции по z равна
Так как вторая производная характеристической функции по z равна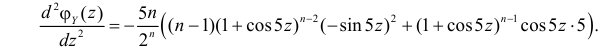
при 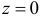 равна
равна 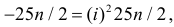 то из свойства 2 следует, что
то из свойства 2 следует, что 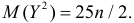 Поэтому
Поэтому
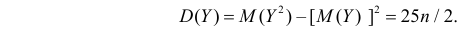
Ответ. 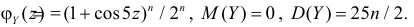
Пример:
Требуется найти характеристическую функцию случайной величины 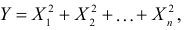 где все
где все 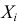 имеют закон распределения
имеют закон распределения 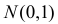 независимы в совокупности. С помощью характеристической функции найти
независимы в совокупности. С помощью характеристической функции найти 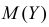 и
и 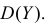
Решение. Найдем сначала характеристическую функцию для 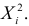 В соответствии с формулой (2.17.7)
В соответствии с формулой (2.17.7)
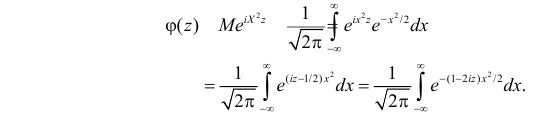
После замены переменных 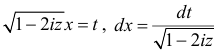 получаем
получаем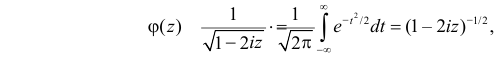
так как 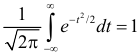 Из свойства 5 характеристических функций следует, что случайная величина
Из свойства 5 характеристических функций следует, что случайная величина 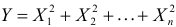 имеет характеристическую функцию
имеет характеристическую функцию
Для вычисления числовых характеристик случайной величины Y найдем сначала первую и вторую производные характеристической функции при 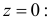
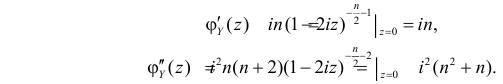
Это означает, что 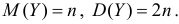
Ответ. 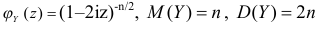
Пример:
Случайная величина Х имеет функцию плотности вероятности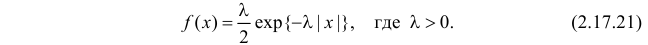
Требуется найти характеристическую функцию этой случайной величины и ее 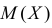 и
и 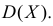 Требуется также найти характеристическую функцию случайной величины
Требуется также найти характеристическую функцию случайной величины 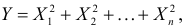 где величины
где величины 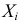 независимы и имеют распределение (2.17.21).
независимы и имеют распределение (2.17.21).
Решение. Найдем сначала характеристическую функцию: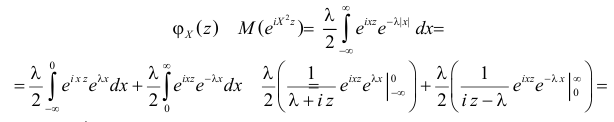
(так как 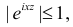 то равенство можно продолжить следующим образом)
то равенство можно продолжить следующим образом)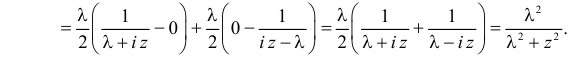
Тогда 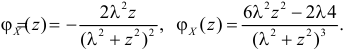 Откуда
Откуда 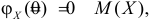
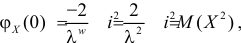 поэтому
поэтому 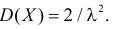
Характеристическая функция случайной величины 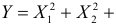
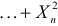 имеет вид:
имеет вид: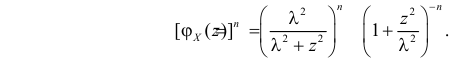
Ответ. 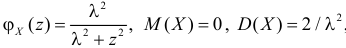
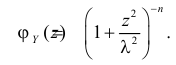
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Теоремы теории вероятностей
- Основные законы распределения дискретных случайных величин
- Непрерывные случайные величины
- Закон больших чисел
- Центральная предельная теорема
- Ковариация в теории вероятности
- Функциональные преобразования двухмерных случайных величин
- Правило «трех сигм» в теории вероятности