
Производные высших порядков - определение и вычисление с примерами решения
Определение: Пусть функция y=f(x) дифференцируема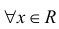
Пример:
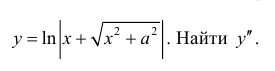
Решение:
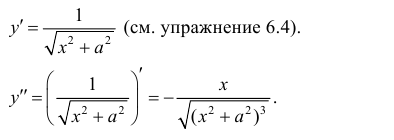
Пример:
Найти k-ю производную функции 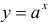 .
.
Решение:
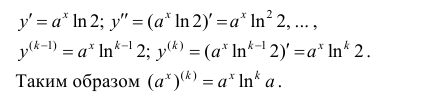
Пример:
Найти 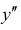 для функции y=y(x), заданной неявно:
для функции y=y(x), заданной неявно: 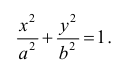
Решение:
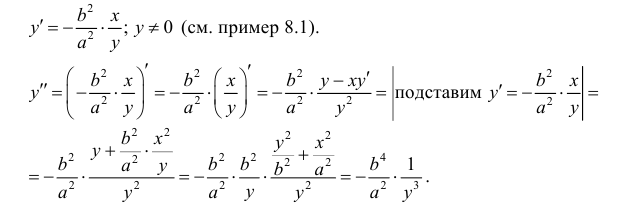
Пусть функция y=y(x) задана параметрически в виде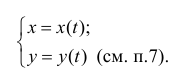
Пусть x(t) и y(t) дважды дифференцируемы и 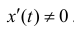 . Тогда (см. п. 7.2)
. Тогда (см. п. 7.2)
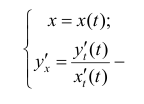 первая производная функции y=y(x).
первая производная функции y=y(x).
Рассуждая аналогично п. 7: 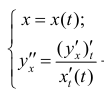 - вторая производная функции (10.1)
- вторая производная функции (10.1)
При этом 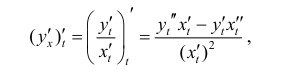 поэтому формула (10.1) перепишется в виде
поэтому формула (10.1) перепишется в виде
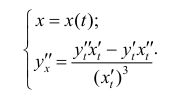
Пример:
Найти 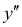 для функции y=y(x), заданной параметрически в виде
для функции y=y(x), заданной параметрически в виде 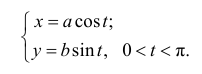
Решение:
По формуле (7.3)
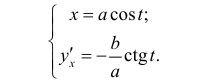
Далее, по формуле (10.1)
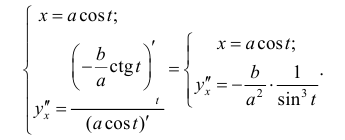
Теорема 10.1. Пусть Функции 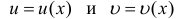 n раз дифференцируемы, тогда
n раз дифференцируемы, тогда
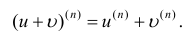 (10.2)
(10.2)
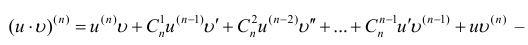 (10.3)
(10.3)
формула Лейбница, где 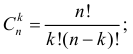 в частности:
в частности: 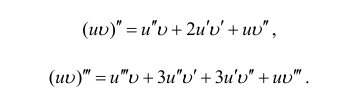
Пример:
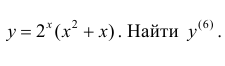
Решение:
По формуле (10.3):
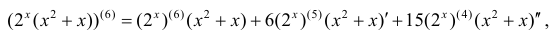
остальные слагаемые равны 0.
Далее 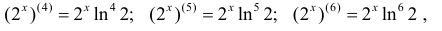 поэтому
поэтому
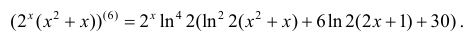
Определение 10.2. Пусть функция y=f(x) дифференцируема и 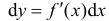 – ее дифференциал. Зафиксируем dx и будем рассматривать dy как функцию одной переменной х. Дифференциал от дифференциала dy функции y=f(x) будем называть вторым дифференциалом этой функции и обозначать
– ее дифференциал. Зафиксируем dx и будем рассматривать dy как функцию одной переменной х. Дифференциал от дифференциала dy функции y=f(x) будем называть вторым дифференциалом этой функции и обозначать 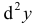 . Таким образом:
. Таким образом:
Аналогично 
Преобразуем формулы (10.4) и (10.5):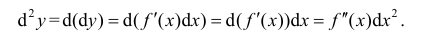
То есть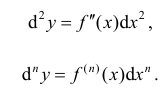
При вычислении 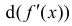 приращение независимой переменной берем
приращение независимой переменной берем
равным первоначальному приращению dx.
Пример:
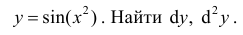 .
.
Решение:
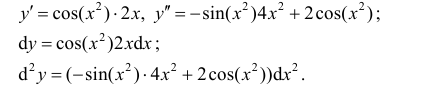
Свойство инвариантности верное для первого дифференциала не выполняется для второго.
Например, для функции 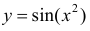 из примера 10.6 имеем
из примера 10.6 имеем 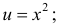
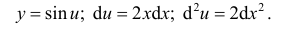
Тогда для первого дифференциала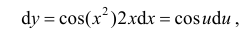 но
но
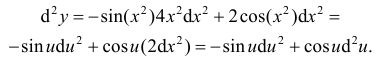
Таким образом 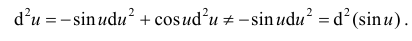
Если u=u(x), то для функции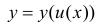 верна формула
верна формула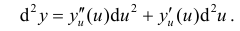
Если функции 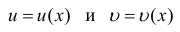 n раз дифференцируемы, то для
n раз дифференцируемы, то для 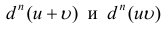 верны формулы, аналогичные формулам (10.2), (10.3).
верны формулы, аналогичные формулам (10.2), (10.3).
В частности:
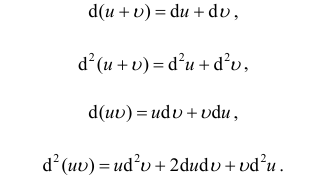
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |