
Производные тригонометрических функции с примерами решения
Производные тригонометрических функции
Рассмотрим производные тригонометрических функций. Правильны следующие формулы:
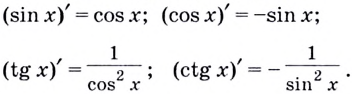
Для доказательства двух первых формул вспомним первый замечательный предел (см. с. 106), а именно: когда 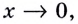
Теорема (о производной синуса). Для каждого действительного 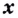
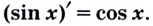
Доказательство. Найдём приращение функции 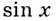 на промежутке
на промежутке 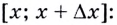
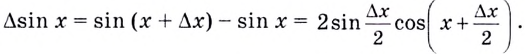
Поэтому
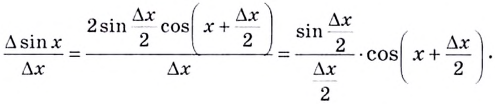
Если 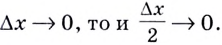 В этом случае
В этом случае 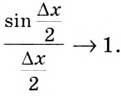 Известно также, что функция
Известно также, что функция 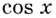 непрерывна на
непрерывна на 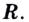 Поэтому если
Поэтому если 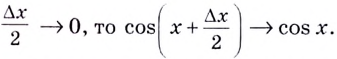
Следовательно, для произвольного 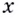
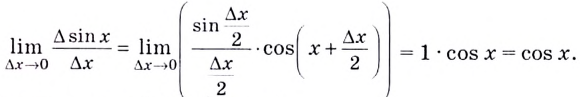
То есть, всегда 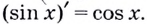
Теорема (о производной косинуса). Для каждого действительного 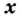
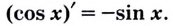
Доказательство.
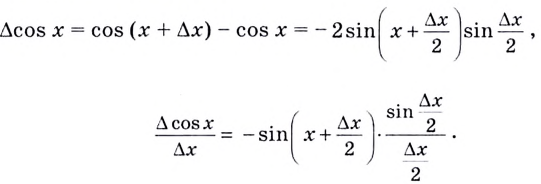
Если 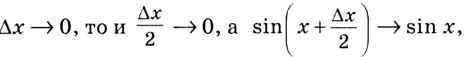 поскольку функция
поскольку функция 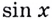 непрерывна на
непрерывна на 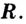 Следовательно, при каждом действительном
Следовательно, при каждом действительном 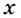
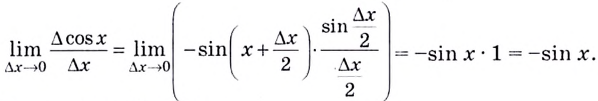
To есть 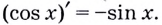
Формулы производных тангенса и котангенса можно доказать, используя теорему о производной частного:
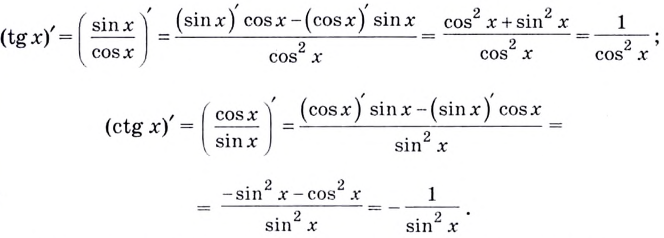
Итак, в каждой точке 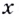 области определения функций:
области определения функций:
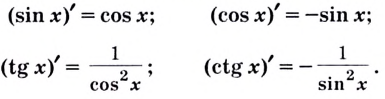
Пример №536
Найдите производную функции 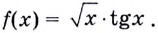
Решение:
Воспользуемся теоремой о производной произведения:
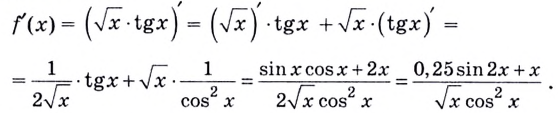
Пример №537
Вычислите значение производной функции 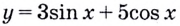 в точке
в точке 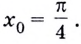
Решение:
Воспользуемся теоремой о производной суммы:
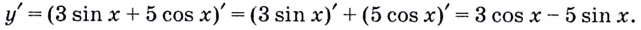
Если 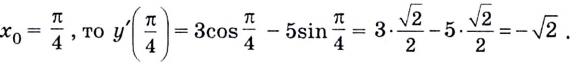
Ответ. 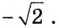
Пример №538
В какой точке касательная, проведённая к графику функции
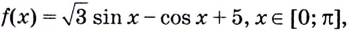 параллельна прямой
параллельна прямой 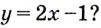
Решение:
В искомой точке угловой коэффициент 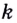 касательной равен 2, ибо параллельные прямые имеют равные угловые коэффициенты.
касательной равен 2, ибо параллельные прямые имеют равные угловые коэффициенты.
Кроме этого, угловой коэффициент 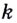 касательной, проведённой к графику функции
касательной, проведённой к графику функции 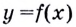 в точке
в точке 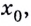 определяется формулой
определяется формулой 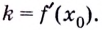 Можем составить уравнение
Можем составить уравнение 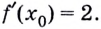
Найдём 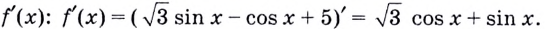
Абсциссу искомой точки найдём, решив уравнение 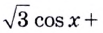
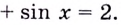
Имеем: 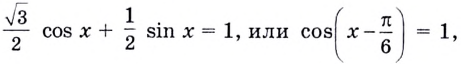 отсюда
отсюда 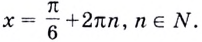
Промежутку 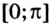 принадлежит только одна такая точка:
принадлежит только одна такая точка: 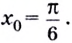
Тогда 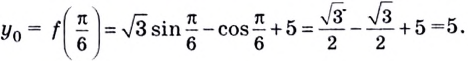
Ответ. 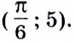
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |