
Производная сложной функции с примерами решения
Производная сложной функции
До сих пор рассматривались производные функций, аргументами которых была переменная 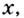
Рассматривая в функции 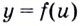 переменную
переменную 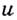 как аргумент, можно найти и производную этой функции по
как аргумент, можно найти и производную этой функции по 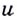 . Её мы будем обозначать знаком
. Её мы будем обозначать знаком 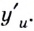 Производные функций по
Производные функций по 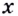 по-прежнему будем обозначать символами
по-прежнему будем обозначать символами 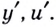
Теорема (о производной сложной функции). Пусть дана функция 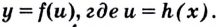 Если в какой-то точке
Если в какой-то точке 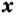 существует производная
существует производная 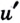 и в соответствующей точке
и в соответствующей точке 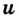 существует производная
существует производная 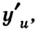 то существует также производная
то существует также производная 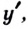 причём
причём 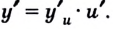
Строгое доказательство этой теоремы сложное, поэтому ограничимся только его схемой. Производная 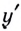 равна пределу отношения
равна пределу отношения 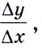 когда
когда 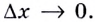 Считая, что
Считая, что 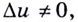 умножим числитель и знаменатель этого отношения на
умножим числитель и знаменатель этого отношения на 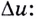
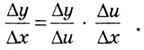
Если 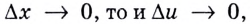 поскольку речь идет о функции
поскольку речь идет о функции 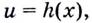 дифференцируемой в точке
дифференцируемой в точке 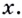 Поэтому если
Поэтому если 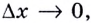 то
то
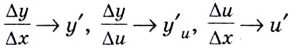
и из равенства 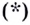 следует равенство
следует равенство 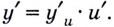
До сих пор речь шла о производной 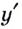 в некоторой фиксированной точке
в некоторой фиксированной точке 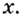 Если же данная сложная функция
Если же данная сложная функция 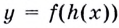 дифференцируема в каждой точке
дифференцируема в каждой точке 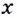 некоторого промежутка, то равенство
некоторого промежутка, то равенство 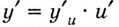 и выполняется на всём промежутке. Итак, пользуясь этим равенством, можно находить производную данной функции и как функцию, заданную на этом промежутке.
и выполняется на всём промежутке. Итак, пользуясь этим равенством, можно находить производную данной функции и как функцию, заданную на этом промежутке.
Пример:
Найдём производную функции 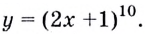 Это функция
Это функция 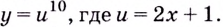 Эти функции дифференцируемы на
Эти функции дифференцируемы на 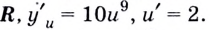
Итак, 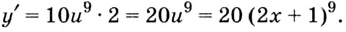
Не обязательно, решая такие упражнения, вводить переменную 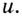 Её можно только представлять и сразу писать, например:
Её можно только представлять и сразу писать, например:
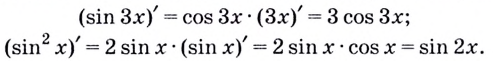
Производной данной функции 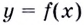 есть некоторая функция от того же аргумента
есть некоторая функция от того же аргумента 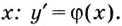 Её также можно дифференцировать: находить производную производной. В этом случае говорят о нахождении производной второго порядка. Производную от производной второго порядка называют производной третьего порядка.
Её также можно дифференцировать: находить производную производной. В этом случае говорят о нахождении производной второго порядка. Производную от производной второго порядка называют производной третьего порядка.
Для примера рассмотрим функцию 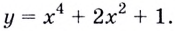 Найдём производную этой функции, производные образованных функций и запишем соответствующие названия:
Найдём производную этой функции, производные образованных функций и запишем соответствующие названия:
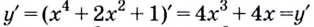 — производная первого порядка;
— производная первого порядка;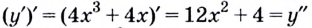 — производная второго порядка;
— производная второго порядка;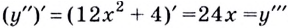 — производная третьего порядка;
— производная третьего порядка;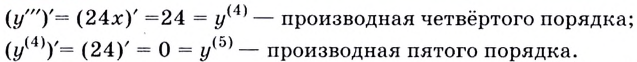
Понятно, что все производные следующих порядков 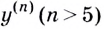 функции
функции 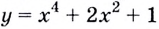 также равны нулю.
также равны нулю.
Производные второго и высших порядков используются для исследования функций различной природы.
Пример №539
Найдите 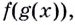 если:
если:

Решение:
а) По условию 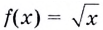 — внешняя функция, а
— внешняя функция, а 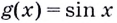 — внутренняя. Следовательно, аргументом внешней функции должна стать функция
— внутренняя. Следовательно, аргументом внешней функции должна стать функция 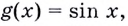 то есть вместо
то есть вместо 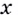 в выражении
в выражении 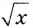 следует записать
следует записать 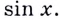 Имеем:
Имеем: 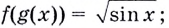
б) по условию 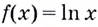 — внешняя функция, a g(x) = х2 + 1 — внутренняя. Следовательно, аргументом функции
— внешняя функция, a g(x) = х2 + 1 — внутренняя. Следовательно, аргументом функции 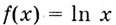 должна стать функция
должна стать функция 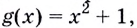 т. е. вместо
т. е. вместо 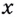 в выражении
в выражении 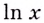 следует записать
следует записать 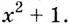 Имеем:
Имеем: 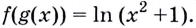
Пример №540
Выведите формулу для вычисления производной функции
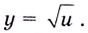
Решение:
Из данного равенства получаем 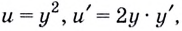 отсюда
отсюда 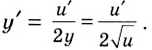
В частности, если 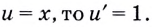 Следовательно,
Следовательно, 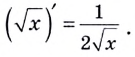
Пример №541
Найдите значение производной функции 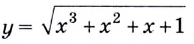 в точке
в точке 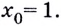
Решение:
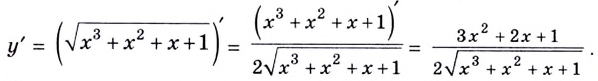
Если 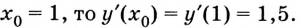
Пример №542
Найдите: 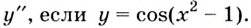
Решение:
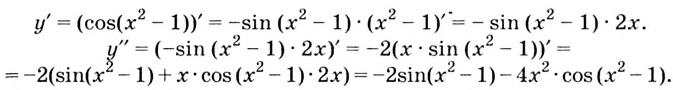
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |