Проецирование прямой в начертательной геометрии с примерами

Содержание:

Проецирование прямой:

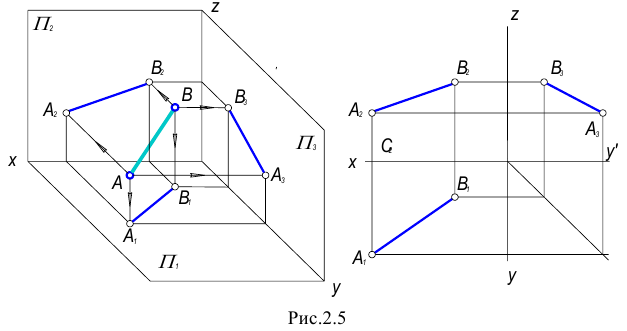
Аксиома евклидовой геометрии гласит: «Через две точки проходит единственная прямая». В связи с этим построение проекций прямой линии на КЧ сводится к построению двух точек ей принадлежащих (рис. 2.5.).

Точка пересечения прямой с плоскостью проекций называется следом прямой.

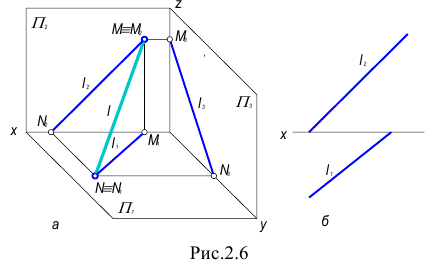
На рис. 2.6.а построены следы прямой  – горизонтальный след  и фронтальный 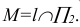Также на КЧ прямая может быть задана непосредственно своими проекциями (рис. 2.6 б).

Положение прямой относительно плоскостей проекций

По расположению прямых относительно плоскостей проекций различают прямые общего и частного положения. Прямые не параллельные и не перпендикулярные ни одной из плоскостей проекций называются прямыми общего положения. На КЧ ни одна из проекций прямой общего положения не  параллельна осям проекций (или не перпендикулярна линиям связи) (рис. 2.5, 2.6).

Прямые частного положения подразделяются на прямые уровня и проецирующие прямые.

Прямые, параллельные одной из плоскостей проекций называются прямыми уровня.

Существует три вида прямых уровня: горизонталь, фронталь и профильная прямая.

1. Горизонталь (h)– прямая, параллельная горизонтальной плоскости проекций (рис. 2.7).

Признаки и свойства горизонтали:

1. На КЧ фронтальная проекция горизонтали  располагается параллельно оси х (или в безосном чертеже перпендикулярно линиям связи).
2. На горизонтальную плоскость проекций проецируются без искажения отрезок принадлежащий горизонтали  и углы наклона ее к фронтальной 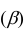 и профильной  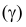плоскостям проекций.

2. Фронталь (f) – прямая, параллельная фронтальной плоскости проекций (рис.2.8)

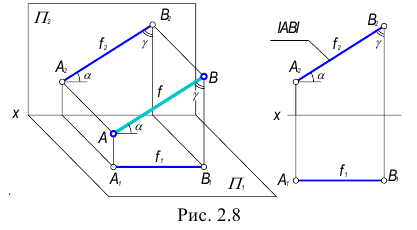
Признаки и свойства фронтали:

1. На КЧ горизонтальная проекция фронтали 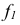 располагается параллельно оси х (или в безосном чертеже перпендикулярно линиям связи).
2. На фронтальную плоскость проекций проецируются без искажения отрезок принадлежащий фронтали 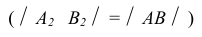 и углы наклона ее к горизонтальной  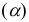и профильной  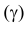плоскостям проекций.

3. Профильная прямая – прямая, параллельная профильной плоскости проекций.

Признаки и свойства профильной прямой:

1. На КЧ фронтальная 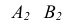 и горизонтальная  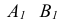проекция отрезка профильной прямой располагаются перпендикулярно оси х.
2. На профильную плоскость проекций проецируются без искажения отрезок принадлежащий профильной прямой 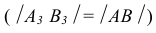 и углы наклона ее к фронтальной  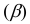и горизонтальной  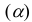плоскостям проекций.

Прямые, перпендикулярные одной из плоскостей проекций называются проецирующими прямыми.

Существует три вида проецирующих прямых: горизонтально- проецирующая, фронтально-проецирующая и профильно-проецирующие прямая. Проекцией проецирующей прямой на плоскость проекций к которой она перпендикулярна, является точка (след прямой).

1. Горизонтально-проецирующая прямая – прямая, перпендикулярная горизонтальной плоскости проекций.

• Заказать чертежи

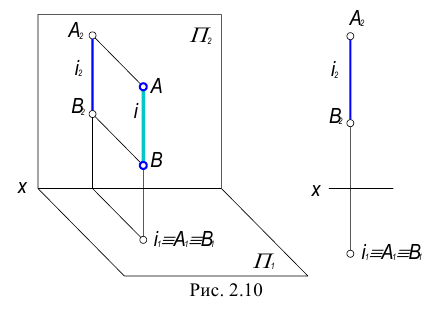
2. Фронтально-проецирующая прямая – прямая, перпендикулярная фронтальной плоскости проекций.

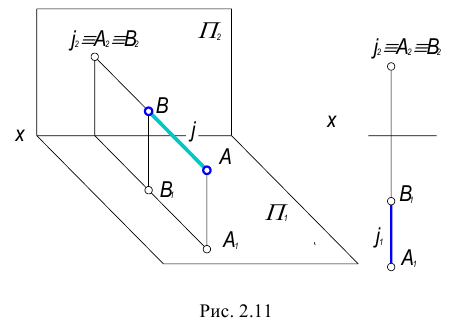
3. Профильно-проецирующая прямая – прямая, перпендикулярная профильной плоскости проекций.

Деление отрезка в заданном отношении

Теорема Фалеса: Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Используя эту теорему можно легко разделить любой отрезок в заданном отношении.

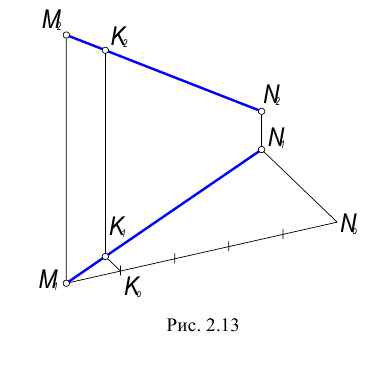
Натуральная величина отрезка прямой общего положения. Метод прямоугольного треугольника

В отличие от отрезков прямых частного положения, проецирующихся хотя бы на одну из плоскостей проекций в натуральную величину, отрезок прямой общего положения на плоскости проекций проецируется с искажением. Для того, чтобы найти его натуральную величину необходимо провести ряд преобразований. Существует несколько методов нахождения натуральной величины отрезка прямой общего положения и углов наклона его к плоскостям проекций. Одним из этих методов является метод прямоугольного треугольника, в котором находится зависимость длины проекции отрезка от его истинной величины.

Возьмем прямую общего положения АВ и спроецируем ее на горизонтальную плоскость проекций . Через точку А проведем линию, параллельную плоскости  Таким образом в пространстве получим прямоугольный треугольник  один из катетов которого (АВ’)  равен длине проекции отрезка, а угол, между отрезком и этим катетом является углом наклона заданного отрезка к плоскости проекций (рис. 2.14).

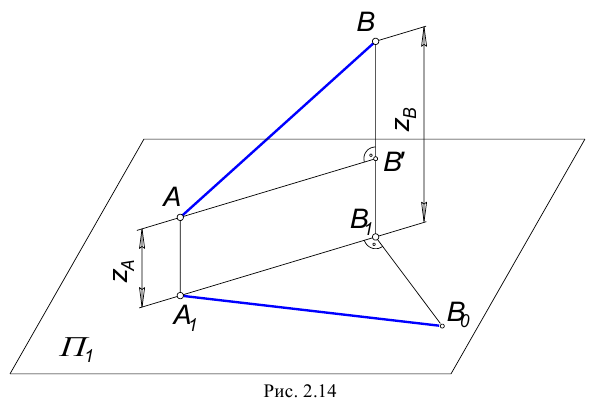
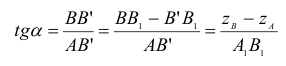
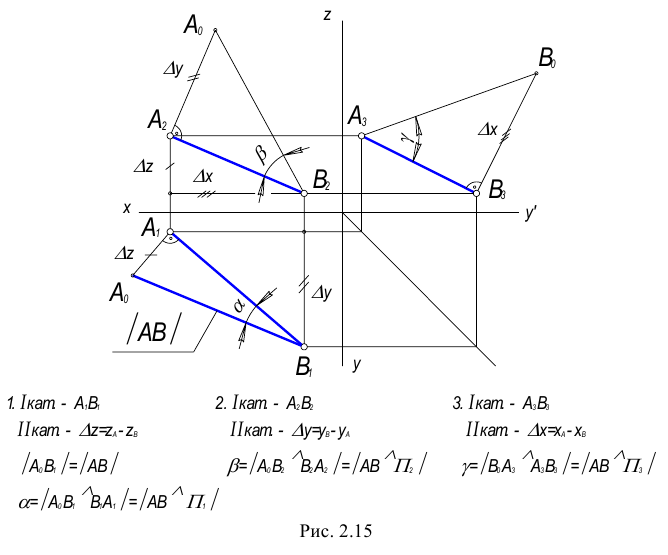
Для определения натуральной величины отрезка прямой общего положения и углов наклона ее к плоскости проекций на КЧ необходимо построить прямоугольный треугольник:

1. Первый катет этого треугольника равен проекции отрезка на плоскости проекций (обычно прямоугольный треугольник пристраивают к проекции отрезка, однако в некоторых задачах целесообразно прямоугольный треугольник строить в стороне от проекций геометрических объектов).
2. Из проекции любого конца отрезка (   или ) под прямым углом к проекции отрезка проводится луч, на котором откладывается длина второго катета, равная разности расстояний от концов отрезка до данной плоскости проекций.
3. Гипотенуза полученного таким образом прямоугольного треугольника равна длине заданного отрезка.
4. Угол наклона отрезка к той или иной плоскости проекций равен углу между гипотенузой - натуральной величиной и катетом – проекцией на эту плоскость проекций.

Следовательно, для определения угла наклона отрезка к горизонтальной плоскости проекций, прямоугольный треугольник строится на базе горизонтальной проекции отрезка, к фронтальной плоскости проекций – на базе фронтальной плоскости, к профильной плоскости проекций – на базе профильной проекции.