
Проецирование плоскости в начертательной геометрии с примерами
Содержание:
Положение плоскости в пространстве однозначно определяется положением трех ее точек. Следовательно, на эпюре плоскость может быть задана следующими способами:
- проекциями трех точек, не лежащих на одной прямой (рис.24);
- проекциями прямой и точки вне этой прямой (рис.25);
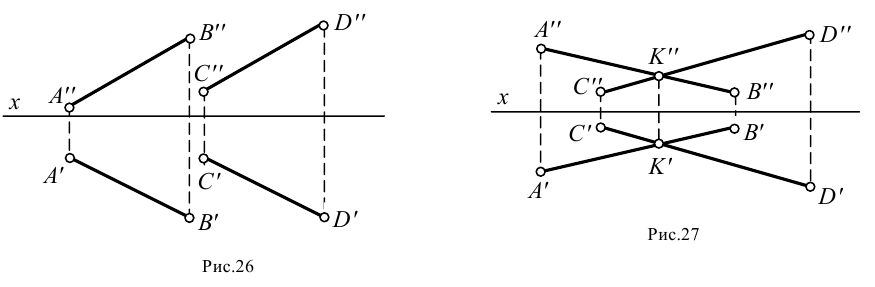
- проекциями двух параллельных прямых (рис.26);
- проекциями двух пересекающихся прямых (рис.27).
Каждое из представленных на рис.24-27 заданий плоскости может быть преобразовано одно в другое. Например, проведя через точки 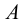
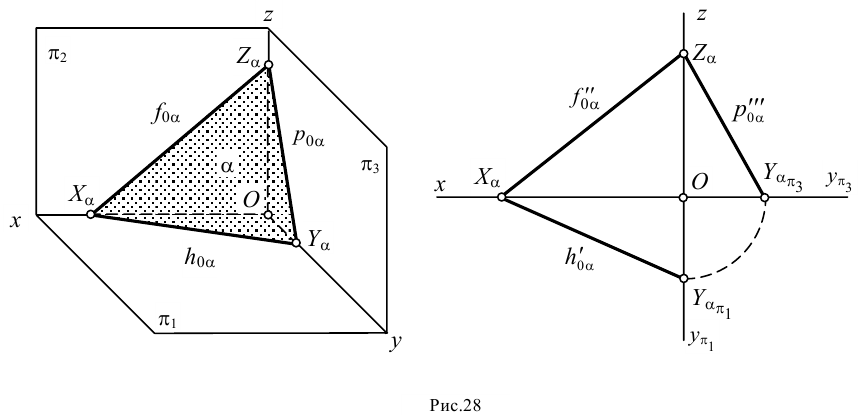
Помимо отмеченных случаев плоскость может быть задана на чертеже и проекциями любой плоской фигуры (треугольника, квадрата, круга и т.д.). Однако наиболее наглядным является изображение плоскости при помощи прямых, по которым она пересекает плоскости проекций (рис.28).
Прямые, по которым плоскость пересекается с плоскостями проекций, называют следами плоскости. В общем случае у плоскости будет три следа: горизонтальный 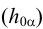 , фронтальный
, фронтальный 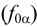 и профильный
и профильный 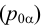 . Индекс «0» в обозначении плоскости означает, что этот след образован в пересечении с «нулевой» плоскостью, как раньше называли плоскости проекций.
. Индекс «0» в обозначении плоскости означает, что этот след образован в пересечении с «нулевой» плоскостью, как раньше называли плоскости проекций.
Точки на осях координат, в которых пересекаются следы плоскости - 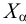 ,
, 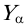 и
и 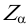 , называют точками схода следов. Три точки схода следов плоскости однозначно определяют положение плоскости в пространстве. Зная координаты точек схода следов (или длину отрезков
, называют точками схода следов. Три точки схода следов плоскости однозначно определяют положение плоскости в пространстве. Зная координаты точек схода следов (или длину отрезков 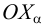 ,
, 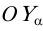 и
и 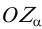 , которые иногда называют параметрами плоскости), можно однозначно задать положение плоскости.
, которые иногда называют параметрами плоскости), можно однозначно задать положение плоскости.
Следы плоскости сливаются со своими проекции на этой плоскости: 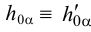 ,
, 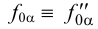 и
и 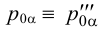 . Учитывая, что на эпюре мы изображаем только проекции геометрических элементов, следы плоскости мы задаем проекциями следов:
. Учитывая, что на эпюре мы изображаем только проекции геометрических элементов, следы плоскости мы задаем проекциями следов: 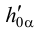 ,
, 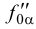 и
и 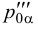 (рис.28). Каждый след плоскости проходит через две точки схода следов. Следовательно, любые два следа плоскости однозначно определяют ее положение в пространстве (исключение составляет осевая плоскость).
(рис.28). Каждый след плоскости проходит через две точки схода следов. Следовательно, любые два следа плоскости однозначно определяют ее положение в пространстве (исключение составляет осевая плоскость).
Плоскость, пересекающая все три плоскости проекций, называют плоскостью общего положения. Если плоскость перпендикулярна одной или двум плоскостям проекций, то ее называют плоскостью частного положения.
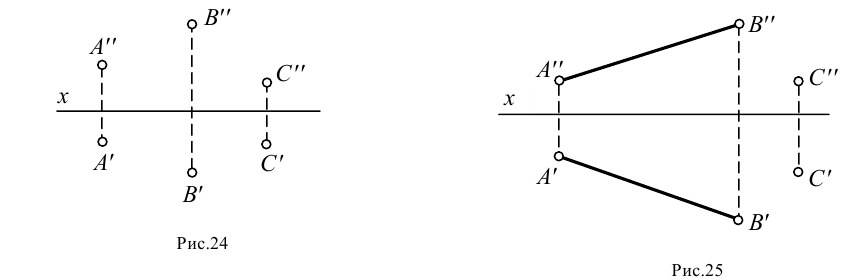
Плоскости, перпендикулярные одной плоскости проекций
Горизонтально-проецирующей называют плоскость, перпендикулярную плоскости 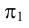 (рис.29). Фронтальный и профильный следы такой плоскости будут параллельны оси
(рис.29). Фронтальный и профильный следы такой плоскости будут параллельны оси 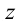 .
.
Фронтально-проецирующей называют плоскость, перпендикулярную плоскости 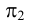 (рис.30). Горизонтальный и профильный следы фронтально-проецирующей плоскости будут параллельны оси
(рис.30). Горизонтальный и профильный следы фронтально-проецирующей плоскости будут параллельны оси 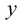 .
.
Фронтальная проекция любой точки, лежащей в этой плоскости (например, точки 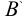 ), всегда расположена на фронтальном следе плоскости.
), всегда расположена на фронтальном следе плоскости.
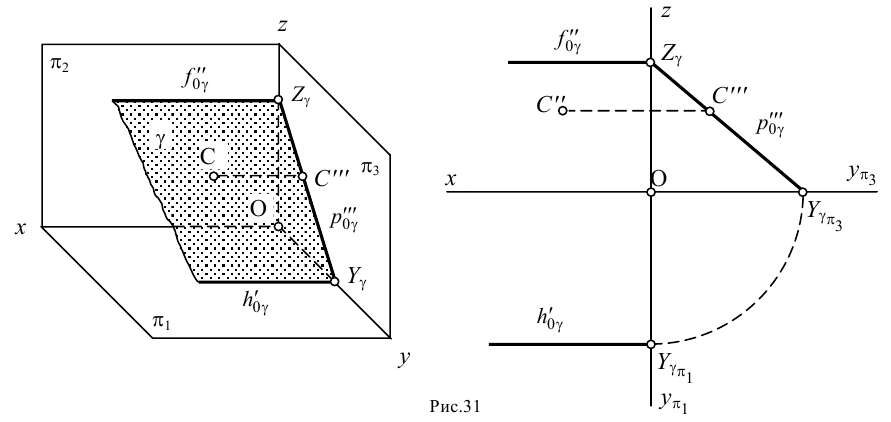
Профильно-проецирующей называют плоскость, перпендикулярную плоскости 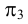 (рис.31). У такой плоскости фронтальный и горизонтальный следы будут параллельны оси
(рис.31). У такой плоскости фронтальный и горизонтальный следы будут параллельны оси 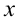 .
.
Профильная проекция любой точки, лежащей в этой плоскости (например, точки 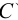 ), всегда расположена на профильном следе плоскости.
), всегда расположена на профильном следе плоскости.
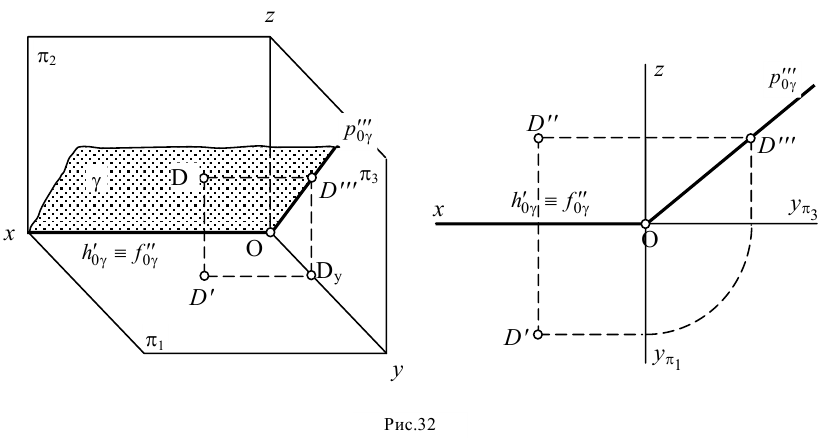
Осевой называют плоскость, проходящую через ось проекций. Осевая плоскость будет всегда перпендикулярна одной из плоскостей проекций, поэтому ее можно рассматривать как частный случай горизонтально-, фронтально- или профильно-проецирующей плоскости. У осевой плоскости два следа совпадают с одной из осей проекций (на рис.32 - с осью 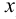 ).
).
Для однозначного определения положения осевой плоскости необходимо знать положение всех трех ее следов или двух сливающихся следов и еще хотя бы одной точки, лежащей в этой плоскости.
Плоскости, перпендикулярные двум плоскостям проекций
Если плоскость перпендикулярна двум плоскостям проекций, то она параллельна третьей плоскости проекций. Для таких плоскостей встречается общее название - плоскости уровня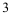 .
.
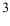 Ряд авторов считает, что это название относится только к горизонтальной плоскости.
Ряд авторов считает, что это название относится только к горизонтальной плоскости.
Плоскость, параллельная плоскости 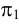 называется горизонтальной плоскостью (рис.33). На эпюре ее фронтальный и профильный следы сливаются в одну линию, перпендикулярную оси
называется горизонтальной плоскостью (рис.33). На эпюре ее фронтальный и профильный следы сливаются в одну линию, перпендикулярную оси 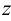 . Фронтальные и профильные проекции точек, лежащих в горизонтальной плоскости (например, точки
. Фронтальные и профильные проекции точек, лежащих в горизонтальной плоскости (например, точки 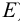 ), располагаются соответственно на фронтальном и профильном следах плоскости. Любой геометрический объект, лежащий в горизонтальной плоскости, проецируется на плоскость
), располагаются соответственно на фронтальном и профильном следах плоскости. Любой геометрический объект, лежащий в горизонтальной плоскости, проецируется на плоскость 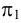 в натуральную величину.
в натуральную величину.
Аналогичным образом можно построить фронтальную и профильную плоскости, т.е. плоскости, параллельные соответственно фронтальной и профильной плоскостям проекций.
Отмеченные особенности проецирования плоскостей частного положения в дальнейшем изложении курса будут использованы для упрощения решения ряда метрических и позиционных задач.
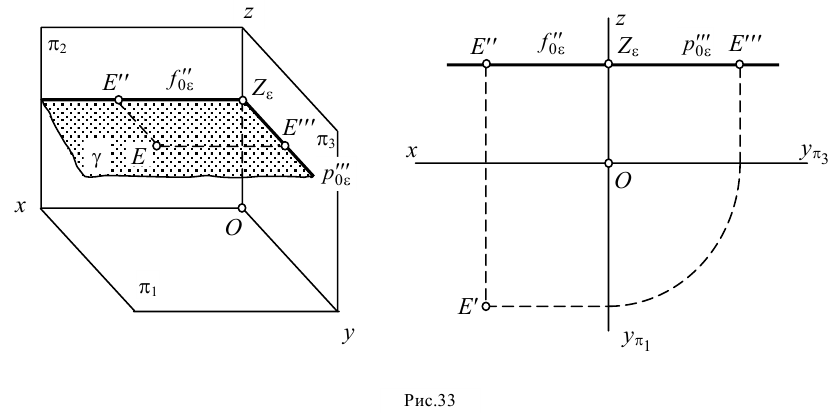
Взаимное положение прямой и плоскости
Прямая может занимать относительно плоскости следующие положения:
- лежать в плоскости;
- быть параллельной плоскости;
- пересекать плоскость (частный случай пересечения - прямая может быть перпендикулярна плоскости).
Прямая лежит в плоскости, если проходит через две точки, принадлежащие этой плоскости.
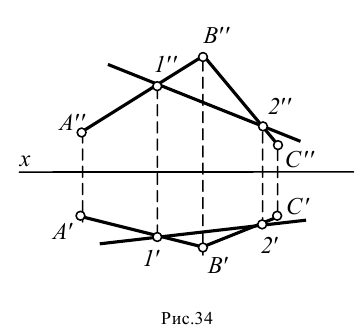
Пусть плоскость задана двумя пересекающимися прямыми 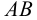 и
и 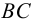 . Проводим в этой плоскости произвольную прямую
. Проводим в этой плоскости произвольную прямую 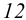 . Для этого выбираем некоторую точку
. Для этого выбираем некоторую точку 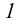 на прямой
на прямой 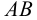
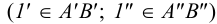 и точку
и точку 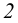 на прямой
на прямой  и проводим прямую
и проводим прямую 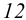 с проекциями
с проекциями 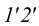 и
и 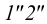 (рис.34). Эта прямая лежит в заданной плоскости, так как проходит через две точки (точки
(рис.34). Эта прямая лежит в заданной плоскости, так как проходит через две точки (точки 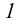 и
и 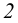 ), лежащие в заданной плоскости.
), лежащие в заданной плоскости.
Рассмотрим вариант, когда плоскость задана следами: прямая лежит в плоскости, если следы прямой лежат на одноименных следах плоскости (рис.35). Это же правило можно сформулировать и иначе: плоскость проходит через прямую, если ее следы проходят через одноименные следы прямой.
Если некоторая плоскость задана двумя пересекающимися прямыми, то для построения следов такой плоскости достаточно найти следы этих прямых и одноименные следы соединить прямыми линиями - эти прямые и будут искомыми следами плоскости. Аналогично могут быть построены следы плоскости, заданной двумя параллельными прямыми.
Поскольку случаи задания плоскости тремя точками, не лежащими на одной прямой, и прямой и точкой вне этой прямой всегда могут быть сведены к случаю задания плоскости двумя прямыми, то можно сказать, что для построения следов плоскости, заданной любым известным способом, необходимо построить следы двух любых прямых этой плоскости и через одноименные следы прямых провести искомые следы плоскости.
Пример 5. Построить три следа плоскости 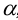 , заданной двумя пересекающимися прямыми
, заданной двумя пересекающимися прямыми  и
и 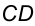 (рис.36).
(рис.36).
1. Строим проекции горизонтальных следов прямых 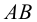 и
и 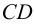 (рис.37):
(рис.37):  . Фронтальные проекции горизонтальных следов лежат на пересечении фронтальных проекций прямых с осью
. Фронтальные проекции горизонтальных следов лежат на пересечении фронтальных проекций прямых с осью 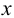 :
:
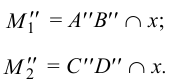
Горизонтальные проекции горизонтальных следов лежат на пересечении линий проекционной связи, проведенных из точек 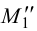 и
и 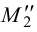 , с соответствующей горизонтальной проекцией прямой:
, с соответствующей горизонтальной проекцией прямой:
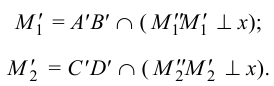
2. Строим проекции фронтальных следов прямых 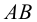 и
и 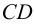 :
: 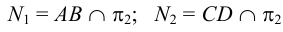 . Горизонтальные проекции фронтальных следов лежат в точке пересечения горизонтальных проекций прямых с осью
. Горизонтальные проекции фронтальных следов лежат в точке пересечения горизонтальных проекций прямых с осью 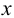 :
:
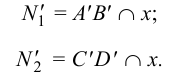
Фронтальные проекции фронтальных следов лежат на пересечении фронтальных проекций прямых с линиями проекционной связи, проведенными из точек 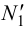 и
и 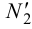 :
:
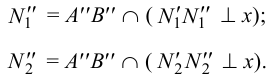
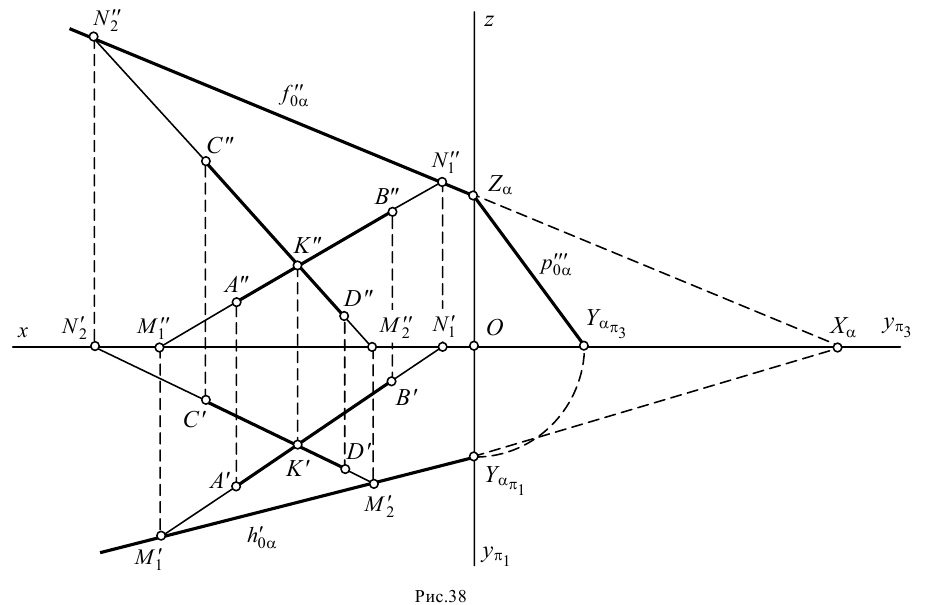
3. Через одноименные проекции следов проводим соответствующие следы плоскости (рис.38). Горизонтальный след плоскости 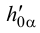 проводим через горизонтальные проекции горизонтальных следов
проводим через горизонтальные проекции горизонтальных следов 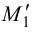 и
и 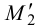 . Фронтальный след
. Фронтальный след 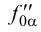 проводим через фронтальные проекции фронтальных следов
проводим через фронтальные проекции фронтальных следов 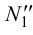 и
и 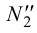 .
.
4. В пересечении горизонтального 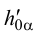 и фронтального следов
и фронтального следов 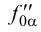 с осью
с осью 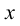 отмечаем точку схода следов
отмечаем точку схода следов 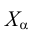 и проверяем правильность построений:
и проверяем правильность построений: 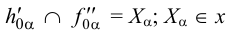 .
.
5. В пересечении горизонтального 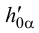 и фронтального
и фронтального 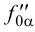 следов с осями проекций
следов с осями проекций 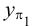 и
и 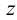 отмечаем точки схода следов соответственно
отмечаем точки схода следов соответственно 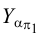 и
и 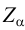 .
.
6. Точку схода следов 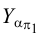 с оси
с оси 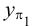 переносим на соответствующее по знаку направление оси
переносим на соответствующее по знаку направление оси 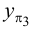 , где отмечаем точку
, где отмечаем точку 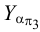 . Через точки схода следов
. Через точки схода следов 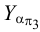 и
и 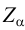 строим профильный след
строим профильный след 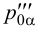 .
.
Прямые частного положения в плоскости
В каждой плоскости можно провести бесчисленное множество прямых линий частного положения. Рассмотрим некоторые прямые, лежащие в плоскости и занимающие относительно плоскостей проекций частные положения.
Горизонталь плоскости — это прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций 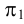 . Она обладает всеми свойствами горизонтальной прямой: ее фронтальная проекция параллельна оси
. Она обладает всеми свойствами горизонтальной прямой: ее фронтальная проекция параллельна оси 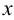 , а на горизонтальную плоскость проекций она проецируется в истинную величину.
, а на горизонтальную плоскость проекций она проецируется в истинную величину.
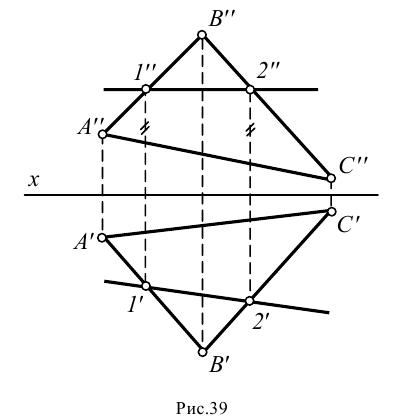
Построим любую горизонталь плоскости, заданной треугольником 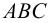 (рис.39). Фронтальную проекцию горизонтали
(рис.39). Фронтальную проекцию горизонтали 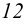 получаем, построив
получаем, построив 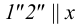 (расстояние от оси
(расстояние от оси 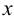 выберем произвольно). Строим горизонтальные проекции точек
выберем произвольно). Строим горизонтальные проекции точек 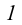 и
и 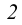
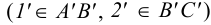 , и через
, и через 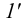 и
и 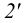 проводим горизонтальную проекцию горизонтали.
проводим горизонтальную проекцию горизонтали.
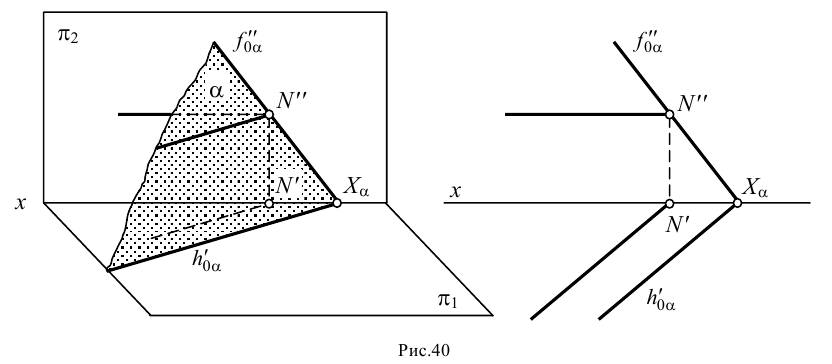
Если плоскость задана следами (рис.40), то горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.
Следует отметить одну интересную особенность горизонтальных проекций горизонталей плоскости: все они параллельны между собой и, поскольку они параллельны горизонтальному следу этой плоскости, положение любой из них определяет направление горизонтального следа плоскости.
Фронталь плоскости - это прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций. Горизонтальная проекция фронтали параллельна оси 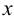 , а фронтальная проекция - ее истинная величина.
, а фронтальная проекция - ее истинная величина.
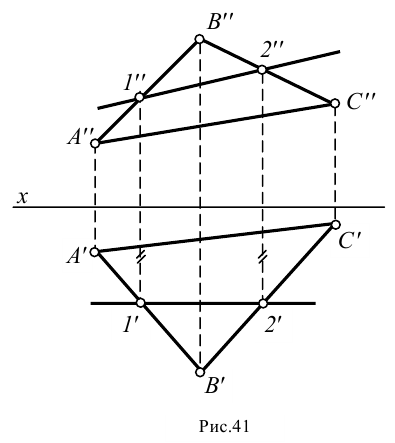
Пример построения фронтали плоскости, заданной треугольником 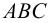 , дан на рис.41 (построение выполнено аналогично построению горизонтали на рис.39).
, дан на рис.41 (построение выполнено аналогично построению горизонтали на рис.39).
В плоскости, заданной следами, фронтальная проекция фронтали параллельна фронтальному следу плоскости (рис.42).
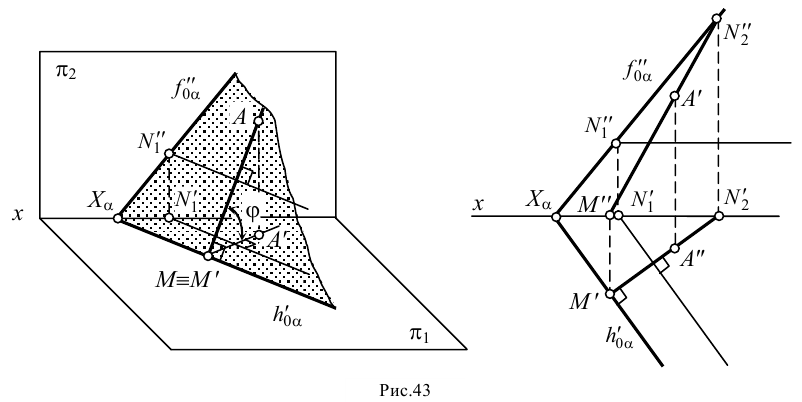
Линия наибольшего ската - это прямая, лежащая в плоскости и перпендикулярная горизонталям этой плоскости. На рис.43 построена прямая 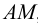 , являющаяся линией наибольшего ската плоскости
, являющаяся линией наибольшего ската плоскости 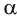 . Прямой угол между линией наибольшего ската плоскости и любой горизонталью этой плоскости проецируется на плоскость
. Прямой угол между линией наибольшего ската плоскости и любой горизонталью этой плоскости проецируется на плоскость 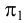 без искажения (на основании правил проецирования плоских углов). Следовательно, горизонтальная проекция линии наибольшего ската перпендикулярна горизонтальной проекции любой горизонтали или горизонтальному следу плоскости.
без искажения (на основании правил проецирования плоских углов). Следовательно, горизонтальная проекция линии наибольшего ската перпендикулярна горизонтальной проекции любой горизонтали или горизонтальному следу плоскости.
Из всех прямых, принадлежащих плоскости, линия наибольшего ската имеет самый большой угол наклона 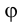 к горизонтальной плоскости проекций, который называется углом падения данной плоскости. В горно-геологической практике угол падения -это одна из важнейших характеристик изображаемого объекта (земной поверхности, пласта полезного ископаемого и т.п.).
к горизонтальной плоскости проекций, который называется углом падения данной плоскости. В горно-геологической практике угол падения -это одна из важнейших характеристик изображаемого объекта (земной поверхности, пласта полезного ископаемого и т.п.).
Пример 6. Через точку 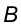 построить линию наибольшего ската плоскости, заданной треугольником
построить линию наибольшего ската плоскости, заданной треугольником 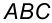 (рис.44).
(рис.44).
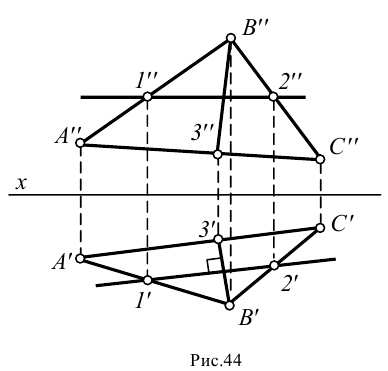
1. Строим произвольную горизонталь 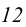 плоскости треугольника
плоскости треугольника 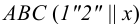 .
.
2. Прямая 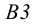 является линией наибольшего ската плоскости треугольника
является линией наибольшего ската плоскости треугольника 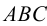 , так как
, так как 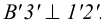 .
.
Рассмотренные нами прямые частного положения, лежащие в плоскости, главным образом горизонтали и фронтали, весьма часто применяют в различных построениях в качестве вспомогательных прямых.
Прямая, параллельная плоскости
Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости. Построим через точку 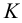 прямую, параллельную плоскости треугольника
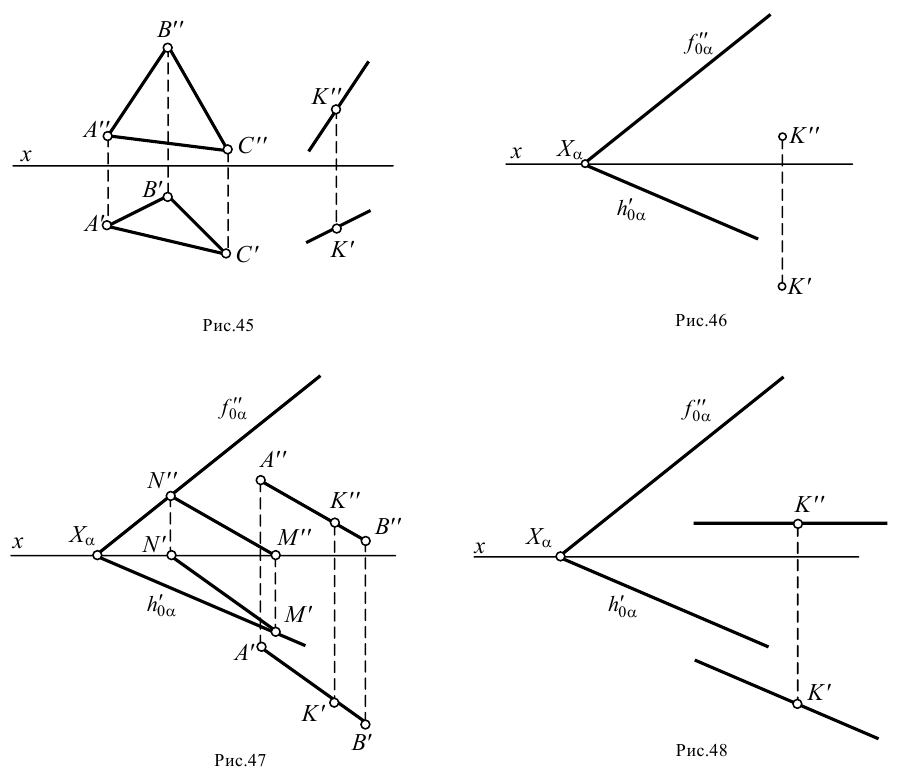
прямую, параллельную плоскости треугольника 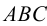 (рис.45). Сразу отметим, что задача имеет бесчисленное множество решений, так как через данную точку можно провести неограниченное количество прямых, параллельных данной плоскости. Через точку
(рис.45). Сразу отметим, что задача имеет бесчисленное множество решений, так как через данную точку можно провести неограниченное количество прямых, параллельных данной плоскости. Через точку 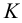 проведена прямая, параллельная стороне треугольника
проведена прямая, параллельная стороне треугольника 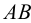 . Горизонтальная проекция этой прямой параллельна
. Горизонтальная проекция этой прямой параллельна 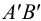 , а фронтальная -
, а фронтальная - 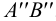 . Эта прямая параллельна плоскости треугольника
. Эта прямая параллельна плоскости треугольника 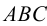 , так как она параллельна прямой, лежащей в плоскости треугольника
, так как она параллельна прямой, лежащей в плоскости треугольника 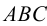 .
.
Пример 7. Через точку 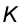 провести прямую, параллельную плоскости
провести прямую, параллельную плоскости 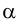 (рис.46).
(рис.46).
1. Проведем в плоскости 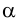 любую прямую, например прямую
любую прямую, например прямую 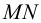 (рис.47). Затем через точку
(рис.47). Затем через точку 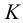 параллельно
параллельно 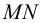 проведем прямую
проведем прямую 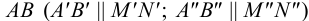 . Эта прямая будет параллельна плоскости
. Эта прямая будет параллельна плоскости 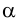 , так как она параллельна прямой
, так как она параллельна прямой 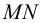 , лежащей в этой плоскости.
, лежащей в этой плоскости.
2. Эту же задачу, можно решить другим способом, проведя через точку 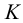 прямую частного положения, например, горизонтальную прямую (рис.48). Горизонтальная проекция горизонтальной прямой проходит через проекцию
прямую частного положения, например, горизонтальную прямую (рис.48). Горизонтальная проекция горизонтальной прямой проходит через проекцию 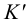 и параллельна следу
и параллельна следу 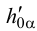 , а ее фронтальная проекция проходит через
, а ее фронтальная проекция проходит через 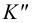 параллельно оси
параллельно оси 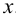 .
.
Точка в плоскости
Точка лежит в плоскости, если она лежит на прямой, принадлежащей этой плоскости. Для того, чтобы в некоторой плоскости построить произвольную точку, зачастую необходимо предварительно построить некоторую прямую, принадлежащую заданной плоскости, а на прямой - точку.
Пример 8. Построить недостающую проекцию точки 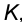 , лежащей в заданной плоскости (плоскость задана двумя пересекающимися прямыми
, лежащей в заданной плоскости (плоскость задана двумя пересекающимися прямыми  и
и 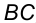 , а точка - только ее фронтальной проекцией
, а точка - только ее фронтальной проекцией 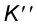 (рис.49).
(рис.49).
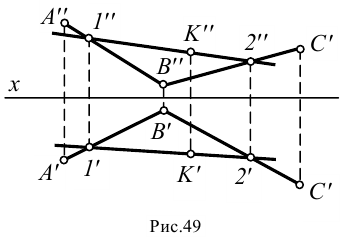
- Через точку
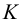 проводим произвольную прямую
проводим произвольную прямую 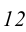 , принадлежащую заданной плоскости:
, принадлежащую заданной плоскости: 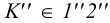 .
. - Строим горизонтальные проекции точек
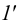 и
и 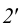 :
: 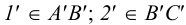 .
. - Через
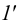 и
и 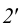 проводим горизонтальную проекцию прямой
проводим горизонтальную проекцию прямой 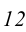 .
. - В пересечении линии проекционной связи, проведенной из
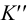 , и линии
, и линии 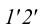 находим горизонтальную проекцию точки
находим горизонтальную проекцию точки 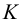 .
.
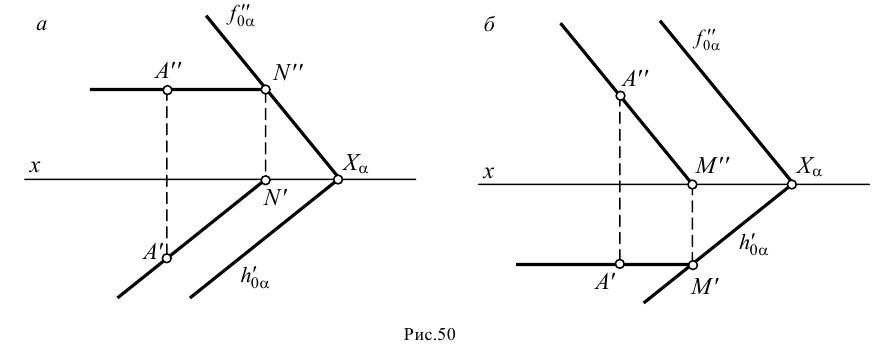
Если плоскость задана следами, то недостающая проекция точки, принадлежащей заданной плоскости, может быть найдена при помощи горизонтали (рис.50, а) или фронтали (рис.50, б) плоскости.
Пример 9. По заданной фронтальной проекции треугольника 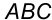 , принадлежащей плоскости
, принадлежащей плоскости 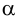 , построить его горизонтальную проекцию (рис.51).
, построить его горизонтальную проекцию (рис.51).
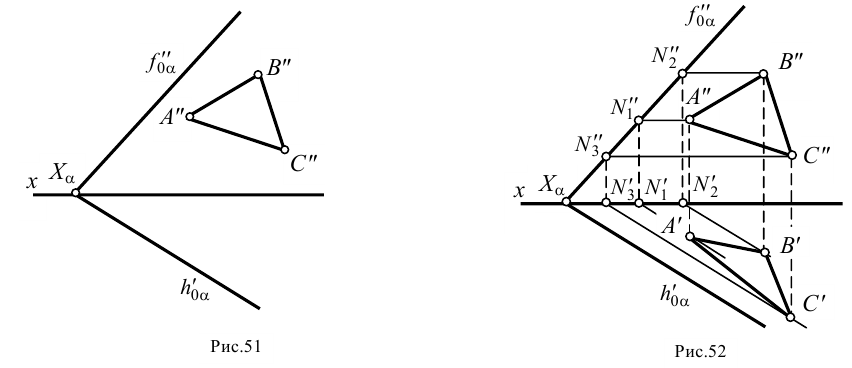
- Через точки
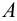 ,
, 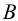 и
и 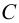 проводим в плоскости
проводим в плоскости 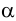 прямые частного положения, например горизонтали плоскости
прямые частного положения, например горизонтали плоскости 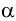 (рис.52). Фронтальные проекции этих прямых проводим через точки
(рис.52). Фронтальные проекции этих прямых проводим через точки 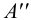 ,
, 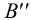 ,
, 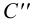 параллельно оси
параллельно оси 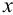 . Отмечаем проекции фронтальных следов горизонталей (фронтальные проекции - точки
. Отмечаем проекции фронтальных следов горизонталей (фронтальные проекции - точки 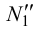 ,
, 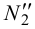 ,
, 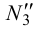 - лежат на следе
- лежат на следе 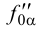 , а горизонтальные проекции -точки
, а горизонтальные проекции -точки 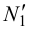 ,
, 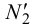 ,
,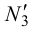 - на оси
- на оси 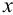 ). Проводим горизонтальные проекции горизонталей параллельно следу
). Проводим горизонтальные проекции горизонталей параллельно следу 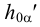 через точки соответственно
через точки соответственно 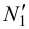 ,
, 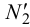 ,
, 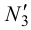 .
. - Находим горизонтальные проекции точек
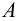 ,
, 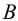 ,
, 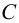 - точки
- точки 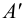 ,
, 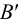 ,
, 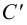 - в пересечении линий проекционной связи, проведенных из
- в пересечении линий проекционной связи, проведенных из 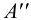 ,
, 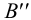 и
и 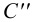 , с соответствующей горизонтальной проекцией горизонтали плоскости. Соединив
, с соответствующей горизонтальной проекцией горизонтали плоскости. Соединив 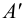 ,
, 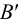 ,
, 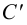 , получим горизонтальную проекцию треугольника
, получим горизонтальную проекцию треугольника  .
.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |