Проекции с числовыми отметками в начертательной геометрии с примерами

Содержание:

Метод проекций с числовыми отметками получил широкое применение в инженерно-строительном деле для изображения и проектирования на земной поверхности различных инженерных сооружений (железные и шоссейные дороги, котлованы, каналы, плотины, строительные площадки), а также для изображения земной поверхности. Этот метод применяется в том случае, когда размеры проектируемых объектов по длине значительно превышают размеры по высоте.

Проекции с числовыми отметками представляют собой прямоугольные проекции точек на горизонтальной плоскости, сопровождающиеся числами, указывающими удаление самих точек от этой плоскости.

Горизонтальная плоскость 

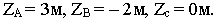
Положение горизонтальных проекций точек 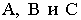 определяется координатами  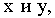а фронтальные проекции заменяют их числовые отметки, которые указывают удаление (обычно в  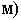точек от плоскости нулевого уровня. Точки, расположенные над плоскостью  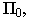имеют положительные отметки, расположенные под плоскостью  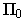- отрицательные. Точка, лежащая в плоскости  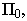имеет нулевую отметку.

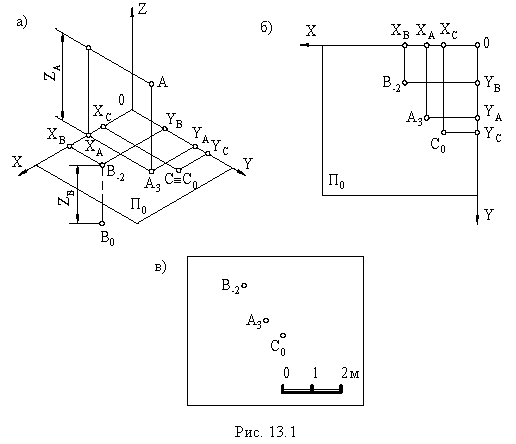
Изображение в проекциях с числовыми отметками, показанное на рис. 13.1, в, обычно называется планом. На планах необходимо вычерчивать линейный масштаб, который используется при решении различных метрических задач.

Прямая

В проекциях с числовыми отметками прямую общего положения можно задавать прямоугольными проекциями двух точек на плоскости нулевого уровня .указав их отметки ( рис.13.2, а и б) 

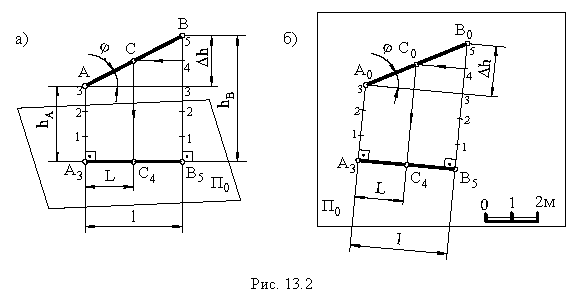
Длина горизонтальной проекции отрезка прямой называется заложением прямой (1).

Точки 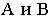 подняты относительно плоскости  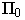на высоту, равную  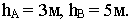Составив отношение разности высот концов отрезка  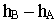к заложению  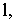получим величину, которая называется уклоном прямой:

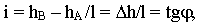
где 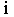 - уклон прямой  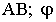- угол наклона прямой  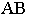к плоскости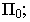 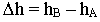 - превышение прямой  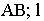- заложение прямой.

Заложение прямой, соответствующее единице превышения называют интервалом прямой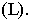 

Если 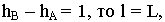 отсюда следует, что уклон и интервал прямой являются величинами обратными, т.е.

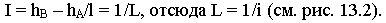
Градуированием прямой называется нахождение на горизонтальной проекции прямой точек с целыми числовыми отметками, разность между которыми равна единице (см. рис. 13.2).

Градуирование прямой можно выполнять разными способами. Один из способов показан на рис. 13.2, б. В этом случае необходимо восстановить перпендикуляры к проекции отрезка в точках 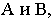 ограничивающих прямую, и отложить на них отрезки, равные высотам этих точек. При этом длина отрезка  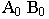является натуральной величиной. На рис 13.2, б из точек  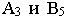восстановлены перпендикуляры и на них отложены отрезки, равные 3 и 5 единицам линейного масштаба. Через полученные точки с помощью вспомогательных прямых, параллельных горизонтальной проекции отрезка, найдены на прямой  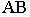точки с целыми отметками, которые затем спроецированы перпендикулярно на проекцию прямой. Расстояние  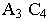является интервалом прямой. Другим способом градуирования является пропорциональное деление отрезка. На рис. 13.3 приведен этот способ.

Пропорциональное деление отрезка заключается в делении его горизонтальной проекции на 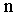 равных частей, где  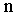- разность числовых отметок двух точек, задающих этот отрезок (в данном случае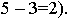 

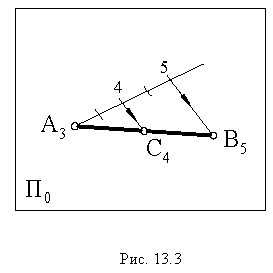
Для нахождения на прямой отметок с целыми числами необходимо провести через точку 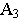 вспомогательную прямую под любым углом к проекции отрезка и на ней отложить два равных отрезка произвольной длины. Проведя отрезки  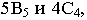получаем на отрезке  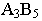точку, которая имеет целую отметку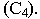 

Взаимное положение двух прямых линии

Две прямые в пространстве могут быть взаимно параллельны, могут пересекаться или скрещиваться друг с другом.

Параллельные прямые

В этом случае их проекции параллельны друг другу, интервалы равны и отметки возрастают в одном направлении (рис. 13.4).

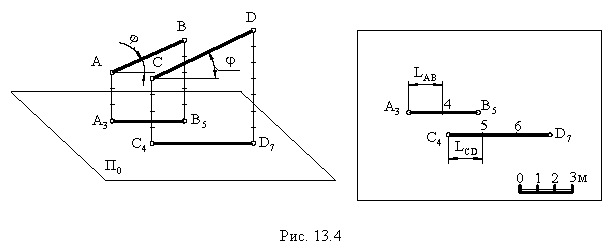
Пересекающиеся прямые

Проекции пересекающихся прямых пересекаются, и в точке пересечения проекций прямые имеют одинаковую отметку.

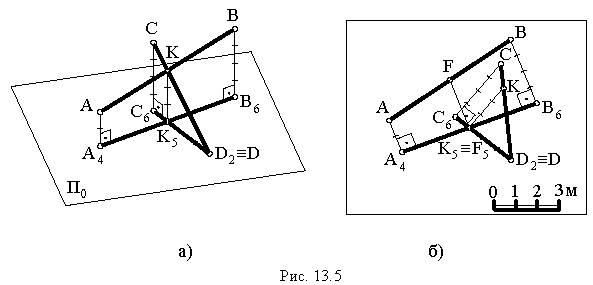
На рис. 13.5, а изображены прямые, горизонтальные проекции которых пересекаются Чтобы определить, пересекаются ли эти прямые в пространстве, необходимо найти отметки точек пересечения прямых в пересечении их проекций.

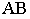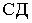На рис 13.5, б для определения взаимного положения прямых  и  в пространстве выполняем следующие построения:

1. градуируем прямые 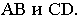 Для этого восстанавливаем перпендикуляры из точек  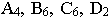к соответствующим проекциям прямых и откладываем на перпендикулярах отрезки, равные высотам точек;
2. получив натуральные величины прямых 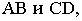 определяем отметки точек пересечения прямых в пересечении их проекций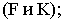 
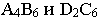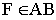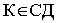3. прямые  пересекаются, так как отметки точек  и  равны 

Скрещивающиеся прямые

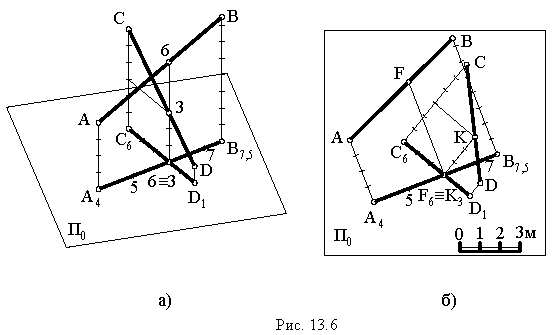
Проекции скрещивающихся прямых пересекаются, и в точке пересечения их проекций прямые имеют разные числовые отметки. На рис. 13.6, а показаны проекции скрещивающихся прямых, которые пересекаются. Числовые отметки в точке пересечения проекций определяем так же, как в предыдущей задаче. На рис. 13.6, б видно, что в точке пересечения проекций прямые имеют неодинаковые отметки