Проекции с числовыми отметкам в начертательной геометрии с примерами

Содержание:

Область применении и сущность способа проецирования:

Архитектор, проектируя здания и сооружения, всегда учитывает условия их расположения на отдельном участке местности. Нередко эти условия в определенной степени влияют на композиционные решения. Кроме чертежей, относящихся к зданию - планов, разрезов, фасадов и др. - проект должен включать все соображения по организации участка связи здания с рельефом местности. Эта часть проекта называется проектом вертикальной планировки. При разработке проекта вертикальной планировки требуется знания особого метода изображения объектов (рельефа), который получил название проекции с числовыми отметками.

Сущность этого метода заключается в том, что объект (рельеф) ортогонально проецируется на одну горизонтальную плоскость. У проекций точек и линий ставятся числа, показывающие расстояния этих точек и линий от условно принятой плоскости проекции, которая называется нулевой. Эти числа и называются числовыми отметками.

Проекции точек

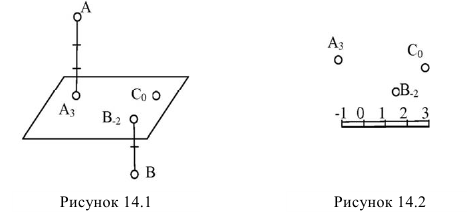
На рисунке 14.1 изображена горизонтальная основная плоскость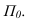

Точка А находится над плоскостью на высоте четырех единиц масштаба.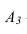

Точка С лежит на плоскости 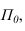поэтому ее проекция - С0.

Точка В находится под плоскостью, поэтому ее проекция - 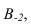, где отметка 2 со знаком (-).

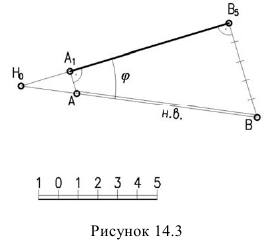
Для перехода к плоскому чертежу, плоскость По совмещается с плоскостью чертежа, граница плоскости не указывается. На чертеже обязательно указывается масштаб. Числовая отметка каждой точки, по сути, заменяет фронтальную проекцию, т.е. соответствует координате Z (рисунок 14.2).

Проекции прямых. Определение натуральной величины и следа отрезка примой

Прямая линия в проекциях с числовыми отметками задается своей проекцией на основную плоскость и отметками двух ее точек (рисунке 14.3). Эта прямая является прямой

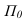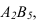общего положения. Для нее можно, как и в ортогональных проекциях, определить натуральную величину, след на плоскости и углом наклона к плоскости. Если прямую А В совместить с плоскостью вращением вокруг проекции получим натуральную величину. При этом высоты точек необходимо в масштабе чертежа отложить на перпендикулярах к проекции прямой. Прямая, соединяющая полученные точки равна истинной величине отрезка. Точка пересечения натуральной величины отрезка с ее проекцией является горизонтальным следом 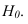. Угол между натуральной величиной и проекцией (<р), является истинной величиной угла наклона прямой к плоскости П.

Градуирование прямой

Градуирование прямой - построение на проекции прямой последовательного ряда точек с разностью отметок равной единице.

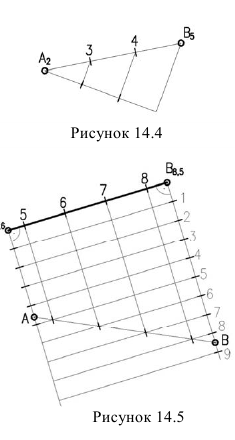
Если концы отрезков имеют целые числовые отметки, то градуирование можно произвести делением отрезка на равные части (рисунок 14.4).

В противном случае лучше использовать способ “палетки“. Для этого параллельно прямой, проводим ряд прямых, отстоящих друг от друга на равном расстоянии произвольной величины (рисунок 14.5). Принимаем их за линии уровня и на перпендикулярах находим положение концов отрезка, аналогично нахождению натуральной величины. Отрезок АВ пересекаясь с горизонталями даст положение точек с целями числовыми отметками, которые перепроицируем на проекцию прямой.  

Интервал и уклон прямой

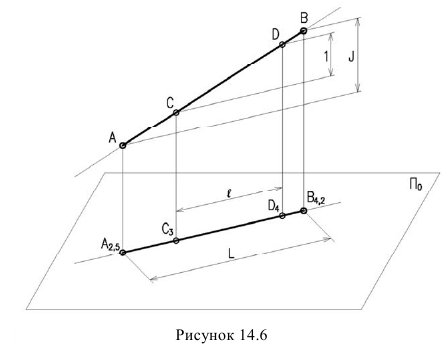
Расстояние между двумя точками горизонтальной проекции называется горизонтальным проложенном L. На рисунке 14.6 — 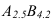А расстояние измеренное по вертикали между этими точками, т.е. разность высот называется превышением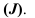

Уклоном прямой называется, отношение превышения и горизонтальному положению. На рисунке 14.6

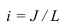
Фактически это тангенс угла наклона прямой к основной плоскости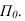

Интервал прямой - это заложение при превышении равном единице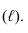

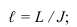
Из этих отношений видно, что интервал величина обратная уклону:

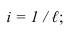
Прямую таким образом можно задать направлением прямой, проекцией одной точки и ее интервалом или уклоном.

Прямые частного положения (рисунок 14.7)

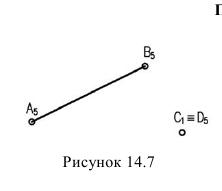
Если прямая параллельна плоскости, то она задается двумя точками с одинаковыми отметками (прямая АВ), вертикальная же прямая, т.е. перпендикулярная к плоскости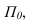 задается точкой с двумя разными отметками (прямая CD).  

Взаимное положение двух прямых

Рассмотрим условия, при которых прямые будут взаимно параллельны, пересекающиеся или скрещивающие.

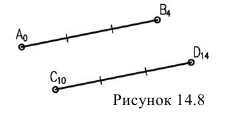
Прямые взаимно параллельны, когда их проекции параллельны, уклоны (интервалы) взаимно равны и отметки возрастают в одну сторону (рисунок 14.8).

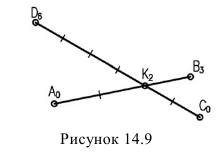
Если прямые взаимно пересекаются, то их проекции также пересекаются в точке, которая, будучи отнесена к каждой Вз из прямых имеет одинаковую отметку (рисунок 14.9).

Если проекции прямых не удовлетворяют ни одному из этих условий, прямые являются скрещивающимися.  

Проекции плоскостей. Задание плоскостей

Плоскость в проекциях с числовыми отметками, также как и в ортогональных проекциях, может быть задана проекциями трех точек, не лежащих на одной прямой, проекциями прямой и точки вне ее, проекциями двух параллельных или пересекающихся прямых или проекцией какой-либо плоской фигуры. Кроме этого, плоскость в проекциях с числовыми отметками можно задать масштабом уклонов.

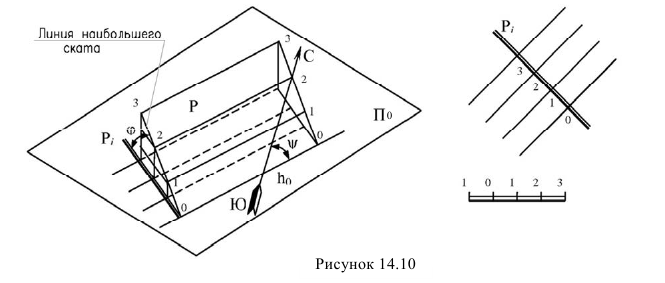
Рассмотрим рисунок 14.10.

Плоскость « является плоскостью общего положения.

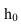- след плоскости а на плоскости П.

Ряд горизонтальных плоскостей проведенных на расстоянии равном единице рассекут плоскость а по горизонталям 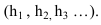Линия наибольшего ската 0-3 перпендикулярна горизонталям. Проградуированная проекция линии наибольшего ската называется масштабом уклонов плоскости а и обозначается  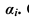Очевидно, что 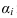перпендикулярна следу плоскости 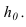Расстояние между проекциями смежных точек равно интервалу линии наибольшего ската, а следовательно и интервалу плоскости (х. Через каждую из этих точек можно провести горизонталь перпендикулярно масштабу уклонов (рисунок 14.10).

Угол между линией наибольшего ската и линией масштаба уклонов называется углом падении.

Угол между направлением главного меридиана и следом плоскости (линией простирания), измеренной против часовой стрелки называется углом простирании.

• Заказать чертежи

Взаимное положение двух плоскостей

Две плоскости в пространстве могут пересекаться и быть взаимно параллельными. Если плоскости взаимно параллельны, то масштабы их уклонов взаимно параллельны, интервалы одинаковы и возрастают в одном направлении.

Если масштабы уклонов не удовлетворяют хотя бы одному из этих условий, плоско-

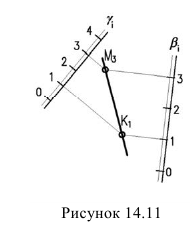
Построение линии пересечения двух плоскостей в проекциях с числовыми отметками, как и в ортогональных проекциях, основано на методе вспомогательных секущих плоскостей. В качестве вспомогательных плоскостей берутся горизонтальные, которые пересекут заданные плоскости по одноименным горизонталям. Поэтому линию пересечения двух плоскостей находят определением точек пересечения двух нар горизонталей с одинаковыми отметками (рисунок 14.11).

Если углы наклона плоскостей к плоскости проекций одинаковы, то линия пересечения располагается по биссектрисе угла. Для нахождения точки пересечения прямой с плоскостью а, необходимо через прямую провести любую вспомогательную плоскость. Определить линию пересечения плоскости у и вспомогательной. И затем определить точку пересечения прямой е построенной линией пересечения (рисунок 14.12).

Проекции поверхностей. Задание поверхностей

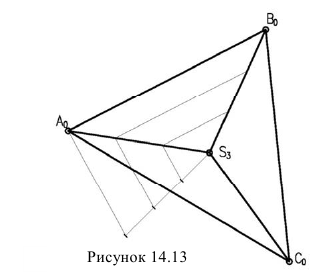
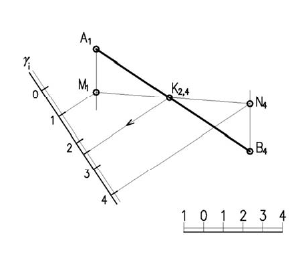
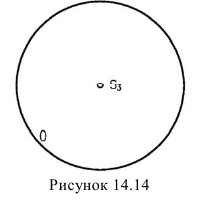
В проекциях с числовыми отметками многогранники можно задать проекциями вершин с числовыми отметками. Например, на рисунке 14.13 изображена трехгранная пирамида, основание которой лежит на предметной плоскости. Если проградуировать одно из ребер пирамиды, можно получить горизонтали граней, а, следовательно, решать различные задачи.Кривые поверхности обычно задают проекциями их горизонталей. Например, примой круговой конус может быть задан проекцией вершины и горизонталью основания (рисунок 14.14) проградиуровав, образующую можно провести ряд горизонталей конуса

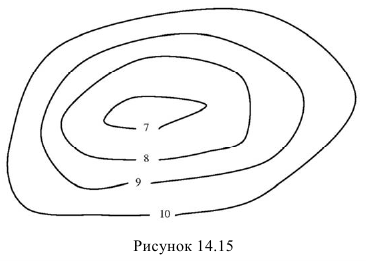
Топографическая поверхность (поверхность земли) может также задаваться горизонталями, только они являются незакономерными кривыми линиями, соединяющими точки с одинаковыми числовыми отметками (рисунок 14.15).

Пересечение поверхности плоскостью

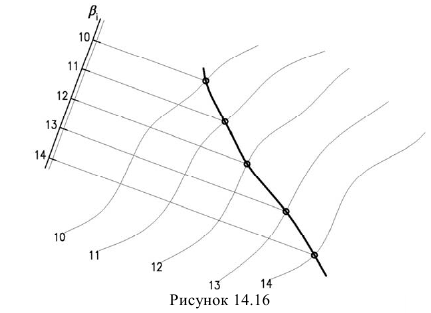
Основной задачей при выполнении проекта вертикальной планировки, является задача на построение линии пересечения поверхности плоскостью и линии пересечения двух поверхностей. Принцип построении основан также на методе вспомогательных секущих плоскостей, которые рассекают и плоскость, и поверхность но одноименным горизонталям. Определив ряд точек пересечения одноименных горизонталей, получаем линию взаимного пересечения. На рисунке 14.16 дан пример построения линии пересечения плоскости 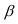с рельефом земной поверхности.  

Профиль поверхности

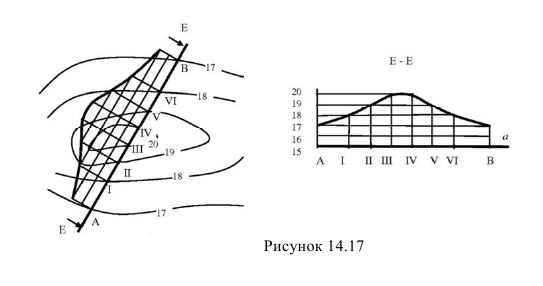
Пересечение топографической поверхности с проецирующей плоскостью называется профилем поверхности (рисунок 14.17). Секущая плоскость задана своей горизонтальной проекцией Е-Е. Для построения профиля выберем базовую горизонталь с отметкой, равной или немного ниже, минимальной отметки горизонтали местности, которая получается в сечении с плоскостью Е-Е. После проведения перпендикулярно следу плоскости линий связи, отложим на этих линиях отметки соответствующих горизонталей и соединим их плавной кривой. На профиль нанесем сетку горизонталей с учетом масштаба, принятого в плане.

Построение границ земельных работ

Пример построения сечения вертикальной плоскости рельефа с планировкой профиля:

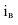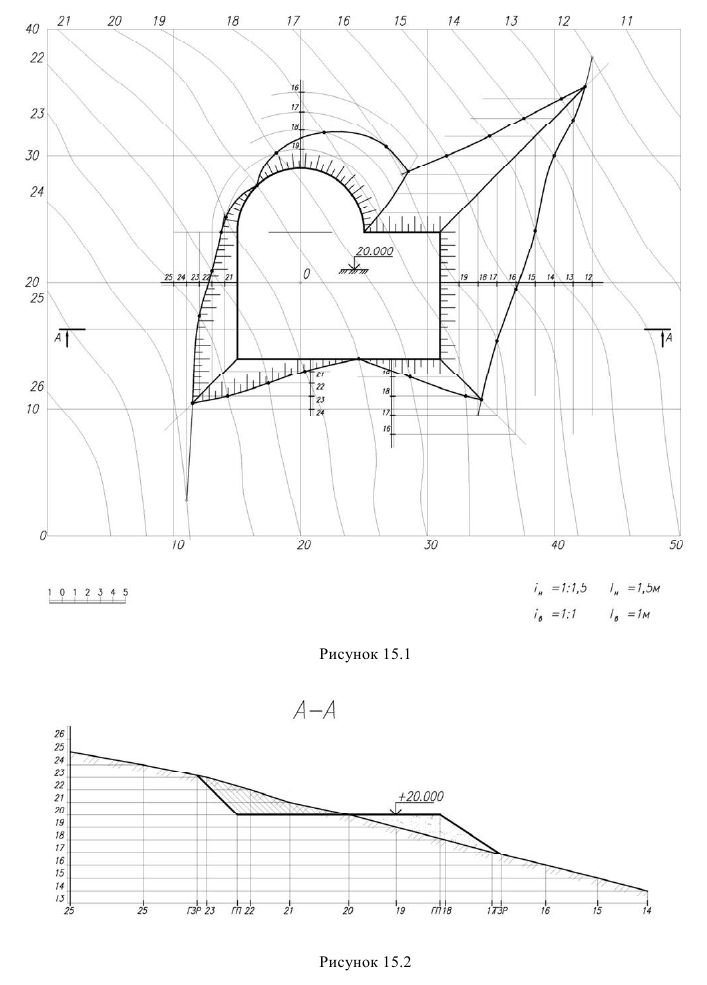
Построить линию пересечения откосов горизонтальной строительной площадки с поверхностью земли. Отметка площадки +18.00. Уклон откосов выемки = 1 : 1, насыпи 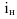= 1 : 1,5. построить сечение вертикальной плоскостью рельефа с планировкой указанной плоскостью. Масштаб изображения 1 : 200 (рисунок 15.1)

Для решения этой задачи, прежде всего, необходимо задать каждый откос площадки. Горизонталь поверхности земли 18 , является линией нулевых робот, а точки пересечения этой горизонтали с контуром площадки - точками нулевых работ. Слева от линии нулевых работ будет производиться выемка грунта, справа - насыпь. Каждый из откосов задаем масштабом уклонов, т.е. проводим линии наибольшего ската перпендикулярно кромкам площадки и градуируем их. Для этого определяем интервал выемки и насыпи : 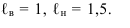Строим линии пересечения откосов между собой. Так как плоские откосы имеют одинаковый уклон, линии пересечения будут биссектрисами углов 90°. Линия пересечения конического откоса насыпи и плоского является параболой, поэтому для ее построения определяем точки пересечения одноименных горизонталей. Откос выемки будет касаться к коническому откосу, линия касания горизонтальная. Далее находим линии пересечения каждого откоса с поверхность рельефа, для чего находим точки пересечения одноименных горизонталей откосов и земной поверхности. Для нахождения промежуточных точек, лежащих на линиях пересечения откосов, необходимо находить но одной мнимой точки за пределами откоса. Полученные линии пересечения, называются "границей земляных работ". Для наглядности изображения линии бровки выделяются так называемыми "бергштрихами", выполняемыми различной длины и толщины. "Бергштрихи" проводятся перпендикулярно горизонталям, а для конического откоса по радиусам, в сторону уклона. Сечение вертикальной плоскостью построено по линии А - А. На горизонтальной линии наносят точки пересечения этой плоскостью горизонталей рельефа и линий планировки и откладывают на вертикалях их отметки (рисунок 15.2). Соединив точки рельефа, получаем сечение рельефа, а соединив точки планировки, получаем сечение планировки.