Признаки равенства прямоугольных треугольников с примерами решения

Содержание:

Признаки равенства прямоугольных треугольников:

Вы уже знаете три признака равенства треугольников. Поскольку часто приходится иметь дело с прямоугольными треугольниками, то выделяют пять признаков равенства прямоугольных треугольников. Сформулируем и докажем их.

Второй признак (по катету и прилежащему острому углу)

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Дано: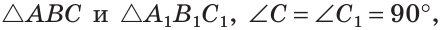

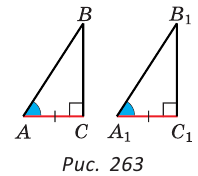
Доказать: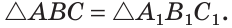

Доказательство:

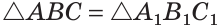по стороне и двум прилежащим к ней углам.

 

Третий признак (по катету и противолежащему острому углу)

Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Дано: 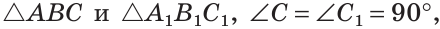 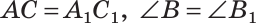 (рис. 264).

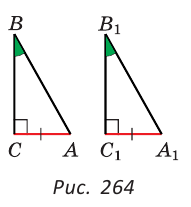
Доказать: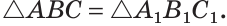

Доказательство:

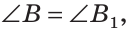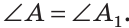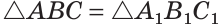Сумма острых углов прямоугольного треугольника равна 90°. Из того, что следует, что Тогда по стороне и двум прилежащим к ней углам.

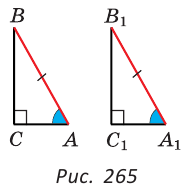
Четвертый признак (по гипотенузе и острому углу)

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Дано: 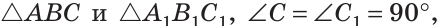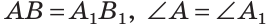(рис. 265).

Доказать: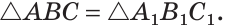

Доказательство:

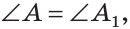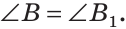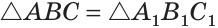Сумма острых углов прямоугольного треугольника равна 90°. Из того, что следует, что Тогда по стороне и двум прилежащим к ней углам.

Пятый признак (по катету и гипотенузе).

Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.

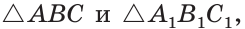
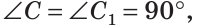
Дано: 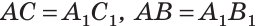(рис. 266).

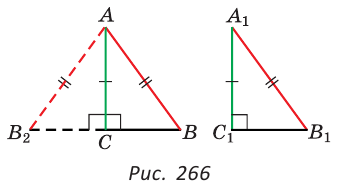
Доказать: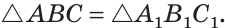

Доказательство:

Приложим треугольников А₁В₁С₁ к треугольнику АВС так, чтобы совместились равные катеты А₁С₁ и АС, а вершины В₁ и В лежали по разные стороны от прямой АС. Треугольник А₁В₁С₁ займет положение треугольника АВ₂С. Так как 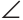B2CB — развернутый и АВ₂ = АВ, то треугольник В₂АВ — равнобедренный, катет АС — его высота. По свойству равнобедренного треугольника высота, проведенная к основанию, будет и медианой. Тогда В₂С=СВ и треугольники ABC и АВ₂С равны по двум катетам.

Отсюда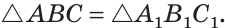

Пример:

На рисунке 267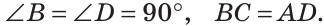

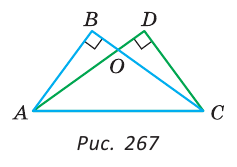
Доказать равенство треугольников: а) АВС и ADC б)  АОВ и  COD.

Доказательство:

а) Рассмотрим прямоугольные треугольники ABC и ADC. У них гипотенуза АС — общая, катеты AD и ВС равны по условию. Тогда АВС =ADC по катету и гипотенузе.

 б) Из равенства треугольников ABC и ADC следует равенство сторон АВ и CD (доказано в пункте а). Тогда АОВ =COD. по катету (АВ = CD) и противолежащему острому углу (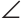AOB =COD как вертикальные).

Пример:

Дан треугольник ABC, АК и СМ — его высоты, проведенные к боковым сторонам, О — точка их пересечения (рис. 268). Доказать, что если треугольники АОМ и СОК равны, то треугольник ABC — равнобедренный.

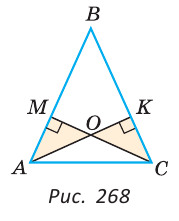
Доказательство:

Так как AOM =COK как вертикальные, то 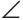MAO =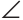KCO (сумма острых углов прямоугольного треугольника 90°). Из равенства треугольников АОМ и СОК следует равенство гипотенуз АО и СО. Треугольник АОС — равнобедренный,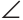OAC =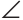OCA как углы при основании равнобедренного треугольника. Тогда 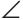BAC =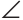BCA как составленные из равных углов. Треугольник ABC равнобедренный по признаку равнобедренного треугольника. Что и требовалось доказать.