Приведение системы сил к простейшему виду в теоретической механике

Приведение системы сил к простейшему виду:

Постановка задачи. Систему сил, заданную в прямоугольной системе координат, привести к началу координат. Найти точку пересечения центральной винтовой оси с заданной плоскостью.

Привести систему сил к центру О — означает найти главный вектор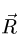

План решения:

1. Вычисляем компоненты главного вектора системы, составляя суммы проекций всех сил на оси координат: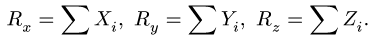

2. Находим модуль главного вектора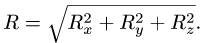

3. Вычисляем компоненты главного момента системы относительно начала координат:

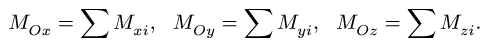
4. Находим модуль главного момента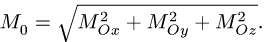

5. Определяем скалярный инвариант системы. Система сил имеет две величины, не меняющиеся при перемене центра приведения (инварианты) — главный вектор и скалярное произведение главного вектора на главный момент: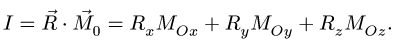

Если 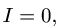то система сил приводится к равнодействующей.

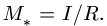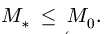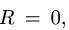6.    Находим минимальный главный момент Проверяем неравенство Если то задача решена — система приводится к паре (или уравновешена, если и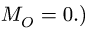

7.    Вычисляем шаг винта 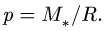 Если р < 0, то главный вектор и главный момент направлены по винтовой оси в разные стороны, если р > 0 — в одну сторону, а если р = 0, то система приводится к равнодействующей.

8.    Записываем уравнения центральной винтовой оси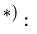

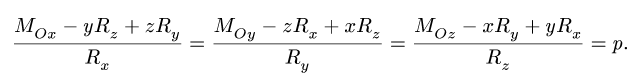
Индексы в уравнениях образуют круговую перестановку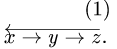

Если систему привести к любой точке на центральной винтовой оси, то главный вектор и главный момент будут лежать на этой оси и образовывать динаму.

Из трех уравнений (1) два являются независимыми.

Если один из компонентов главного вектора равен нулю, например, 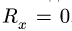, то соответствующее уравнение записывается в другой форме: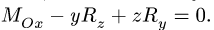

9.    Находим координаты точки А пересечения центральной оси с плоскостью ху . Если прямая параллельна плоскости ху, то такой точки не существует. Решая систему (1) при z = 0, получаем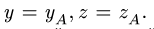 Аналогично можно найти точки пересечения центральной винтовой оси с плоскостями 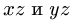(если они существуют).

10.    Проверяем решение, приводя систему к любой точке центральной винтовой оси (например, 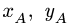). Для этого новые оси координат, параллельные старым, проводим через выбранную точку и повторяем пп. 3-4 плана. Главный момент должен быть равен минимальному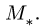

Задача:

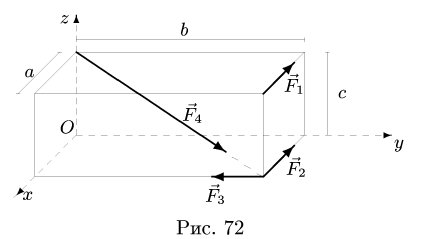
Систему сил 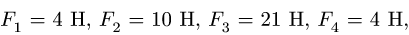приложенных к вершинам параллелепипеда, привести к началу координат (рис. 72). Найти координаты точки пересечения центральной винтовой оси с плоскостью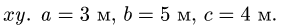

Решение

1.    Вычисляем компоненты главного вектора системы. Проекции вектора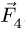, лежащего на большой диагонали параллелограмма длиной 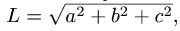вычисляем по формулам

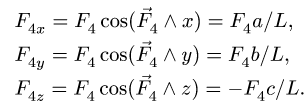
Определяем компоненты главного вектора:

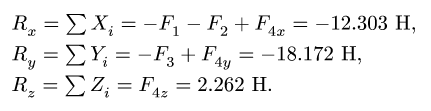
2.    Находим модуль главного вектора:

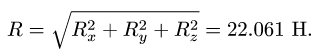
3.    Вычисляем компоненты главного момента системы сил относительно начала координат:

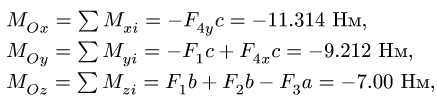
4.    Находим модуль главного момента:

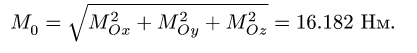
8 М.Н. Кирсанов
Гл. 4. Пространственная система сил

5.    Определяем скалярный инвариант системы:

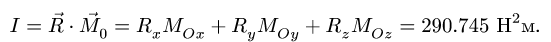
Скалярный инвариант не равен нулю, следовательно, система сил приводится к динаме.

6.    Вычисляем минимальный главный момент системы сил:

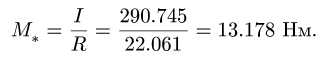
Неравенство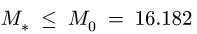 Нм выполняется. Точки, относительно которой момент системы сил меньше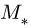, не существует.

7.    Находим шаг винта системы сил:

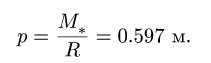
Шаг положительный, следовательно, главный момент и главный вектор направлены по центральной винтовой оси в одну сторону.

8.    Записываем уравнения центральной винтовой оси:

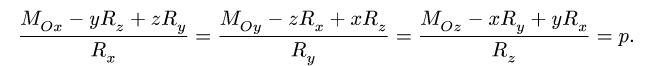
Из этих трех уравнений только два являются независимыми:

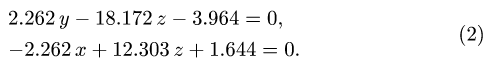
9. Находим координаты точки пересечения центральной оси с плоскостью ху. Решая систему (2) при z = 0, получаем, что

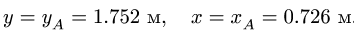
Основные результаты расчета заносим в таблицу:

10. Проверяем решение, приводя систему к точке А центральной винтовой оси. Через точку А проводим оси новой системы координат 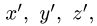параллельные исходным осям (рис. 73).

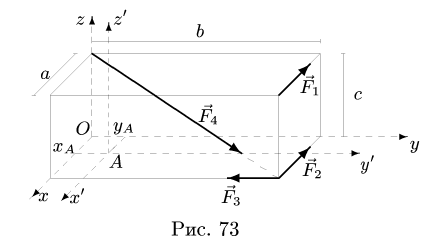
Получаем моменты заданной системы относительно новых осей координат и величину главного момента относительно центра А:

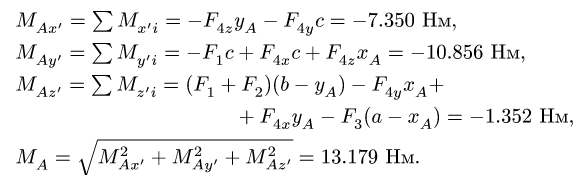
Главный момент системы 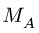относительно новой точки приведения совпадает с полученным ранее минимальным 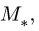что подтверждает правильность расчетов.

Замечание. Решение задачи легко проверить в системе Maple V. Приведем фрагмент программы вычислений * *.

Введены следующие обозначения: F[l] —сила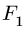 Т[1] —радиус-вектор точки приложения силы 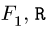— главный вектор, М — главный момент, 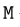— скалярный инвариант.

Здесь использована библиотека linalg. В последних версиях Maple 6,7,8 существует более совершенный пакет LinearAlgebra. В этом случае операторы скалярного и векторного произведения необходимо заменить соответственно на DotProduct и CrossProduct.