Приведение системы сил к простейшей системе в теоретической механике

Содержание:

Приведение системы сил к простейшей системе:

Приведение силы к заданному центру: Силу можно переносить параллельно самой себе в любую точку твердого тела, добавляя при этом пару сил, векторный момент которой равен векторному моменту переносимой силы относительно новой точки приложения силы.

Пусть имеем силу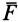

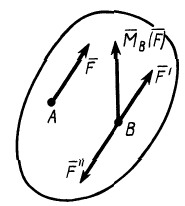
Рис. 34  

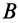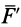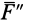Теперь докажем, что силу можно переносить на другую, параллельную линию действия. Но этот перенос следует компенсировать добавлением соответствующей пары сил. Приложим в точке тела , выбранной за центр приведения, систему двух равных по модулю, но противоположных по направлению сил и , параллельных заданной силе 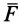. Силы 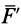и 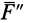 составляют систему сил, эквивалентную нулю, и ее можно добавить к любой заданной системе сил.

Пусть по модулю

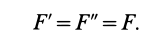
Тогда

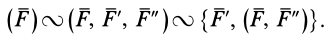
Система двух равных по модулю  и противоположных по направлению параллельных сил 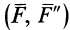составляет пару сил, которую называют присоединенной парой сил.

Итак, вместо силы 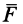, приложенной в точке 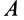, получены сила 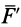, равная ей но модулю и направлению, но приложенная в точке 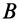, и присоединенная пара сил 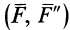, векторный момент которой

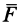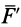Процесс замены силы силой  и парой сил 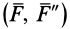называют приведением силы  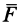к заданному центру 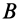. По теореме об эквивалентности пар сил пару 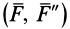можно заменить любой другой парой сил с таким же векторным моментом.

Приведение произвольной системы сил к силе и паре сил

Докажем основную теорему статики (теорему Пуансо): любую произвольную систему сил, действующих на твердое тело, можно в общем случае привести к силе и паре сил.

Такой процесс замены системы сил одной силой и парой сил называют приведением системы сил к заданному центру.

Пусть дана произвольная система сил 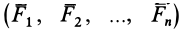, приложенных к твердому телу. Выберем произвольную точку 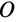тела за центр приведения и каждую силу заданной системы сил приведем к точке 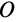(рис. 35). Получим

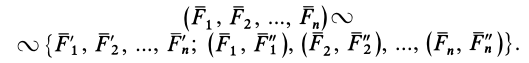
Таким образом, система из 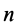сил заменена системой из 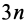сил, т. е. в точке 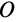приложена система сходящихся сил 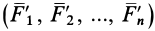и на твердое тело действует также система  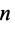присоединенных пар сил

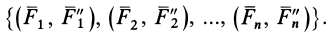
Векторные моменты присоединенных пар сил, согласно формуле (1), можно выразить через векторные моменты заданных сил:

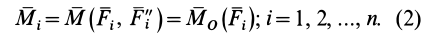
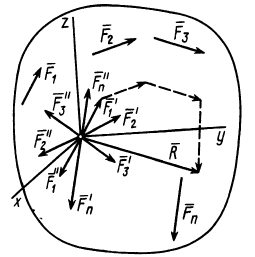
Рис.35

Систему сходящихся сил 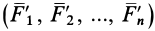заменим их равнодействующей 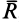, которая равна векторной сумме сил  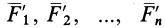 и геометрически изображается замыкающим вектором силового многоугольника, построенного на этих силах (рис. 35).

Итак,

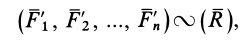
где

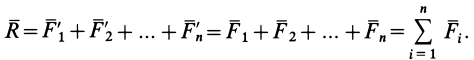
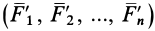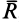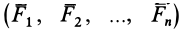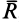Для системы сходящихся сил  сила является равнодействующей, а для заданной системы сил сила является лишь только ее векторной суммой, или главным вектором.

Главным вектором системы сил называют вектор, равный векторной сумме этих сил. Он изображается вектором, замыкающим силовой многоугольник, построенный на силах, т. е.

Систему присоединенных пар сил 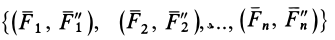 по теореме о сложении пар сил можно заменить одной парой сил 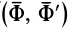с векторным моментом 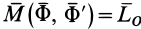, который называют главным моментом. Главный момент равен сумме векторных моментов присоединенных пар. Учитывая формулу (2), для 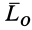 имеем

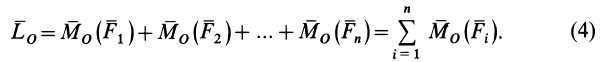
Индекс 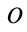означает, что за центр приведения взята точка .

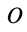Итак, главным моментом системы сил относительно точки 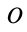тела называют сумму векторных моментов всех сил системы относительно этой точки.

Главный момент системы сил является вектором, замыкающим векторный многоугольник, образованный при сложении векторных моментов сил системы относительно выбранного центра.

Таким образом, доказана основная теорема статики: любую систему сил, действующих на твердое тело, можно привести к силе, равной главному вектору системы сил, и паре сил, векторный момент которой равен главному моменту системы сил относительно точки, выбранной за центр приведения.

В краткой форме эту теорему можно выразить так:

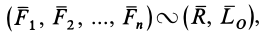
т. е. каждую систему сил можно привести к главному вектору и главному моменту относительно произвольного центра. Следует учитывать, что это условная формулировка основной теоремы. Главный момент характеризует действие на тело пары сил 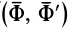(рис. 36), лежащей в плоскости, перпендикулярной главному моменту.

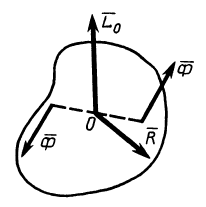
Рис. 36

Приведение плоской системы сил

Плоской системой сил, приложенных к твердому телу, называют такую систему сил, линии действия которых лежат в одной плоскости. Основная теорема статики справедлива для любой системы сил. Она справедлива и для плоской системы сил, действующих на твердое тело: любую плоскую систему сил можно в общем случае привести к силе и паре сил.

Для плоской системы сил главный вектор 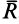лежит в плоскости действия сил, если за центр приведения выбрать точку в плоскости действия сил. Все присоединенные пары сил тоже лежат в этой плоскости, а следовательно, векторные моменты этих пар перпендикулярны ей и взаимно параллельны. Главный момент 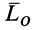, характеризующий векторный момент пары сил, эквивалентный присоединенным парам, перпендикулярен главному вектору. Он является векторной суммой параллельных векторов.

В этом случае главный момент равен сумме алгебраических моментов присоединенных пар и, следовательно, сумме алгебраических моментов сил относительно центра приведения.

Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента. Алгебраическим главным моментом 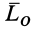 плоской системы сил относительно центра приведения, лежащего в плоскости действия сил, называют сумму алгебраических моментов этих сил относительно центра приведения.

• Заказать решение задач по теоретической механике

Формулы для вычисления главного вектора и главного момента

Для любой системы сил 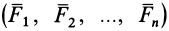 главный вектор 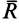является векторной суммой этих сил:

а главный момент 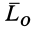— суммой векторных моментов сил относительно центра приведения:

Главный вектор 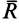геометрически изображается замыкающей силового многоугольника, построенного на заданных силах. Проецируя обе части векторного равенства (3') на координатные оси, для произвольной пространственной системы сил получаем

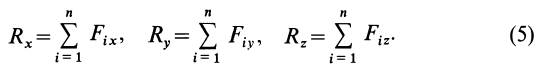
По проекциям определяют модуль главного вектора и косинусы его углов с осями координат:

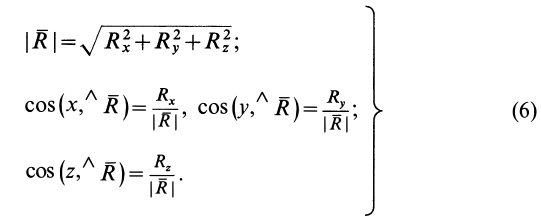
Главный момент 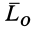геометрически тоже изображается замыкающей векторного многоугольника, построенного на векторных моментах сил относительно центра приведения. Проецируя обе части векторного равенства (4') на прямоугольные оси координат и используя связь момента силы относительно оси с проекцией векторного момента этой силы относительно точки на оси, имеем

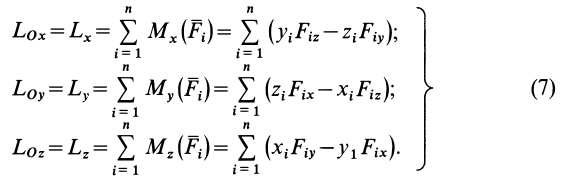
Модуль главного момента и косинусы его углов с осями координат равны

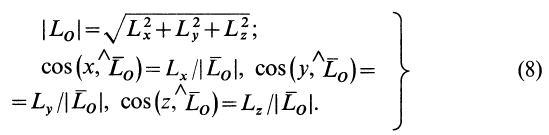
Если выбрать ось 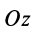перпендикулярно плоскости действия плоской системы сил, а ос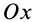и  и 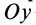— в плоскости сил, то главный вектор 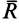будет лежать в плоскости 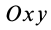и, следовательно, для плоской системы сил

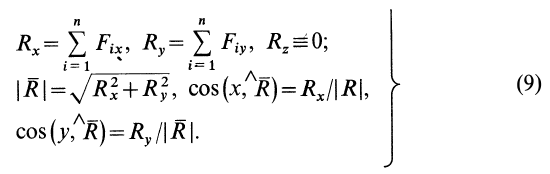
Главный момент плоской системы сил перпендикулярен главному вектору и, следовательно, параллелен оси 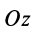. Тогда

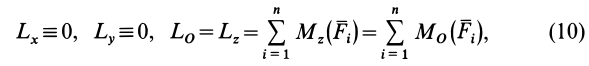
где 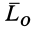— алгебраический главный момент.