Приведение системы сил к данной точке в теоретической механике

Приведение системы сил к данной точке:

Всякая сила, приложенная к твердому телу, эквивалентна такой же силе, но приложенной в другой точке тела, и паре сил с моментом, равным моменту первой силы относительно точки приложения второй

Метод Пуансо

Согласно теореме, действие силы на твердое тело не изменится, если эту силу перенести в какую-либо другую точку тела, лежащую на линии действия этой силы.

Докажем, что действие силы на твердое тело не изменится, если эту силу перенести в точку тела, не лежащую на линии действия данной силы, но при этом одновременно добавить пару сил с моментом, равным моменту данной силы относительно той точки, в которую мы эту силу перенесли.

Пусть дана сила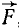

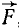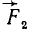Но силы и представляют собой пару сил, а потому всю систему можно рассматривать как силу 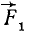, геометрически равную данной силе F, но приложенную в точке О, и пару сил 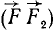. Момент этой пары равен моменту данной силы относительно точки О. Пару мы можем поворачивать (рис. 49, в), переносить в другое место или заменять эквивалентной парой, а сила 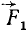, равная данной силе 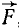останется приложенной в точке О.

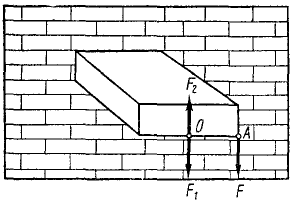
Рис. 50

Такое перенесение силы является формальным, но может соответствовать физической сущности явления. Пусть, например, сила 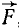, приложенная в точке А, действует на металлический брусок, заделанный в каменную стену (рис. 50). Перенеся силу в точку О с добавлением пары сил, мы можем рассматривать ее как силу, приложенную в точке О и изгибающую брусок, а пару 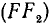— как скручивающую его. На этом примере мы видим, что сила 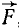по своему действию эквивалентна силе 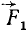вместе с парой .

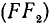Система сил, приложенных к твердому телу, эквивалентна главному вектору, приложенному в произвольной точке тела, и главному моменту относительно этой точки.

• Заказать решение задач по теоретической механике

Приведение системы сил к точке

Пусть к твердому телу приложена произвольная система сил, т. е. такая система, на силы которой, на точки их приложения и на линии действия не наложено никаких ограничений. Какую-либо из точек тела, безразлично которую, назовем центром приведения и, следуя методу Пуансо, приведем к этой точке каждую из сил системы.

Тогда получим в центре приведения пучок сил (каждая из которых по величине и направлению равна одной из сил заданной системы) и систему пар. Момент каждой из этих пар равен моменту одной из сил заданной системы относительно центра приведения.

Главным вектором системы сил называют вектор, равный сумме векторов всех сил системы: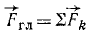 

Складывая все силы пучка, мы заменим их одним вектором, приложенным в выбранном нами центре приведения и равным сумме векторов всех сил, перенесенных в эту точку. Его называют главным вектором системы сил:
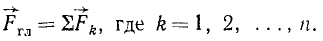       (27)

При перенесении сил системы к центру приведения мы не меняли ни величин, ни направлений этих сил, поэтому главный вектор системы сил не зависит от того, какую точку тела мы приняли за центр приведения. Главный вектор является инвариантом (неизменной величиной) данной системы сил.

Главным моментом системы сил называют вектор, равный сумме векторов моментов всех сил системы относительно данной точки

Чтобы сложить пары сил, получившиеся при приведении по методу Пуансо всех сил системы к выбранному нами центру, достаточно геометрически сложить их моменты. Но моменты этих пар равны моментам соответствующих сил заданной системы относительно центра приведения. Поэтому, чтобы сложить эти пары, достаточно взять сумму моментов всех сил системы относительно центра приведения. Мы обозначим эту сумму через 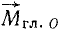и назовем главным моментом системы сил относительно центра О, или, коротко, главным моментом:

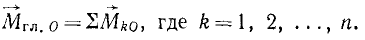       (28)

В отличие от главного вектора главный момент системы сил не является инвариантом и зависит от выбранного нами центра приведения. Меняя центр приведения, мы изменили бы и моменты сил системы относительно этого центра, отчего изменился бы и главный момент.

Итак, всякая система сил, приложенных к твердому телу, эквивалентна одной силе, называемой главным вектором, равной геометрической сумме всех сил системы и приложенной в любой точке тела (в центре приведения), и одной паре, момент которой называют главным моментом и который равен сумме моментов всех сил системы относительно этой точки. Такое преобразование системы сил, не изменяя действия ее на твердое тело, значительно упрощает ее изучение.