Приведение двух параллельных сил к равнодействующей в теоретической механике

Содержание:

Приведение двух параллельных сил к равнодействующей:

Две параллельные силы, направленные в одну сторону, всегда имеют, равнодействующую, направленную в ту же сторону и по модулю равную сумме модулей слагаемых сил. Линия действия равнодействующей делит расстояние между линиями действия слагаемых сил внутренним образом на части, обратно пропорциональные модулям слагаемых сил

Сложение двух параллельных сил, направленных в одну сторону

Если векторы сил параллельны между собой, то линии действия их не пересекаются и их нельзя складывать по правилу сложения сил. Для приведения параллельных сил к равнодействующей существуют другие правила, выводом которых мы теперь займемся.

Пусть на твердое тело (рис. 22, а) действуют две силы:

Приложим к тому же телу в точках А и В две равные силы и (рис. 22, б), направленные по прямой AB в противоположные стороны. Силы и взаимно уравновешивают друг друга, наличие таких сил эквивалентно их отсутствию, а следовательно, система четырех действующих на данное тело сил (, , и ) эквивалентна двум данным силам и . Сложив затем силы и , приложенные к телу в точке А, мы заменим их одной силой 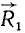, приложенной к той же точке А. Сложив силы и , приложенные к телу в точке В, мы заменим их одной силой 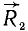. Силы и эквивалентны системе сил (F₁, , и ), а следовательно, они эквивалентны двум силам ( и F₂).

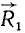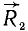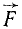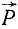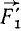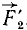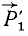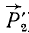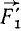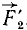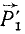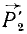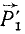Перенесем силы и в точку D пересечения их линий действия (рис. 22, в) и там разложим каждую из них на две составляющие, параллельные силам и. Мы получим четыре силы (, , и), приложенные к точке D и эквивалентные системе сил ( и ), причем = , =, =, = . Заметим, что силы и 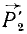равны между собой по величине и действуют по одной и той же прямой в противоположные стороны, а потому они уравновешивают друг друга, т. е. наличие этих сил эквивалентно их отсутствию, и мы можем отбросить силы и . Останутся только две силы, приложенные в одной и той же точке D, а именно , равная данной силе , и , равная силе .

Таким образом, систему двух параллельных сил (, ), приложенных в разных точках А и В твердого тела, мы заменили эквивалентной системой таких же сил, но приложенных к одной точке D. Очевидно, что равнодействующая этой системы приложена в той же точке D, направлена в ту же сторону, что и слагаемые силы, а по .модулю равна сумме модулей этих сил:

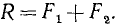    (10)

Перенесем равнодействующую 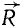по линии действия в точку С, лежащую на прямой AB (рис. 22, г). Из подобия полученных треугольников ACD и BCD, соответственным силовым треугольникам (см. рис. 22, в), можно написать

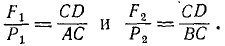
Деля первую пропорцию на вторую и принимая во внимание, что P₁=P₂, получим

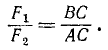    (11)

Следовательно (рис. 22, д), две параллельные силы и , направленные в одну сторону, приведены к одной равнодействующей 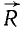, направленной в ту же сторону и по модулю равной сумме модулей слагаемых сил. Линия действия равнодействующей R лежит между линиями действия слагаемых сил и делит расстояние AB на части, обратно пропорциональные модулям слагаемых сил.

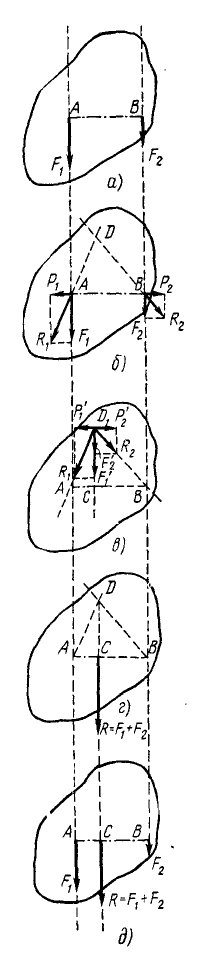
Рис. 22

Две неравные параллельные силы, направленные в противоположные стороны, имеют равнодействующую, направленную в сторону большей силы и по модулю равную разности модулей слагаемых сил. Линия действия равнодействующей делит расстояние между линиями действия слагаемых сил внешним образом на части, обратно пропорциональные модулям слагаемых сил

Сложение параллельных сил, направленных в противоположные стороны

Параллельные силы, направленные в противоположные стороны, могут быть приведены к равнодействующей только в том случае, если модули слагаемых сил не равны между собой.

Пусть на твердое тело (рис. 23, а) действуют две силы: приложенная к точке А, и , приложенная к точке В. Линии действия этих сил параллельны, но направления противоположны. По величине силы не равны, пусть F₁ > F₂. Приложим к тому же телу в точках А и В две взаимно уравновешенные силы и (рис. 23, б).

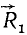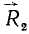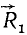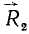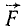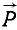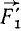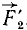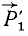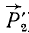Сложив затем силы и , приложенные к точке А, мы заменим их одной силой . Сложив и заменим их силой . Перенесем силы и в точку D пересечения их линий действия (рис. 23, в) и там разложим каждую из них на две составляющие, параллельные силам   и . В точке D мы получим пучок четырех сил (, , и), эквивалентный системе двух данных параллельных сил ( и ), причем F1 = 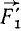= , =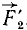, 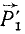=, 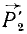= .Отбросим взаимно уравновешенные силы P'1 и P2. Тогда в точке D останутся лишь две силы 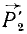и . Равнодействующая этой системы сил приложена в точке D, направлена в сторону большей силы, а по модулю равна разности модулей слагаемых сил:
P = F₁-F₂.       (10')

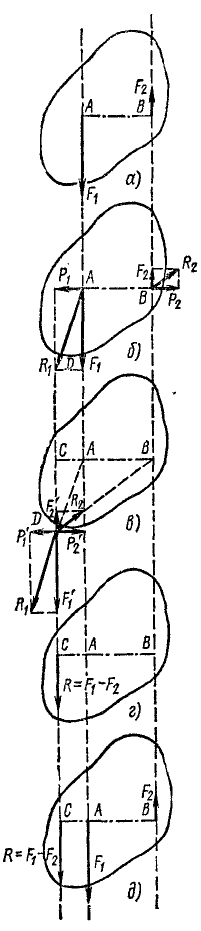
Рис. 23

Перенесем равнодействующую P по линии действия к точке С, лежащей на прямой AB (рис. 23, г). Из подобия треугольников ACD, BCD и соответствующих силовых треугольников можно написать пропорции

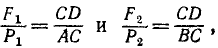
откуда 

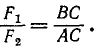  (11)

Следовательно (рис. 23, д), две неравные параллельные силы F₁ и F₂, направленные в противоположные стороны, приведены нами к одной равнодействующей R, направленной в сторону большей силы и по модулю равной разности модулей слагаемых сил. Линия действия равнодействующей лежит за линией действия большей силы и делит расстояние между слагаемыми силами на части, обратно пропорциональные модулям сил.

Из равенств (10) или (10^/) и (11) можно получить следующие производные пропорции, полезные при решении задач:
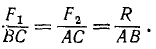    (12)

Заметим, что теоремы о проекциях равнодействующей пучка сил (см. § 6), конечно, остаются справедливыми и для проекций равнодействующей параллельных сил, так как направляющие косинусы параллельных сил одинаковы.

Данную силу можно разложить на две, ей параллельные, для которых данная сила является равнодействующей.

• Заказать решение задач по теоретической механике

Разложение силы на параллельные составляющие

Задача приведения к равнодействующей двух параллельных сил имеет всегда однозначное решение. Обратная задача — разложение данной силы R на две, ей параллельные, 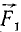 и 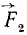-неопределенная и может иметь сколько угодно решений. Задача становится определенной, если заданы расстояния AC и BC до линии действия этих сил или заданы расстояние (AC, BC или АВ) и модуль одной из сил. Имея заданный величины, можно определить искомые по выведенным формулам:

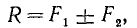     (10, 10^/)

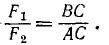    (11)

Задача №1

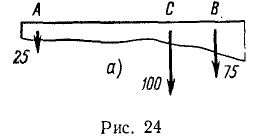
Вес (G=100 кГ) балки приложен в точке С. Как расположить опоры А и В, чтобы давление балки на опору В равнялось 75 кГ?

Решение. Для получения ответа достаточно подставить числовые данные в формулы (10), (10^/) и (11). Но задача не имеет однозначного решения. Опору В можно поместить в любой точке балки, причем: 1) если балка давит на опору В сверху вниз (рис. 24), то опора А должна быть расположена по другую сторону от C на расстоянии, определяемом из пропорции: ЛС:ВС = 75:25, т. е. на расстоянии AC=3BC: 2) если же балка давит на опору В снизу вверх, то опора А должна быть расположена между C и В на расстоянии от С, определяемом из пропорции:
AC: BC = 75:175, т. е. на расстоянии 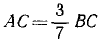. Чтобы задача стала определенной, надо в условии указать вверх или вниз направлено давление балки на точку В и задать одно из расстояний (АС, BC или АВ).

Задача №2

Однородный стержень AB весом G = 100 кГ опирается одним концом на гладкий горизонтальный пол, другим — на гладкую плоскость, наклоненную под углом 30° к горизонту. У конца В стержень поддерживается веревкой с грузом P, перекинутой через блок С. Отрезок .веревки BC параллелен наклонной плоскости. Пренебрегая трением на блоке, определить груз P и давления N_А и N_В на пол и на наклонную плоскость (рис. 25, а).

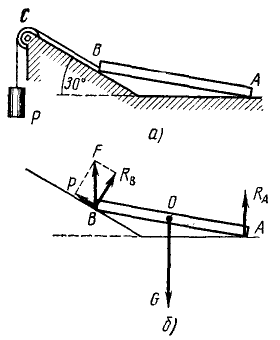
Рис. 25

Решение. Одна из искомых сил действует на пол, другая —на наклонную плоскость, третья приложена к грузу. Но груз поддерживается веревкой, и натяжение веревки равно весу P груза. Блок C меняет направление силы натяжения веревки. Поэтому на точку В стержня действует в направлении BC сила P. На ту же точку В действует реакция R_в, по принципу равенства действия и противодействия равная и противоположная искомому давлению стержня на наклонную плоскость; на точку А действует реакция R_А, равная и противоположная давлению N стержня на пол. Таким образом, рассмотрев равновесие стержня А В, мы сможем определить все искомые силы.

На стержень AB действуют следующие силы: 1) вес G, приложенный в середине стержня и направленный вниз; 2) реакция Рд пола в точке А, направленная вертикально (перпендикулярно виртуальным перемещениям); 3) в точке В натяжение P нити, направленное по нити, и реакция R_В наклонной плоскости, перпендикулярная к плоскости. Но если мы сложим эти две силы по правилу параллелограмма и заменим их одной силой F (рис. 25, б), то мы можем рассматривать балку как находящуюся в равновесии под действием трех сил: G, R_А, F. Известно, что две из этих сил (G и Ra) вертикальны, следовательно, вертикальна и третья сила F.

Так как вес стержня приложен в его середине, а силы F и R_А-по концам, то, следовательно, 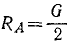и .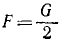

Из чертежа видно, что 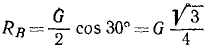; 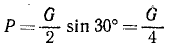.  Искомые давления N_A и N_В равны и противоположны реакциям  R_А  и R_В.

Ответ. P = 25 κΓ∙, N_А = 50κΓ; N_В = 43,3 кГ.

Задача №3

Чтобы поднять лебедкой груз (заводское оборудование) весом G=6T на второй этаж заводского корпуса, не допустив возникновения горизонтальных усилий на стены здания, монтажники перекинули трос от лебедки L к грузу G через два блока, находящихся на одной вертикали, причем блок O₁ прикреплен к полу первого этажа (рис. 26, а), а блок O₂— к потолочной балке второго этажа. Определить силу, действующую на балку в точке C крепления блока O₂, и реакции от действия этой силы на опоры А и В балки, если AB= 12 м, AC = 4м и груз прямолинейно.

Решение. Рассмотрим сначала равновесие блока O₂, а затем равновесие балки АВ.
На блок O₂ действуют следующие силы (рис. 26, б): 1) сила натяжения ветви троса, на которой висит груз, равная весу груза (6 Т) и направленная по этой ветви вниз; 2) сила натяжения ветви троса, направленная к блоку O₁; эта сила тоже равна 6 Т, так как блок не меняет величину силы; 3) реакция в оси. блока O₂. Очевидно, что реакция в оси направлена вертикально вверх и равна 12 Т, так как она уравновешивает две направленные вниз силы по 6 T каждая. Следовательно, на балку AB в месте C крепления блока действует сила, равная 12 T и направленная вниз.

При рассмотрении равновесия балки AB мы, кроме этой силы в 12 T, учтем и вызванные ею реакции в точках опоры А и В (рис. 26, в). Реакции в опорах равны и противоположны давлениям, и мы находим их из пропорции (12):

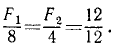
Ответ. Сила, действующая на балку в точке C= 12 Т; F₁ =8 Т; F₂ = 4T.