Принцип относительности Галилея в физике - формулы и определение с примерами

Содержание:

Принцип относительности Галилея:

Одной из причин открытия принципа относительности является движение Земли, точнее, гипотеза о вращении ее вокруг своей оси. Возникает такой вопрос: если Земля вращается вокруг своей оси, почему мы не чувствуем это в экспериментах, проведенных на ее поверхности? Занимавшиеся этой проблемой в средние века ученые Николай Орема (XIV век) и Алавуддин Али ал-Кушчи (XV век) пришли к следующему заключению: вращение Земли не влияет на проведенные на ее поверхности эксперименты.

Представим себе, что вы с одноклассниками находитесь в каюте с затемненными внешними окнами в большом корабле. Кто-то из одноклассников интересуется, корабль находится в покое или плывет? Как можно это определить, не выходя на внешнюю палубу? Один из учеников предлагает: «Проведем такой опыт. Возьмем какой-нибудь предмет, бросим сверху вниз  вертикально на пол. Если корабль находится в покое, предмет упадет вертикально. Если двигается, то, учитывая, что за период падения предмета корабль передвинется вперед, предмет упадет немного назад. При проведении экспериментов все предметы упали вертикально, на одно и то же место. Значит, сделаем вывод, что корабль находится в покое.  Однако выйдя на палубу мы увидим, что корабль равномерно двигается по воде. Следовательно, механические эксперименты проводятся с одинаковым результатом, что в учебном классе, что в вагоне или корабле, которые двигаются прямолинейно и равномерно.

Пусть скорость человека относительно вагона будет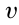

Опыты показали, что в разных инерциальных системах отсчета полный оборот минутной стрелки часов происходит за одинаковый период времени.
Перемещение тел в системах отсчета не будет одинаковым.

Перемещение идущего по движущемуся вагону человека относительно вагона будет меньше, чем перемещение этого человека относительно Земли. Масса тела в неподвижной или двигающейся прямолинейно и равномерно инерциальной системе отсчета будет одинакова.

Таким образом, в инерциальных системах отсчета время, масса, ускорение и сила будут одинаковыми (инвариантными).

Если в системе отсчета, которая находится в покое, сила равна 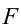, масса равна 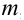, ускорение равно 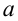, то в системе с прямолинейным и равномерным движением будет соответственно: 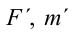и . И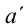з-за того, что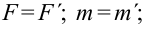 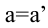  второй закон Ньютона выражается в виде: .

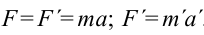Отсюда вытекает, что законы Ньютона правомерны во всех инерциальных системах отсчета.

Принцип относительности Галилея в общем виде можно сформулировать следующим образом:

• Во всех инерциальных системах отсчета все механические процессы протекают одинаково.

Однако нельзя забывать следующее. Мы знаем, что прямолинейное равномерное движение встречается очень редко. Это означает, что очень редко существуют инерциальные системы отсчета, поэтому нужно помнить, что существуют системы, близкие к инерциальным системам отсчета. Землю мы рассматриваем как инерциальную систему отсчета, хотя она вращается вокруг своей оси и вокруг Солнца, а при вращательном движении всегда существует ускорение. Несмотря на это, Земля считается инерционной системой отсчета. Причина этого в том, что ускорение Земли очень маленькое. Например, это ускорение на экваторе равно 0,035 м/с² и является очень маленькой величиной по сравнению с ускорением свободного падения, поэтому им можно пренебречь. А при вращении Земли вокруг Солнца ускорение еще меньше, поэтому Землю можно считать инерционной системой отсчета.

Tакже поезд, который двигается относительно Земли прямолинейно и равномерно, можно отнести к инерционным системам отсчета. 
Учитывая вышесказанное можно считать, что в системах, двигающихся прямолинейно и равномерно, законы Ньютона будут действительными. 

Что же происходит, если система отсчета будет двигаться криволинейно или с ускорением? Такие системы называются неинерцальными системами отсчета. Как можно использовать законы Ньютона в неинерциальных системах отсчета? Давайте вспомним причины появления ускорения. Причина появления ускорения – это сила. Значит, чтобы применить второй закон Ньютона, наряду с силами, действующими на тело со стороны других тел, вводим величину инерционная сила.

Инерционная сила возникает не в результате действия на тело со стороны других тел, а в результате движения с ускорением системы отсчета. В таком случае второй закон Ньютона имеет вид:

Чтобы найти выражение для инерционной силы, воспользуемся разницей абсолютного значения ускорения 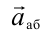и относительного значения ускорения 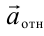. Выражение для инерционной силы приобретает следующий вид:

Сказанное рассмотрим на примере.

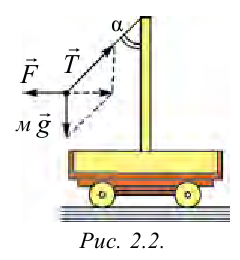
На маленькой тележке установлена колонна, к которой подвешен маятник, как показано на рисунке 2.2. Тележка двигается с постоянным ускорением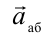 относительно Земли. Маятник неподвижен относительно тележки: 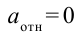. На маятник действуют силы: 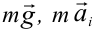и  – сила упругости нити, на которой висит маятник. Но эти силы не дают ускорения маятнику. Чтобы выполнялся второй закон Ньютона, нужно ввести инерционную силу 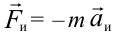. Тогда

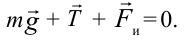
Значит, второй закон Ньютона выполняется условно. Угол наклона маятника: .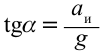

Основы специальной теории относительности

Роль скорости распространения света в вакууме настолько важна в физике и технике, а современные методы ее измерения настолько надежны, что в 1983 г. было принято решение считать значение этой скорости точным. Оно равно 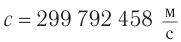. Эксперименты показывают, что с такой скоростью распространяется в вакууме не только видимый свет, но и любое электромагнитное излучение — от радиоволн до гамма-излучения.

Развитие науки и техники позволило физикам уже на рубеже XIX—XX вв. провести достаточно точные измерения скорости света. Как оказалось, скорость света в вакууме не зависит ни от скорости движения приемника света, ни от скорости источника, излучающего свет.

Эти удивительные экспериментальные результаты привели физиков к пересмотру представлений о свойствах пространства и времени. Была создана специальная теория относительности () — раздел физики, в котором изучаются свойства пространства и времени, а также законы движения тел при скоростях, сравнимых со скоростью света.

Специальная теория относительности называется также релятивистской теорией (от лат. relativus — относительный). Явления, происходящие при скоростях, сравнимых со скоростью света, характеризующие их величины (скорость, энергия, импульс и т. д.) и законы этих явлений тоже называются релятивистскими.

Заметим, что помимо специальной теории относительности () имеется и общая теория относительности (ОТО), которая обобщает на случай, когда существенны гравитационные явления.

В повседневной жизни и в современных технологиях (даже космических) мы не встречаемся с релятивистскими скоростями. Зачем же изучать теорию относительности? Для этого имеется целый ряд причин.

Во-первых, основную информацию об окружающем мире мы получаем с помощью зрения, непосредственно воспринимая световое излучение. Таким образом, «самый релятивистский» объект природы — свет играет важнейшую роль в жизни каждого человека.

Во-вторых, как показывает весь накопленный опыт, скорость света в вакууме имеет фундаментальное, выделенное значение: ни один сигнал не может распространяться, ни одна частица не может двигаться быстрее света.

В-третьих, релятивистская теория необходима для объяснения явлений в атомной и ядерной физике, в физике элементарных частиц. Без использования законов  невозможно и создание ускорителей элементарных частиц.

В-четвертых, релятивистская теория играет важную роль в изучении Вселенной. Обнаружены галактики, движущиеся с огромными скоростями. Без релятивистской теории нельзя объяснить свойства таких астрономических объектов, как «черные дыры», нейтронные звезды, пульсары.

Наконец, каждый человек должен иметь современные представления о пространстве и времени, об относительных и абсолютных явлениях, о таких удивительных релятивистских эффектах, как относительность одновременности, замедление времени и сокращение длины при движении объектов.

Принцип относительности Галилея и электромагнитные явления

Система отсчета, относительно которой все тела покоятся или движутся с постоянной скоростью при отсутствии воздействия на них, называется инерциальной ().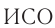

Принцип относительности Галилея: во всех 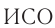все механические явления при одинаковых начальных условиях происходят одинаковым образом. Классический закон сложения скоростей: 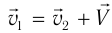, где 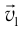 — скорость движения тела относительно 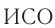-1, 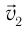—относительно 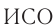-2, 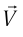—скорость 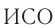-2 относительно ИСО-1.

Создание специальной теории относительности исторически связано с развитием электродинамики — науки об электрических и магнитных явлениях. За два столетия, которые отделяли физику Галилея и Ньютона от физики Максвелла и Герца, в ней накопилось огромное количество новых научных фактов. В то же время представление о мироздании базировалось на механической картине мира, основанной на механике Галилея — Ньютона (классической механике).

Как известно, в классической механике такие понятия, как координата, скорость, траектория тела, являются относительными — они изменяются при переходе от одной 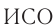 к другой. В то же время, некоторые понятия и величины в классической физике считались абсолютными. Например, как само собой разумеющееся принималось положение об абсолютности времени (ход времени везде одинаков). Очевидным следствием этих представлений является классический закон сложения скоростей. Согласно этому закону при переходе к 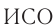, которая движется со скоростью 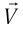навстречу телу, модуль скорости тела становится больше на величину, равную 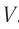. Это означает, что в механике Галилея — Ньютона не существует максимально возможной (предельной) скорости.

Такие представления согласовывались как с повседневным опытом, так и с экспериментами в механике, акустике, гидродинамике и т. д.

Однако электромагнитные процессы происходят со скоростями, сравнимыми со скоростью света, т. е. гораздо большими, чем скорости движения тел, с которыми имеет дело механика. В связи с этим возникают вопросы: будет ли справедлив принцип относительности Галилея (важнейший принцип классической механики) для электромагнитных явлений? Зависит ли скорость света в вакууме от движения источника и/или приемника излучения, как это должно быть по классической теории? Существует ли в природе предельная скорость? Для ответа на эти вопросы были необходимы новые эксперименты.

Рассматривая проблему распространения электромагнитных волн (света), полезно обратиться к хорошо изученным закономерностям поведения звуковых волн. Они могут распространяться только в упругой среде — газообразной, жидкой или твердой. Естественно принять предположение, что и для распространения света необходима некоторая среда. Ее назвали мировым эфиром. При таком подходе решающим становится вопрос о скорости света, измеренной наблюдателем, который движется относительно эфира.

Вернемся к аналогии со звуком. Пусть скорость звука в покоящейся среде равна 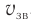. Эксперимент показывает, что при измерении скорости звука устройством, которое движется относительно этой среды со скоростью 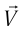навстречу звуку, получается величина, равная .

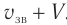А что получится для распространения света? Зависит ли скорость света от движения лаборатории, в которой проводятся измерения этой скорости? В качестве такой быстро движущейся лаборатории 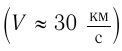было предложено использовать Землю. Если считать, что Земля при своем обращении вокруг Солнца движется сквозь неподвижный эфир, то в лаборатории, находящейся на Земле, следует ожидать появления так называемого «эфирного ветра» (подобно тому, как возникает встречный поток воздуха при езде на мотоцикле в безветренную погоду). Как повлияет «эфирный ветер» на скорость света в системе отсчета «Земля»?

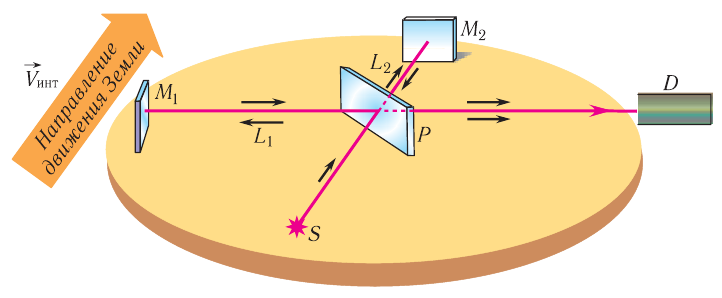
Рис. 100. Опыт Майкельсона — Морли

В 1887 г. американские физики А. Майкельсон и R Морли провели эксперимент, точность измерений в котором была достаточной для обнаружения влияния «эфирного ветра».

Разберем принципиальную схему их экспериментальной установки, получившей название интерферометр Майкельсона (рис. 100). Он состоял из оптического устройства, расположенного на массивной каменной платформе, плавающей в бассейне с ртутью. Такая конструкция практически исключала влияние механических колебаний платформы на оптические процессы. 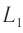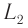Свет от источника с помощью полупрозрачной пластины делился на два взаимно перпендикулярных луча и  (см. рис. 100). Лучи отражались от зеркал 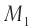и 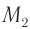, а затем сводились вместе с помощью той же полупрозрачной пластинки 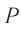и попадали на детектор 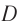. В результате сложения этих лучей получалась интерференционная картина (чередующиеся темные и светлые полосы, наблюдавшиеся с помощью детектора). Ожидалось, что эта картина будет существенно зависеть от ориентации интерферометра по отношению к его скорости  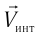 относительно «неподвижного» эфира (см. рис. 100). Действительно, если один из пучков направлен вдоль скорости 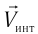, а второй — перпендикулярно ей, то «эфирный ветер» будет неодинаковым для этих лучей. Соответственно, будет различным и время прохождения света для луче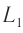й и 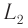от источника 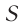до приемника 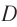, т. е. появится дополнительная «разность хода» интерферирующих световых волн.

При повороте платформы на 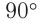лучи «менялись местами» и соответственно должна была измениться разность хода. Как показывали расчеты, это привело бы к смещению интерференционной картины на 0,4 ширины интерференционной полосы. Однако ожидаемое смещение не было обнаружено, хотя интерферометр Майкельсона позволял наблюдать сдвиг интерференционной картины даже на 0,01 полосы.

Эксперименты повторялись в разное время суток и в разные времена года (т. е. при различных направлениях скорости интерферометра относительно эфира). Во всех случаях смещение отсутствовало. Это было настолько же невероятно, как если при езде на мотоцикле вы не почувствовали бы встречного воздушного потока.

Результаты опыта Майкельсона — Морли и многих других экспериментов по измерению скорости света привели к выводу о независимости скорости света в вакууме как от движения приемника, так и от движения источника излучения. Представления о существовании мирового эфира оказались несостоятельными.

Данный факт был одной из величайших загадок физики конца XIX — начала XX в. Обнаружилось явное противоречие между экспериментом и классическими представлениями. Так, при переходе от одной ИСО к другой, согласно классическому закону сложения скоростей, к скорости света должна векторно прибавляться скорость движения этих ИСО друг относительно друга. Однако эксперимент упрямо утверждал, что скорость света в вакууме постоянна и во всех ИСО одинакова.

Это был вызов механической картине мира, которая складывалась веками.

Выдающиеся ученые того времени (А. Пуанкаре, Г. А. Лоренц и др.) выдвинули целый ряд полезных идей для объяснения этого противоречия. Однако решающий шаг был сделан в 1905 г. 25-летним физиком Альбертом Эйнштейном, работавшим тогда техническим экспертом Федерального патентного бюро в Берне (Швейцария). Им была создана новая теория пространства и времени, получившая название специальная теория относительности. Эта революционная теория позволила не только объяснить результат опыта Майкельсона — Морли, но и положила начало новому этапу развития физики.

Постулаты специальной теории относительности

Фундаментальное утверждение, лежащее в основе теории и принимаемое без доказательства, называется постулатом (аксиомой). В физике постулат, как правило, является обобщением экспериментальных фактов.

Как отмечалось в предыдущем параграфе, физика столкнулась с противоречием между постоянством скорости света в вакууме и классическим законом сложения скоростей. Проиллюстрируем эту проблему на простом примере: автомобиль движется со скоростью 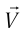 навстречу лучу прожектора. Согласно классическому закону сложения скоростей в системе отсчета «автомобиль» скорость света должна быть равной 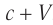. Однако результаты экспериментов свидетельствуют: во всех  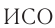скорость света в вакууме равна .

Для преодоления указанного противоречия пришлось глубоко проанализировать и пересмотреть классические представления о пространстве и времени, в результате чего была создана специальная теория относительности.

В основу данной теории Эйнштейн положил два постулата, являющихся обобщением экспериментальных фактов.

Первый постулат (постулат относительности):

• во всех инерциальных системах отсчета все физические явления при одинаковых начальных условиях происходят одинаковым образом.

Данный постулат представляет собой обобщение механического принципа относительности на все физические явления. Он говорит о том, что никакими экспериментами, проведенными внутри ИСО, невозможно установить, покоится она или движется.

Представим себе вагон, движущийся равномерно и прямолинейно без толчков и покачиваний. Можно ли установить факт движения вагона с помощью экспериментов (механических, электромагнитных и любых других), проводимых внутри него? Весь накопленный в физике опыт показывает, что это невозможно в полном соответствии с первым постулатом .

Второй постулат (постулат постоянства скорости света):

• во всех инерциальных системах отсчета скорость света в вакууме одинакова и не зависит ни от скорости источника, ни от скорости приемника излучения.

Как уже говорилось, этот постулат полностью соответствует результатам многократно проводившихся экспериментов, но противоречит классическому закону сложения скоростей.

Эйнштейн разрешил это противоречие, проведя глубокий анализ представлений о времени и пространстве.

В основе этого анализа лежит понятие событие. Под событием понимают некоторое явление, происходящее в определенной точке пространства в определенный момент времени. Понятие «событие» является идеализацией реального явления, происходящего очень быстро в очень малой области пространства. Примером события может служить вспышка света, выстрел орудия, соударение двух частиц, пересечение спортсменом линии финиша и т. д. Для характеристики времени и места события в определенной 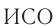 достаточно указать три его координаты и момент времени.

События, произошедшие в один и тот же момент времени, называются одновременными. В классической физике принималось положение об абсолютности одновременности: если два события произошли одновременно в некоторой 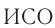, то они одновременны и в любой другой .

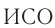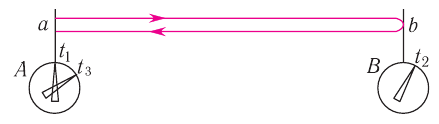
Рис. 101. Синхронизация часов

Эйнштейн обратил внимание на то, что абсолютность одновременности вовсе не очевидна. Для решения вопроса об одновременности (или неодновременности) двух событий, происходящих в разных местах некоторой 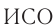, необходимо в каждом месте иметь часы, покоящиеся относительно этой  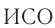и синхронизованные между собой. Только тогда можно решать вопрос об одновременности событий относительно данной .

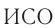Процедура синхронизации должна опираться на надежно проверенные физические законы. Эйнштейн предложил следующий способ. Пусть в точке 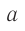находятся часы 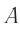, а в точке 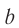— часы 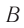(рис. 101). Световой сигнал идет из точки 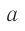в точку 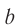, мгновенно отражается в этой точке и возвращается в точку 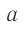. Поскольку скорость света постоянна, то часы 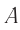и часы 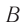следует считать идущими синхронно, если выполняется равенство:

где 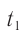 — показания часов  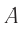в момент старта сигнала из точки 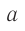, 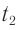— показания часов  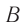в момент прихода сигнала в точку 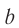,  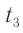— показания часов 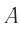в момент возвращения сигнала в точку 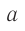. Используя условие (1), можно провести синхронизацию для любой пары часов, покоящихся в некоторой 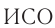. Ход такой совокупности синхронизованных часов и есть ход времени в данной .

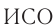Теперь можно приступить к проверке абсолютности (или относительности) одновременности. Рассмотрим мысленный эксперимент с вагоном и двумя наблюдателями, один из которых 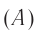стоит на платформе, а второй 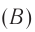находится в вагоне (рис. 102).

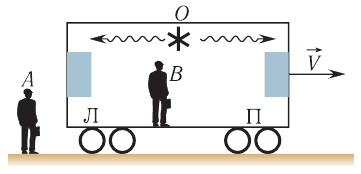
Рис. 102. Относительность одновременности

Пусть в центре вагона, в точке 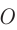 , расположен источник света (см. рис. 102), а правая и левая стенки вагона оборудованы фотоэлементами 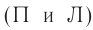, позволяющими определять момент прихода светового сигнала. Понятно, что если световая вспышка произойдет в середине неподвижного вагона, то световой сигнал будет зарегистрирован фотоэлементами П и Л одновременно как по часам, находящимся в вагоне, так и по часам 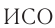, связанной с платформой.

Пусть теперь вагон движется относительно платформы вправо равномерно и прямолинейно (см. рис. 102) со скоростью 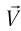. С точки зрения наблюдателя 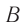, для которого вагон по-прежнему покоится, световые сигналы от вспышки в точке 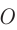достигнут фотоэлементов П и Л одновременно.

Иную картину видит наблюдатель 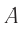. Относительно него вагон движется. В результате этого правая стенка вагона удаляется от того места, где произошла вспышка, а левая — приближается к нему. Значит, относительно платформы свету придется пройти от места вспышки 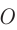до фотоэлемента Л меньший путь, чем от 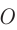до фотоэлемента П. При этом согласно второму постулату скорость света относительно платформы равна с и для сигнала, движущегося вправо, и для сигнала, движущегося влево. В итоге свет сначала достигнет фотоэлемента Л и только потом — фотоэлемента П. Для наблюдателя 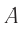эти события неодновременны.

Кто же из наблюдателей прав? Правы оба. События, одновременные в одной ИСО, могут оказаться не одновременными в другой , движущейся относительно первой.

Таким образом, одновременность событий — понятие относительное. Отметим однако, что одновременные события, произошедшие в одном и том же месте, одновременны в любой . Их одновременность абсолютна.

Пространство и время в специальной теории относительности

Установление того факта, что одновременность относительна, заставило по-новому взглянуть на свойства пространства и времени. Как изменяются свойства пространства и времени при скоростях, близких к скорости света? Где и как это необходимо учитывать?

Рассмотрим два эффекта : эффект замедления времени и эффект сокращения длины.

Эффект замедления времени

Кажется очевидным, что промежуток времени между двумя событиями не зависит от того, измерен он движущимися или покоящимися часами. Пусть, например, участник автогонки измерил по часам, находящимся в его автомобиле, промежуток времени от старта до финиша. Он не сомневается, что результат будет таким же и у судейской бригады. А отличаются ли эти результаты на самом деле?

Рассмотрим простой мысленный эксперимент. Закрепим лампу  и зеркало 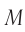на противоположных концах жесткого стержня длиной 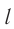(рис. 103). Лампа 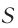дает кратковременную вспышку (событие 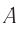). Свет отражается от зеркала 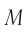и возвращается обратно (событие 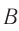) (см. рис. 103, а). Пусть стержень движется вправо с постоянной скоростью 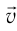, перпендикулярной стержню (см. рис. 103, б).

В системе отсчета 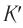, движущейся вместе со стержнем (в его «собственной» 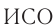, см. рис. 103, б) события 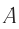и 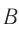происходят в одном и том же месте. Промежуток времени 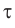между этими событиями, измеренный часами системы 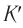, называют промежутком собственного времени. Очевидно, что .

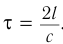Найдем теперь промежуток времени 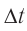 между этими же событиями по часам системы 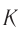, относительно которой стержень движется («лабораторной» ИСО). Величину 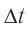называют промежутком лабораторного времени.

С точки зрения лабораторной системы 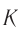события 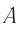и 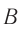происходят в разных местах (см. рис. 103, б). Согласно этому рисунку за время 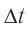свет проходит путь 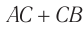, равный

Относительно системы 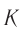стержень движется со скоростью 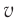, а свет — со скоростью 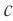. Поэтому 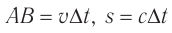и равенство (1) примет вид

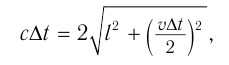 откуда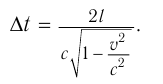 

Сравнивая 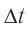и 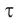, получим:

Соотношение (2) показывает, что промежуток собственного времени 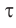между двумя событиями всегда меньше, чем промежуток времени 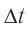между этими же событиями по часам лабораторной 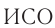. Этот эффект называют релятивистским замедлением времени.

Связь (2) между собственным и лабораторным временем записывают также в виде 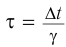, где коэффициент 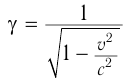называется лоренцевым множителем. При всех значениях скорости  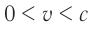множитель .

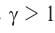Релятивистское замедление времени состоит в том, что собственное время в 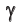раз меньше, чем лабораторное.

Как определяются понятия собственного и лабораторного времени в общем случае?

Собственным временем 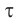называется промежуток времени между двумя событиями, измеренный часами той ИСО, относительно которой эти события произошли в одном и том же месте. Собственное время можно всегда измерить одними часами.

Промежуток времени, измеренный часами , относительно которой события произошли в разных местах, мы называем лабораторным временем. Для его измерения необходимо как минимум двое часов, синхронизованных между собой.

Вернемся к примеру с автогонками. Промежуток времени от старта до финиша, измеренный по часам в автомобиле, является собственным временем, а промежуток времени между этими событиями, измеренный по часам судейской бригады, — лабораторным. Значит, судьи зафиксируют время, в у раз большее, чем автогонщик. Подсчитайте, существенно ли это различие для автогонок (скорость автомобиля и длину трассы задайте самостоятельно) и для «гонок» протонов, выброшенных Солнцем во время вспышки и движущихся со скоростью 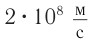 по трассе «Солнце — Земля».

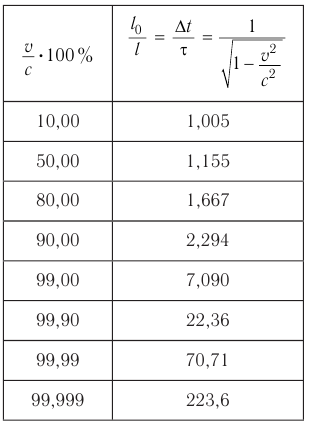
Количественные оценки релятивистского замедления времени даны в таблице 7 (с. 145).

Эффект замедления времени — это его объективное свойство. При релятивистских скоростях эффект может быть очень существенным. Отметим однако, что на воображаемом космическом корабле, движущемся с релятивистской скоростью, находящиеся в нем люди не почувствуют замедления жизненного ритма. Дело в том, что все происходящие в движущейся 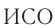 процессы (физические, химические, биологические) будут замедляться в одной и той же мере — все они будут идти в соответствии с ходом собственного времени этой .

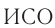Из-за эффекта релятивистского замедления времени, ход часов на орбитальных спутниках отличается от земного на несколько десятков микросекунд за сутки. Это отличие учитывается в спутниковых системах навигации. Без такого учета они не обеспечивали бы необходимой точности позиционирования объектов.

Эффект сокращения длины

Пусть вагон 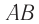движется относительно платформы с постоянной скоростью  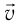(рис. 104). Чему равна длина движущегося вагона с точки зрения инерциальной системы отсчета, связанной с платформой?

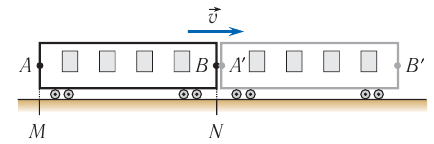
Рис. 104. Сокращение длины

Не останавливая вагон, нанесем на платформу метки и (см. рис. 104) так, чтобы метка 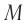находилась под точкой  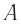вагона, а метка 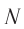— под точкой 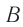в один и тот же момент времени по часам платформы. Длину движущегося вагона в системе отсчета «платформа» определим как расстояние 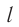между этими метками 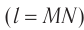. Согласно обычным представлениям при любой скорости длина 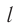 и собственная длина вагона  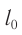(т. е. длина вагона в той системе отсчета, в которой он покоится) равны между собой.

Релятивистская теория утверждает, что это не так. Согласно СТО величины 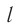и 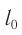связаны соотношением:

С точки зрения неподвижного наблюдателя движущееся тело сокращается в направлении своего движения в 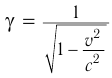раз.

Это явление называется лоренцевым (или релятивистским) сокращением длины. Заметим, что при этом поперечные размеры тела (т. е. измеренные вдоль осей, перпендикулярных направлению движения) не изменяются. Постоянство поперечных размеров мы использовали при выводе формулы (2).

Для оценки эффекта лоренцева сокращения можно воспользоваться таблицей 7. Из нее видно, что при расчетах с точностью 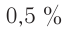для скоростей 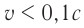нет необходимости применять релятивистские формулы.

Таблица 7. Сокращение длины и замедление времени

Выведем соотношение (3). Представим, что при прохождении точки вагона над меткой 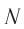(см. рис. 104) происходит кратковременная вспышка красного цвета (событие 1), а затем при прохождении точки 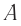над меткой 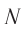— синего цвета (событие 2). С точки зрения  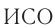«платформа» эти события произошли в одном и том же месте — там, где нанесена метка 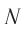. Значит, время, прошедшее между красной и синей вспышкой в этой 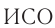, является промежутком собственного времени 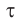. Его можно измерить одними часами, находящимися на платформе возле метки 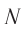(см. рис. 104).

С точки зрения 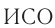 «вагон» события 1 и 2 произошли в разных местах: красная вспышка — в точке 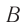вагона, синяя — в точке 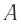. Время, прошедшее между этими событиями в  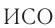«вагон», является промежутком лабораторного времени 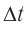. Согласно формуле (2)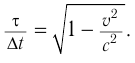 

Относительно ИСО «платформа» точка 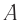вагона за время 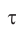прошла путь 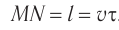. Относительно  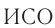«вагон» метка 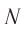за время 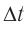— путь 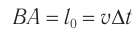. Таким образом,  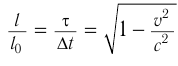, что и требовалось доказать.

Пример решения задачи №1

Определите модуль скорости 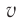 с которой должен двигаться космический корабль, если с точки зрения наблюдателя на Земле ход времени на нем замедлился в 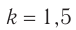. Скорость распространения света в вакууме .

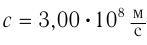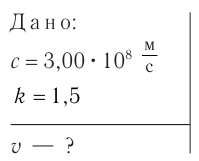
Решение

Из формулы замедления времени:

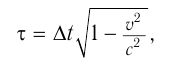
где 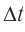— промежуток времени, измеренный на Земле, 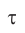— соответствующий ему промежуток времени, измеренный на корабле. Получим:

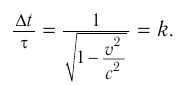
Из этого выражения находим модуль скорости движения корабля:

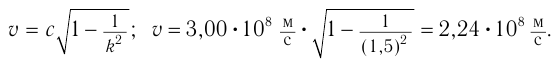
Ответ: .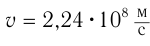

Преобразования Галилея и преобразования Лоренца

Пусть в начальный момент времени оси координат двух инерциальных систем отсчета 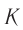и 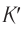совпадают, а система 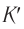движется относительно 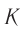со скоростью 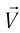, направленной вдоль оси 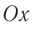(рис. 105). Пусть с точки зрения системы 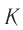некоторое событие произошло в момент времени 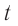в точке с координатами 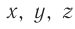. Чему равны координаты 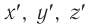и момент времени 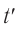этого события в системе ?

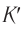В рамках классических представлений о пространстве и времени ответ очевиден:

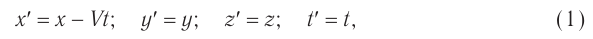
где 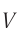— модуль скорости движения системы 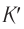относительно системы .

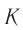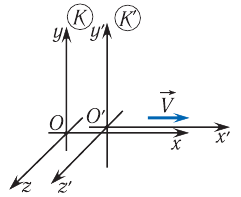
Рис. 105. Движение ИСО  относительно

Соотношения (1) называются преобразованиями Галилея. Они отражают абсолютность времени в классической механике 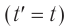 и соответствуют классическим представлениям о неизменности размеров тел при переходе от одной  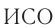к другой.

Ясно, что преобразования Галилея противоречат 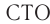, в которой и время, и длина могут измениться при переходе от одной  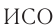к другой. При учете эффектов релятивистского замедления времени и сокращения длины вместо преобразований Галилея (1) получатся соотношения:

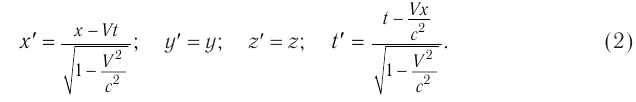
Они были найдены нидерландским физиком Хендриком Лоренцом и называются преобразованиями Лоренца. Отметим, что при малых скоростях (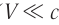) преобразования Лоренца переходят в преобразования Галилея, справедливые в классической механике. К этому выводу легко прийти, сравнив формулы (1) и (2).

С помощью преобразований Лоренца можно получить релятивистский закон сложения скоростей. Приведем без вывода формулу, выражающую этот закон для простого частного случая. Пусть некоторый объект (тело, частица, световой импульс и т. д.) движется относительно системы со скоростью навстречу системе 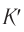(так что векторы 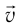и 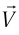имеют противоположные направления). Тогда, согласно , модуль скорости этого объекта относительно системы 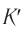будет равен:

По формуле (3) легко найти, что световой импульс, для которого 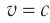, будет иметь относительно 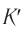скорость

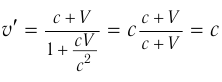
при любом возможном значении 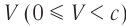. Легко проверить также, что, даже если и скорость 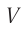системы 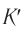, и скорость 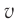движущегося навстречу ей тела близки к скорости света 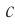, по формуле (3) получится: 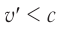. Значит, релятивистский закон сложения скоростей находится в полном согласии с утверждением, что скорость света  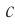в вакууме является предельной скоростью движения материальных объектов и распространения сигналов.

Заметим, что при 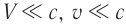релятивистская формула (3) переходит в соотношение 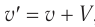, вытекающее из закона сложения скоростей Галилея.

Элементы релятивистской динамики. Взаимосвязь массы и энергии

Изменение представлений о свойствах пространства и времени привело к обнаружению тесной взаимосвязи между массой и энергией и к изменению законов динамики. Чем законы релятивистской динамики отличаются от законов динамики Ньютона?

Необходимость изменения динамики очевидна хотя бы из того, что, согласно законам Ньютона, любое тело можно в принципе разогнать до любой скорости. Приложим к покоящемуся телу массой 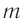 постоянную силу 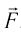. Используя второй закон Ньютона, найдем, что к моменту времени 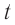тело развивает скорость 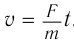. Следовательно, в рамках классической механики при 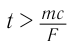скорость тела 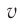превзошла бы скорость света 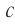, что противоречит результатам экспериментов и основным положениям .

Какие же соотношения динамики изменились при переходе к , а какие — остались неизменными?

Сохранили свой вид законы изменения импульса и энергии тела:

где 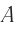— работа, совершенная силой 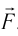. Изменились соотношения, выражающие зависимость импульса и энергии тела от его скорости:

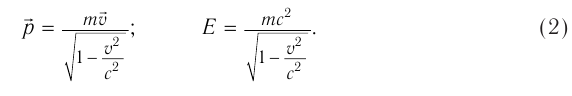
Решим задачу о движении тела под действием постоянной силы по законам динамики . Если при тело покоилось, то, согласно первому из соотношений (1), в момент времени модуль импульса частицы будет равен 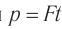(как и в механике Ньютона). Но если в ньютоновой механике из 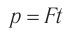следует и  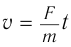скорость  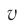с течением времени неограниченно растет, то в релятивистском случае с учетом (2) получается:

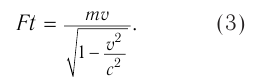
Выразив 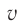из формулы (3), находим:

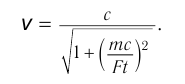
График зависимости 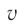от 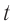(рис. 106) показывает, что скорость тела никогда не достигнет предельного значения .

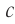С помощью формулы (3) легко найти промежуток времени 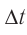, необходимый для увеличения скорости частицы от  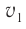 до :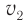

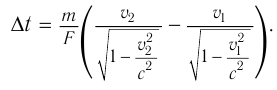
Численные расчеты поданной формуле при 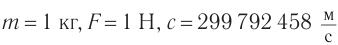 показывают: разгон тела от 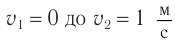,  как и от  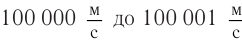 произойдет практически за одну секунду, как и по законам Ньютона. Разгон от 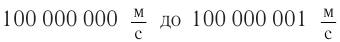займет 1,2 с. Однако чтобы добавить еще 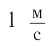к скорости 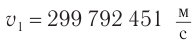, тело пришлось бы разгонять более чем три тысячи лет!

О чем говорит этот пример? О том, что инертность тела неограниченно возрастает по мере приближения скорости тела к скорости света .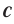

При этом масса 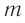в  для каждого тела остается постоянной величиной, характеризующей его инертность. Как и в нерелятивистской механике, числовое значение массы показывает, насколько данное тело инертнее, чем тело, принятое за эталон массы.

Согласно соотношениям (2) при скорости 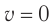 энергия тела равна величине

называемой энергией покоя. Таким образом, согласно 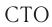, масса тела является мерой его энергии в состоянии покоя. Это свойство массы было неизвестно в классической механике. В каждом теле таится огромный запас энергии. Например, тело массой 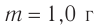обладает энергией покоя

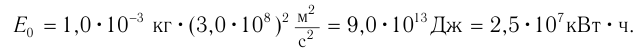
Она эквивалентна энергии, выделяющейся при сгорании 2000 т нефти. Так, благодаря прогрессу физики в 1905 г. человечество узнало о практически неисчерпаемых запасах энергии, содержащихся в любом веществе.

Из равенства (4) следует, что изменение энергии покоя тела на 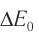 вызывает изменение его массы на 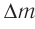, где

Утверждение о том, что энергия покоя пропорциональна массе, а изменение энергии покоя вызывает изменение массы, называют законом взаимосвязи массы и энергии. Математическим выражением этого закона служат формулы (4) и (5).

Формула (5) применима ко всем явлениям, в которых изменяется внутренняя энергия вещества. При процессах, происходящих на атомно-молекулярном уровне, изменения массы крайне малы. Так, при полном превращении льда в воду относительное изменение массы 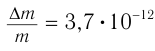, при нагревании на  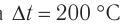железного бруска 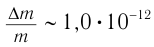. При химических реакциях относительное изменение массы несколько выше. Например, при сгорании метана в кислороде 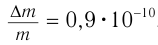. Для ядерных реакций ситуация существенно иная. Для них характерны величины 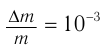, в десятки миллионов раз большие, чем для химических реакций.

В формуле (2) энергия 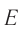 движущегося тела включает его энергию покоя 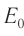. Кинетическая энергия 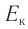в 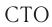 определяется как разность :

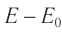Если соответствие между релятивистским импульсом и классическим импульсом при 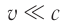очевидно, то для кинетической энергии оно требует доказательства. Введем обозначение

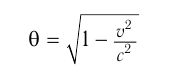
и проделаем простые преобразования:

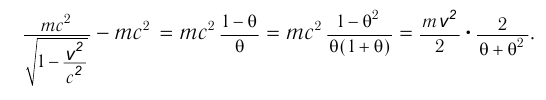
Множитель 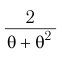   при малых скоростях практически равен единице. Следовательно, при кинетическая энергия (6), как и должно быть, переходит в нерелятивистское выражение .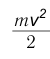

Исключая скорость 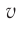из формул (2), можно получить соотношение:

Формула (7) позволяет с большой точностью определить массу частицы по результатам измерений ее энергии и импульса. Такой метод широко используется в физике элементарных частиц.

В начале параграфа было показано, что согласно 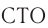частица не может достичь скорости света. Данный запрет не распространяется на частицы, масса которых 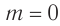. Такие безмассовые частицы находятся всегда в состоянии движения со скоростью 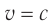. Энергия безмассовой частицы в соответствии с релятивистским соотношением (7) пропорциональна ее импульсу: .

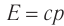Согласно принципу соответствия любая новая физическая теория, претендующая на более глубокое описание физических явлений, должна включать в себя классическую (ньютоновскую) теорию как предельный случай.

Специальная теория относительности полностью удовлетворяет принципу соответствия. При скоростях  ее законы переходят в законы классической механики.

Пример решения задачи №2

Солнце ежесекундно излучает в пространство 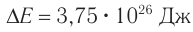энергии. На сколько уменьшается ежесекундно масса 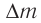Солнца вследствие излучения? На сколько лет 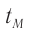«хватит» Солнца при таком расходе массы, если масса Солнца ?

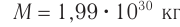Решение

Из закона взаимосвязи массы и энергии находим:

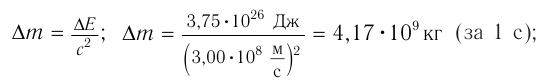
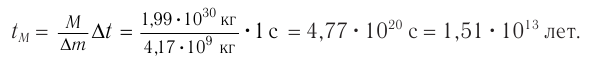
Ответ: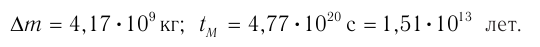

Основные формулы и законы

Постулаты специальной теории относительности

Постулат относительности: во всех инерциальных системах отсчета все физические явления при одинаковых начальных условиях происходят одинаковым образом.

Постулат постоянства скорости света: во всех инерциальных системах отсчета скорость света в вакууме одинакова и не зависит ни от скорости источника, ни от скорости приемника излучения.

Предельная скорость

Скорость света в вакууме является предельной скоростью движения материальных объектов и распространения сигналов.

Релятивистское замедление времени

Промежуток собственного времени 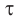 между двумя событиями, измеренный движущимися часами 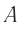, меньше, чем промежуток времени  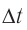между этими же событиями, прошедший в инерциальной системе отсчета, относительно которой часы А двигались:

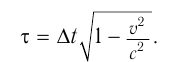
Релятивистское сокращение длины

Линейный размер движущегося тела сокращается в направлении его движения: 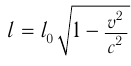, где 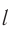— длина тела в инерциальной системе отсчета, относительно которой оно движется, а 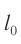— длина тела в инерциальной системе отсчета, в которой оно покоится. Поперечные размеры тела при движении не изменяются.

Энергия и импульс тела

Энергия, импульс тела и его инертность неограниченно растут при приближении скорости тела к предельной скорости .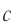

Взаимосвязь энергии и массы

Энергия покоя 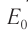 тела пропорциональна его массе:

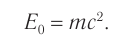
Изменения массы и энергии покоя взаимосвязаны:

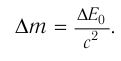
Что такое принцип относительности Галилея

Рассматривая движение тел в разных инерциальных СО, Г. Галилей пришел к выводу, который называют принципом относительности Галилея:

Во всех инерциальных системах отсчета течение механических явлений и процессов происходит одинаково при одинаковых начальных условиях.

Галилей писал: «Если мы, находясь в каюте парусника, будем проводить какие-либо эксперименты, то ни сами эксперименты, ни их результаты не будут отличаться от тех, которые проводились бы на берегу. И только поднявшись на палубу, мы увидим: оказывается, наш корабль движется равномерно прямолинейно...».

Выводы:

• Закон инерции: тело движется равномерно прямолинейно или находится в состоянии покоя, если на него не действуют другие тела или их действия скомпенсированы.
• Первый закон Ньютона: существуют такие системы отсчета, относительно которых тело сохраняет состояние покоя или равномерного прямолинейного движения, если на него не действуют никакие силы или если эти силы скомпенсированы. Такие СО называют инерциальными.
• В качестве инерциальных обычно используют СО, связанные с Землей. Любая СО, движущаяся относительно инерциальной СО равномерно прямолинейно, тоже является инерциальной. Во всех инерциальных СО течение механических явлений и процессов одинаково при одинаковых начальных условиях.

Сила. Масса. Второй и третий законы ньютона

Представьте: вы разогнались на велосипеде и перестали крутить педали. В конце концов велосипед обязательно остановится — его скорость постепенно упадет до нуля. А вот время остановки велосипеда, а следовательно, и его ускорение существенно зависят от того, нажимаете ли вы при этом на тормоз. То есть одно и то же тело в результате разного воздействия (взаимодействия) получает разное ускорение. В результате разного воздействия тело может также по-разному изменять свои форму и размеры — деформироваться.

Количественной мерой взаимодействия является сила.

Сила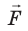 в механике — это векторная физическая величина, являющаяся мерой взаимодействия тел, в результате которого тела получают ускорения или (и) деформируются.

Единица силы в СИ — ньютон: [F] =1 Н (N). 1 Н равен силе, которая, действуя на тело массой 1 кг, сообщает ему ускорение 1 м/с2.

Силой называют также действие одного тела на другое. Например, можно сказать: на мяч действует сила упругости, хотя на самом деле на мяч действуют руки волейболиста, действие которых характеризует сила упругости. Результат действия силы 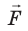зависит от модуля F этой силы, ее направления и места приложения (если тело не является материальной точкой) (рис. 10.1).

Рис. 10.1. Если вы, играя в волейбол, ударите по мячу, то можете ускорить его движение, остановить, изменить направление движения или закрутить — это зависит от направления, точки приложения и силы удара

Почему тела по-разному реагируют на одно и то же действие

Изменение скорости движения тела зависит не только от силы, действующей на тело: если к теннисному мячу и метательному ядру приложить одинаковую силу, скорость движения ядра изменится меньше или для того же изменения скорости необходимо будет больше времени. То есть разным телам свойственно по-разному реагировать на одно и то же действие.

Свойство тела, которое заключается в том, что для изменения скорости движения тела под действием силы требуется некоторое время, называют инертностью.

Чем тело инертнее, тем меньшее ускорение оно приобретает в результате одного и того же действия. В приведенном выше примере ядро инертнее мяча, ведь в результате одного и того же действия оно медленнее мяча изменяет скорость своего движения. Инертные свойства тела характеризует инертная масса тела.

Любое тело имеет также свойство гравитационно взаимодействовать с другими телами. Это свойство характеризуется гравитационной массой тела. Инертная масса тела равна его гравитационной массе, поэтому далее будем говорить просто о массе тела.

Масса m — физическая величина, являющаяся мерой инертности и мерой гравитации тела. Единица массы в СИ — килограмм: [m ] =1 кг (kg).

Измерить массу тела означает сравнить ее с массой тела, масса которого принята за единицу. Один из распространенных способов прямого измерения массы тела — взвешивание (масса — мера гравитации, поэтому тела равной массы одинаково притягиваются к Земле, а значит, одинаково давят на опору).

Взвешивание — самый удобный способ измерения массы, но не универсальный. Как, например, измерить массу молекулы или массу Луны, ведь положить эти объекты на весы невозможно? В таких случаях используют тот факт, что масса — мера инертности. Если на два тела массами 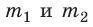действуют одинаковые силы, то сравнить массы этих тел можно, если определить ускорения, приобретенные телами в результате действия этих сил:

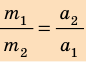
Основные свойства массы:

1. Масса тела — величина инвариантная: она не зависит ни от выбора системы отсчета, ни от скорости движения тела.
2. В классической механике масса тела — величина аддитивная: масса тела равна сумме масс всех частиц, из которых состоит тело, а масса системы тел равна сумме масс тел, образующих систему.
3. В классической механике выполняется закон сохранения массы: при любых процессах в системе тел общая масса системы остается неизменной; масса тела не изменяется при его взаимодействии с другими телами.