
Принцип Гюйгенса — Френеля в физике - формулы и определения с примерами
Принцип Гюйгенса — Френеля:
Среда называется однородной, если ее физические свойства по всему объему одинаковы во всех точках пространства. Среда называется изотропной, если ее физические свойства одинаковы по всем направлениям в пространстве.
Волновой фронт — это поверхность, все точки которой колеблются в одинаковых фазах, т. е. это поверхность равных фаз.
Волна называется плоской, если ее волновой фронт является плоскостью.
Закономерности распространения волн любой природы в различных средах носят универсальный характер.
Для наглядности рассмотрим процесс распространения волн на поверхности воды. Волны, возбуждаемые точечным источником 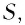
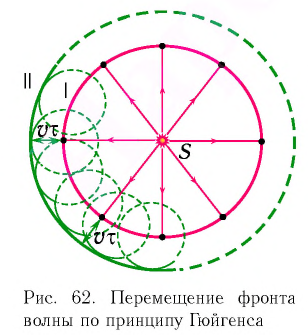
Общие закономерности процесса распространения волн объяснил Христиан Гюйгенс, сформулировав в 1690 г. в «Трактате о свете» принцип, позволяющий определять положение волнового фронта через небольшой промежуток времени, зная Рис. 62. Перемещение фронта его положение в данный момент времени. Согласно волны по принципу Гюйгенса принципу Гюйгенса: каждая точка среды, которой волновой фронт достиг в момент времени 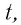 становится источником вторичных сферических волн. Новое положение волнового фронта через малый промежуток времени
становится источником вторичных сферических волн. Новое положение волнового фронта через малый промежуток времени 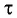 определяется огибающей волновых фронтов вторичных волн в момент времени
определяется огибающей волновых фронтов вторичных волн в момент времени 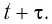
Таким образом, согласно принципу Гюйгенса для нахождения положения волнового фронта через промежуток времени 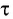 проведем окружности радиусом
проведем окружности радиусом 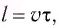 представляющие собой фронты вторичных волн с центрами на фронте в положении I (см. рис. 62). Соответственно, огибающая волновых фронтов вторичных волн определяет новое положение волнового фронта — положение II. Напомним, что огибающей называется поверхность, касательная ко всем вторичным волнам. На очень больших расстояниях от точечного источника излучаемые им волны можно считать плоскими.
представляющие собой фронты вторичных волн с центрами на фронте в положении I (см. рис. 62). Соответственно, огибающая волновых фронтов вторичных волн определяет новое положение волнового фронта — положение II. Напомним, что огибающей называется поверхность, касательная ко всем вторичным волнам. На очень больших расстояниях от точечного источника излучаемые им волны можно считать плоскими.
Линия, перпендикулярная волновому фронту в данной точке, называется лучом. Луч определяет направление распространения волны, а также направление переноса энергии волной. Например, в солнечном излучении, приходящем на Землю, световые лучи являются практически параллельными друг другу.
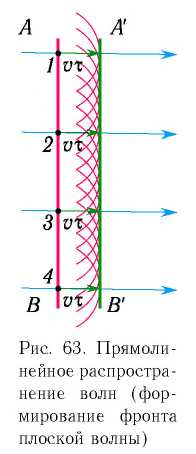
Принцип Гюйгенса объясняет прямолинейное распространение волн в однородной среде. Поскольку в такой среде радиусы фронтов вторичных волн 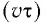 одинаковы на всех участках (рис. 63), то волновой фронт
одинаковы на всех участках (рис. 63), то волновой фронт 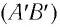 плоской волны с течением времени перемещается в одном и том же направлении, оставаясь параллельным своему начальному положению
плоской волны с течением времени перемещается в одном и том же направлении, оставаясь параллельным своему начальному положению 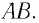
Однако от закона прямолинейного распространения света наблюдаются отклонения при его распространении вблизи границ непрозрачных тел или прохождении через отверстия в непрозрачных экранах, т. е. в средах с резко выраженными неоднородностями. Причем отклонение существенно зависит от соотношения между длиной волны и размером препятствия. Действительно, стоя за углом дома, мы хорошо слышим, что едет автомобиль, хотя не видим его, поскольку находимся в области «тени». Таким образом, звуковые волны как бы «заворачивают за угол», в то время как световым волнам этого сделать не удается.
Явление огибания волнами препятствий, которое проявляется в отклонении направления распространения волн от
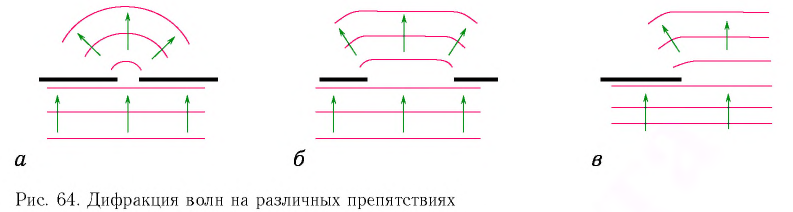
прямолинейного, называется дифракцией (рис. 64). Явление дифракции служит одним из подтверждений волновой природы света.
Для проявления дифракции размеры препятствий (отверстий) должны быть меньше или сравнимы с длиной волны, вот почему в рассмотренном примере звук 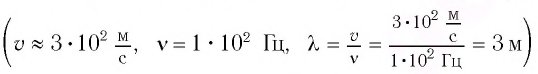 мотора автомобиля смог «завернуть за угол», а свет
мотора автомобиля смог «завернуть за угол», а свет 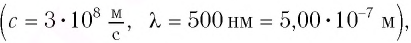 отраженный от автомобиля, — нет.
отраженный от автомобиля, — нет.
Принцип Гюйгенса позволяет решать задачи лишь о направлении распространения волнового фронта и не затрагивает вопрос об амплитуде, а следовательно, и об интенсивности распространяющихся по разным направлениям волн.
Изучая дифракцию света, французский физик Огюстен Жан Френель дополнил принцип Гюйгенса представлением об интерференции вторичных волн, которые являются когерентными. Принцип Гюйгенса — Френеля позволил описать явление дифракции количественно:
все источники вторичных волн, расположенные на волновом фронте, когерентны между собой. Для расчета амплитуды огибающей волны в данной точке пространства следует учесть интерференцию вторичных волн от всех участков волнового фронта в начальном положении.
Таким образом, согласно Френелю дифракция света объясняется интерференцией вторичных волн от различных участков начального положения волнового фронта.
Для наблюдения дифракции света используется дифракционная решетка.
Дифракционной решеткой называют оптический прибор, предназначенный для точного измерения длин волн и анализа состава света.
Дифракционная решетка состоит из большого числа равноотстоящих параллельных штрихов (щелей), нанесенных на стеклянную или металлическую поверхность. Длина решеток составляет 10— 15 см. Они содержат 10 000—20 000 штрихов на 1 см. Наблюдения проводятся как в отраженном свете (на металлических решетках), так и в проходящем свете (на стеклянных).
Рассмотрим дифракционную решетку, представляюшую собой систему из 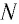 одинаковых равноотстоящих параллельных щелей (прозрачные участки)в плоском непрозрачном экране (рис. 65). Если ширина каждой щели
одинаковых равноотстоящих параллельных щелей (прозрачные участки)в плоском непрозрачном экране (рис. 65). Если ширина каждой щели 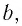 ширина непрозрачной части между щелями
ширина непрозрачной части между щелями 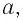 то величина
то величина 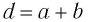 называется постоянной решетки или ее периодом.
называется постоянной решетки или ее периодом.
Пусть на решетку, постоянная которой равна 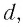 падает плоская волна, длина которой
падает плоская волна, длина которой 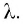 Из принципа Гюйгенса следует, что волны, дифрагировавшие на щелях, распространяются за решеткой по всем направлениям (рис. 66).
Из принципа Гюйгенса следует, что волны, дифрагировавшие на щелях, распространяются за решеткой по всем направлениям (рис. 66).
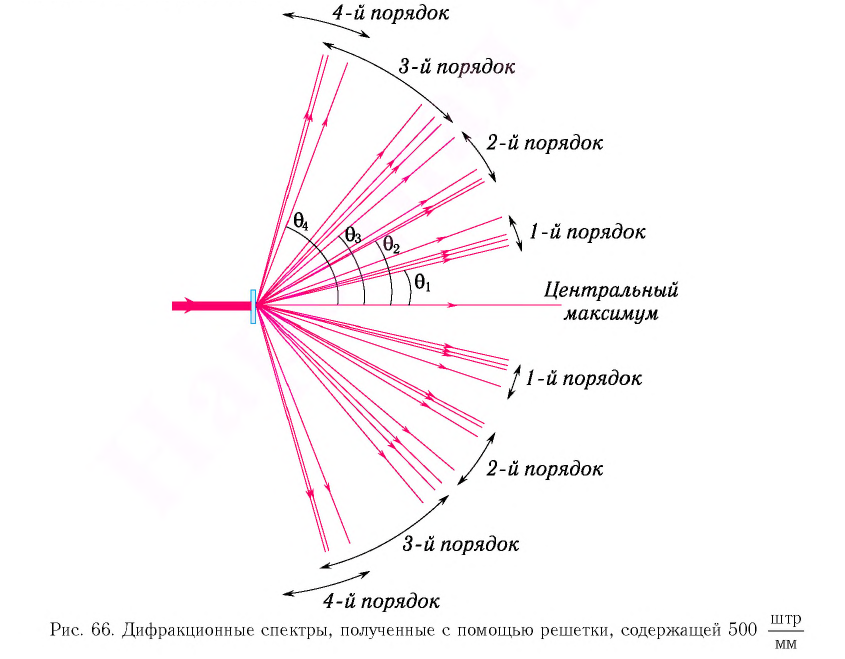
Для наблюдения дифракционной картины на экране между ним и решеткой размещают собирающую линзу таким образом, чтобы экран находился в фокальной плоскости линзы (см. рис. 65). Собирающая линза фокусирует на экране падающие на нее параллельные лучи (вторичные волны).
В зависимости от разности хода между вторичными волнами, испущенными разными щелями, они интерферируют друг с другом, усиливая или ослабляя друг друга. На экране получается дифракционная картина в виде системы светлых и темных полос.
Наиболее яркие дифракционные максимумы получили название главных дифракционных максимумов.
Условие возникновения главных дифракционных максимумов, наблюдаемых под углами 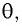 имеет вид:
имеет вид:
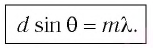
Здесь 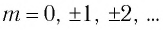 — порядок максимума, или порядок спектра,
— порядок максимума, или порядок спектра, 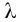 — длина волны падающего излучения.
— длина волны падающего излучения.
Полученное условие определяет направления распространения света в пространстве, по которым на отрезке 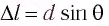 укладывается целое число длин волн
укладывается целое число длин волн 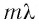 (см. рис. 65).
(см. рис. 65).
Следовательно, вторичные волны от всех щелей решетки приходят в точку наблюдения синфазно (с фазами, отличающимися на число, кратное 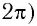 и усиливают друг друга.
и усиливают друг друга.
Между максимумами интенсивности расположены минимумы, так как при изменении угла 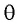 на отрезке
на отрезке 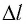 уже не будет укладываться целое число длин волн.
уже не будет укладываться целое число длин волн.
Следовательно, вторичные волны приходят в точку наблюдения, ослабляя результирующее действие.
Из условия возникновения главных дифракционных максимумов (1) следует, что при 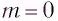 для любых длин волн
для любых длин волн 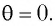 Следовательно, прямо по центру решетки образуется нулевой максимум, который называется также центральным максимумом. Дифракционные максимумы, соответствующие
Следовательно, прямо по центру решетки образуется нулевой максимум, который называется также центральным максимумом. Дифракционные максимумы, соответствующие 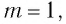 образуют спектр первого порядка,
образуют спектр первого порядка, 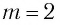 — спектр второго порядка и т. д. (см. рис. 66).
— спектр второго порядка и т. д. (см. рис. 66).
Количество максимумов 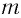 в дифракционной картине ограничено, поскольку
в дифракционной картине ограничено, поскольку 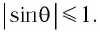 Максимальный порядок спектра
Максимальный порядок спектра 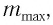 который дает дифракционная решетка при нормальном падении света на нее, определяется из условия
который дает дифракционная решетка при нормальном падении света на нее, определяется из условия 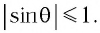

Тогда из соотношения (1) следует:
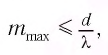
т. е. зависит от периода решетки и длины световой волны.
Таким образом, для получения спектра первого порядка 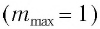 необходимо, как следует из соотношения (2), чтобы период решетки был больше длины световой волны
необходимо, как следует из соотношения (2), чтобы период решетки был больше длины световой волны 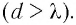
При падении на решетку белого света центральный максимум 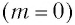 представляет собой изображение источника (рис. 67, а), так как в этом направлении собирается излучение всех длин волн. Для всех максимумов ненулевого порядка
представляет собой изображение источника (рис. 67, а), так как в этом направлении собирается излучение всех длин волн. Для всех максимумов ненулевого порядка 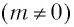 в дифракционной решетке
в дифракционной решетке 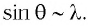 Следовательно, красные лучи, имеющие большую длину волны, чем синие, отклоняются дифракционной решеткой сильнее (рис. 67, б, в).
Следовательно, красные лучи, имеющие большую длину волны, чем синие, отклоняются дифракционной решеткой сильнее (рис. 67, б, в).
Таким образом, при освещении решетки белым светом справа и слева от центрального максимума наблюдаются максимумы первого, второго и более высоких порядков, обращенных фиолетовым краем к центру дифракционной картины, а красным от нее (см. рис. 67, а).
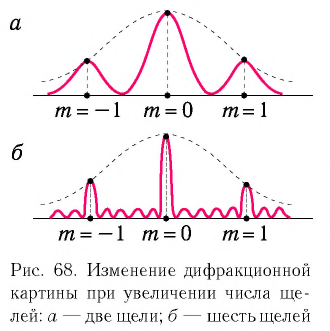
С увеличением числа щелей в дифракционной решетке возрастает количество световой энергии, пропускаемой решеткой, следовательно, интенсивность главных максимумов при этом увеличивается.
Кроме того, главные максимумы из расплывчатых превращаются в резкие и узкие, которые разделены практически темными промежутками, так как вторичные максимумы очень слабы и составляют не более 5 % от главного (рис. 68).
Отношение интенсивностей максимумов в нулевом, первом и втором порядках: 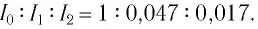 Поэтому при падении монохроматического излучения на решетки, в которых число штрихов на 1 см достигает
Поэтому при падении монохроматического излучения на решетки, в которых число штрихов на 1 см достигает 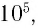 дифракционный спектр состоит из очень резких линий.
дифракционный спектр состоит из очень резких линий.
Первая дифракционная решетка, сконструированная американским ученым Риттенхаузом, состояла из параллельного ряда волосков диаметром около 0.1.мм и длиной 10 мм, натянутых на расстоянии порядка 0,2 мм один от другого. Немецкий физик Йозеф Фраунгофер вместо волосков использовал штрихи, наносимые на стекло алмазным острием. Их число на 1 мм решетки достигало у него 300.
Пример:
Дано:
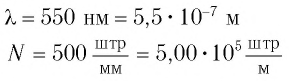
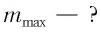
Решение:
Условие дифракционных максимумов:
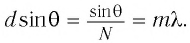
Следовательно,
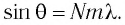
Наибольший порядок 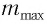 дифракционного максимума наблюдается при угле
дифракционного максимума наблюдается при угле 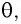 близком к углу
близком к углу 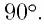 Вследствие этого будем считать, что
Вследствие этого будем считать, что
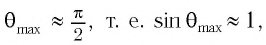
тогда наибольший порядок максимума находится по формуле:
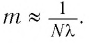
Для определения 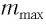 необходимо взять целую часть полученного значения:
необходимо взять целую часть полученного значения:

Ответ: 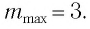
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |