
Применение матриц к расчету электрических цепей
Применение матриц к расчету электрических цепей:
Математическая символика и правила матричной алгебры позволяют упростить запись систем уравнений, получающихся при расчете сложных электрических цепей. В этом отношении матричную алгебру можно сравнить со стенографией, которая облегчает и ускоряет запись.
Напомним, что матрица представляет собой совокупность величин, называемых ее элементами и расположенных в виде прямоугольной таблицы 1. Если число строк равно числу столбцов, то матрица называется квадратной. Матрица, содержащая один столбец, называется столбцовой или матрицей-столбцом.
Приведенная система уравнений, записанных по второму закону Кирхгофа для контурных э. д. с. и контурных токов, может быть представлена в виде произведений квадратной матрицы собственных и общих сопротивлений контуров на столбцовую матрицу контурных токов.
При этом следует помнить, что произведением двух матриц называется матрица, элементы которой равны сумме произведений всех элементов соответствующей строки первой матрицы на соответствующие элементы столбца второй матрицы. Итак, уравнения (7-2) в матричной форме имеют вид: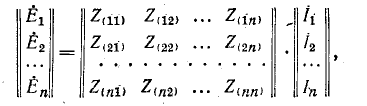
или сокращенно
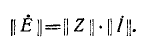
Данное матричное уравнение может быть решено относительно матрицы 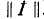 . Для этого обе стороны уравнения должны быть умножены на матрицу, обратную матрице
. Для этого обе стороны уравнения должны быть умножены на матрицу, обратную матрице 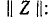
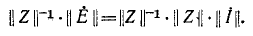 .
.
Как известно, для получения обратной матрицы необходимо заменить в исходной матрице-каждый элемент его алгебраическим дополнением, затем заменить строки соответствующими столбцами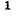 и полученную таким образом матрицу разделить на определитель исходной матрицы. Напомним, что алгебраическим дополнением элемента квадратной матрицы называется умноженный на
и полученную таким образом матрицу разделить на определитель исходной матрицы. Напомним, что алгебраическим дополнением элемента квадратной матрицы называется умноженный на 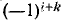 определитель, получающийся из элементов матрицы после исключения i-й строки и k-то столбца. В .свою очередь определителем матрицы называется определитель, составленный из элементов квадратной матрицы, расположенных в том же порядке, что и в матрице. Итак, обратная матрица имеет вид:
определитель, получающийся из элементов матрицы после исключения i-й строки и k-то столбца. В .свою очередь определителем матрицы называется определитель, составленный из элементов квадратной матрицы, расположенных в том же порядке, что и в матрице. Итак, обратная матрица имеет вид:
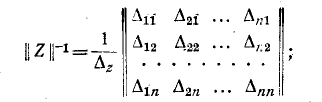
здесь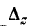 — тот же определитель системы.
— тот же определитель системы.
Произведение обратной матрицы на исходную матрицу равно единичной матрице, т. е. квадратной матрице, у которой все элементы главной диагонали (идущей от левого верхнего угла к правому нижнему) равны единице, а остальные элементы равны нулю.
Следовательно,
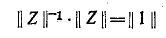
и
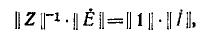
где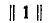 — единичная матрица.
— единичная матрица.
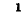 Матрица, получающаяся в результате замены строк соответствующими столбцами, называется сопряженной или транспонированной относительно исходной матрицы,
Матрица, получающаяся в результате замены строк соответствующими столбцами, называется сопряженной или транспонированной относительно исходной матрицы,
Произведение единичной матрицы на матрицу 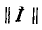 равно матрице
равно матрице 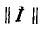 поэтому
поэтому
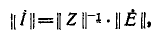
или в развернутой форме
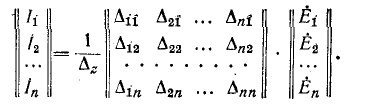
В результате умножения матриц получаются выражения для контурных токов вида (7-4).
Аналогично решается матричное уравнение для узловых напряжений
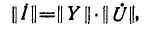
где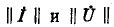 — столбцовые матрицы токов, заданных в узлах, и искомых узловых напряжений;
— столбцовые матрицы токов, заданных в узлах, и искомых узловых напряжений; 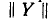 — квадратная матрица собственных и общих проводимостей узлов;
— квадратная матрица собственных и общих проводимостей узлов;
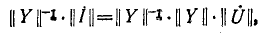
откуда
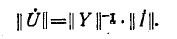
В результате умножения матрицы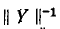 на матрицу
на матрицу 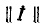 получаются выражения для узловых напряжений вида (7-6).
получаются выражения для узловых напряжений вида (7-6).
Матричная алгебра широко применяется для расчета сложных четырехполюсников.
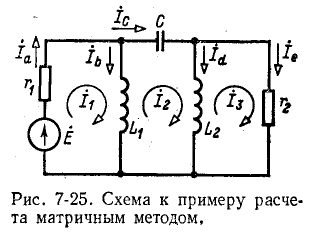
В случае относительно простой электрической схемы без взаимной индукции матрица контурных сопротивлений легко записывается непосредственно по заданной схеме. В более сложных случаях матрица контурных сопротивлений может быть получена с помощью матрицы сопротивлений ветвей. Ниже показана связь, существующая между матрицами контурных сопротивлений и сопротивлений ветвей 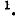 . Вывод, сделанный в общей форме, проиллюстрирован на примере простой схемы рис. 7-25, легко решаемом обычным способом.
. Вывод, сделанный в общей форме, проиллюстрирован на примере простой схемы рис. 7-25, легко решаемом обычным способом.
•Обозначим токи, напряжения, э. д. с. и сопротивления ветвей индексом «в», а соответствующие контурные величины — индексом «к». Связь между токами в ветвях и контурными токами выражается зависимостью

Здесь 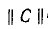 — м а т р и ц а контуров .(инциденцин). Число ее строк равно числу ветвей, а число столбцов числу контурных токов. Элементами матрицы контуров служат числа +1, — 1, и 0, +1 означает, что выбранные на схеме положительные направления тока в ветви и контурного тока совпадают; —1 берется, когда их направления различны;- наконец, 0 означает, что данная ветвь не входит в рассматриваемый контур.
— м а т р и ц а контуров .(инциденцин). Число ее строк равно числу ветвей, а число столбцов числу контурных токов. Элементами матрицы контуров служат числа +1, — 1, и 0, +1 означает, что выбранные на схеме положительные направления тока в ветви и контурного тока совпадают; —1 берется, когда их направления различны;- наконец, 0 означает, что данная ветвь не входит в рассматриваемый контур.
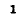 Существует также и зависимость между матрицами проводимостей
Существует также и зависимость между матрицами проводимостей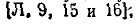
Например, для схемы рис. 7-25 имеем:
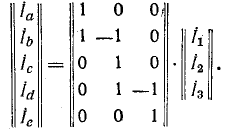
Уравнения вида (М2) по второму закону Кирхгофа в матричной форме записываются так:

где 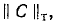 — матрица, транспонированная относительно матрицы контуров
— матрица, транспонированная относительно матрицы контуров 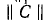 и отличающаяся от последней тем, что строки заменены столбцами.
и отличающаяся от последней тем, что строки заменены столбцами.
Строка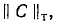 так же как и столбец || С ||, содержит кроме нулей единицы на местах, соответствующих ветвям данного контура; поэтому «произведение» ее на
так же как и столбец || С ||, содержит кроме нулей единицы на местах, соответствующих ветвям данного контура; поэтому «произведение» ее на 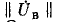 дает алгебраическую сумму напряжений ветвей этого контура. Согласно второму закону Кирхгофа алгебраическая сумма напряжений на ветвях
дает алгебраическую сумму напряжений ветвей этого контура. Согласно второму закону Кирхгофа алгебраическая сумма напряжений на ветвях
любом контуре равна нулю, т. е. «произведение» любой строки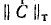 на столбец
на столбец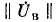 должно равняться нулю, что и выражает (7-21).
должно равняться нулю, что и выражает (7-21).
Например, для схемы рис, 7-25 имеем:
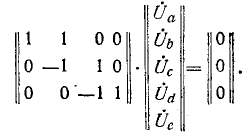
Считая, что направления э. д. с. и токов в ветвях совпадают, получаем матрицу напряжений на ветвях в виде

Подстановка (7-20) и (7-22) дает:
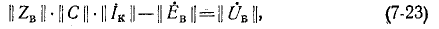
а подстановкой (7-23) в (7-21) получаем:
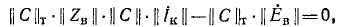
откуда
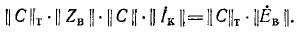
Сопоставив это уравнение с уравнением для контурных токов 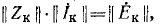
приходим к выводу, что э. д. с. в ветвях и контурные э. д. с. связаны матричным уравнением

а матрица контурных сопротивлений получается по формуле
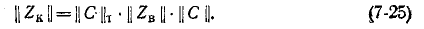
Для схемы рис. 7-25 матрица сопротивлений ветвей записывается в виде
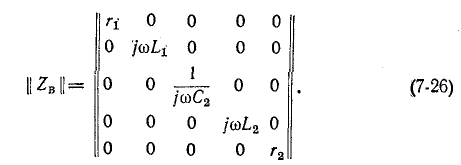
Матрица контурных сопротивлений согласно (7-25) равна:
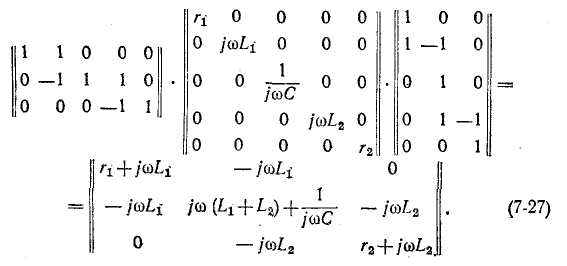
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Дуальные цепи
- Электромеханические аналогии
- Индуктивно связанные электрические цепи
- Фильтры и топологические методы анализа линейных электрических цепей
- Теорема обратимости (или взаимности)
- Теорема компенсации
- Теорема об изменении токов в электрической цепи при изменении сопротивления в одной ветви
- Теорема об эквивалентном источнике