Приложения производной функции одной переменной с примерами решения

Содержание:

Нахождение пределов функций по правилу Лопиталя:

Если при нахождении предела некоторой функции, заданной формулой, при стремлении аргумента к некоторой величине при формальной подстановке этой величины в качестве аргумента в формулу, задающую рассматриваемую функцию, получаются выражения вида

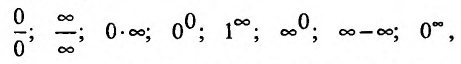
и они называются неопределенностями, т.к. в этом случае по получающимся выражениям нельзя судить о том, существует или нет указанный предел.

Способы отыскания пределов функций, называемые правилом Лопиталя

Рассмотрим некоторые способы отыскания пределов функций, называемые правилом Лопиталя.

Раскрытие неопределенностей вида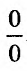

Теорема 13.1.1. Пусть функции f и g определены, дифференцируемы на полуинтервале (а, b] или на 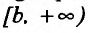и удовлетворяют следующим условиям:

• 1.
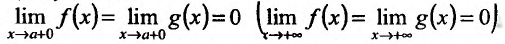
• 2. 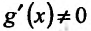для всех x принадлежащих (a, b] или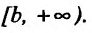

Тогда, если существует (конечный или бесконечный) предел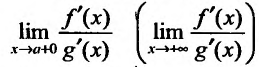то существует и предел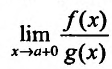

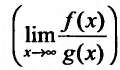причем справедливо соотношение

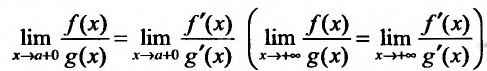
Доказательство. I. Рассмотрим случай, когда функции f и g определены на полуинтервале 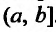. Для доказательства теоремы введем следующие вспомогательные функции

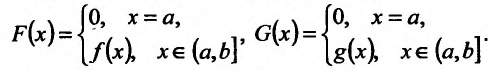
Очевидно, что для всех 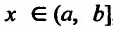выполняется равенство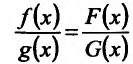

Функции F и G удовлетворяют условиям теоремы Коши: они непрерывны на отрезке [a, b] и дифференцируемы на интервале (а, b). Тогда, в силу этой теоремы, внутри интервала (а, b) существует точка 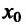такая, что

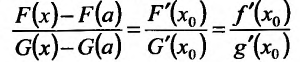
(в силу задания функхшй F и G) для любого x: из отрезка [а, b]. Ясно, что если 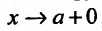, то и 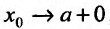, поскольку 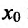находится между х и а. Поэтому, учитывая определение функций F(x) и G(x) можно записать равенство: 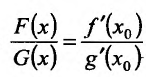: . Рассматривая предел отношения 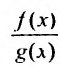, и учитывая предыдущее равенство, получим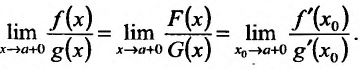

Пусть теперь функции f и g определены на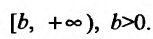

Введем новую независимую переменную по формуле 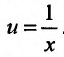. Тогда полубесконечный интервал 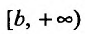преобразуется в полуинтервал 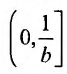, а функции f и g к виду: 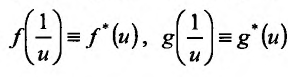, где

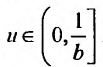
Преобразованные функции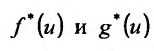 удовлетворяют теореме на полуинтервале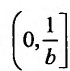, т. е. мы имеем предыдущий случай. Поэтому, в силу доказанного утверждения, справедливо равенство:

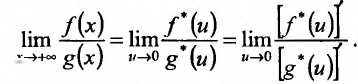
Для доказательства теоремы вычислим производные функций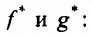

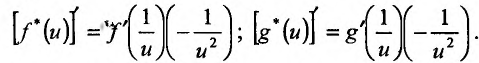
Подставляя в предыдущее равенство, получим утверждение теоремы:

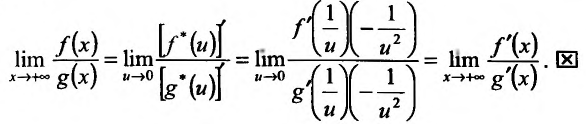
Заметим, что теорема 13.1.1. остается справедливой и для случая, когда 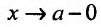с очевидными изменениями.

Пример:

Вычислить предел .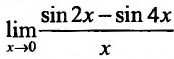

Решение:

При х=0 числитель и знаменатель дроби обращаются в нуль, поэтому имеем неопределенность вида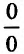. Чтобы раскрыть ее, применим правило Лопиталя, т.е. вычислим производную числителя и знаменателя и предел их отношения:

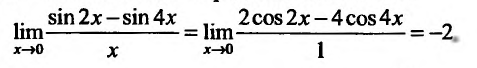
Пример:

Вычислить предел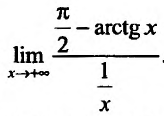

Решение:

Если 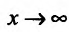, то числитель и знаменатель стремятся к нулю; имеем неопределенность вида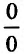. Чтобы раскрыть ее, вычислим производные числителя и знаменателя и вычислим предел их отношения:

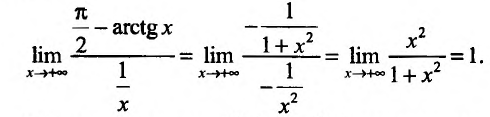
Если производные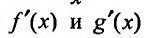 удовлетворяют тем же требованиям, что и сами функции, то правило Лопиталя можно применять повторно, т.е. предел отношения первых производных функций f(х) и g(x) можно заменить пределом отношения вторых производных этих функций:

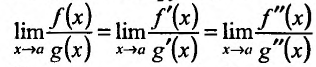
Например, следующий предел вычисляется двукратным применением правила Лопиталя: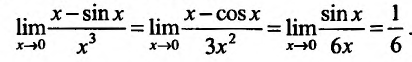

Более того, правило Лопиталя можно применять любое конечное число раз.

Трёхкратным применением правила Лопиталя вычисляется предел:

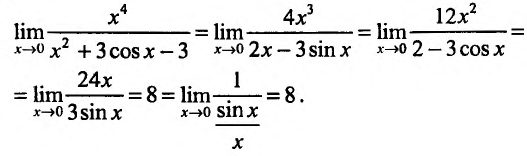
Раскрытие неопределенностей вида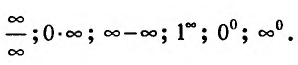

Теорема 13.1.2. Пусть функции f и g определены и дифференцируемы на полуинтервале (а, b], и удовлетворяют следующим условиям:

1.

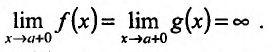
2. 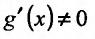для всех x, принадлежащих полуинтервалу (а, b]. Тогда, если существует (конечный или бесконечный) предел

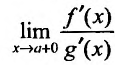, то существует и предел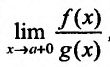, причем справедливо равенство: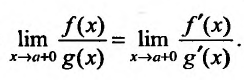

Пример:

Вычислить предел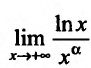, где а > 0.

Решение:

При 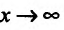числитель и знаменатель дроби неограниченно возрастают. Имеем неопределенность вида 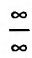. .Чтобы раскрыть ее, вычислим производную числителя знаменателя и предел их отношения: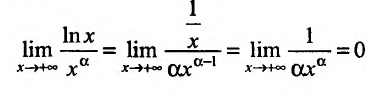

Замечание. Другие виды неопределенностей путем алгебраических преобразований сводятся к изученным выше неопределенностям 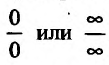. Так, например, неопределенности 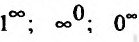раскрываются предварительным логарифмированием. Каждая из этих неопределенностей может возникнуть при вычислении предела функции:

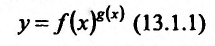где при 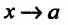функция 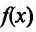стремится к 1 или к 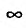, или к 0, а функция g(x) стремится соответственно к 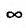или к 0. Логарифмируя выражение (13.1.1), получим (считая, что 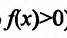)равенство: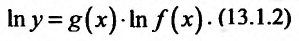

Для нахождения предела (13.1.1) достаточно найти предел выражения (13.1.2), при этом выражение (13.1.2) имеет, при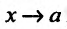, неопределенность вида 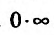. которая сводится к неопределенности

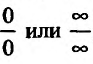, если переписать равенство (13.1.2) в виде: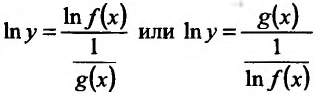

Пример:

Вычислить предел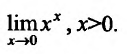

Решение:

Это неопределенность вида 0°, при 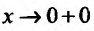. Обозначим 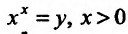, и прологарифмируем это выражение: 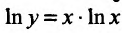Тогда искомый предел вычислим, если вычислим предел In у при:

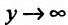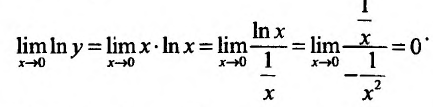
Поскольку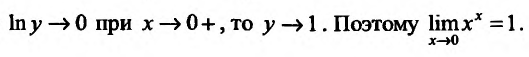

Пример:

Вычислить предел .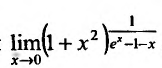

Решение:

Пусть 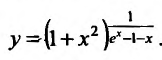Прологарифмировав это равенство, получим,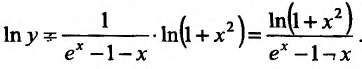

Это выражение имеет неопределенность вида 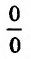при .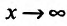

Применяя правило Лопиталя, вычислим искомый предел:

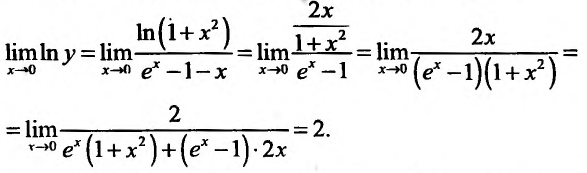
Поскольку 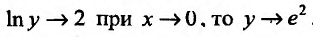, следовательно,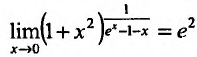

Второй замечательный предел. Докажем, применяя правило Лопиталя, что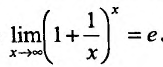

Ясно, что этот предел есть неопределенность вида 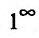. Введем обозначение 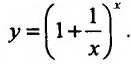. Тогда логарифмируя и проводя элементарные преобразования, получим 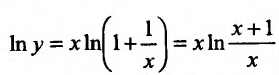• Применяя правило Лопиталя к полученному отношению, будем иметь: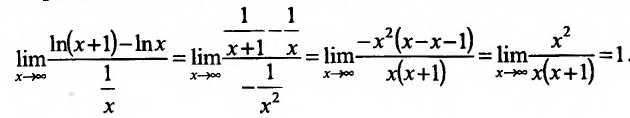

Итак,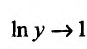. Стало быть, 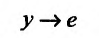и, следовательно,.

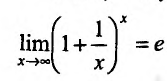Экономический смысл производной. Эластичность функции

Экономический смысл производной выясним на примерах. Известно, что издержки производства К однородной продукции есть функция количества продукции х. Поэтому можно записать К=К(х).

(Затраты труда или рабочего времени, общественно необходимого для изготовления товара и образующие его стоимость называются издержками его производства). Предположим, что количество продукции увеличилось на 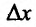, тогда продукции 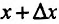соответствуют издержки производства продукции 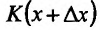. Следовательно, приращению количества продукции 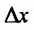соответствует приращение издержек производства продукции 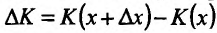Среднее приращение издержек производства равно отношению приращения издержек к приращению объёма продукции 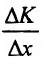(приращение издержек на единицу приращения продукции). Предел разностного отношения 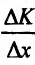при 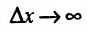одной стороны равен предельным издержкам производства, а с другой стороны производной:. Значит, предельные издержки производства определяются значением производной функции издержек.

Пример:

Пусть издержки производства К(х) от объема продукции х выражаются формулой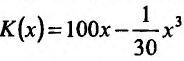

Определим предельные издержки, если объём производства составляет 10 единиц продукции.

Решение:

Поскольку предельные издержки производства определяются значением производной функции издержек, то вычисляем производную и подставляем значение х=10 в результат:

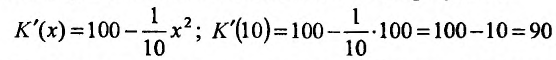
Полученное значение производной функции издержек К=К(х) при x= 10 означает, что при объеме производства в 10 единиц продукции издержки по изготовлению 11 единицы продукции составят 90.

Предположим теперь, что средние издержки производства равны предельным издержкам при увеличении производства на 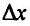. Тогда приращение издержек можно определить по формуле 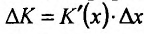. которую можно переписать в виде 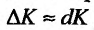. из которой следует, что если средние издержки равны предельным издержкам, то увеличение издержек производства определяется дифференциалом функции. Следовательно, мы выяснили экономический смысл дифференциала.

При помощи производной можно вычислить приращение зависимой переменной, соответствующее приращению независимой переменной. Однако во многих задачах удобнее вычислять процент прироста (относительное приращение) зависимой переменной, соответствующее проценту прироста независимой переменной. Это приводит нас к понятию эластичности функции, т.е. относительной производной.

Пусть дана функция 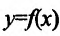. Назовем отношение 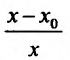относительным приращением независимой переменной, а соответствующее отношени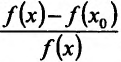е , где 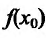- значение функции в точке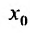, относительным приращением зависимой переменной у. Тогда отношение 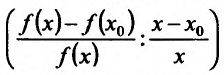относительного приращения функции к относительному приращению аргумента, показывает во сколько раз относительное приращение функции больше относительного приращения аргумента. Если существует производная функции у=f(х), то существует и предел этого отношения, т.е. 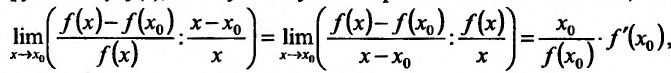который и называется эластичностью функции y=f(x) относительно переменной х, и обозначаемый 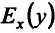. Итак,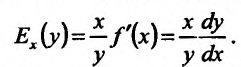

Эластичность функции относительно аргумента х есть приближенный прирост функции (повышение или понижение), соответствующий приращению независимой переменной на 1%.

Эластичность функции обладает следующими свойствами:

Теорема 13.2.1. Эластичность произведения двух функций u и v равняется сумме показателей эластичности сомножителей.

Доказательство. Пусть заданы две функции и и v, характеризующие некоторые экономические зависимости. Рассмотрим функцию f= uv. Тогда по определению эластичности имеем:

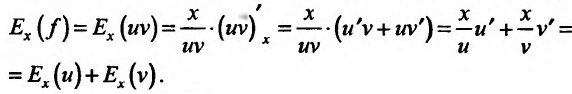
Теорема доказана.

Теорема 13.2.2. Эластичность частного двух функциц u и v равняется разности показателей эластичности делимого и делителя.

Доказательство. Пусть заданы две функции u и v, характеризующие некоторые экономические зависимости. Рассмотрим функцию 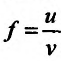. Воспользовавшись определением эластичности, получим: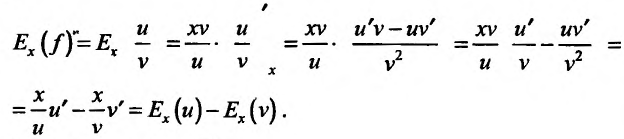

Теорема доказана

Эластичность спроса относительно цены

Предположим, что цена товаров (кроме одного), доходы потребителей и структура потребностей - постоянные величины. Тогда между спросом на данный товар (цена которого изменяется) и его иеной можно установить функциональную зависимость: q=f(p) , где q - спрос, р - цена. Однако, во многих экономических исследованиях необходимо определить не величину спроса, а изменение спроса, вызываемое изменением цены, т.е. определить эластичность функции спроса относительно цены.

Ясно, что если произойдет изменение цены на 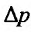, то и спрос изменится на . Составим частное, которое выражает относительное изменение спроса, если цена товара изменится на 1%, 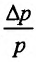- относительное изменение цены; 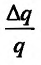- относительное изменение спроса). По определению эластичности, получим:

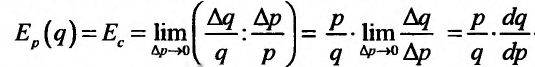
Итак, эластичность спроса относительно йены приблизительно определяет, как изменится спрос на данный товар, если его цена возрастет на 1% и вычисляется по формуле:

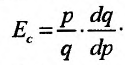
В большинстве случаев функция спроса - убывающая функция, т.к. с повышением цены спрос понижается, поэтому

Следует отметить, что если:

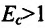1. , т.е. если повышению цены на 1% соответствует снижение спроса более чем на 1%, то говорят, что спрос эластичен;
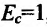2. , т.е. если повышению цены на 1% соответствует снижение спроса на 1%, то спрос нейтрален;
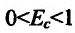3. , т.е. если повышению цены на 1% соответствует понижение спроса менее чем на 1%, то говоря!, что спрос неэластичен.

Кроме того, так как эластичность спроса - функция, то разным ценам соответствуют разные показатели эластичности спроса.

• Заказать решение задач по высшей математике

Пример:

Пусть функция спроса q= 7 -р. Определим, как изменится спрос на товар при цене 2 ден.ед.

Решение:

Воспользуемся формулой (13.3.1) и вычислим значсние эластичности: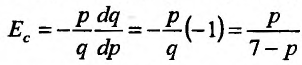

Подставив значение цены 2 ден. ед. в эластичность, получим: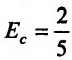. Это означает, что при цене 2 ден. ед. повышение цены на 1% вызовет снижение спроса на .

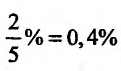Эластичность спроса относительно дохода

Предположим, что доход потребителей изменяется, а структура потребностей и цена товаров не меняется. Тогда спрос q есть функция дохода 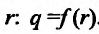. Ясно, что если доходы возрастут на 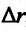, то спрос увеличится на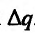. Поэтому частное 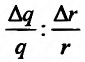означает относительный прирост спроса. А эластичностью спроса относительно дохода, согласно определению эластичности, называется выражение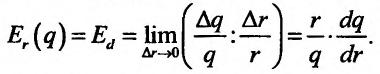

Итак, эластичность спроса относительно дохода есть мера реакции спроса на изменение доходов потребителей

Важной проблемой при этом будет изменение спроса на тот или другой товар с ростом заработной платы. В этом случае необходимо знать эластичность спроса этого товара относительно дохода, т.к. с ростом заработной платы начинает возрастать спрос на более качественные товары.

Например, предположим, что государство предполагает повысить цену какого-либо товара на 10%. Если известно, что эластичность спроса составляет 0,2 (относительно дохода), то следует ожидать, что это вызовет снижение спроса на данный товар на 2%. В результате доход государства повысился бы на 8%.

Пример:

Пусть известны функции спроса d=7-p и функция предложения s=p+l, где р - цена. Нужно найти равновесную цену и эластичности спроса и предложения.

Решение:

Равновесная цена определяется из условия d=s, т.е. когда спрос равен предложению, поэтому 7-р=р+1, откуда р=3. Найдем эластичность спроса и предложения:

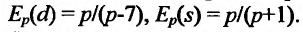
Для равновесной цены р=3 получим 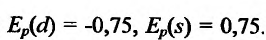. Для значения р =3 спрос является неэластичным, также как и функция предложения.

Упражнение 13.4.1. Пусть функции спроса 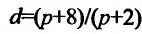, и предложения 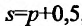, где р -цена товара. Найти равновесную цену и эластичность спроса и предложения для этой цены.

Предложение и эластичность предложения

Определение 13.5.1. Предложением называется количество данного товара, предлагаемого на продажу в единицу времени.

Эластичность предложения можно определить аналогично эластичности спроса. Действительно, если s=s(p) - функция предложения, то при изменении цены на 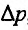, изменяется и предложение на 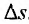. Рассматривая предел отношения относительного прироста предложения 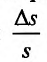и относительно приращения цены 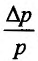, если 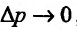, получим эластичность предложения: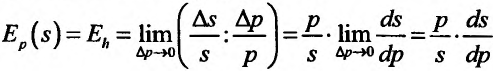

Итак, эластичность предложения относительно цены приблизительно определяет процент прироста предложения на 1% прироста цены.

Формулы Тейлора и Маклорена

Рассмотрим одну из важнейших формул математического анализа, имеющую многочисленные применения, как в математике, так и в смежных дисциплинах.

При изучении вопроса о дифференцировании функций в точке установлено, что если функция f имеет в точке 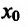производную, то ее приращение можно представить в виде:

,

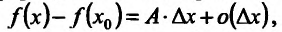где .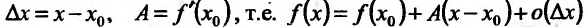

Иначе говоря, существует линейная функция 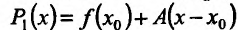, такая, что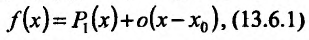

причем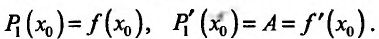

Предположим теперь, что функция f имеет в точке 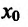n производных. Естественно, по аналогии с предыдущим, предположить, что существует многочлен 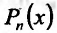степени n такой, что

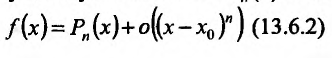
и

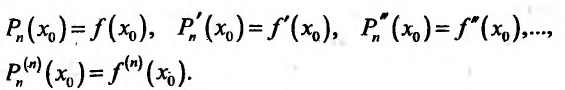(13.6.3)

Будем искать этот многочлен в виде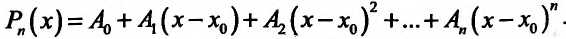

Полагая 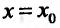, получим 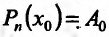, откуда в силу (13.6.3) найдем значение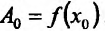. Далее, вычислим производную 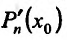и положим 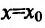в значении производной: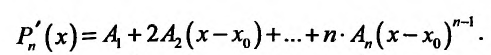

Получим 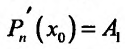, и так как 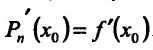, то .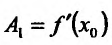

Затем находим вторую производную многочлена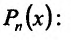

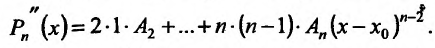
При 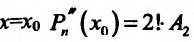и из условия 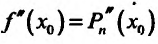находим

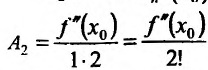Продолжая вычислять производные и ис-

пользуя условие (13.6.3) найдем значения коэффициентов многочлена 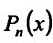. В общем случае: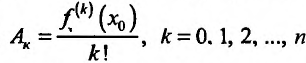

Таким образом, мы нашли значения коэффициентов, т.е. построили многочлен

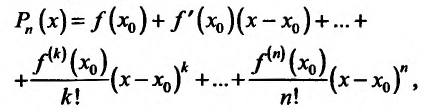
который удовлетворяет условию (13.6.3). Теперь проверим, удовлетворяет ли он условию (13.6.2). Обозначим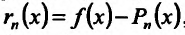, и выясним порядок малости 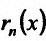относительно .

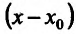Для этого рассмотрим предел 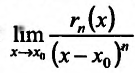, который вычислим, применяя правило Лопиталя и используя условие:

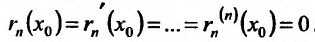
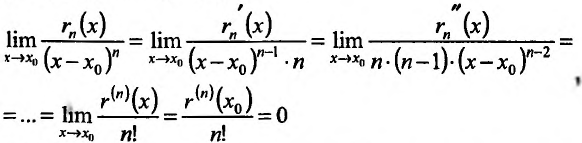
т.е. 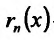- бесконечно малая величина при 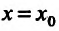порядка малости выше, чем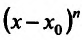

Итак, доказана

Теорема 13.6.1. Если функция f определенная на интервале (а, b) имеет в точке 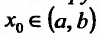производные до порядка n включительно, то

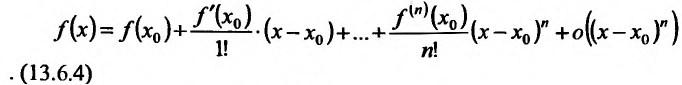
Многочлен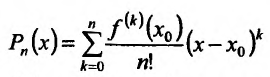 называется многочеленом Тейлора, а 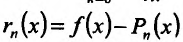остаточным членом n- ого порядка формулы Тейлора. Существует несколько видов остаточного члена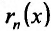. Мы рассмотрим формулу Тейлора с остаточным членом в форме Лагранжа:

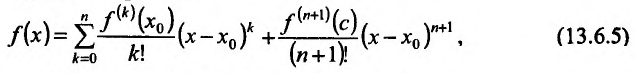где точка с расположена между точками х и .

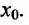Если 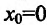, то получается частный вид формулы Тейлора, называемый формулой Маклорена:

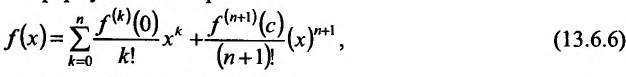где точка с расположена между 0 и х