
Приложения производной с примерами решения
Содержание:
Прежде чем перейти к наиболее важным приложениям производной при исследовании функций и построении их графиков, рассмотрим несколько основных теорем.
Основные теоремы дифференциального исчисления
Теорема Ферма
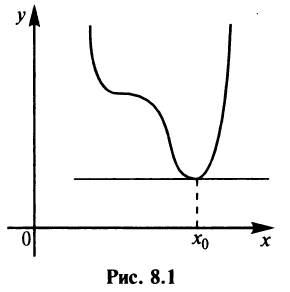
Теорема Ферма. Если дифференцируемая на промежутке 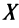
 Пусть функция
Пусть функция 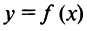 дифференцируема на промежутке
дифференцируема на промежутке 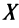 в точке
в точке 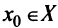 принимает наименьшее значение (рис. 8.1).
принимает наименьшее значение (рис. 8.1).
Тогда 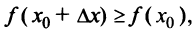 если
если 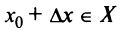 и, следовательно, величина
и, следовательно, величина 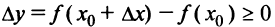 при достаточно малых
при достаточно малых 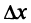 независимо от знака
независимо от знака 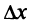 . Отсюда
. Отсюда 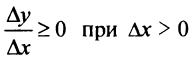 и
и 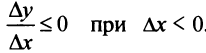 Переходя к пределу при
Переходя к пределу при  (справа) и при
(справа) и при 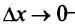 (слева), получим
(слева), получим 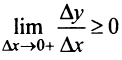 и
и 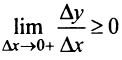 .
.
По условию функция 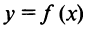 дифференцируема в точке
дифференцируема в точке 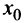 , следовательно, ее предел при
, следовательно, ее предел при 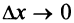 не должен зависеть от способа стремления
не должен зависеть от способа стремления 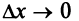 (справа или слева), т.е.
(справа или слева), т.е.

Аналогично рассматривается случай, когда функция 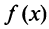 принимает в точке x
принимает в точке x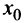 наибольшее значение. ■
наибольшее значение. ■
Геометрический смысл теоремы Ферма очевиден: в точке наибольшего или наименьшего значения, достигаемого внутри промежутка 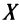 , касательная к графику функции параллельна оси абсцисс.
, касательная к графику функции параллельна оси абсцисс.
Теорема Ферма может быть использована для доказательства так называемых теорем о среднем, к рассмотрению которых мы переходим.
Теорема Ферма дополнительное подробное объяснение:
Пусть функция у=f(х), непрерывная в некотором интервале 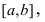 принимает свое наибольшее (или наименьшее) значение во внутренней точке с данного интервала:
принимает свое наибольшее (или наименьшее) значение во внутренней точке с данного интервала: 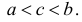 Если в точке с производная функции f(х) существует, то она равна нулю
Если в точке с производная функции f(х) существует, то она равна нулю 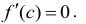
Доказательство. Если функция f(х) принимает свое наибольшее значение в точке с, то это значит, что касательная к графику функции в точке с параллельна оси абсцисс, т.е. угол между касательной и осью абсцисс равен нулю. Из геометрического смысла производной непосредственно следует, что 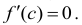
Теорема Ролля
Теорема Ролля. Пусть функция 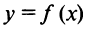 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
- 1) непрерывна на отрезке
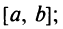
- 2) дифференцируема на интервале
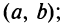
- 3) на концах отрезка принимает равные значения, т.е.
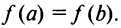
Тогда внутри отрезка существует по крайней мере одна такая точка 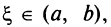 в которой производная функции равна нулю:
в которой производная функции равна нулю: 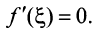
На основании теоремы Вейерштрасса (см. § 6.7) функция, непрерывная на отрезке, достигает на нем своего наибольшего 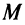 и наименьшего
и наименьшего 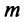 значений. Если оба эти значения достигаются на концах отрезка, то по условию они равны (т.е.
значений. Если оба эти значения достигаются на концах отрезка, то по условию они равны (т.е. 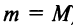 ), а это значит, что функция тождественно постоянна на отрезке
), а это значит, что функция тождественно постоянна на отрезке 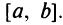 Тогда производная равна нулю во всех точках этого отрезка. Если же хотя бы одно из этих значений — максимальное или минимальное — достигается внутри отрезка (т.е.
Тогда производная равна нулю во всех точках этого отрезка. Если же хотя бы одно из этих значений — максимальное или минимальное — достигается внутри отрезка (т.е. 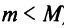 ), то производная в соответствующей точке равна нулю в силу теоремы Ферма. ■
), то производная в соответствующей точке равна нулю в силу теоремы Ферма. ■
Отметим геометрический смысл теоремы Ролля (см. рис. 8.2): найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс, в этой точке производная и будет равна нулю (заметим, что на рис. 8.2 таких точек две: 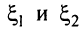 )•
)•
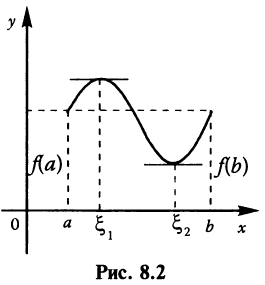
Если 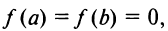 то теорему Ролля можно сформулировать так: между двумя последовательными нулями дифференцируемой функции имеется хотя бы один нуль производной.
то теорему Ролля можно сформулировать так: между двумя последовательными нулями дифференцируемой функции имеется хотя бы один нуль производной.
Следует отметить, что все условия теоремы Ролля существенны и при невыполнении хотя бы одного из них заключение теоремы может оказаться неверным. Так, для функций, приведенных на рис. 8.3, нарушено только одно условие: на рис. 8.3а — непрерывность на отрезке 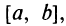 на рис. 8.36 — дифференцируемость на интервале
на рис. 8.36 — дифференцируемость на интервале 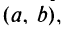 на рис. 8.3в — равенство значений
на рис. 8.3в — равенство значений 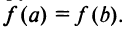
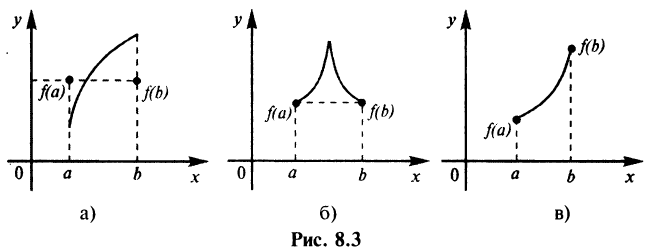
В результате не существует такой точки 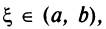 в которой
в которой 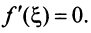
Теорема Ролля является частным случаем теоремы Лагранжа.
Теорема Ролля дополнительное подробное объяснение:
Если функция f(x) непрерывна в замкнутом интервале 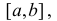 , дифференцируема во всех его внутренних точках и имеет на концах интервала х = а и х = b равные значения, то существует внутри указанного интервала, по крайней мере, одна точка
, дифференцируема во всех его внутренних точках и имеет на концах интервала х = а и х = b равные значения, то существует внутри указанного интервала, по крайней мере, одна точка 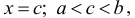 в которой производная f'(x) обращается в нуль, т.е. f'(с) = 0.
в которой производная f'(x) обращается в нуль, т.е. f'(с) = 0.
Замечание. Данная теорема справедлива и для такой дифференцируемой функции, у которой значения на концах отрезка равны и не обязательно равны 0.
Теорема Лагранжа
Теорема Лагранжа. Пусть функция 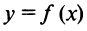 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
- 1) непрерывна на отрезке
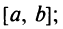
- 2) дифференцируема на интервале
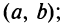
Тогда внутри отрезка существует по крайней мере одна такая точка 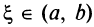 , в которой производная равна частному от деления приращения функции на приращение аргумента на этом отрезке, т.е.
, в которой производная равна частному от деления приращения функции на приращение аргумента на этом отрезке, т.е.
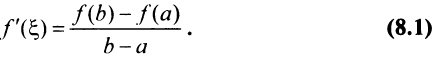
Введем новую функцию 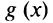 следующим образом:
следующим образом:
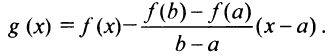
Функция 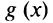 удовлетворяет условиям теоремы Ролля: она непрерывна на отрезке
удовлетворяет условиям теоремы Ролля: она непрерывна на отрезке 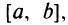 дифференцируема на интервале
дифференцируема на интервале 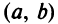 и принимает на его концах равные значения:
и принимает на его концах равные значения:
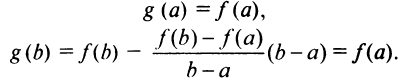
Следовательно, существует точка 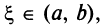 такая, что
такая, что 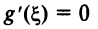
или 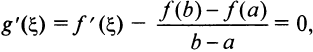 откуда
откуда 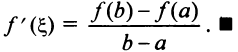
Заключение (8.1) теоремы Лагранжа может быть записано и в виде:
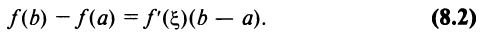
Выясним механический и геометрический смысл теоремы Лагранжа.
Приращение 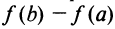 — это изменение функции на отрезке
— это изменение функции на отрезке
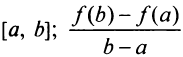 —средняя скорость изменения функции на этом отрезке; значения же производной в точке — это «мгновенная» скорость изменения функции. Таким образом, теорема утверждает: существует хотя бы одна точка внутри отрезка, такая, что скорость изменения функции в ней равна средней скорости изменения функции на этом отрезке.
—средняя скорость изменения функции на этом отрезке; значения же производной в точке — это «мгновенная» скорость изменения функции. Таким образом, теорема утверждает: существует хотя бы одна точка внутри отрезка, такая, что скорость изменения функции в ней равна средней скорости изменения функции на этом отрезке.
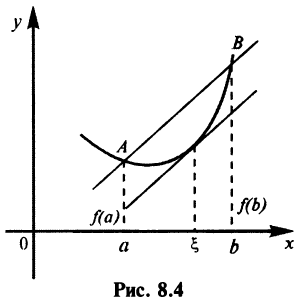
Геометрическая интерпретация теоремы Лагранжа приведена на рис. 8.4.
Если перемещать прямую  параллельно начальному положению, найдется хотя бы одна точка
параллельно начальному положению, найдется хотя бы одна точка 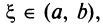 в которой касательная к графику
в которой касательная к графику 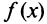 и хорда
и хорда 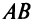 , проведенная через концы дуги
, проведенная через концы дуги 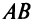 , параллельны (ибо в соответствии с (4.5) угловой коэффициент секущей
, параллельны (ибо в соответствии с (4.5) угловой коэффициент секущей 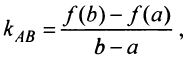 а касательной —
а касательной — 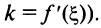
Следствие. Если производная функции 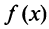 равна нулю на некотором промежутке X, то функция тождественно постоянна на этом промежутке.
равна нулю на некотором промежутке X, то функция тождественно постоянна на этом промежутке.
 Возьмем на рассматриваемом промежутке X отрезок
Возьмем на рассматриваемом промежутке X отрезок 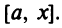 Согласно теореме Лагранжа
Согласно теореме Лагранжа 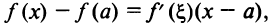 где
где 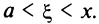 По условию
По условию 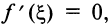 следовательно,
следовательно, 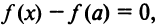 т.е.
т.е. 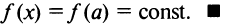
Теорема Лагранжа дополнительное подробное объяснение:
Если функция f(x) непрерывна в замкнутом интервале 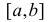 и дифференцируема во его всех внутренних точках, то внутри указанного интервала найдется, по крайней мере, одна точка
и дифференцируема во его всех внутренних точках, то внутри указанного интервала найдется, по крайней мере, одна точка 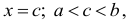 что
что
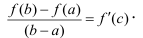
Геометрический смысл равенства из теоремы состоит в следующем: отношение 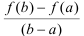 есть угловой коэффициент хорды АВ или тангенс угла наклона хорды АВ, a f'(c) - есть угловой коэффициент касательной или тангенс угла наклона касательной, проведенной к графику в точке с абсциссой с.
есть угловой коэффициент хорды АВ или тангенс угла наклона хорды АВ, a f'(c) - есть угловой коэффициент касательной или тангенс угла наклона касательной, проведенной к графику в точке с абсциссой с.
Теорема Лагранжа утверждает, что если во всех точках дуги АВ существуют касательные, то на этой дуге найдется точка С между А и В, в которой касательная параллельна хорде, соединяющей точки А и В.
Данное утверждение согласуется с приведенным рисунком 4.1.
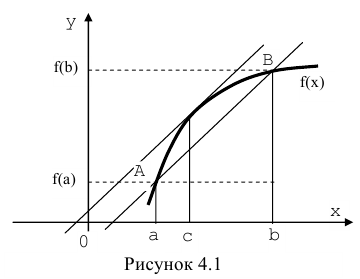
Правило Лопиталя
Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.
Итак, если имеется неопределенность вида 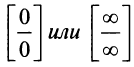 то
то
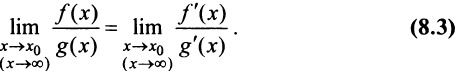
 Рассмотрим доказательство теоремы для неопределенности
Рассмотрим доказательство теоремы для неопределенности
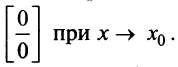
Для простоты будем предполагать, что функции 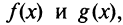 а также их производные непрерывны в точке
а также их производные непрерывны в точке 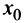 , причем
, причем 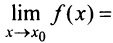
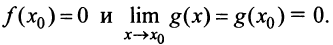
В этом случае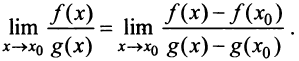
Применяя теорему Лагранжа для функций 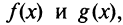 на отрезке
на отрезке 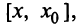 получим
получим
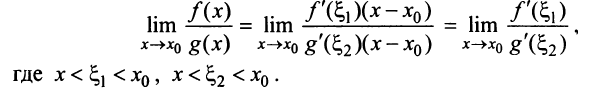
При 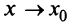 в силу непрерывности производных
в силу непрерывности производных 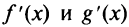 имеем
имеем 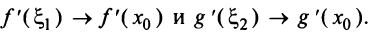 Используя теорему о пределе частного двух функций, получаем равенство (8.3). ■
Используя теорему о пределе частного двух функций, получаем равенство (8.3). ■
Замечание. Обращаем внимание, что в правой части формулы (8.3) берется отношение производных, а не производная отношения.
Пример №1
Найти:
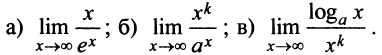
Решение:
а) Имеем неопределенность вида 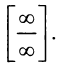 правило Лопиталя, получим:
правило Лопиталя, получим:
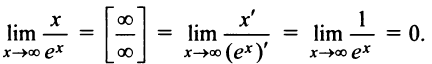
б) Имеем также неопределенность вида 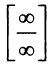 .Применим правило Лопиталя
.Применим правило Лопиталя 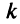 раз, если
раз, если 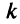 — целое, и
— целое, и 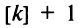 раз, если
раз, если 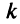 — нецелое (где [
— нецелое (где [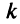 ] — целая часть числа
] — целая часть числа 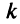 ):
):
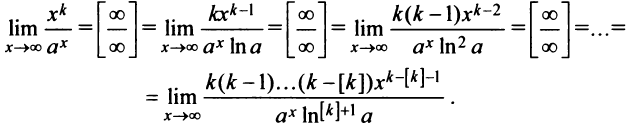
При каждом применении правила Лопиталя степень числителя будет уменьшаться на единицу и через 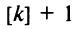 раз станет отрицательной, т.е. числитель обратится в бесконечно малую величину (если
раз станет отрицательной, т.е. числитель обратится в бесконечно малую величину (если 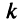 — не целое число; если
— не целое число; если 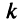 — целое, то в постоянную величину). Знаменатель же будет оставаться бесконечно большой величиной. Таким образом,
— целое, то в постоянную величину). Знаменатель же будет оставаться бесконечно большой величиной. Таким образом, 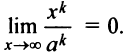
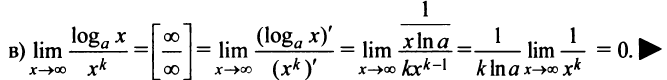
Правило Лопиталя дает возможность сравнения бесконечно больших величин: степенная функция 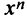 — бесконечно большая более высокого порядка, чем логарифмическая
— бесконечно большая более высокого порядка, чем логарифмическая 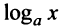 , а показательная
, а показательная 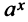 — бесконечно большая более высокого порядка, чем степенная
— бесконечно большая более высокого порядка, чем степенная 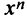 ; это означает,что
; это означает,что
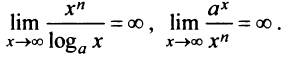
Пример №2
Найти:
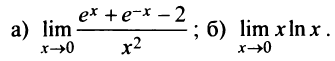
Решение:
а)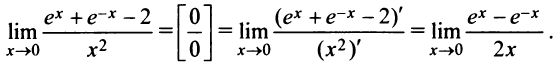
Неопределенность вида 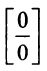 по-прежнему сохраняется. Применим правило Лопиталя еще раз:
по-прежнему сохраняется. Применим правило Лопиталя еще раз:
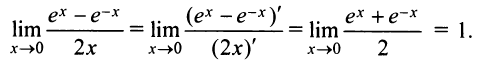
б) Имеем неопределенность вида 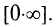 Переписывая данное выражение в виде
Переписывая данное выражение в виде
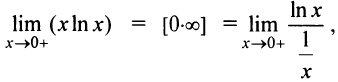 получим неопределенность вида
получим неопределенность вида 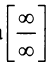 .
.
Применяя правило Лопиталя, получим 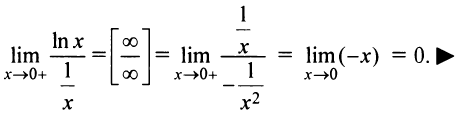
Правило Лопиталя является эффективным методом раскрытия неопределенностей. Однако применение его не всегда приводит к цели.
Пример №3
Найти:
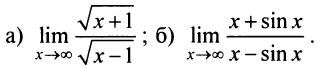
Решение:
а) Если применить правило Лопиталя, то получим
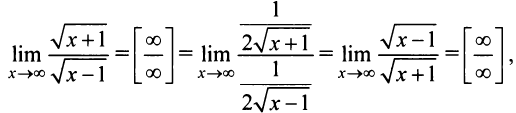
т.е. числитель и знаменатель просто меняются местами; неопределенность же сохраняется. Если применить правило Лопиталя вторично, то функция под знаком предела примет первоначальный вид. Таким образом, применение этого правила в данном случае не позволяет раскрыть неопределенность. В то же время легко установить, что 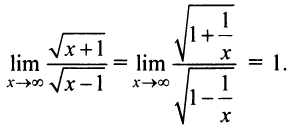 б) Если применить правило Лопиталя, т.е.
б) Если применить правило Лопиталя, т.е.
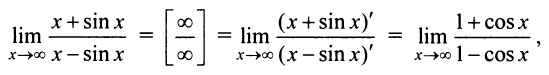 то можно сделать ошибочный вывод о том, что предел данной функции не существует, так как не существует
то можно сделать ошибочный вывод о том, что предел данной функции не существует, так как не существует 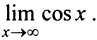
На самом деле 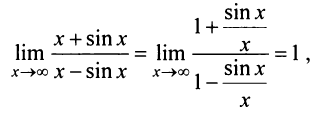
так как 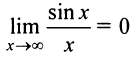 (см. пример 6.8в). ►
(см. пример 6.8в). ►
Теорема Коши
Если функции f(х) и 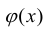 непрерывны в замкнутом интервале
непрерывны в замкнутом интервале 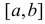 и дифференцируемы во всех его внутренних точках
и дифференцируемы во всех его внутренних точках 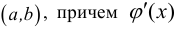 нигде
нигде
внутри интервала не обращается в нуль, то в этом интервале найдется хотя бы одна точка 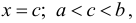 что
что
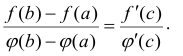
Заметим, что 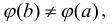 т.к. в противном случае по теореме Ролля существовала бы внутри этого интервала точка, в которой производная
т.к. в противном случае по теореме Ролля существовала бы внутри этого интервала точка, в которой производная 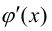 обращалась бы в нуль, а это противоречит условиям теоремы.
обращалась бы в нуль, а это противоречит условиям теоремы.
Возрастание и убывание функций
Напомним (см. § 5.3), что функция 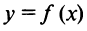 называется возрастающей (убывающей) на промежутке
называется возрастающей (убывающей) на промежутке 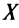 , если для любых
, если для любых 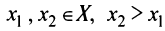 верно неравенство
верно неравенство 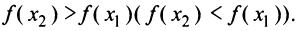
Теорема (достаточное условие возрастания функции)
Теорема (достаточное условие возрастания функции). Если производная дифференцируемой функции положительна внутри некоторого промежутка 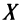 , то она возрастает на этом промежутке.
, то она возрастает на этом промежутке.
 Рассмотрим два значения
Рассмотрим два значения 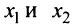 на данном промежутке
на данном промежутке 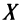 . Пусть
. Пусть 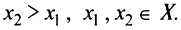 Докажем, что
Докажем, что 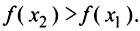
Для функции 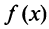 на отрезке
на отрезке 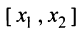 выполняются условия теоремы Лагранжа, поэтому
выполняются условия теоремы Лагранжа, поэтому
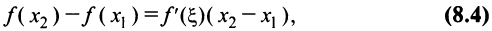
где 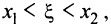 т.е.
т.е. 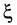 принадлежит промежутку, на котором производная положительна, откуда следует, что
принадлежит промежутку, на котором производная положительна, откуда следует, что 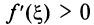 и правая часть равенства (8.3) положительна. Отсюда
и правая часть равенства (8.3) положительна. Отсюда 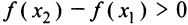 и
и 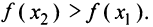 ■
■
Аналогично доказывается другая теорема.
Теорема (достаточное условие убывания функции)
Теорема (достаточное условие убывания функции): Если производная дифференцируемой функции отрицательна внутри некоторого промежутка  , то она убывает на этом промежутке.
, то она убывает на этом промежутке.
Геометрическая интерпретация условия монотонности функции приведена на рис. 8.5.
Если касательные к кривой в некотором промежутке направлены под острыми углами к оси абсцисс (рис. 8.5а), то функция возрастает, если под тупыми (рис. 8.56), то убывает. 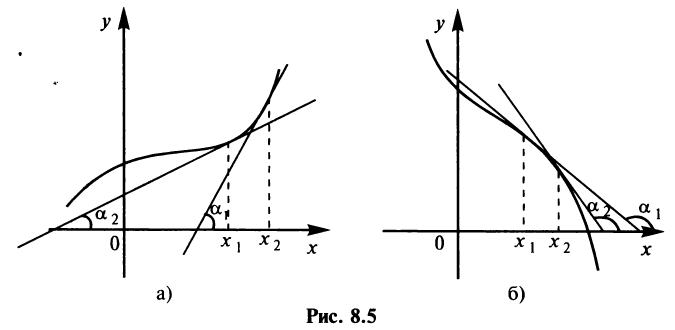
Пример №4
Найти интервалы монотонности функции 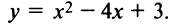
Решение:
Имеем 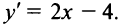 Очевидно
Очевидно 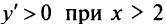 и
и 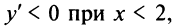 т.е. функция убывает на интервале
т.е. функция убывает на интервале 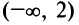 и возрастает на интервале
и возрастает на интервале 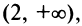 где
где 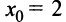 — абсцисса вершины параболы. ►
— абсцисса вершины параболы. ►
Заметим, что необходимое условие монотонности более слабое. Если функция возрастает (убывает) на некотором промежутке 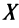 , то можно лишь утверждать, что производная неотрицательна (неположительна) на этом промежутке:
, то можно лишь утверждать, что производная неотрицательна (неположительна) на этом промежутке: 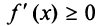
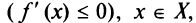 т.е. в отдельных точках производная монотонной функции может равняться нулю.
т.е. в отдельных точках производная монотонной функции может равняться нулю.
Пример №5
Найти интервалы монотонности функции 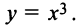
Решение:
Найдем производную 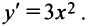 Очевидно, что
Очевидно, что 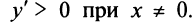 При
При 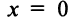 производная обращается в нуль. Функция же монотонно возрастает на всей числовой оси (см. рис. 5.5). ►
производная обращается в нуль. Функция же монотонно возрастает на всей числовой оси (см. рис. 5.5). ►
Экстремум функции
В определенном смысле материал этого параграфа наиболее важен для решения задачи исследования функций и построения их графиков. Мы выделим наиболее важные, «узловые», точки функции, нахождение которых во многом определяет структуру графика. Это точки экстремума — максимума и минимума функции.
Определение 1. Точка 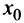 называется точкой максимума функции
называется точкой максимума функции 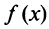 , если в некоторой окрестности точки
, если в некоторой окрестности точки 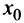 выполняется неравенство
выполняется неравенство 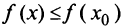 (см. рис. 8.6).
(см. рис. 8.6).
Определение 2. Точка 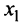 называется точкой минимума функции
называется точкой минимума функции 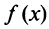 , если в некоторой окрестности точки
, если в некоторой окрестности точки 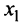 выполняется неравенство
выполняется неравенство 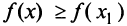 (см. рис. 8.6).
(см. рис. 8.6).
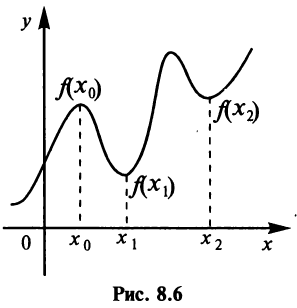
Значения функции в точках 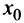 и
и 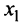 называются соответственно максимумом и минимумом функции. Максимум и минимум функции объединяются общим названием экстремума функции.
называются соответственно максимумом и минимумом функции. Максимум и минимум функции объединяются общим названием экстремума функции.
Экстремум функции часто называют локальным экстремумом, подчеркивая тот факт, что понятие экстремума связано лишь с достаточно малой окрестностью точки 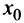 . Так что на одном промежутке функция может иметь несколько экстремумов, причем может случиться, что минимум в одной точке больше максимума в другой, например на рис.8.6
. Так что на одном промежутке функция может иметь несколько экстремумов, причем может случиться, что минимум в одной точке больше максимума в другой, например на рис.8.6 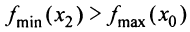 . Наличие максимума (или минимума) в отдельной точке промежутка
. Наличие максимума (или минимума) в отдельной точке промежутка 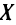 вовсе не означает, что в этой точке функция
вовсе не означает, что в этой точке функция 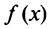 принимает наибольшее (наименьшее) значение на этом промежутке (или, как говорят, имеет глобальный максимум (минимум)).
принимает наибольшее (наименьшее) значение на этом промежутке (или, как говорят, имеет глобальный максимум (минимум)).
Важность точек экстремума иллюстрируется следующим примером (см. рис. 8.7).
Предположим, график функции 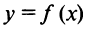 имеет вид, изображенный на рисунке сплошной линией. Допустим, мы строим его по точкам, и на рисунок нанесены точки 1, 3, 5, 7, 9. Тогда скорее всею мы получим кривую, изображенную пунктиром, которая совершенно не похожа на истинный график функции
имеет вид, изображенный на рисунке сплошной линией. Допустим, мы строим его по точкам, и на рисунок нанесены точки 1, 3, 5, 7, 9. Тогда скорее всею мы получим кривую, изображенную пунктиром, которая совершенно не похожа на истинный график функции 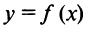 .
.
Если же на рисунок нанесены точки 2, 4, 6, 8, то качественная картина графика определена практически однозначно (по крайней мере на промежутке, содержащем эти точки).
Необходимое условие экстремума
Если в точке 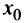 дифференцируемая функция
дифференцируемая функция 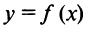 имеет экстремум, то в некоторой окрестности этой точки выполнены условия теоремы Ферма (см. § 8.1), и, следовательно, производная функции в этой точке равна нулю, т.е.
имеет экстремум, то в некоторой окрестности этой точки выполнены условия теоремы Ферма (см. § 8.1), и, следовательно, производная функции в этой точке равна нулю, т.е. 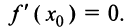 Но функция может иметь экстремум и в точках, в которых она не дифференцируема. Так, например, функция
Но функция может иметь экстремум и в точках, в которых она не дифференцируема. Так, например, функция 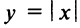 имеет экстремум (минимум) в точке
имеет экстремум (минимум) в точке 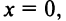 но не дифференцируема в ней (см. пример 7.2 и рис. 7.5). А функция
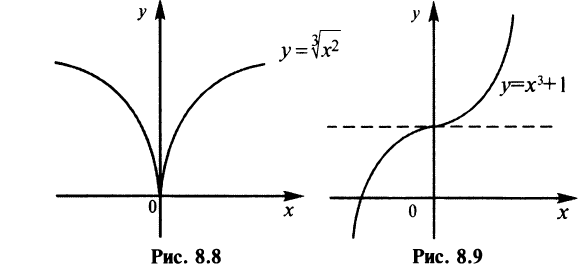
но не дифференцируема в ней (см. пример 7.2 и рис. 7.5). А функция 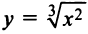 также имеет в точке
также имеет в точке 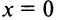 минимум (рис. 8.8), а производная ее
минимум (рис. 8.8), а производная ее 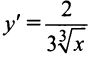 в этой точке бесконечна:
в этой точке бесконечна: 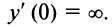 .
.
Поэтому необходимое условие экстремума может быть сформулировано следующим образом.
Для того чтобы функция  имела экстремум в точке
имела экстремум в точке 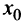 , необходимо, чтобы ее производная в этой точке равнялась нулю
, необходимо, чтобы ее производная в этой точке равнялась нулю 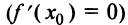 или не существовала.
или не существовала.
Точки, в которых выполнено необходимое условие экстремума, т.е. производная равна нулю или не существует, называются критическими (или стационарными'). Обращаем внимание на то, что эти точки должны входить в область определения функции.
Таким образом, если в какой-либо точке имеется экстремум, то эта точка критическая. Очень важно, однако, заметить, что обратное утверждение неверно. Критическая точка вовсе не обязательно является точкой экстремума.
Пример №6
Найти критические точки функции и убедиться в наличии или отсутствии экстремума в этих точках:
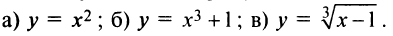
Решение:
а) Производная 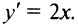 В точке
В точке 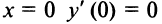 и действительно в точке
и действительно в точке 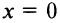 функция
функция 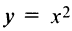 имеет экстремум (см. рис. 5.6).
имеет экстремум (см. рис. 5.6).
б) Функция 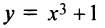 возрастает на всей числовой оси по свойству степенной функции. Производная
возрастает на всей числовой оси по свойству степенной функции. Производная 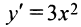 в точке
в точке 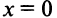 равна нулю, т.е.
равна нулю, т.е. 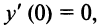 но экстремума в точке
но экстремума в точке 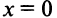 нет (см. рис. 8.9).
нет (см. рис. 8.9).
в) Функция 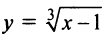 также возрастает на всей числовой оси; производная
также возрастает на всей числовой оси; производная 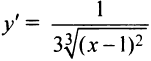 при
при 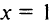 не существует, т.е.
не существует, т.е. 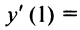
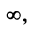 но экстремума в этой точке нет (см. рис. 8.10). ►
но экстремума в этой точке нет (см. рис. 8.10). ►
Таким образом, для нахождения экстремумов функции требуется дополнительное исследование критических точек. Иными словами, требуется знать достаточное условие экстремума.
Первое достаточное условие экстремума
Теорема. Если при переходе через точку 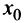 производная дифференцируемой функции
производная дифференцируемой функции  меняет свой знак с плюса на минус, то точка
меняет свой знак с плюса на минус, то точка 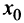 есть точка максимума функции
есть точка максимума функции 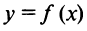 , а если с минуса на плюс, — то точка минимума.
, а если с минуса на плюс, — то точка минимума.
 Пусть производная меняет знак с плюса на минус, т.е. в некотором интервале
Пусть производная меняет знак с плюса на минус, т.е. в некотором интервале 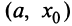 производная положительна
производная положительна 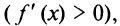 а в некотором интервале
а в некотором интервале 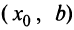 — отрицательна
— отрицательна 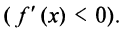 Тогда в соответствии с достаточным условием монотонности функция
Тогда в соответствии с достаточным условием монотонности функция 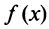 возрастает на интервале
возрастает на интервале 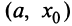 и убывает на интервале
и убывает на интервале 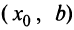 , (см. рис. 8.11).
, (см. рис. 8.11).
По определению возрастающей функции 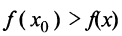 при всех
при всех 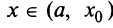 , а по определению убывающей функции
, а по определению убывающей функции 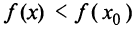 при всех
при всех 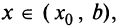 т.е.
т.е. 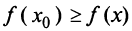 при всех
при всех 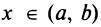 , следовательно,
, следовательно, 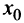 — точка максимума функции
— точка максимума функции  .
.
Аналогично рассматривается случай, когда производная меняет знак с минуса на плюс. ■
Отметим, что дифференцируемость функции в самой точке  не использовалась при доказательстве теоремы. На самом деле она и не требуется — достаточно, чтобы функция была непрерывна в точке
не использовалась при доказательстве теоремы. На самом деле она и не требуется — достаточно, чтобы функция была непрерывна в точке 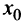 .
. 
Таким образом, достаточным условием существования экстремума функции 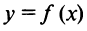 в точке
в точке 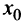 является изменение знака ее производной, т.е. углов наклона касательных к кривой
является изменение знака ее производной, т.е. углов наклона касательных к кривой 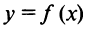 : с острых на тупые (рис. 8.12а) при переходе через точку максимума или с тупых на острые (рис. 8.126) при переходе через точку минимума. Если изменения знака производной не происходит, то экстремума нет.
: с острых на тупые (рис. 8.12а) при переходе через точку максимума или с тупых на острые (рис. 8.126) при переходе через точку минимума. Если изменения знака производной не происходит, то экстремума нет.
Схема исследования функции y=f(x) на экстремум:
Схема исследования функции 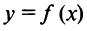 на экстремум:
на экстремум:
- Найти производную
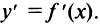
- Найти критические точки функции, в которых производная
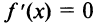 или не существует.
или не существует. - Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.
- Найти экстремумы (экстремальные значения) функции.
Пример №7
Исследовать на экстремум функцию 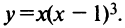
Решение:
1°. Производная функции 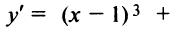
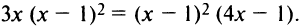
2°. Приравнивая производную к нулю, находим критические точки функции 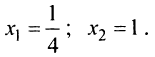 (Точек, в которых производная не существует, у данной функции нет —
(Точек, в которых производная не существует, у данной функции нет —  определена на всей числовой оси.)
определена на всей числовой оси.)
3°. Нанесем критические точки на числовую прямую (рис. 8.13).
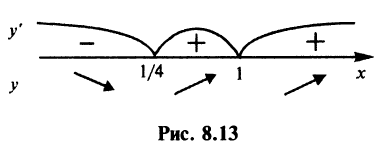
Для определения знака у производной слева и справа от критической точки 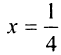 выберем, например, значения
выберем, например, значения 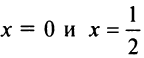 найдем
найдем
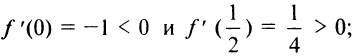 следовательно,
следовательно, 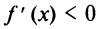 при всех
при всех
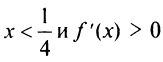 на интервале
на интервале 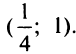
Аналогично устанавливаем, что 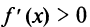 и на интервале
и на интервале 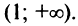 Согласно достаточному условию
Согласно достаточному условию 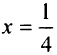 — точка минимума данной функции. В точке
— точка минимума данной функции. В точке 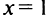 экстремума нет.
экстремума нет.
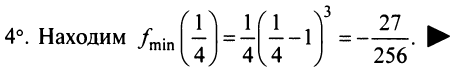
Второе достаточное условие экстремума
Теорема. Если первая производная 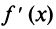 дважды дифференцируемой функции равна нулю в некоторой точке
дважды дифференцируемой функции равна нулю в некоторой точке 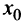 , а вторая производная в этой точке
, а вторая производная в этой точке 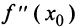 положительна, то
положительна, то 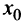 есть точка минимума функции
есть точка минимума функции 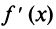 ; если
; если 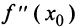 отрицательна, то
отрицательна, то 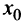 — точка максимума.
— точка максимума.
 Пусть
Пусть 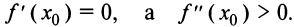 Это значит, что
Это значит, что 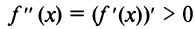 также и в некоторой окрестности точки
также и в некоторой окрестности точки 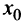 , т.е.
, т.е. 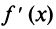 возрастает на некотором интервале
возрастает на некотором интервале 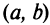 , содержащем точку
, содержащем точку 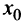 .
.
Но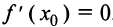 , следовательно, на интервале
, следовательно, на интервале 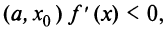 а на интервале
а на интервале 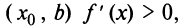 т.е.
т.е.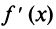 при переходе через точку х0 меняет знак с минуса на плюс, т.е.
при переходе через точку х0 меняет знак с минуса на плюс, т.е. 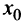 — точка минимума.
— точка минимума.
Аналогично рассматривается случай 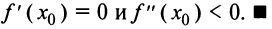
Схема исследования на экстремум функции 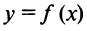 с помощью второго достаточного условия в целом аналогична схеме, приведенной выше (совпадают полностью пп. 1°, 2°, 4°). Отличие в п 3°, устанавливающем наличие экстремума: здесь необходимо найти вторую производную
с помощью второго достаточного условия в целом аналогична схеме, приведенной выше (совпадают полностью пп. 1°, 2°, 4°). Отличие в п 3°, устанавливающем наличие экстремума: здесь необходимо найти вторую производную 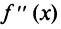 и определить ее знак в каждой критической точке.
и определить ее знак в каждой критической точке.
Пример №8
Производитель реализует свою продукцию по цене 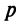 за единицу, а издержки при этом задаются кубической зависимостью
за единицу, а издержки при этом задаются кубической зависимостью 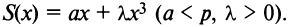 Найти оптимальный для производителя объем выпуска продукции и соответствующую ему прибыль.
Найти оптимальный для производителя объем выпуска продукции и соответствующую ему прибыль.
Решение:
Обозначим объем выпускаемой продукции 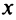 . Составим функцию прибыли
. Составим функцию прибыли 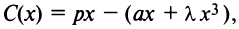 где
где 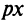 — доход от реализуемой продукции.
— доход от реализуемой продукции.
1°. Находим 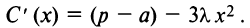
2°. Находим критические точки: 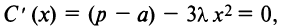 откуда
откуда 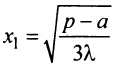 (вторую критическую точку
(вторую критическую точку 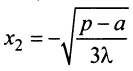 рассматриваем по смыслу задачи).
рассматриваем по смыслу задачи).
3°. Находим 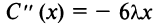 и определяем знак второй производной при
и определяем знак второй производной при 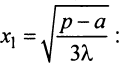
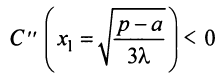 (в данном случае
(в данном случае 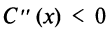 при любом
при любом 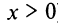 ), следовательно, при
), следовательно, при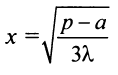 прибыль
прибыль 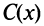 максимальна. 4°. Находим максимум функции (т.е. максимальный размер прибыли)
максимальна. 4°. Находим максимум функции (т.е. максимальный размер прибыли)
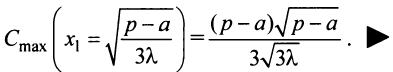
Второе достаточное условие экстремума утверждает, что если в критической точке 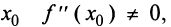 то в этой точке имеется экстремум. Обратное утверждение, однако, неверно. Экстремум в критической точке может быть и при равенстве в ней нулю второй производной.
то в этой точке имеется экстремум. Обратное утверждение, однако, неверно. Экстремум в критической точке может быть и при равенстве в ней нулю второй производной.
Рассмотрим, например, функцию 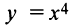 . Имеем
. Имеем 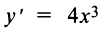 ,
, 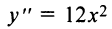 . В критической точке
. В критической точке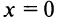 вторая производная также обращается в нуль. Но
вторая производная также обращается в нуль. Но 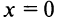 — точка экстремума, а именно — минимума. Так что в отличие от первого второе достаточное условие является именно только достаточным, но не необходимым. Поэтому, если в критической точке
— точка экстремума, а именно — минимума. Так что в отличие от первого второе достаточное условие является именно только достаточным, но не необходимым. Поэтому, если в критической точке 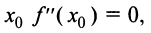 то рекомендуется перейти к первому достаточному условию экстремума.
то рекомендуется перейти к первому достаточному условию экстремума.
Наибольшее и наименьшее значения функции на отрезке
При решении прикладных задач, в частности оптимизационных, важное значение имеют задачи на нахождение наибольшего и наименьшего значений {глобального максимума и глобального минимума) функции на промежутке X.
Согласно теореме Вейерштрасса (§ 6.7), если функция 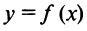 непрерывна на отрезке
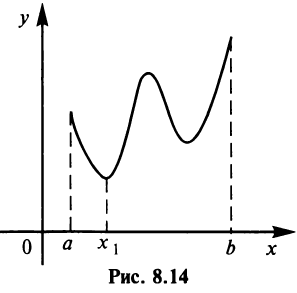
непрерывна на отрезке 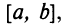 то она принимает на нем наибольшее и наименьшее значения. Наибольшее или наименьшее значение функции может достигаться как в точках экстремума, так и в точках на концах отрезка. Так, на рис. 8.14 наибольшее значение функции на конце отрезка
то она принимает на нем наибольшее и наименьшее значения. Наибольшее или наименьшее значение функции может достигаться как в точках экстремума, так и в точках на концах отрезка. Так, на рис. 8.14 наибольшее значение функции на конце отрезка 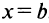 , а наименьшее — в точке минимума
, а наименьшее — в точке минимума 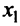 .
. 
Для отыскания наибольшего и наименьшего значений на отрезке рекомендуется пользоваться следующей схемой:
1°. Найти производную 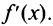
2°. Найти критические точки функции, в которых 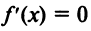 или не существует.
или не существует.
3°. Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее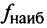 и наименьшее
и наименьшее 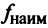 .
.
Пример №9
Найти наибольшее и наименьшее значения функции 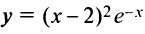 на отрезке
на отрезке 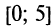 .
.
Решение:
1°.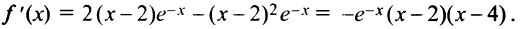
2°. 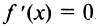 , откуда критические точки
, откуда критические точки 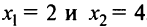 .
.
3°. Значения функции в критических точках 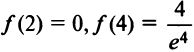 и на концах отрезка
и на концах отрезка 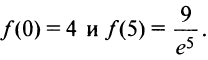 Итак,
Итак,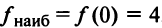 ,
,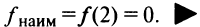
Замечание. Если функция 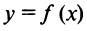 непрерывна на интервале
непрерывна на интервале 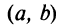 , то она может не принимать на нем наибольшее и наименьшее значения. В частном случае, если дифференцируемая функция на интервале
, то она может не принимать на нем наибольшее и наименьшее значения. В частном случае, если дифференцируемая функция на интервале 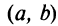 имеет лишь одну точку максимума (или одну точку минимума), то наибольшее (или наименьшее) значение функции совпадает с максимумом (или минимумом) этой функции. Например, на интервале
имеет лишь одну точку максимума (или одну точку минимума), то наибольшее (или наименьшее) значение функции совпадает с максимумом (или минимумом) этой функции. Например, на интервале 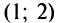 функция
функция 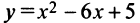 имеет один минимум
имеет один минимум 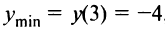 , следовательно, это и есть наименьшее значение функции
, следовательно, это и есть наименьшее значение функции 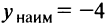 . Заметим, что наибольшего значения данная функция на указанном интервале не имеет.
. Заметим, что наибольшего значения данная функция на указанном интервале не имеет.
Выпуклость функции. Точки перегиба
Ранее мы подробно изучали точки экстремума, нахождение которых во многом определяет структуру графика функции. Определим теперь другие «узловые» точки функции, которые также следует найти, чтобы качественно построить ее график.
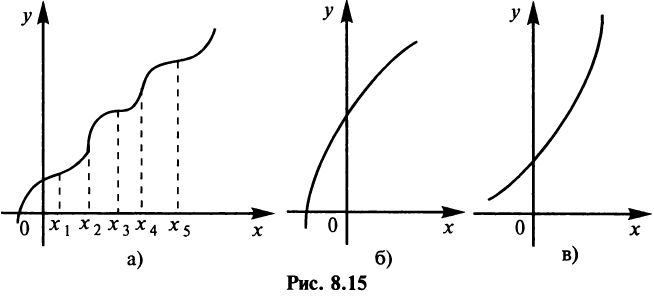
Рассмотрим функцию, график которой изображен на рис. 8.15а. Эта функция возрастает на всей числовой оси и не имеет экстремумов. Очевидно, однако, ее отличие от функций, изображенных на рис. 8.156 и 8.15в. В точках 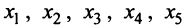 график как бы «перегибается». Поэтому такие точки называются точками перегиба, к строгому определению которых мы и переходим.
график как бы «перегибается». Поэтому такие точки называются точками перегиба, к строгому определению которых мы и переходим.
Прежде всего определим различие поведения функции по разные стороны от точек 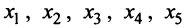
Определение 1. Функция 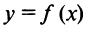 называется выпуклой вниз на промежутке X, если для любых двух значений
называется выпуклой вниз на промежутке X, если для любых двух значений 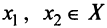 из этого промежутка выполняется неравенство
из этого промежутка выполняется неравенство 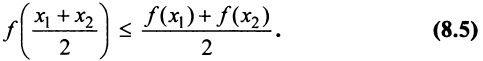
Определение 2. Функция называется выпуклой вверх на промежутке X, если для любых двух значений 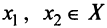 из этого промежутка выполняется неравенство
из этого промежутка выполняется неравенство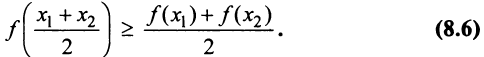
Графики функций, выпуклых вниз и вверх, изображены на рис. 8.16. Очевидно, что если функция выпукла вниз, то отрезок, соединяющий любые две точки графика, целиком лежит над графиком (см. рис. 8.16а), если — выпукла вверх, то весь такой отрезок целиком лежит под графиком функции (см. рис. 8.166). 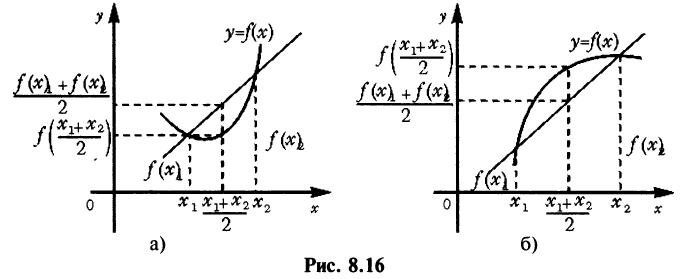
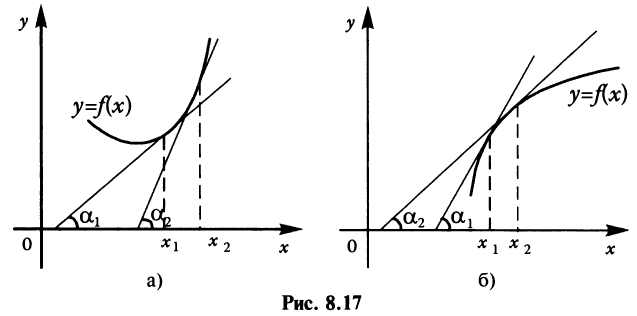
Теорема. Функция выпукла вниз (вверх) на промежутке X тогда и только тогда, когда ее первая производная на этом промежутке монотонно возрастает (убывает).
Геометрический смысл теоремы состоит в том, что если 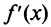 возрастает (убывает) на промежутке X, то возрастает (убывает) угол наклона касательных к графику (см. рис. 8.17а, б). Это и означает выпуклость функции вниз (вверх).
возрастает (убывает) на промежутке X, то возрастает (убывает) угол наклона касательных к графику (см. рис. 8.17а, б). Это и означает выпуклость функции вниз (вверх).
Используя условия монотонности, мы можем определить следующее достаточное условие выпуклости функции вниз (вверх).
Теорема. Если вторая производная дважды дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка X, то функция выпукла вниз (вверх) на этом промежутке.
Если 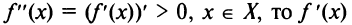 , возрастает на промежутке X, следовательно, на основании предыдущей теоремы функция выпукла вниз на промежутке X. Аналогично рассматривается случай
, возрастает на промежутке X, следовательно, на основании предыдущей теоремы функция выпукла вниз на промежутке X. Аналогично рассматривается случай 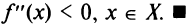
Необходимое условие выпуклости слабее: если функция выпукла на промежутке X, то можно утверждать лишь, что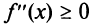 (или
(или 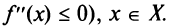 Например, функция
Например, функция 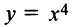 выпукла на всей
выпукла на всей
числовой оси, хотя вторая производная 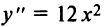 не всюду положительна: при
не всюду положительна: при 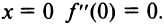
Определение. Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла вниз и вверх.
Из вышесказанного следует, что точки перегиба — это точки экстремума первой производной. Отсюда вытекают следующие утверждения.
Теорема (необходимое условие перегиба). Вторая производная 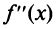 дважды дифференцируемой функции в точке перегиба
дважды дифференцируемой функции в точке перегиба 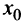 равна нулю, т.е.
равна нулю, т.е.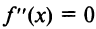 .
.
Теорема (достаточное условие перегиба). Если вторая производная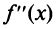 дважды дифференцируемой функции при переходе через некоторую точку
дважды дифференцируемой функции при переходе через некоторую точку 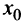 меняет свой знак, то
меняет свой знак, то 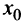 есть точка перегиба ее графика.
есть точка перегиба ее графика.
Нужно иметь в виду следующую геометрическую интерпретацию точек перегиба (см. рис. 8.18).
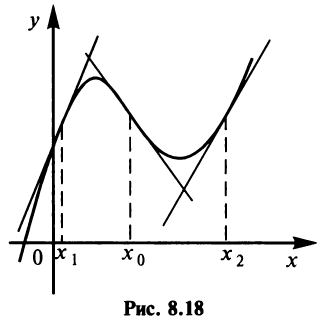
В окрестности точки 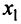 функция выпукла вверх и график ее лежит ниже касательной, проведенной в этой точке. В окрестности точки
функция выпукла вверх и график ее лежит ниже касательной, проведенной в этой точке. В окрестности точки 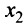 , на которой функция выпукла вниз, картина обратная — график лежит выше касательной. В точке же перегиба
, на которой функция выпукла вниз, картина обратная — график лежит выше касательной. В точке же перегиба 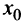 касательная разделяет график — он лежит по разные стороны касательной.
касательная разделяет график — он лежит по разные стороны касательной.
Следует отметить, что если критическая точка дифференцируемой функции не является точкой экстремума, то она есть точка перегиба.
Схема исследования функции на выпуклость и точки перегиба
Схема исследования функции на выпуклость и точки перегиба:
1°. Найти вторую производную функции 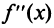 .
.
2°. Найти точки, в которых вторая производная 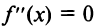 или не существует.
или не существует.
3°. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости и наличии точек перегиба.
4°. Найти значения функции в точках перегиба.
Пример №10
Найти интервалы выпуклости и точки перегиба графика функции 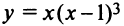 .
.
Решение:
1°. 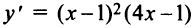 (см. пример 8.7). 2°.
(см. пример 8.7). 2°. 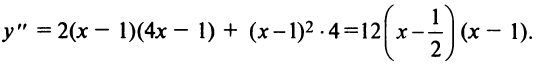
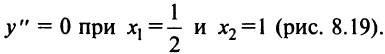
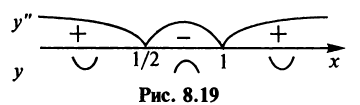 3°.
3°. 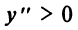 на интервалах
на интервалах 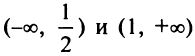 , следовательно, на этих интервалах функция выпукла вниз;
, следовательно, на этих интервалах функция выпукла вниз;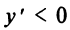 на интервале
на интервале 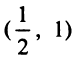 , следовательно, функция на нем выпукла вверх, а
, следовательно, функция на нем выпукла вверх, а 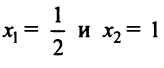 есть точки перегиба.
есть точки перегиба.
4°. Значения функции в точках перегиба 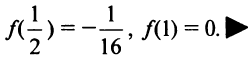
Асимптоты графика функции
В предыдущих параграфах мы изучали характерные точки функции. Теперь рассмотрим характерные линии. Важнейшими из них являются асимптоты.
Определение. Асимптотой графика функции 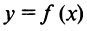 называется прямая, обладающая тем свойством, что расстояние от точки
называется прямая, обладающая тем свойством, что расстояние от точки 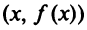 до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
На рис. 8.20а изображена вертикальная асимптота, на рис. 8.206 — горизонтальная асимптота, а на рис. 8.20в — наклонная. Очевидно, этими тремя случаями исчерпываются все возможные расположения асимптот. 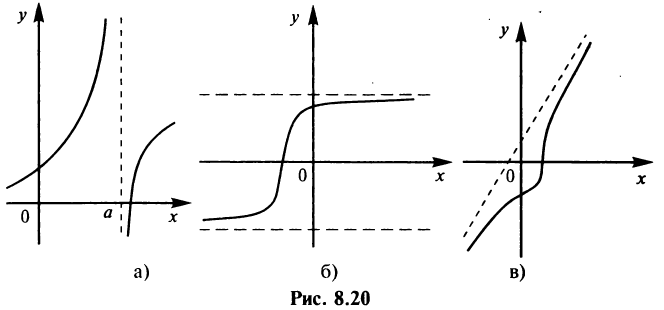
Нахождение асимптот графика основано на следующих утверждениях.
Теорема 1. Пусть функция 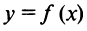 определена в некоторой окрестности точки
определена в некоторой окрестности точки 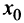 (исключая, возможно, саму эту точку) и хотя бы один из пределов функции при
(исключая, возможно, саму эту точку) и хотя бы один из пределов функции при 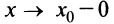 (слева) или при
(слева) или при 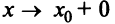
(справа) равен бесконечности, т.е. 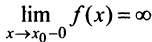 или
или 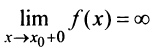 Тогда прямая
Тогда прямая 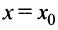 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции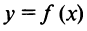 .
.
Очевидно, что прямая 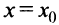 не может быть вертикальной асимптотой, если функция непрерывна в точке
не может быть вертикальной асимптотой, если функция непрерывна в точке 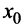 , так как в этом случае
, так как в этом случае 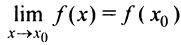 . Следовательно, вертикальные асимптоты
. Следовательно, вертикальные асимптоты 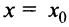 следует искать в точках разрыва функции
следует искать в точках разрыва функции 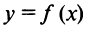 или на концах ее области определения
или на концах ее области определения 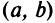 , если
, если 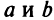 — конечные числа.
— конечные числа.
Теорема 2. Пусть функция 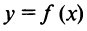 определена при достаточно больших
определена при достаточно больших 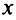 и существует конечный предел функции
и существует конечный предел функции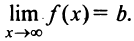 Тогда прямая
Тогда прямая 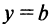 есть горизонтальная асимптота графика функции
есть горизонтальная асимптота графика функции 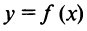 .
.
Замечание. Если конечен только один из пределов
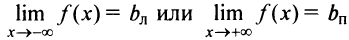 , то функция имеет лишь левостороннюю
, то функция имеет лишь левостороннюю 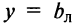 или правостороннюю
или правостороннюю 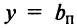 горизонтальную асимптоту.
горизонтальную асимптоту.
В том случае, если 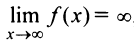 , функция может иметь наклонную асимптоту.
, функция может иметь наклонную асимптоту.
Теорема 3. Пусть функция 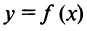 определена при достаточно больших
определена при достаточно больших 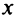 и существуют конечные пределы
и существуют конечные пределы 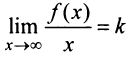 и
и 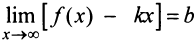 . Тогда прямая
. Тогда прямая 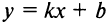 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции 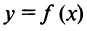 .
.
 Если
Если 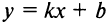 — наклонная асимптота, то очевидно, что
— наклонная асимптота, то очевидно, что 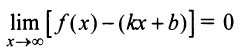 и тем более
и тем более 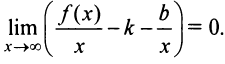 Поэтому
Поэтому 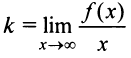 . Теперь из равенства
. Теперь из равенства 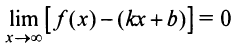 , учитывая, что
, учитывая, что 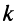 — конечное число, получаем:
— конечное число, получаем: 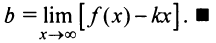
Наклонная асимптота, так же как и горизонтальная, может быть правосторонней или левосторонней.
Пример №11
Найти асимптоты графика дробно-линейной функции 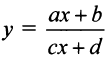 где
где 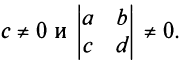
Решение:
Из области определения выпадает точка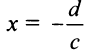 . Найдем пределы функции
. Найдем пределы функции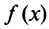 при
при 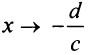 .
.
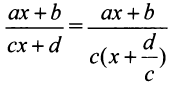 В силу того, что
В силу того, что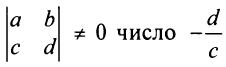 не является корнем числителя, т.е. при
не является корнем числителя, т.е. при 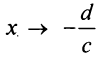 числитель не стремится к нулю. Отсюда
числитель не стремится к нулю. Отсюда 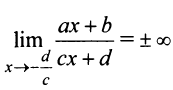 и прямая и
и прямая и 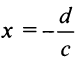 является вертикальной асимптотой. Далее
является вертикальной асимптотой. Далее 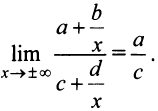
Отсюда следует, что прямая 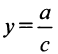 является горизонтальной асимптотой. (Заметим, что ранее в § 4.5 уравнения асимптот дробно-линейной функции были найдены путем параллельного переноса осей координат в центр ее графика — равносторонней гиперболы.)
является горизонтальной асимптотой. (Заметим, что ранее в § 4.5 уравнения асимптот дробно-линейной функции были найдены путем параллельного переноса осей координат в центр ее графика — равносторонней гиперболы.)
Так, например, асимптотами функции 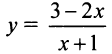 являются прямые
являются прямые 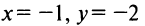 (график функции приведен на рис. 4.24). ►
(график функции приведен на рис. 4.24). ►
Пример №12
Найти асимптоты графика функции 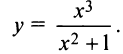
Решение:
Очевидно, график функции не имеет ни вертикальных асимптот (нет точек разрыва), ни горизонтальных Найдем наклонную асимптоту.
Найдем наклонную асимптоту.
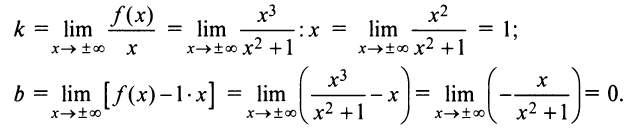
Таким образом, наклонная асимптота графика функции имеет вид 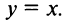 ►
►
Общая схема исследования функций и построения их графиков
При исследовании функций и построении их графиков рекомендуется использовать следующую схему.
- Найти область определения функции.
- Исследовать функцию на четность—нечетность.
- Найти вертикальные асимптоты.
- Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.
- Найти экстремумы и интервалы монотонности функции.
- Найти интервалы выпуклости функции и точки перегиба.
- Найти точки пересечения графика с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.
Заметим, что исследование функции проводится одновременно с построением ее графика.
Пример №13
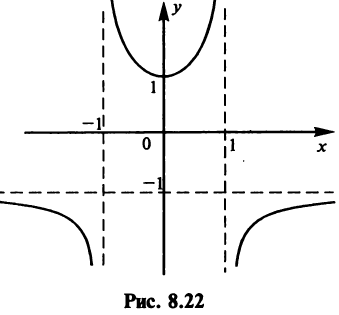
Исследовать функцию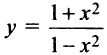 построить ее график.
построить ее график.
Решение:
1°. Область определения 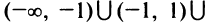
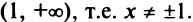
2°.Функция четная, так как 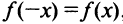 , и ее график симметричен относительно оси ординат.
, и ее график симметричен относительно оси ординат.
3°. Вертикальные асимптоты могут пересекать ось абсцисс в точках 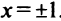 . Так как пределы функции при
. Так как пределы функции при 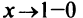 (слева) и при
(слева) и при 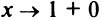 (справа) бесконечны, т.е.
(справа) бесконечны, т.е.
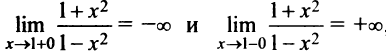 то прямая
то прямая  есть вертикальная асимптота. В силу симметрии графика
есть вертикальная асимптота. В силу симметрии графика 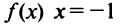 также вертикальная асимптота.
также вертикальная асимптота.
4°. Поведение функции в бесконечности. Вычислим 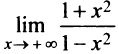
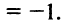
В силу четности имеем также 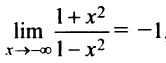 , т.е. прямая
, т.е. прямая 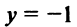 — горизонтальная асимптота.
— горизонтальная асимптота.
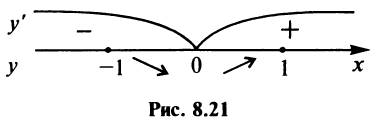
5°. Экстремумы и интервалы монотонности.
Найдем 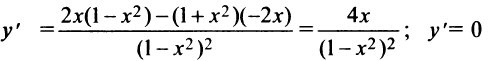 при
при 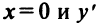 не существует при
не существует при 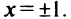
Однако критической является только точка 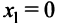 (так как значения
(так как значения 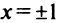 не входят в область определения функции). Поскольку
не входят в область определения функции). Поскольку 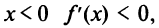 а при
а при 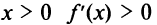 (рис. 8.21), то
(рис. 8.21), то 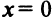 — точка минимума и
— точка минимума и 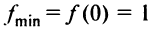 — минимум функции. На интервалах
— минимум функции. На интервалах 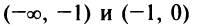 функция убывает, на интервалах
функция убывает, на интервалах 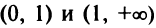 — возрастает.
— возрастает.
6°. Интервалы выпуклости и точки перегиба. Найдем
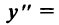
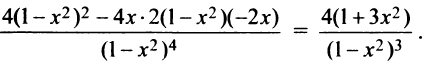
Очевидно, что 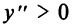 на интервале
на интервале 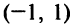 и функция выпукла вниз на этом интервале.
и функция выпукла вниз на этом интервале. 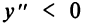 на интервалах
на интервалах 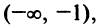
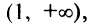 и на этих интервалах функция выпукла вверх. Точек перегиба нет.
и на этих интервалах функция выпукла вверх. Точек перегиба нет.
7°. Точки пересечения с осями.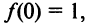 т.е. точка пересечения с осью ординат
т.е. точка пересечения с осью ординат 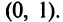 Уравнение
Уравнение 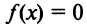 решений не имеет, следовательно, график функции не пересекает ось абсцисс. График функции изображен на рис. 8.22. ►
решений не имеет, следовательно, график функции не пересекает ось абсцисс. График функции изображен на рис. 8.22. ►
Пример №14
Исследовать функцию 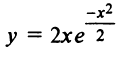 и построить ее график.
и построить ее график.
Решение:
1°. Область определения 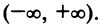
2°.Функция нечетная, так как 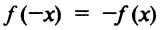 и график ее симметричен относительно начала координат.
и график ее симметричен относительно начала координат.
3°. Вертикальных асимптот нет, так как функция определена при всех действительных значениях 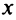 .
.
4°. Поведение функции в бесконечности: 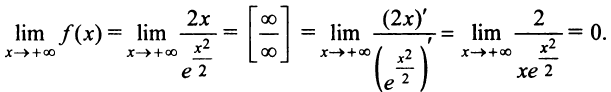 В силу нечетности функции
В силу нечетности функции 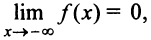 , т.е. прямая
, т.е. прямая 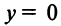 (ось абсцисс) — горизонтальная асимптота.
(ось абсцисс) — горизонтальная асимптота.
5°. Экстремумы и интервалы монотонности:
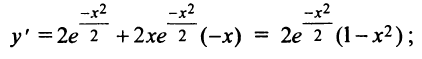
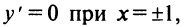 т.е. критические точки
т.е. критические точки 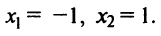 Знаки производной изображены на рис. 8.23.
Знаки производной изображены на рис. 8.23.
Таким образом, 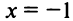 есть точка минимума;
есть точка минимума; 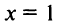 — точка максимума и
— точка максимума и

Функция убывает на интервалах 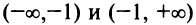 и возрастает на интервале
и возрастает на интервале 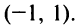
6°. Интервалы выпуклости и точки перегиба:
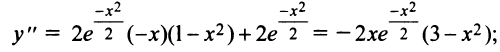
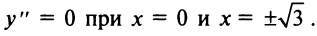 Знаки второй производной изображены на рис. 8.24.
Знаки второй производной изображены на рис. 8.24.
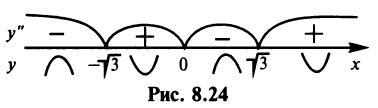
Таким образом, функция выпукла вниз на интервалах 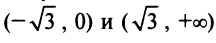 и
и 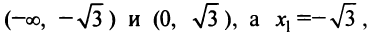 и выпукла вверх на интервалах
и выпукла вверх на интервалах
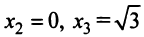 — точки перегиба.
— точки перегиба.
7°. 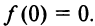 Уравнение
Уравнение 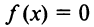 имеет единственное решение
имеет единственное решение 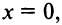 т.е. график функции пересекает оси в начале координат
т.е. график функции пересекает оси в начале координат 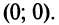 График функции изображен на рис. 8.25. ►
График функции изображен на рис. 8.25. ►
Пример №15
Найти пределы:
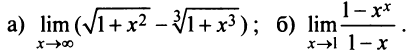
Решение:
а) Имеем неопределенность вида 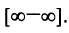 Вынося
Вынося 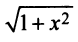 , придем к неопределенности вида
, придем к неопределенности вида 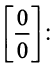
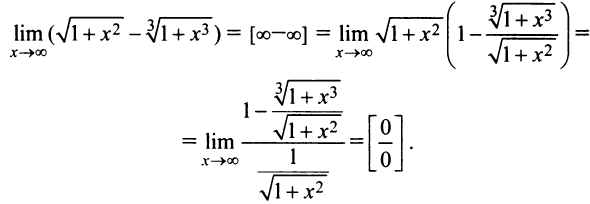
Далее применим правило Лопиталя:
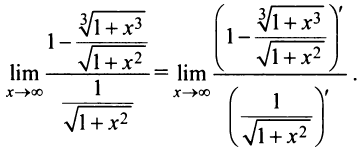
После преобразования (рекомендуем их провести читателю) получим
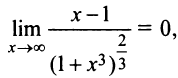
так как степень старшего члена числителя (единица) ниже степени знаменателя (равного двум).
б) Имеем неопределенность вида 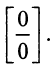 Применим правило Лопиталя:
Применим правило Лопиталя:
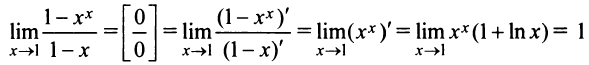
Пример №16
Капитал в 1 млрд. рублей может быть размешен в банке под 50% годовых или инвестирован в производство, причем эффективность вложения ожидается в размере 100%, а издержки задаются квадратичной зависимостью. Прибыль облагается налогом в 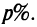 При каких значениях
При каких значениях 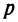 вложение в производство является более эффективным, нежели чистое размещение капитала в банке?
вложение в производство является более эффективным, нежели чистое размещение капитала в банке?
Решение:
Пусть 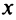 (млрд. рублей) инвестируется в производство, а
(млрд. рублей) инвестируется в производство, а 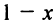 — размещается под проценты. Тогда размещенный капитал через год станет равным
— размещается под проценты. Тогда размещенный капитал через год станет равным 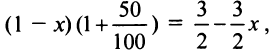 а капитал, вложенный в производство:
а капитал, вложенный в производство: 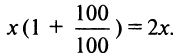 Издержки составят
Издержки составят 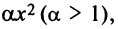 , т.е. прибыль от вложения в производство
, т.е. прибыль от вложения в производство 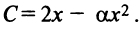 Налоги составят
Налоги составят 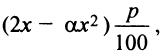 т.е. чистая прибыль окажется равной
т.е. чистая прибыль окажется равной 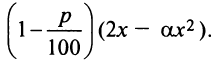
Общая сумма через год составит:
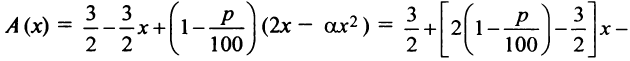
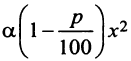 , и требуется найти максимальное значение этой функции на отрезке
, и требуется найти максимальное значение этой функции на отрезке 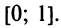 Имеем
Имеем
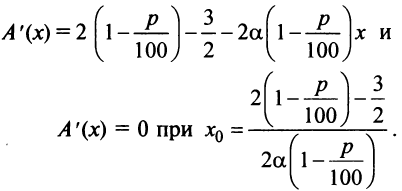
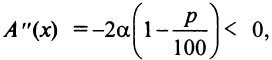 т.е. согласно второму достаточному условию экстремума
т.е. согласно второму достаточному условию экстремума 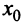 — точка максимума.
— точка максимума.
Чтобы 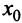 принадлежало отрезку
принадлежало отрезку 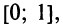 необходимо выполнение условия
необходимо выполнение условия
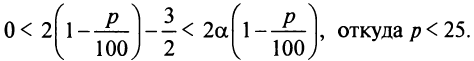
Таким образом, если 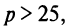 то выгоднее ничего не вкладывать в производство и разместить весь капитал в банк. Если
то выгоднее ничего не вкладывать в производство и разместить весь капитал в банк. Если 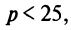 то можно показать, что при
то можно показать, что при 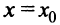
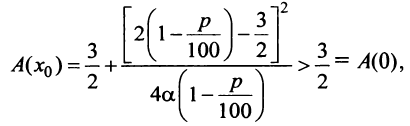
т.е. вложение в производство является более выгодным, чем чистое размещение под проценты. ►
Пример №17
Исследовать функцию 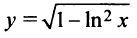 и построить ее график.
и построить ее график.
Решение:
1°. Область определения функции задается системой
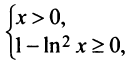
решение которой отрезок 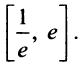
2°.Функция общего вида — ни четная, ни нечетная.
3°.Вертикальные асимптоты. Функция непрерывна на всей области определения. Граничными точками области определения являются точки 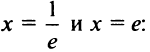
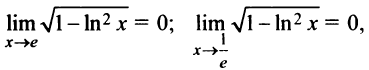 т.е. вертикальных асимптот нет.
т.е. вертикальных асимптот нет.
4°. Поведение функции в бесконечности. Так как функция не определена при 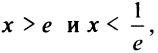 понятие горизонтальной или наклонной асимптоты для нее не имеет смысла.
понятие горизонтальной или наклонной асимптоты для нее не имеет смысла.
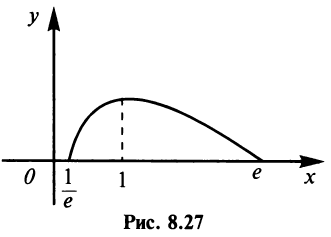
5°. Экстремумы и интервалы монотонности.
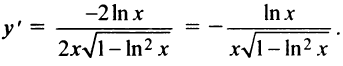
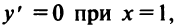 т.е. критическая точка
т.е. критическая точка 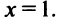 Заметим, что на интервале
Заметим, что на интервале 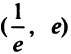 это единственная критическая точка.Знаки производной указаны на рис. 8.26.
это единственная критическая точка.Знаки производной указаны на рис. 8.26.
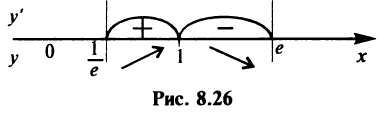
Таким образом, 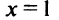 — точка максимума функции и
— точка максимума функции и 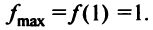
6°. Интервалы выпуклости и точки перегиба. Получим после преобразований (рекомендуется читателю найти самостоятельно)
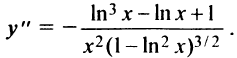
Очевидно, что при 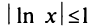 величина
величина 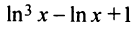 положительна, т.е.
положительна, т.е. 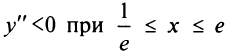 и функция выпукла вверх на всей области определения. Точек перегиба нет. График функции изображена рис. 8.27. ►
и функция выпукла вверх на всей области определения. Точек перегиба нет. График функции изображена рис. 8.27. ►
Пример №18
Исследовать функцию 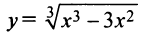 и построить ее график.
и построить ее график.
Решение:
1°. Область определения — 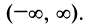
2°. Функция общего вида (ни четная, ни нечетная), так как 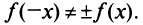
3°. Вертикальных асимптот нет, так как функция определена и непрерывна на всем множестве действительных чисел.
4°. Поведение функции в бесконечности:
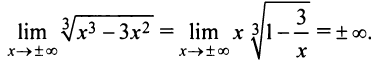
Следовательно, горизонтальных асимптот функция не имеет. Найдем наклонные асимптоты: 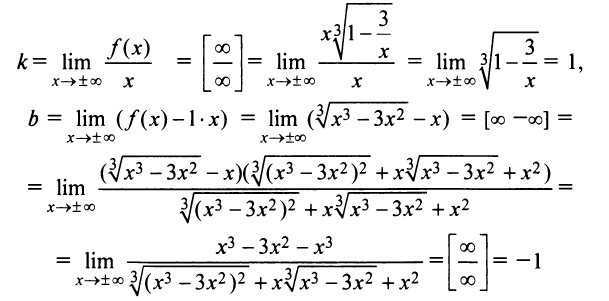
(так как после упрощения в числителе старший член 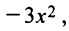 в знаменателе фактически
в знаменателе фактически 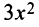 ).
). 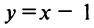 есть наклонная асимптота.
есть наклонная асимптота.
5°. Экстремумы и интервалы монотонности: 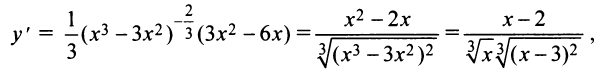
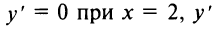 — не существует при
— не существует при 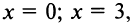 т.е. критические точки
т.е. критические точки 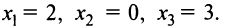 Знаки производной указаны на рис. 8.28.
Знаки производной указаны на рис. 8.28.
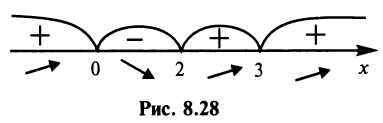
Таким образом, 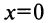 — точка максимума и
— точка максимума и 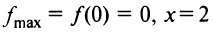 — точка минимума и
— точка минимума и 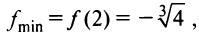 не является точкой экстремума.
не является точкой экстремума.
6°. Интервалы выпуклости и точки перегиба. После преобразований получим
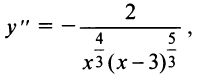
т.е. 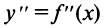 нигде не обращается в нуль и не существует в точках
нигде не обращается в нуль и не существует в точках 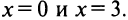 Знаки
Знаки 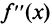 указаны на рис. 8.29. Таким образом, интервалы выпуклости вниз
указаны на рис. 8.29. Таким образом, интервалы выпуклости вниз 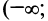
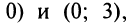 интервал выпуклости вверх
интервал выпуклости вверх 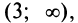 а
а 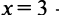 — точка перегиба.
— точка перегиба.
7°. Точки пересечения с осями. 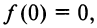 следовательно, ось ординат пересекает график в точке
следовательно, ось ординат пересекает график в точке 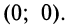 Уравнение
Уравнение 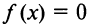 имеет два решения
имеет два решения 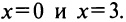 Следовательно, график пересекает ось абсцисс в двух точках
Следовательно, график пересекает ось абсцисс в двух точках 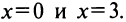 График функции изображен на рис. 8.30.
График функции изображен на рис. 8.30.
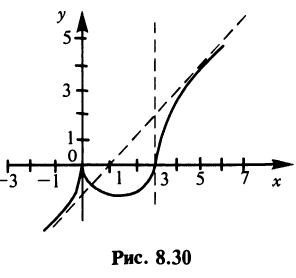
Обратим внимание на то, что в точке экстремума 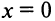 и в точке перегиба х = 3 соответственно первая и вторая производные не обращаются в нуль — они не существуют в этих точках. ►
и в точке перегиба х = 3 соответственно первая и вторая производные не обращаются в нуль — они не существуют в этих точках. ►
Приложение производной в экономической теории
Рассмотрим некоторые примеры приложения производной в экономической теории. Как мы увидим, многие, в том числе базовые, законы теории производства и потребления, спроса и предложения оказываются прямыми следствиями математических теорем, сформулированных в настоящей главе.
Вначале рассмотрим экономическую интерпретацию теоремы Ферма.
Один из базовых законов теории производства звучит так: оптимальный для производителя уровень выпуска товара определяется равенством предельных издержек и предельного дохода.
То есть уровень выпуска 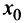 является оптимальным для производителя, если
является оптимальным для производителя, если 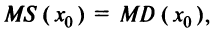 где
где 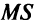 — предельные издержки, a
— предельные издержки, a 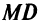 — предельный доход.
— предельный доход.
Обозначим функцию прибыли за 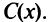 Тогда
Тогда 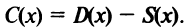 Очевидно, что оптимальным уровнем производства является тот, при котором прибыль максимальна, т.е. такое значение выпуска
Очевидно, что оптимальным уровнем производства является тот, при котором прибыль максимальна, т.е. такое значение выпуска 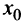 , при котором функция
, при котором функция 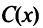 имеет экстремум (максимум). По теореме Ферма в этой точке
имеет экстремум (максимум). По теореме Ферма в этой точке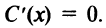 Но
Но 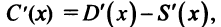 поэтому
поэтому 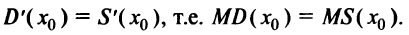
Другое важное понятие теории производства — это уровень наиболее экономичного производства, при котором средние издержки по производству товара минимальны. Соответствующий экономический закон гласит: уровень наиболее экономичного производства определяется равенством средних и предельных издержек. Получим это утверждение как следствие теоремы Ферма.
Средние издержки 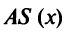 определяются как
определяются как 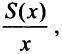 т.е. издержки по производству товара, деленные на произведенное его количество. Минимум этой величины достигается в критической точке функции
т.е. издержки по производству товара, деленные на произведенное его количество. Минимум этой величины достигается в критической точке функции 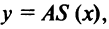 т.е. при условии
т.е. при условии
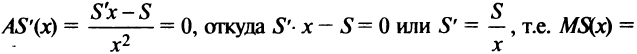
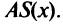
Понятие выпуклости функции также находит свою интерпретацию в экономической теории.
Один из наиболее знаменитых экономических законов — закон убывающей доходности — звучит следующим образом: с увеличением производства дополнительная продукция, полученная на каждую новую единицу ресурса (трудового, технологического и т.д.), с некоторого момента убывает.
Иными словами, величина 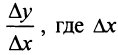 — приращение ресурса, а
— приращение ресурса, а 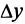 — приращение выпуска продукции, уменьшается при увеличении
— приращение выпуска продукции, уменьшается при увеличении 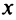 . Таким образом, закон убывающей доходности формулируется так: функция
. Таким образом, закон убывающей доходности формулируется так: функция 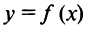 ,выражающая зависимость выпуска продукции от вложенного ресурса, является функцией, выпуклой вверх.
,выражающая зависимость выпуска продукции от вложенного ресурса, является функцией, выпуклой вверх.
Другим базисным понятием экономической теории является функция полезности 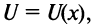 где
где 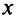 — количество товара, a
— количество товара, a 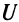 — полезность. Эта величина очень субъективная для каждого отдельного потребителя, но достаточно объективная для общества в целом. Закон убывающей полезности звучит следующим образом: с ростом количества товара дополнительная полезность от каждой новой его единицы с некоторого момента убывает. Очевидно, этот закон можно переформулировать так: функция полезности является функцией, выпуклой вверх. В такой постановке закон убывающей полезности служит отправной точкой для математического исследования теории спроса и предложения.
— полезность. Эта величина очень субъективная для каждого отдельного потребителя, но достаточно объективная для общества в целом. Закон убывающей полезности звучит следующим образом: с ростом количества товара дополнительная полезность от каждой новой его единицы с некоторого момента убывает. Очевидно, этот закон можно переформулировать так: функция полезности является функцией, выпуклой вверх. В такой постановке закон убывающей полезности служит отправной точкой для математического исследования теории спроса и предложения.
Правило Лопиталя (раскрытие неопределенностей 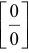 и
и  )
)
Пусть функции 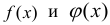 на некотором отрезке
на некотором отрезке 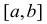 удовлетворяют условиям теоремы Коши и обращаются в нуль в точке х = с этого отрезка, т.е.
удовлетворяют условиям теоремы Коши и обращаются в нуль в точке х = с этого отрезка, т.е. 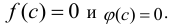
Отношение 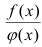 не определено при х = с, но имеет вполне определенный смысл при значении
не определено при х = с, но имеет вполне определенный смысл при значении 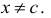 Следовательно, может быть поставлен вопрос о разыскании предела этого отношения при
Следовательно, может быть поставлен вопрос о разыскании предела этого отношения при 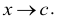 Вычисление пределов такого типа называется обычно «раскрытием неопределенностей вида
Вычисление пределов такого типа называется обычно «раскрытием неопределенностей вида 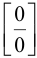 ».
».
Неопределенная ситуация складывается также, если 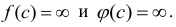 В этом случае для вычисления предела отношения
В этом случае для вычисления предела отношения 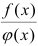 при
при 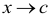 называется
называется
«раскрытием неопределенностей вида 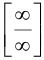 ».
».
Правило Лопиталя. Пусть функции 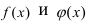 на некотором отрезке
на некотором отрезке 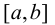 удовлетворяют условиям теоремы Коши и обращаются в нуль или бесконечность х = с этого отрезка, тогда вычисление предела отношения этих функций при
удовлетворяют условиям теоремы Коши и обращаются в нуль или бесконечность х = с этого отрезка, тогда вычисление предела отношения этих функций при 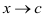 можно заменить вычислением предела отношения их производных
можно заменить вычислением предела отношения их производных
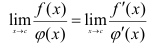
Замечание. Следует избегать распространенной ошибки, когда правая часть читается не как отношение производных, а как производная частного.
Следствие. Если отношение 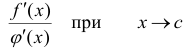 вновь приводит к
вновь приводит к
неопределенностям типа 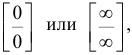 то следует повторно воспользоваться
то следует повторно воспользоваться
правилом Лопиталя и т.д. Таким образом, вычисление предела может при повторных появлениях неопределенностей тех же типов выглядеть так:
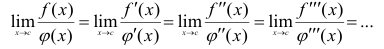
Замена отношения производных на отношение производных более высокого порядка продолжается до тех пор, пока не исчезнет неопределенность.
Пример №19
Найти предел 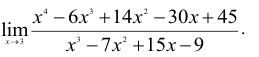
Решение:
Имеем неопределенность типа 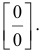 Воспользуемся правилом Лопиталя
Воспользуемся правилом Лопиталя
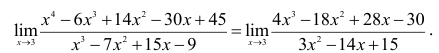
Вновь получаем неопределенность типа 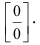 Продолжаем использование правила Лопиталя
Продолжаем использование правила Лопиталя 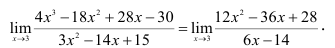
Подставляя значение х = 3, получаем
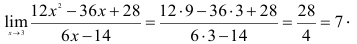
Ответ: 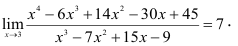
Пример №20
Найти предел функции 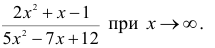
Решение:
В примере встретилась неопределенность 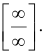
Для нахождения предела воспользуемся дважды правилом Лопиталя :
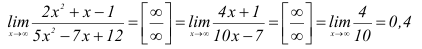
Ответ: 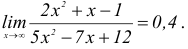
Применение дифференциального исчисления к исследованию функций
При изучении различных экономических процессов практически всегда удается установить функциональную связь между величинами или параметрами, характеризующими исследуемые процессы. Эта функциональная зависимость выражается аналитически в виде одной или нескольких формул. Одно из самых важных назначений дифференциального исчисления - это применение его к исследованию функций, т.е. к характеристике поведения функции при изменении независимой переменной.
Возрастание и убывание функции
Определение 1. Функция f(х) называется возрастающей в точке 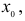 если в некоторой
если в некоторой 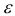 -окрестности этой точки
-окрестности этой точки 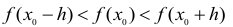 при любом положительном
при любом положительном 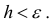
Определение 2. Функция f(х) называется возрастающей на отрезке 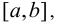 если для любых
если для любых 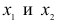 на этом отрезке
на этом отрезке 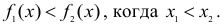
Аналогично определяется убывание функции в точке и на отрезке.
Теорема. 1) Если функция f(х), имеющая производную на отрезке
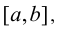 возрастает на этом отрезке, то её производная на отрезке
возрастает на этом отрезке, то её производная на отрезке 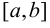 не отрицательна, т.е.
не отрицательна, т.е.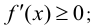
2) если функция f(х) непрерывна на отрезке 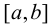 и дифференцируема
и дифференцируема
в промежутке 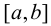 , причем
, причем 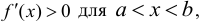 то эта функция возрастает на отрезке
то эта функция возрастает на отрезке 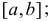
3) если функция f(х) непрерывна на отрезке 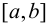 не изменяется (есть константа), то производная f'(х) = 0.
не изменяется (есть константа), то производная f'(х) = 0.
Доказательство. Докажем сначала первую часть теоремы
Пусть f(х) возрастает на отрезке 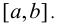 Придадим аргументу приращение и рассмотрим отношение
Придадим аргументу приращение и рассмотрим отношение 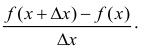
Так как f(х) возрастающая, то
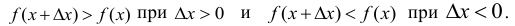
В обоих случаях знаки числителя и знаменателя рассматриваемого отношения одинаковы, следовательно, в обоих случаях 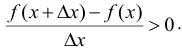 В итоге
В итоге
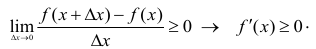
Докажем вторую часть теоремы.
Пусть f'(х)>0 при всех значениях х, принадлежащих промежутку 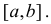
Рассмотрим два любых значения 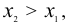 принадлежащих промежутку.
принадлежащих промежутку.
По теореме Лагранжа имеем 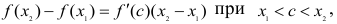 но по условиям теоремы f'(с)>0, следовательно
но по условиям теоремы f'(с)>0, следовательно 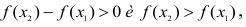 а это означает, что f(х) - возрастающая функция.
а это означает, что f(х) - возрастающая функция.
Отсюда следует, что знак производной функции свидетельствует о её возрастании или убывании на данном промежутке. Поэтому имеет смысл говорить об интервалах возрастания и убывания функций.
Третья часть теоремы очевидна - если f(х)- константа, то ее производная равна нулю: f'(х) = 0.
Пример №21
Определить области возрастания и убывания функции 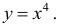
Решение:
Найдем производную данной функции и определим интервалы, в которых производная положительна и отрицательна.
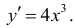
Очевидно, что производная положительна при х>0 и отрицательна при х<0. Следовательно, исследуемая функция является возрастающей на интервале 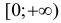 и убывающей на интервале
и убывающей на интервале 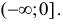
Экстремум функции
Особую роль в исследовании функций играют значения х, отделяющие интервал возрастания от интервала убывания или интервал убывания от интервала возрастания функции.
Определение. Точка 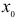 называется точкой максимума функции f'(х), если
называется точкой максимума функции f'(х), если 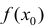 есть наибольшее значение функции f(х)в некоторой окрестности точки
есть наибольшее значение функции f(х)в некоторой окрестности точки 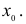 Определение. Точка
Определение. Точка 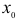 называется точкой минимума функции f(х), если
называется точкой минимума функции f(х), если
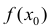 есть наименьшее значение функции f(х) в некоторой окрестности точки
есть наименьшее значение функции f(х) в некоторой окрестности точки 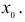
Точки максимума и минимума называются точками экстремума.
Теорема 1. (необходимое условие существование экстремума).
Если дифференцируемая функция у = f(x) имеет в точке 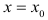 максимум или минимум, то её производная обращается в нуль в этой точке, т.е.
максимум или минимум, то её производная обращается в нуль в этой точке, т.е. 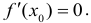
Обратное заключение неверно: не при всяком значении, при котором производная обращается в нуль, обязательно существует максимум и минимум.
Например, функция 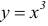 (рисунок 4.4) имеет в точке х = 0 производную равную нулю, но в этой точке функция не имеет ни максимума, ни минимума.
(рисунок 4.4) имеет в точке х = 0 производную равную нулю, но в этой точке функция не имеет ни максимума, ни минимума.
Если производная не существует в какой-либо точке (но существует в близлежащих точках), то в этой точке производная терпит разрыв.
Значения аргумента, при которых производная обращается в нуль f’(x) = 0 или терпит разрыв (f'(х) не существует), называют критическими точками. (Не всякая критическая точка является точкой экстремума).
Теорема 2. (достаточные условия существование экстремума).
Пусть функция y = f(x) непрерывна в некоторой точке 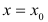 и производная функции в этой точке равна нулю. Тогда:
и производная функции в этой точке равна нулю. Тогда:
- если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то при
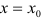 функция имеет максимум;
функция имеет максимум; - если при переходе слева направо через эту точку производная меняет знак с минуса на плюс, то при
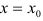 функция имеет минимум;
функция имеет минимум; - если при переходе слева направо через эту точку производная не меняет знака, значит в этой точке нет локального экстремума.
Точку 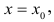 в которой производная функции обращается в нуль
в которой производная функции обращается в нуль 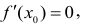 называют стационарной точкой. Точки, в которых
называют стационарной точкой. Точки, в которых 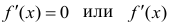 не существует, называют критическими точками. (Не всякая критическая точка является точкой экстремума).
не существует, называют критическими точками. (Не всякая критическая точка является точкой экстремума).
Пример №22
Исследовать на наличие локальных экстремумов функцию
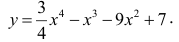
Решение:
Найдем производную функции 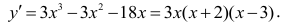
Очевидно, что 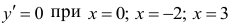 (критические точки).
(критические точки).
Проанализируем полученные точки в таблице 4.1.
Анализ функции 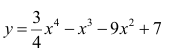 Таблица 4.1
Таблица 4.1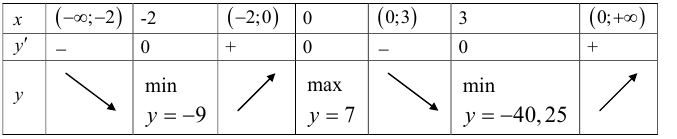
Итак, производная меняет знак при переходе слева направо через точки х = — 2 с минуса на плюс, значит в этих точках график функции имеет локальные минимумы. При переходе слева направо через точку х = 0 производная меняет знак с плюса на минус, значит в этой точке функция имеет локальный максимум.
Вычислим точки локальных экстремумов:
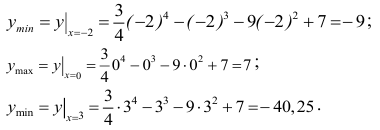
Выполним построение графика данной функции:
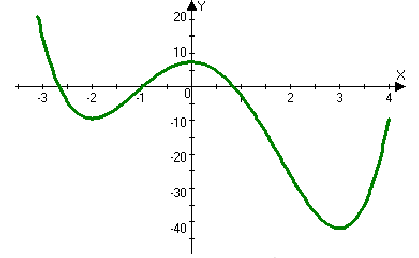
Рисунок 4.2 - График функции 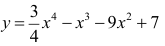
Ответ: минимумы в точках (-2;-9) и (3;-40,25) и максимум в точке (0;7).
Наибольшее и наименьшее значения непрерывной функции на замкнутом промежутке
Если функция f(х) непрерывна на отрезке 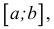 то она достигает на этом отрезке наименьшего и наибольшего значения.
то она достигает на этом отрезке наименьшего и наибольшего значения.
Наибольшее и наименьшее значение функции может быть достигнуто как в точках экстремума, так и на концах отрезка.
Для нахождения наибольшего и наименьшего значения функции на фиксированном отрезке изменения аргумента, необходимо:
- Найти производную функции
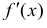
- Найти критические точки, в которых f'(x) = 0 или не существует.
- Найти значения функции на концах отрезка.
- Выбрать наибольшее и наименьшее из всех найденных значений.
Пример №23
Найти наибольшее и наименьшее значения функции
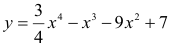 на интервале (-3;4,25), которая была ранее исследована на наличие экстремумов в примере 40.
на интервале (-3;4,25), которая была ранее исследована на наличие экстремумов в примере 40.
Решение:
Так как минимумы и максимумы на данном интервале уже найдены (см. пример 40), вычислим значения функции на концах интервала:
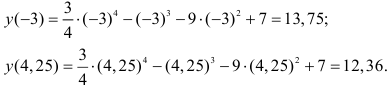
Для наглядности запишем полученные значения в таблицу 4.2.
Анализ наибольших и наименьших значений функции Таблица 4.2
Из таблицы видно, что данная функция на интервале (-3;4;25) имеет наибольшее значение у = 13,75 при х = -3 и наименьшее значение у = -40,25 при х = 3.
Замечание. Если требуется найти наибольшее и наименьшее значения функции на фиксированном отрезке изменения аргумента, то необходимо:
- Найти все максимумы и минимумы функции на отрезке.
- Найти значения функции на концах отрезка.
- Выбрать наибольшее и наименьшее из всех найденных значений.
Не следует путать, допустим, локальный максимум и максимальное значение функции на отрезке - последнее может быть на конце отрезка, где функция не имеет экстремума, а «принудительно» обрывается. Именно поэтому предусмотрен вышеприведенный пункт 2.
Выпуклость и вогнутость кривой
Мы говорим, что кривая обращена выпуклостью вверх на интервале 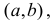 если все точки кривой лежат ниже любой её касательной на этом интервале.
если все точки кривой лежат ниже любой её касательной на этом интервале.
Мы говорим, что кривая обращена выпуклостью вниз на интервале 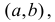 если все точки кривой лежат выше любой её касательной на этом интервале.
если все точки кривой лежат выше любой её касательной на этом интервале.
Кривую, обращенную выпуклостью вверх, будем называть выпуклой, а обращенную выпуклостью вниз - вогнутой.
Теорема 1. Если во всех точках интервала 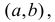 вторая производная функции f(х) отрицательна, то кривая на этом интервале выпукла.
вторая производная функции f(х) отрицательна, то кривая на этом интервале выпукла.
Теорема 2. Если во всех точках интервала 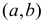 вторая производная функции f(х) положительна, то кривая на этом интервале вогнута.
вторая производная функции f(х) положительна, то кривая на этом интервале вогнута.
Точки перегиба
Определение. Точка, отделяющая выпуклую часть непрерывной кривой от вогнутой части, называется точкой перегиба.
Теорема (достаточные условия того, что данная точка кривой является точкой перегиба). Пусть кривая определяется уравнением у= f(х). Если 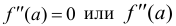 не существует и при переходе через значение х = а вторая производная меняет знак, то точка кривой с абсциссой х = а есть точка перегиба.
не существует и при переходе через значение х = а вторая производная меняет знак, то точка кривой с абсциссой х = а есть точка перегиба.
Примем данную теорему без доказательства.
Пример №24
Определить точки перегиба и интервалы выпуклости и вогнутости функции
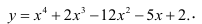
Решение:
Найдем вторую производную функции и её корни
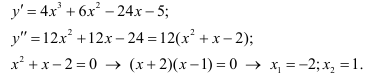
Проверив изменение знака второй производной при переходе через критические точки 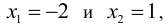 выясняем, что данные точки являются точками перегиба, причем при
выясняем, что данные точки являются точками перегиба, причем при 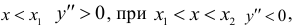 при
при 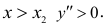 Вычислим значения функции в точках перегиба, получаем точки на графике (-2;-36) и (1; -12).
Вычислим значения функции в точках перегиба, получаем точки на графике (-2;-36) и (1; -12).
Ответ: Точки перегиба (-2;-36) и (1;-12).Кривая вогнута на интервалах 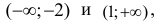 выпукла на интервале (-2;1). На рисунке 4.3 хорошо видны интервалы выпуклости и вогнутости функции
выпукла на интервале (-2;1). На рисунке 4.3 хорошо видны интервалы выпуклости и вогнутости функции 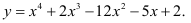
Рисунок 4.3 - Точки перегиба функции 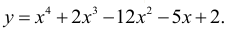
Асимптоты
Определение. Прямая линия называется асимптотой кривой у = f(x), если расстояние от точки М, лежащей на этой кривой, до прямой стремится к нулю при удалении точки М в бесконечность.
Различают три вида асимптот: горизонтальные, вертикальные и наклонные.
Горизонтальные асимптоты. Если существует предел 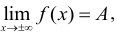 то прямая у = А является горизонтальной асимптотой кривой у = f(x).
то прямая у = А является горизонтальной асимптотой кривой у = f(x).
Вертикальные асимптоты. Если существует хотя бы один из пределов
 то прямая х = А является вертикальной асимптотой кривой у = f(x).
то прямая х = А является вертикальной асимптотой кривой у = f(x).
Наклонные асимптоты. Если существуют пределы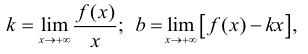
или
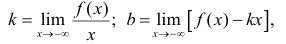
то прямая у = kх + b является наклонной асимптотой кривой 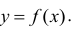 Заметим, что горизонтальную асимптоту можно рассматривать как частный случай наклонной асимптоты при k=0.
Заметим, что горизонтальную асимптоту можно рассматривать как частный случай наклонной асимптоты при k=0.
Пример №25
Найти асимптоты кривой 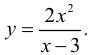
Решение:
1. Горизонтальные асимптоты: 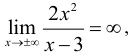 значит горизонтальных
значит горизонтальных
асимптот нет.
2. Вертикальные асимптоты: кривая имеет вертикальную асимптоту х = 3, так как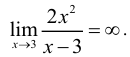
3. Наклонные асимптоты:
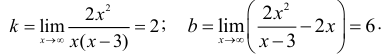
Следовательно, кривая имеет наклонную асимптоту у = 2х + 6.
На рисунке 4.4 изображены вертикальная х = 3 и наклонная у = 2х + 6 асимптоты функции 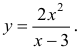
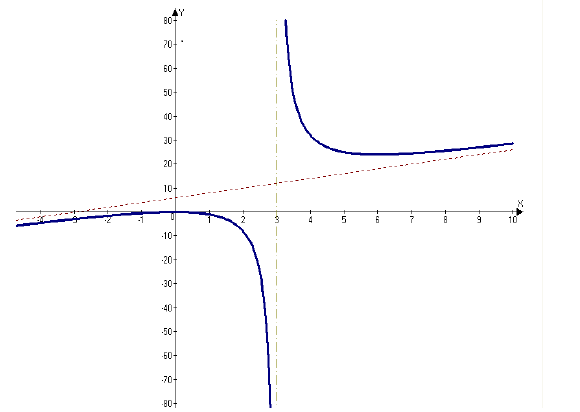
Рисунок 4.4 - Асимптоты графика функции 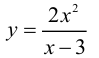
Общий план исследования функций и построения графиков
- определение области существования функции;
- нахождение точек пересечения графика функции с осями координат (если это не вызывает затруднений);
- выяснение вопроса о четности и нечетности функции;
- определение точек разрыва функции;
- нахождение асимптот графика функции;
- нахождение точек экстремумов;
- нахождение интервалов возрастания и убывания функции;
- нахождение точек перегиба;
- определение областей выпуклости и вогнутости;
- построение графика.
Замечание 1. Если функция исследуется на определенном интервале, то при необходимости следует найти максимальные и минимальные значения функции.
Замечание 2. Если исследуемая функция четная, то достаточно построить её график при положительных значениях аргумента. График четной функции симметричен относительно оси ординат (ось симметрии). Если исследуемая функция нечетная, то достаточно построить её график при положительных значениях аргумента. График нечетной функции симметричен начала координат (центр симметрии).
Замечание 3. Все области экономической теории и практики в определенной, иногда значительной, мере используют графическое представление функциональных зависимостей.
Пример №26
Исследовать функцию 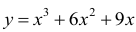 и построить ее график.
и построить ее график.
Решение:
1. Область определения функции - все множество действительных чисел; 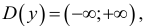 т.е. нет точек разрыва функции, нет вертикальных асимптот.
т.е. нет точек разрыва функции, нет вертикальных асимптот.
2. Функция общего вида, т.е. ни четная, ни нечетная: 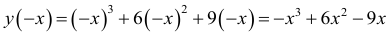
3. Функция непериодическая.
4. Пересечение с осями координат.
OY: 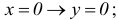 Точка (0,0)- начало координат.
Точка (0,0)- начало координат.
ОХ: 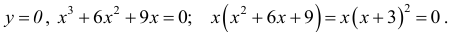
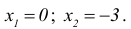 Точки пересечения с осью ОХ: (0,0) и (-3,0).
Точки пересечения с осью ОХ: (0,0) и (-3,0).
5. Асимптоты. Вертикальных асимптот нет. Исследуем наклонные асимптоты:
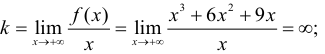 т.к. предел не существует, следовательно нет наклонных асимптот.
т.к. предел не существует, следовательно нет наклонных асимптот.
6. Точки экстремума:
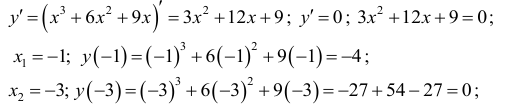
Получены точки экстремума: (-1;-4) и (-3;0).
7. Сведем все полученные данные в таблицу 4.3 и заполним ее.
Таблица 4.3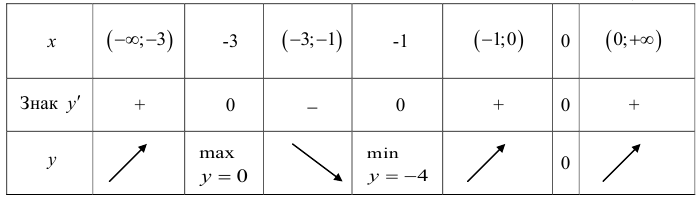
На участках: 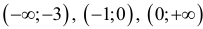 функция возрастает.
функция возрастает.
На участке (-3;-1) функция убывает.
8. Точки перегиба, 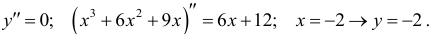 Точка перегиба (-2;-2). График выпуклый на участке:
Точка перегиба (-2;-2). График выпуклый на участке: 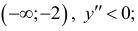 вогнут-на участке:
вогнут-на участке: 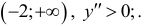
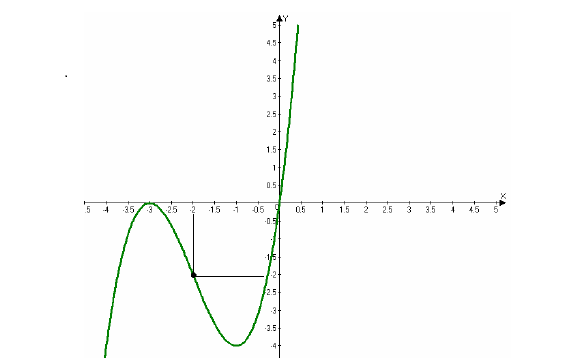
Рисунок 4.3 - График функции 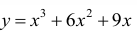
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |