Преобразования декартовой системы координат с примерами решения

Содержание:

Преобразования декартовой системы координат

Параллельный перенос и поворот системы координат

1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):

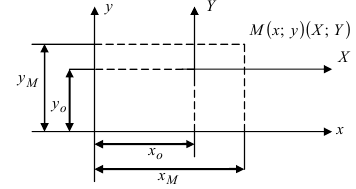
Рис. 46. Параллельный перенос одной системы координат относительно другой системы.

Систему координат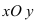

Пример:

Дана точка М(3;2) и начало новой системы координат 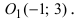Вычислить положение точки М в новой системе отсчета.

Решение:

Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим 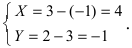Следовательно, точка М в новой системе отсчета имеет координаты М(4; -1).

2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол 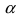(Рис. 47):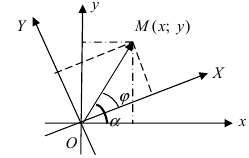

Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.

Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны 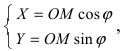а координаты этой точки в старой системе координат равны 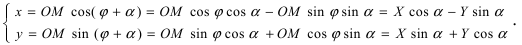Таким образом формулы перехода от новых координат произвольной точки М к старым имеет вид 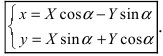В матричном виде эти равенства можно записать в виде 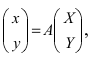где матрица перехода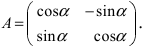

Найдем обратное преобразование системы координат, найдем матрицу 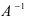обратную к матрице А: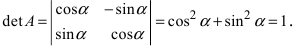

Найдем алгебраические дополнения всех элементов

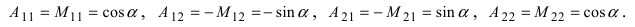Запишем обратную матрицу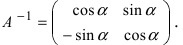

Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.

Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.

Таким образом, имеем 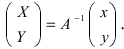Следовательно, формулы перехода от старой системы отсчета к новой системе отсчета имеют вид:

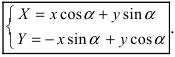
Пример:

Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол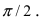

Решение:

Воспользуемся полученными формулами 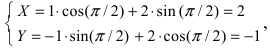т.е. в новой системе координат точка имеет координаты М(2; -1).

Рассмотрим применение преобразования координат:

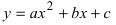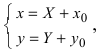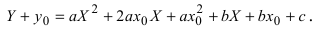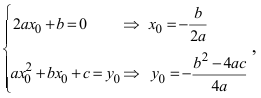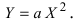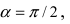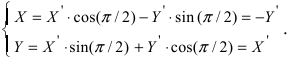а) Преобразовать уравнение параболы к каноническому виду. Проведем параллельный перенос системы координат получим Выберем начало отсчета новой системы координат так, чтобы выполнялись равенства тогда уравнение принимает вид Выполним поворот системы координат на угол тогда Подставим найденные соотношения в уравнение параболы 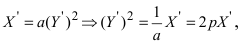где параметр параболы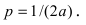

Пример:

Преобразовать уравнение параболы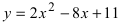 к каноническому виду.

Решение:

Найдем начало отсчета новой системы координат после параллельного переноса 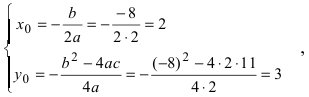т.е. точка 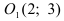- начало координат новой системы отсчета. В этой системе уравнение параболы имеет вид 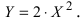Проведем поворот системы отсчета на угол 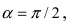тогда

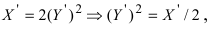следовательно, параметр параболы р = 1/4.

б) Выяснить, какую кривую описывает функция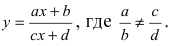

Проведем следующее преобразование 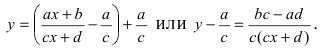Производя параллельный перенос системы координат, вводя обозначение

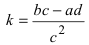и новые координаты 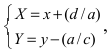получим уравнение 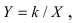которое описывает равнобочную гиперболу.

• Заказать решение задач по высшей математике

Полярные координаты. Замечательные кривые

Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом 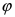между радиус-вектором и полярной осью (угол отсчитывается против часовой стрелки).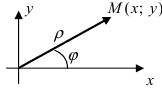

Рис. 48. Полярная система координат.

Главными значениями угла 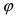являются значения, лежащие в интервале 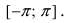Из рисунка видно, что декартовы и полярные координаты связаны формулами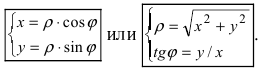

Рассмотрим замечательные кривые в полярной системе координат:

1. Спираль Архимеда 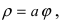где число 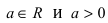(Рис. 49). Для построения кривой в полярной системе координат, разобьем декартову плоскость лучами с шагом по углу 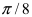и на каждом луче отложим ему соответствующее значение р.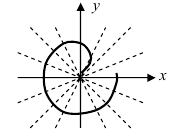

Рис. 49. Спираль (улитка) Архимеда.

2. Уравнение окружности: уравнение 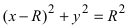описывает окружность с центром в точке A(R; 0) и радиусом R (Рис. 50). В полярной системе координат уравнение принимает вид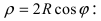

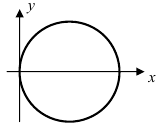
Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.

3. Уравнение 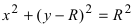описывает окружность с центром в т. А(0; R) и радиусом R (Рис. 51). В полярной системе координат уравнение принимает вид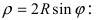

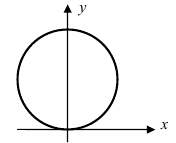
Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.

4. Кардиоиды: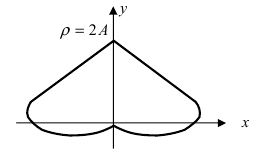

Рис. 52. Кардиоида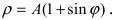

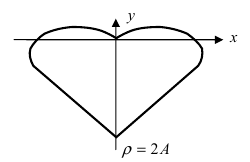
Рис. 53. Кардиоида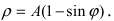

Аналогично выглядят кардиоиды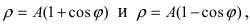 но они вытянуты вдоль оси абсцисс Ох.

5. Петля: 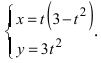Величина 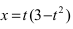равна нулю при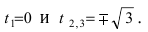

Для первого корня у = 0, а для второго и третьего - у = 9 . Следовательно, петля имеет вид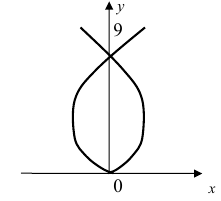

Рис. 54. Петля.