Преобразование треугольника сопротивлений в эквивалентную звезду

Преобразование треугольника сопротивлений в эквивалентную звезду и обратное преобразование:

При расчете разветвленных цепей и, особенно, при определении их входных сопротивлений может возникнуть вопрос о преобразовании треугольника сопротивлений в эквивалентную звезду или обратного преобразования. Такая процедура становится возможной при условии неизменности потенциалов на зажимах преобразуемого участка цепи.

Рассмотрим участок цепи, соединенный «треугольником» (рис. 3.7.a) и покажем его преобразование в эквивалентную «звезду» (рис. 3.7.b).

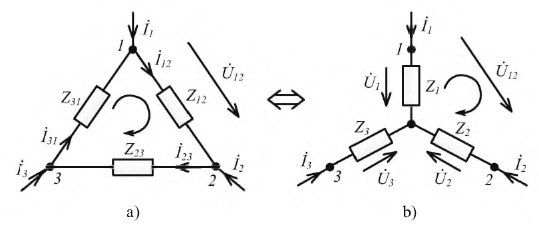
Рис. 3.7. Взаимное преобразование «треугольника» сопротивлений в «звезду»

Составим уравнения по первому и второму законам Кирхгофа для «треугольника».

По первому закону Кирхгофа:

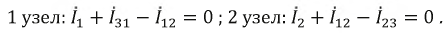
По второму закону Кирхгофа:

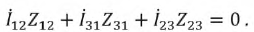
Решим эту систему уравнений, например, относительно тока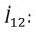

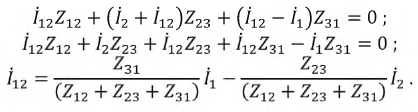
Определим напряжение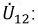

в схеме «треугольник»:

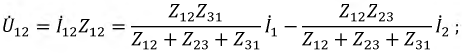
в схеме «звезда»:

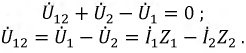
При этом должно выполняться равенство: 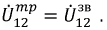Приравнивая эти выражения, получим формулы перехода от соединения сопротивлений «треугольником» к сопротивлениям «звезды»

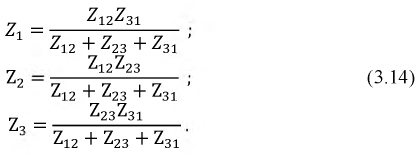
Покажем на примере (рис. 3.8) применимость данного преобразования.

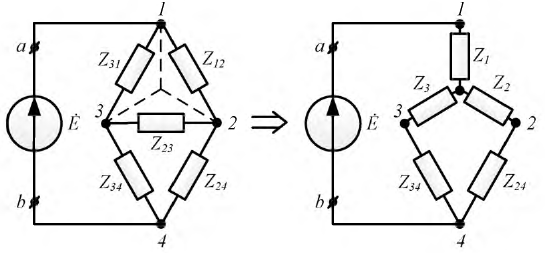
Рис. 3.8. Преобразование «треугольника» сопротивлений в «звезду»

Обратное преобразование из «звезды» в «треугольник» (рис. 3.9) выполняется по формулам перехода:

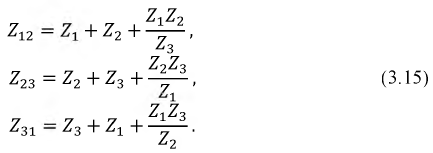
В результате преобразований соответствующих схем и расчета сопротивлений по формулам (3.14) или (3.15) упрощенные схемы (см. рис. 3.8 и 3.9) состоят из последовательно-параллельно соединенных сопротивлений и расчет эквивалентного сопротивления значительно упрощается.

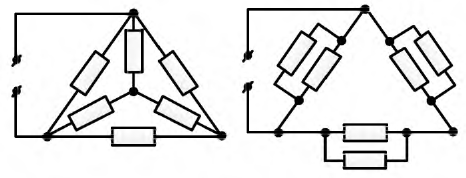
Рис. 3.9. Преобразование «звезды» сопротивлений в «треугольник»