
Преобразование фигур в геометрии с примерами решения
Содержание:
Отображение плоскости на себя, которое сохраняет расстояния между точками, называется движением. Примерами движения являются такие преобразования, как центральная симметрия, осевая симметрия, поворот (вращение), скольжение.
Поворот:
Пусть, заданы точка О и угол 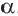
1. Если точка А не совпадает с точкой О, то 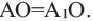
2. Если точка А совпадает с точкой О, то точки 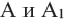 совпадают.
совпадают.
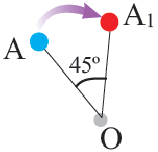
Пример 1. Угол поворота 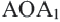 равен 45°. Точка А совершила поворот вокруг точки О, на угол 45° по часовой стрелке.
равен 45°. Точка А совершила поворот вокруг точки О, на угол 45° по часовой стрелке.
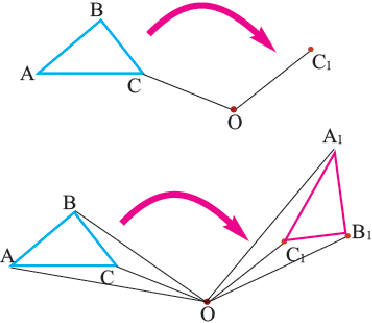
Пример 2. Проанализируйте последовательность шагов, при котором совершается поворот треугольника 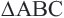 вокруг точки О, на угол 120°. Повторите эти шаги, выполнив построение в тетради.
вокруг точки О, на угол 120°. Повторите эти шаги, выполнив построение в тетради.
- 1. Соедините точку О и точку С отрезком прямой.
- 2. При помощи транспортира от ОС постройте угол 120° в направлении по часовой стрелке и циркулем отложите отрезок
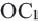 , конгруэнтный отрезку ОС.
, конгруэнтный отрезку ОС. - 3. Потому же правилу соедините точку О с точками А и В. Постройте отрезки
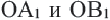 конгруэнтные полученным отрезкам OA и ОВ и составляющие с ними угол 120°. Точки
конгруэнтные полученным отрезкам OA и ОВ и составляющие с ними угол 120°. Точки  являются вершинами нового треугольника. Соедините эти точки.
являются вершинами нового треугольника. Соедините эти точки.
Примечание. Центральная симметрия является поворотом плоскости относительно центра симметрии на 180°.
Исследуйте и начертите в тетради:
На рисунке показана последовательность шагов, которые выполняются при повороте треугольника  с вершинами А( 4;1), В( 3;5),С( 1;3) на угол 90° в направлении по часовой стрелке.
с вершинами А( 4;1), В( 3;5),С( 1;3) на угол 90° в направлении по часовой стрелке.

При повороте на угол 90" в направлении по часовой стрелке координаты вершин изменяются следующим образом.

Отношения, пропорция
Свойства пропорции
Если 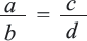 то,
то, 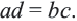
Если 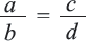 то,
то, 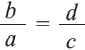
Если 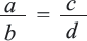 то,
то, 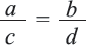
Если 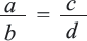 то,
то, 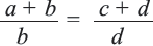
Пропорциональные отрезки
Практическая работа. Пропорциональные отрезки.
1. Начертите в тетради 3 параллельные прямые.

2. Проведите 3 секущие, которые пересекают эти прямые.
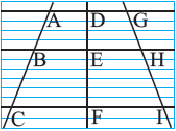
3. Измерьте отрезки АВ, ВС, AC, DE, EF, DF, GH, HI и GI.
4. Запишите и вычислите следующие отношения
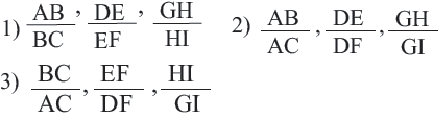
5. Можно ли по результатам сказать, что параллельные линии делят секущие на пропорциональные отрезки? Пропорциональные отрезки
Если для отрезков АВ, CD, 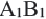 , C1D1 выполняется
, C1D1 выполняется 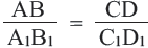 , то отрезки АВ и CD пропорциональны отрезкам
, то отрезки АВ и CD пропорциональны отрезкам 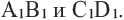
Теорема. Параллельные линии, пересекающие стороны угла, отсекают от них пропорциональные отрезки.
Доказательство. Допустим, что параллельные прямые пересекают стороны угла А в точках В и С, 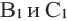 . Для простоты, предположим, что существует отрезок длины
. Для простоты, предположим, что существует отрезок длины 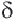 такой, что он помещается целое число раз как в отрезке АС, так и в отрезке
такой, что он помещается целое число раз как в отрезке АС, так и в отрезке 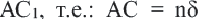 ,
, 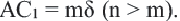 Разделим отрезок АС на равные отрезки длиной
Разделим отрезок АС на равные отрезки длиной 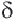 в количестве
в количестве 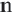 раз. В этом случае, одной из точек деления будет точка
раз. В этом случае, одной из точек деления будет точка 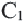 . Через точки деления проведём прямые, параллельные ВС. По теореме Фалеса эти прямые разобьют отрезок АВ на равные отрезки некоторой длины
. Через точки деления проведём прямые, параллельные ВС. По теореме Фалеса эти прямые разобьют отрезок АВ на равные отрезки некоторой длины 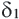 . Получим, что
. Получим, что 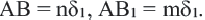 Отсюда
Отсюда 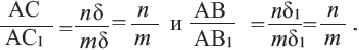 Таким образом,
Таким образом, 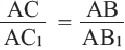
Подобные четырехугольники, подобные треугольники
Подобными называются фигуры одинаковые по форме и у которых соответствующие размеры пропорциональны. Например, все квадраты подобны друг другу, так же как и окружности разных радиусов.

Подобными называются многоугольники, у которых соответствующие углы конгруэнтны, а соответствующие стороны являются пропорциональными отрезками. Например, на рисунке четырёхугольники ABCD и EFGH являются подобными четырёхугольниками. Так как, 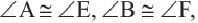
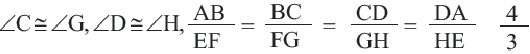
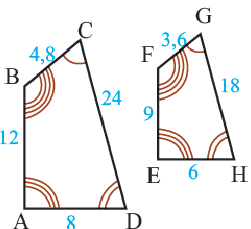
У подобных треугольников соответствующие углы конгруэнтны, а соответствующие стороны являются пропорциональными отрезками. Здесь, говоря о соответствующих сторонах, имеются в виду стороны, которые находятся напротив конгруэнтных углов. На рисунке для 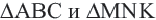 имеем:
имеем:

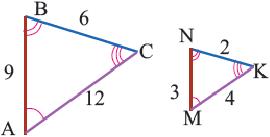
Так как 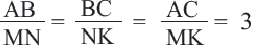 , то
, то 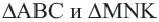 являются подобными треугольниками. Подобие обозначается знаком
являются подобными треугольниками. Подобие обозначается знаком 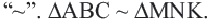 Отношение соответствующих сторон называется коэффициентом подобия и обозначается буквой
Отношение соответствующих сторон называется коэффициентом подобия и обозначается буквой 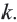 Коэффициент подобия треугольников на рисунке равен 3.
Коэффициент подобия треугольников на рисунке равен 3.
Периметр подобных многоугольников
Теорема. Отношение периметров двух подобных многоугольников равно отношению соответствующих сторон (или коэффициенту подобия)
Если  , то
, то 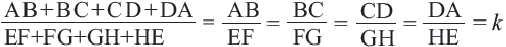
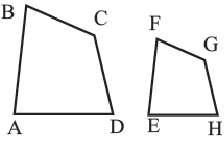
Запишите доказательство теоремы, приняв коэффициент подобия за 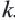 . Для этого можно использовать равенство
. Для этого можно использовать равенство 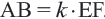 , которое следует, из отношения соответствующих сторон.
, которое следует, из отношения соответствующих сторон.
Признаки подобия треугольников
Признак подобия УУ (угол угол)
Если два угла одного треугольника конгруэнтны двум углам другого треугольника, то такие треугольники подобны. Этот признак подобия коротко записывается как УУ.

Признак подобия ССС
Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны. Этот признак подобия коротко записывается как ССС.

Признак подобия СУС
Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами конгруэнтны, то такие треугольники подобны. Этот признак подобия коротко записывается как СУС.

Подобие прямоугольных треугольников
Высота, проведенная к гипотенузе
Теорема. Высота, проведённая из вершины прямого угла прямоугольного треугольника, делит его на два подобных треугольника, каждый из которых подобен данному треугольнику.
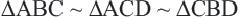
Доказательство данной теоремы проводится на основании признака подобия УУ Для каждого из трёх треугольников нужно определить два конгруэнтных угла.
Среднее геометрическое
Среднее геометрическое. Для положительных чисел а и b средним геометрическим называется положительное число 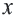 , удовлетворяющее равенству
, удовлетворяющее равенству 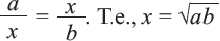
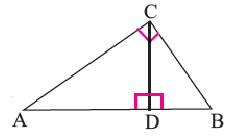
Высота, проведённая из вершины прямого угла на гипотенузу, делит её на два отрезка (на рисунке AD и DB) Здесь отрезки AD и DB являются проекциями катетов АС и ВС на гипотенузу, соответственно.
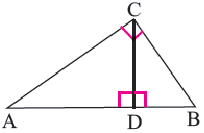
Следствие 1. Высота прямоугольного треугольника, опущенная из вершины прямого угла есть среднее геометрическое отрезков, на которые она делит гипотенузу.
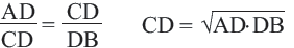
Следствие 2. Каждый катет прямоугольного треугольника есть среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу.
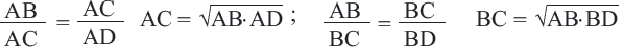
Применение подобия треугольников
Пропорциональные отрезки
Теорема. Прямая, пересекающая две стороны треугольника, и параллельная третьей стороне делит стороны на пропорциональные отрезки.
Если 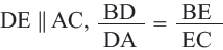
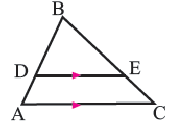
Обратная теорема. Если прямая, пересекающая две стороны треугольника делит их на пропорциональные отрезки, то эта прямая параллельна третьей стороне.
Если 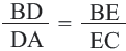 , то
, то 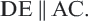
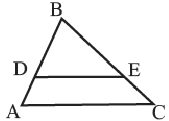
Высоты, медианы и биссектрисы подобных треугольников
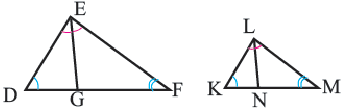
Теорема 1. Если два треугольника подобны, то отношение длин соответствующих высот равны отношению длин соответствующих сторон.
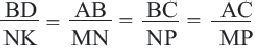
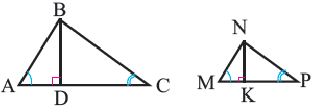
Теорема 2. Если два треугольника подобны, то отношение длин соответствующих медиан равны отношению длин д соответствующих сторон.
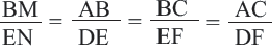
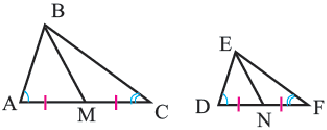
Теорема 3. Если два треугольника подобны, то отношение длин соответствующих биссектрис равны отношению длин соответствующих сторон.
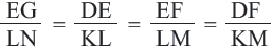
Свойство биссектрисы треугольника
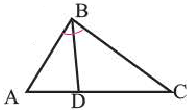
Теорема. Биссектриса треугольника делит противоположную сторону на отрезки пропорциональные двум другим сторонам.
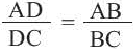
Теорема. Свойство медиан треугольника
Медианы треугольника пересекаются в одной точке и делятся в точке пересечения в отношении 2:1, начиная от вершины.
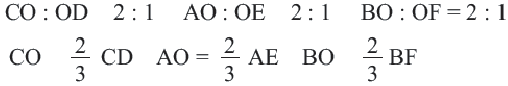
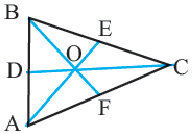
Точка пересечения медиан называется центром тяжести треугольника.
Доказательство теоремы представлено в виде двухстолбчатой таблицы.
Дано: 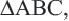 CD и AE медианы треугольника
CD и AE медианы треугольника
Доказать: AO:OE=CO:OD=BO:OF=2:1
Доказательство: соединим точки O и E.
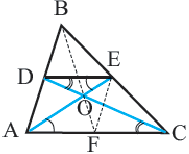

Преобразование подобия, гомотетия
Гомотетия
Преобразование плоскости на себя, при котором расстояние между любыми двумя точками изменяется в одно и то же число раз называется преобразованием подобия. Фигуры называются подобными, если одна фигура переводится в другую преобразованием подобия. Если при преобразовании подобия точки А и В на плоскости соответственно преобразованы в точки 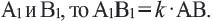 Число
Число 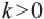 называется коэффициентом подобия. Преобразование подобия при
называется коэффициентом подобия. Преобразование подобия при 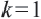 называется движением. Предположим, что заданы точка О и число
называется движением. Предположим, что заданы точка О и число 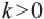 . Преобразование плоскости на себя при котором для произвольной точки А плоскости и преобразованной точки
. Преобразование плоскости на себя при котором для произвольной точки А плоскости и преобразованной точки 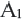 выполняется равенство
выполняется равенство 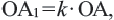 называется гомотетией. Точка О называется центром гомотетии, число
называется гомотетией. Точка О называется центром гомотетии, число 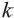 - коэффициентом гомотетии, точки А и
- коэффициентом гомотетии, точки А и 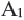 гомотетичными точками.
гомотетичными точками.
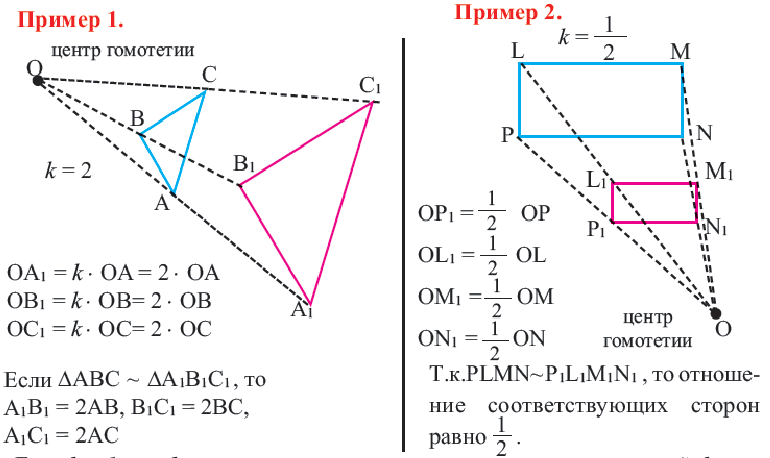
Если 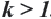 , то фигура увеличивается относительно изначальной фигуры.
, то фигура увеличивается относительно изначальной фигуры.
Если 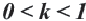 , то фигура уменьшается относительно изначальной фигуры.
, то фигура уменьшается относительно изначальной фигуры.
Если 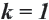 , то фигура конгруэнтна изначальной фигуре.
, то фигура конгруэнтна изначальной фигуре.
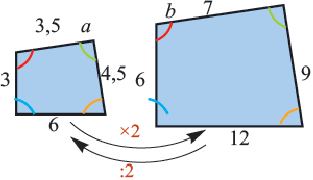
Площади подобных фигур
Теорема. Отношение площадей подобных фигур равно квадрату коэффициента подобия. Например, если отношение соответствующих сторон двух подобных четырёхугольников равно 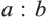 , то отношение площадей равно
, то отношение площадей равно 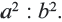
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |