
Преобразование чертежа в начертательной геометрии с примерами
Содержание:
Преобразование чертежа:
Изложенный в предыдущих разделах материал позволяет сделать вывод, что решение задач позиционного и, главным образом, метрического характера значительно облегчается, если г.о. (прямые или плоскости) занимают частные положения относительно плоскостей проекций. Перевода г.о. из общего в частное положение можно достичь использованием способов преобразования чертежа. При ортогональном проецировании такой перевод может осуществляться двумя путями:
- - изменением положения плоскостей проекций относительно г.о., который остается неподвижным;
- - перемещением г.о. относительно плоскостей проекций, при этом последние остаются неподвижными.
Первый путь составляет теоретическую базу способа перемены плоскостей проекций, второй лежит в основе способов плоскопараллельного перемещения и вращения.
Способ перемены плоскостей проекции
Сущность способа перемены (замены) плоскостей проекций заключается в том, что одну из плоскостей проекций ортогональной системы 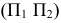
Рассмотрим механизм введения дополнительной плоскости проекций (рис.110). Плоскость  заменяем на новую плоскость
заменяем на новую плоскость  расположенную к
расположенную к 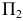 под углом, не равным 90° (в данном случае этот угол выбран произвольно). При этом
под углом, не равным 90° (в данном случае этот угол выбран произвольно). При этом 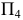 будет перпендикулярна горизонтальной плоскости проекций
будет перпендикулярна горизонтальной плоскости проекций 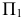 и пересекать ее по оси
и пересекать ее по оси 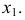 Точка ортогонально проецируется на
Точка ортогонально проецируется на 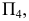 образуя новую проекцию
образуя новую проекцию 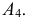 Таким образом, будем иметь две системы плоскостей проекций - старую
Таким образом, будем иметь две системы плоскостей проекций - старую 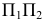 и новую
и новую 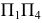 с общей плоскостью
с общей плоскостью 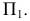 Из рис. 110 видно, что расположение т.
Из рис. 110 видно, что расположение т. 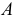 относительно общей плоскости проекций не изменяется, т.е. координата
относительно общей плоскости проекций не изменяется, т.е. координата 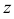 точки
точки 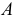 остается постоянной в обеих системах.
остается постоянной в обеих системах.
Эти же рассуждения сохраняются и при построении новой проекции точки на эпюре, полученном после совмещения плоскостей  и
и  с плоскостью
с плоскостью  (рис. 111).
(рис. 111).
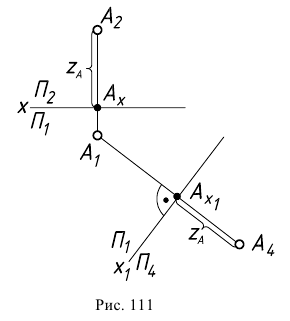
В нашем примере равенство аппликат у новой  и старой
и старой 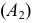 проекций точки
проекций точки 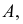 а также использование в обеих системах прямоугольного проецирования делают построение новой проекции на эпюре чрезвычайно простым. Оно состоит в том (см. рис. 111), что через старую горизонтальную проекцию точки
а также использование в обеих системах прямоугольного проецирования делают построение новой проекции на эпюре чрезвычайно простым. Оно состоит в том (см. рис. 111), что через старую горизонтальную проекцию точки 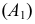 проводят линию проекционной связи, перпендикулярную новой оси
проводят линию проекционной связи, перпендикулярную новой оси 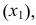 и откладывают на ней, от точки пересечения с осью, отрезок
и откладывают на ней, от точки пересечения с осью, отрезок 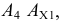 равный исходной координате
равный исходной координате 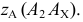
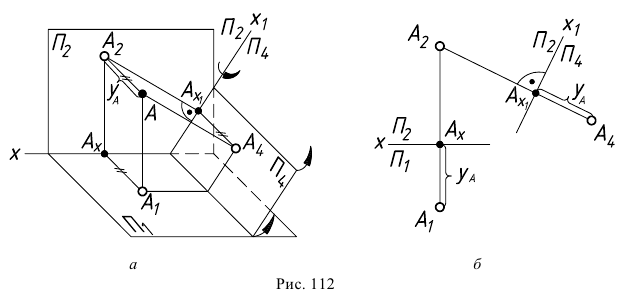
При замене горизонтальной плоскости проекций на новую (рис.112, а) для двух систем остается постоянной плоскость 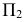 и, следовательно, координата
и, следовательно, координата 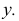 Это постоянство координаты
Это постоянство координаты  лежит в основе построения эпюра (рис. 112, б).
лежит в основе построения эпюра (рис. 112, б).
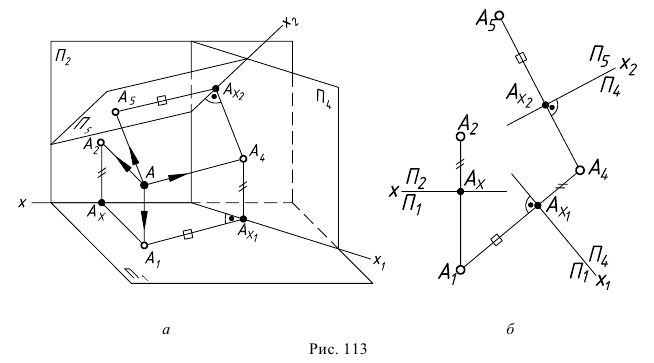
При решении задач приходится менять либо одну из заданных плоскостей проекций, либо последовательно обе, если заменой одной плоскости не удается получить необходимого расположения проецируемого г.о. по отношению к новой плоскости проекций. Механизм такой двойной замены плоскостей проекций показан на примере построения проекций точки (рис. 113, а).
Сначала плоскость проекций  заменяют плоскостью проекций
заменяют плоскостью проекций  а затем в место плоскости проекций
а затем в место плоскости проекций 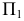 вводят плоскость
вводят плоскость 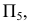 т.е. последовательно переходят от системы плоскостей проекций
т.е. последовательно переходят от системы плоскостей проекций 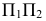 к системе
к системе 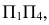 а затем от системы плоскостей
а затем от системы плоскостей 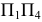 к системе
к системе 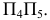
На эпюре (рис. 113, б) для построения новых проекций 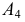 и
и 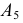 используют неизменность отрезка
используют неизменность отрезка 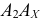 при переходе от системы
при переходе от системы 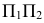 к системе
к системе 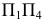 и отрезка
и отрезка 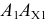 при переходе от системы
при переходе от системы  к системе
к системе 
Следует отметить, что при введении новой плоскости проекций (а следовательно, и новой оси на эпюре) удаление последней от заданного г.о. (проекции г.о.) выбирается произвольно, так как не влияет на конечный результат построений. Важную роль играет лишь расположение новой плоскости (оси) относительно г.о. (проекции г.о.).
Преобразование прямой общего положения в линию уровня и в проецирующую прямую
Первое преобразование (замена). Переведем прямую общего положения  в положение уровня. Для этого заменим одну из плоскостей проекций системы
в положение уровня. Для этого заменим одну из плоскостей проекций системы 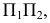 например
например 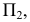 на новую плоскость
на новую плоскость 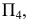 которая будет параллельна
которая будет параллельна 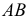 и перпендикулярна старой плоскости
и перпендикулярна старой плоскости 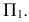 На
На 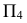 прямая проецируется, в этом случае, в натуральную величину (положение уровня).
прямая проецируется, в этом случае, в натуральную величину (положение уровня).
Необходимые построения на эпюре, выполняемые при первой замене плоскости проекций следующие (рис. 114):
- проводится ось
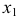 параллельно горизонтальной проекции прямой
параллельно горизонтальной проекции прямой 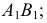
- проводятся линии проекционной связи из
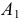 и
и 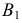 перпендикулярно оси
перпендикулярно оси 
- для построения проекции
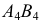 на линиях связи от новой оси
на линиях связи от новой оси 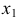 откладываются расстояния, равные аппликатам точек
откладываются расстояния, равные аппликатам точек  и
и 
Проекция  - натуральная величина прямой
- натуральная величина прямой 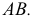
Угол 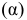 между
между 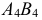 и осью
и осью 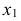 - угол наклона прямой к плоскости проекций
- угол наклона прямой к плоскости проекций 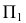 (вариант решения задачи на определение угла наклона прямой общего положения к
(вариант решения задачи на определение угла наклона прямой общего положения к 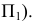
Второе преобразование (замена). Еще одну замену плоскости проекции выполним для перевода прямой 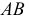 в проецирующее положение. При этом за «старую» систему плоскостей проекций принимаем уже не
в проецирующее положение. При этом за «старую» систему плоскостей проекций принимаем уже не 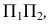 а
а 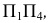 в которой прямая
в которой прямая 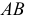 является линией уровня.
является линией уровня.
Заменим старую плоскость проекций 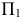 на новую плоскость проекций
на новую плоскость проекций 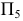 так, чтобы
так, чтобы 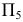 была перпендикулярна прямой
была перпендикулярна прямой 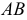 и плоскости проекций
и плоскости проекций 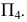 На эпюре (рис. 115) выполняются следующие построения:
На эпюре (рис. 115) выполняются следующие построения:
- проводится ось
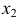 перпендикулярно
перпендикулярно 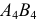 и линия проекционной связи как продолжение
и линия проекционной связи как продолжение 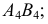
- на ней от оси
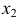 откладывается расстояние, равное величине удаления проекций
откладывается расстояние, равное величине удаления проекций 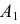 и
и 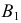 от оси
от оси 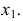 На чертеже эти отрезки обозначены
На чертеже эти отрезки обозначены 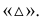
В результате получаем проекцию - точку  прямой, которая заняла проецирующее положение относительно плоскости проекций
прямой, которая заняла проецирующее положение относительно плоскости проекций 
Преобразование плоскости общего положения в проецирующую плоскость и в плоскость уровня
Первое преобразование (замена). При выполнении этого этапа дополнительную плоскость проекций следует ввести перпендикулярно одной из линий уровня плоскости - горизонтали или фронтали. Именно в этом случае заданная плоскость займет проецирующее положение относительно новой плоскости проекций.
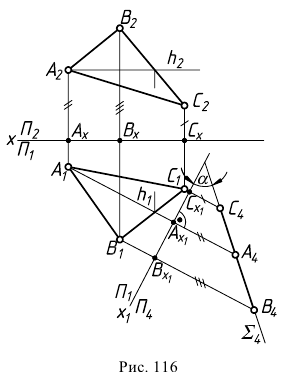
В случае замены фронтальной плоскости проекций выполняются следующие построения (рис. 116):
- строятся проекции
 горизонтали
горизонтали  плоскости
плоскости 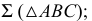
- проводится ось проекций
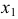 перпендикулярно
перпендикулярно 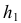 - горизонтальной проекции горизонтали;
- горизонтальной проекции горизонтали; - проводятся линии проекционной связи из точек
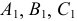 перпендикулярно
перпендикулярно - на линиях связи от оси
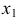 откладываются соответствующие отрезки и строится проекция
откладываются соответствующие отрезки и строится проекция 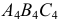 плоскости
плоскости 
 которая вырождается на
которая вырождается на 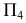 в прямую линию
в прямую линию 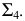 На новой плоскости проекций
На новой плоскости проекций 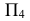 угол
угол 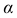 наклона плоскости
наклона плоскости 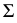 к
к 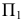 изобразится в натуральную величину.
изобразится в натуральную величину.
Второе преобразование (замена) позволяет перевести плоскость
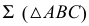 из проецирующего положения в положение плоскости уровня. Для этого дополнительную плоскость проекций
из проецирующего положения в положение плоскости уровня. Для этого дополнительную плоскость проекций 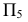 вводят параллельно заданной плоскости, образуя при этом с плоскостью
вводят параллельно заданной плоскости, образуя при этом с плоскостью  ещё одну ортогональную систему плоскостей проекций
ещё одну ортогональную систему плоскостей проекций  В этой новой системе заданная плоскость станет плоскостью уровня и спроецируется на
В этой новой системе заданная плоскость станет плоскостью уровня и спроецируется на  в натуральную величину.
в натуральную величину.
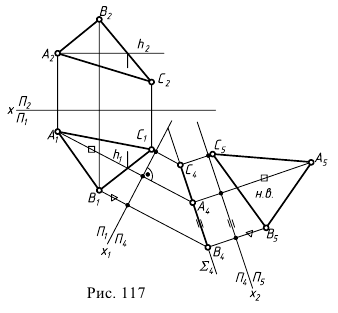
На эпюре (рис. 117) строятся:
- ось проекций
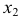 параллельно следу
параллельно следу 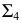 данной плоскости на
данной плоскости на 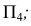
- линии проекционной связи из
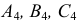 перпендикулярно
перпендикулярно 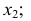
- с использованием соответствующих отрезков строится проекция
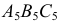 плоскости в виде натуральной плоской фигуры (вариант решения задачи на нахождение н.в. плоской фигуры, занимающей проецирующее положение).
плоскости в виде натуральной плоской фигуры (вариант решения задачи на нахождение н.в. плоской фигуры, занимающей проецирующее положение).
Следует помнить: преобразовать прямую общего положения в проецирующую прямую (или плоскость общего положения в плоскость уровня) выполняя только одну замену плоскости проекций невозможно. Это следует из того, что новая дополнительная плоскость проекций, перпендикулярная прямой общего положения (или параллельной плоскости общего положения), должна быть плоскостью общего положения, что нарушит ортогональность плоскостей проекций в новой системе.
Преобразование плоскости общего положения, заданной следами, в проецирующую плоскость
В случае задания плоскости следами (рис. 118) для перевода ее из общего положения в проецирующее необходимо, чтобы один из заданных следов на эпюре стал перпендикулярен к оси 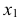 новой ортогональной системы
новой ортогональной системы 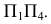 Тогда в этой системе плоскость займет проецирующее положение относительно
Тогда в этой системе плоскость займет проецирующее положение относительно 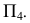
На рис. 118 ось 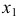 проведена перпендикулярно следу
проведена перпендикулярно следу 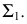 В этом случае для определения направления нового следа
В этом случае для определения направления нового следа 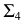 достаточно взять произвольную точку
достаточно взять произвольную точку 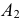 на следе
на следе 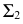 и указать ее проекцию на новой плоскости
и указать ее проекцию на новой плоскости 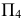 в соответствии с правилами построения, изложенными ранее. В новой системе
в соответствии с правилами построения, изложенными ранее. В новой системе 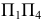 плоскость
плоскость 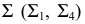 займет проецирующее положение относительно
займет проецирующее положение относительно 
Способ плоскопараллельного перемещения
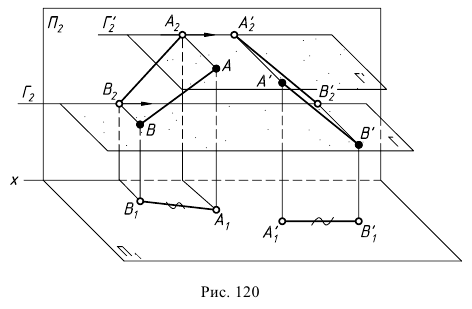
Сущность способа заключается в том, что все точки геометрического образа, меняющего свое положение в пространстве, перемещаются в плоскостях, параллельных одной из плоскостей проекций (рис. 119, а, 6), по произвольным траекториям.
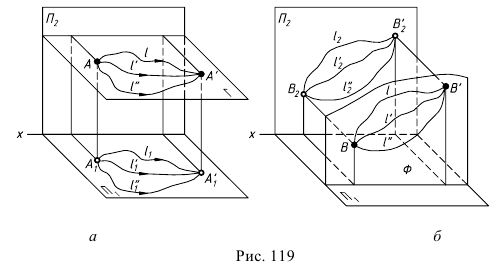
При параллельном переносе ортогональная проекция г.о. на плоскость, параллельно которой происходит перемещение его точек, сохраняет свои размеры и форму, изменяя лишь положение относительно оси проекций (справедливость этого утверждения при необходимости может быть легко доказана). Проекции всех точек г.о. на другой плоскости проекций перемещаются по прямым линиям, параллельным оси проекций и являющимися следами плоскостей перемещения.
Например, на рис. 120 прямая  в результате перемещения заняла положение параллельное
в результате перемещения заняла положение параллельное 
Произвольный перенос одной из проекций в новое положение позволяет избегать наложения проекций.
Преобразование прямой общего положения в прямую уровня и в проецирующую прямую
Пусть дана прямая  общего положения. Переведем ее сначала в положение фронтали, а затем в горизонтально-проецирующее положение (рис. 121).
общего положения. Переведем ее сначала в положение фронтали, а затем в горизонтально-проецирующее положение (рис. 121).
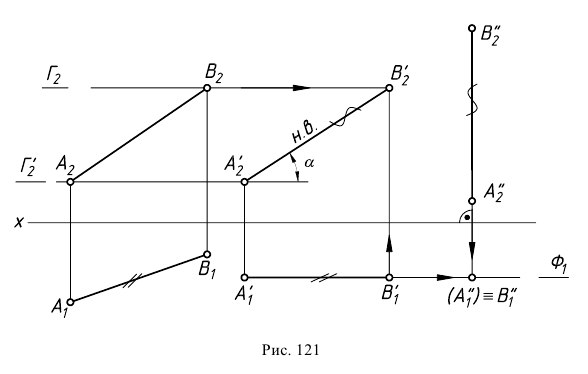
Первое преобразование. Точки  и
и  перемещаются в горизонтальных плоскостях уровня
перемещаются в горизонтальных плоскостях уровня  и
и 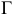 соответственно.
соответственно.
На эпюре после переноса горизонтальная проекция отрезка 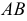 в соответствии с условиями преобразования сохраняет свою величину
в соответствии с условиями преобразования сохраняет свою величину 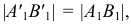 но становится параллельной оси проекций.
но становится параллельной оси проекций.
Фронтальная проекция 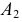 точки
точки 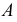 перемещается по следу плоскости перемещения
перемещается по следу плоскости перемещения 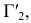 а проекция
а проекция 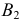 - по следу
- по следу 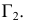
Новое положение проекций 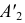 и
и 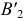 находят на пересечении линий проекционной связи, проходящих через
находят на пересечении линий проекционной связи, проходящих через 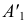 и
и 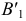 со следами соответствующих плоскостей. Проекция
со следами соответствующих плоскостей. Проекция 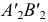 будет натуральной величиной отрезка
будет натуральной величиной отрезка 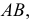 а угол
а угол 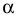 является углом наклона прямой
является углом наклона прямой 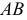 к плоскости проекций
к плоскости проекций 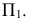
Второе преобразование. Фронтальную проекцию 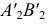 перенесем в новое положение, перпендикулярное оси
перенесем в новое положение, перпендикулярное оси 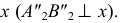 При этом точки
При этом точки 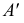 и
и 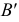 будут перемещаться во фронтальной плоскости уровня
будут перемещаться во фронтальной плоскости уровня 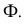 На следе этой плоскости
На следе этой плоскости 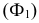 будет располагаться новая горизонтальная проекция прямой - точка
будет располагаться новая горизонтальная проекция прямой - точка 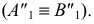
Преобразование плоскости общего положения в проецирующую плоскость и в плоскость уровня
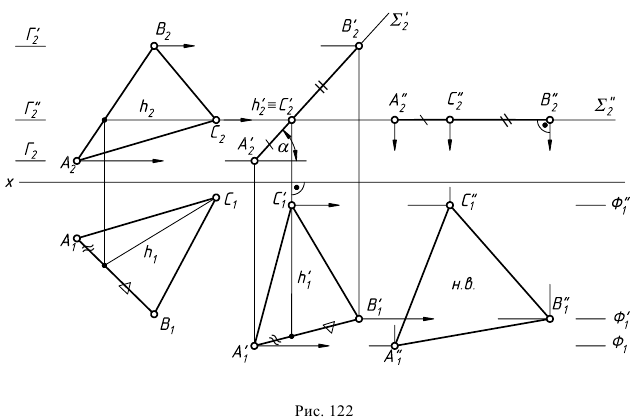
Рис. 122 дает полное представление о геометрических построениях, выполненных в результате этих преобразований. Перемещение точек плоскости 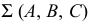 вначале производим в плоскостях
вначале производим в плоскостях 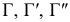 соответственно, параллельных
соответственно, параллельных  (перевод во фронтально-проецирующее положение), а затем в плоскостях
(перевод во фронтально-проецирующее положение), а затем в плоскостях 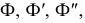 параллельных
параллельных 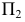 (горизонтальное положение уровня).
(горизонтальное положение уровня).
При первом перемещении проекцию 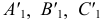 располагаем так, чтобы проекция горизонтали
располагаем так, чтобы проекция горизонтали 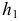 плоскости стала перпендикулярна оси
плоскости стала перпендикулярна оси 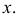 При втором перемещении след размещаем параллельно оси
При втором перемещении след размещаем параллельно оси 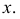
Способ вращения
Способ вращения заключается в том, что г.о. вращается в пространстве вокруг выбранной оси до требуемого положения относительно плоскостей проекций. Точки вращаемого предмета описывают в пространстве дуги окружностей, лежащих в плоскостях, перпендикулярных к оси вращения, а центры этих окружностей располагаются на оси вращения в точках пересечения оси с плоскостями. В качестве осей вращения можно применять либо проецирующие прямые, либо линии уровня.
Вращение вокруг оси, перпендикулярной плоскости проекции
Такое вращение является частным случаем параллельного перемещения, рассмотренного выше. Отличие состоит лишь в том, что траекториями перемещения точек в плоскостях, параллельных плоскости проекции, будут не произвольные линии, а окружности.
Проследим, как будет изменяться положение точки 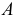 при этом способе перемещения (рис. 123).
при этом способе перемещения (рис. 123).
При вращении вокруг оси, перпендикулярной горизонтальной плоскости проекции  точка
точка 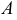 (см. рис. 123, а) будет перемещаться по дуге окружности
(см. рис. 123, а) будет перемещаться по дуге окружности 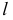 в плоскости
в плоскости 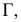 параллельной
параллельной 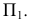 На эпюре (см. рис. 123, 6) эта окружность проецируется на плоскость
На эпюре (см. рис. 123, 6) эта окружность проецируется на плоскость 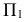 без искажения, а на плоскость
без искажения, а на плоскость 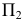 в отрезок прямой, параллельной оси
в отрезок прямой, параллельной оси 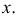
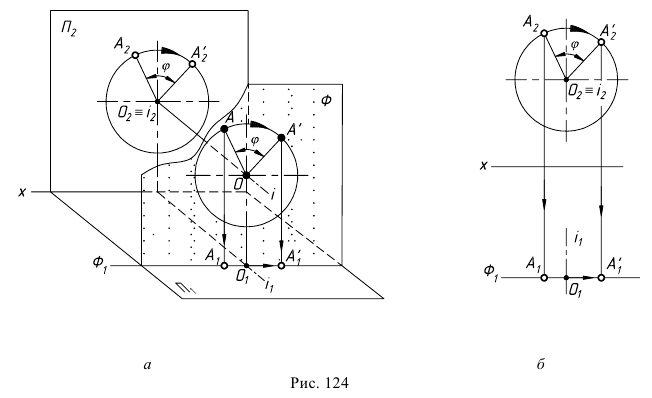
Вращение точки вокруг оси, перпендикулярной фронтальной плоскости проекций 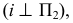 иллюстрирует рис. 124, а. Здесь точка
иллюстрирует рис. 124, а. Здесь точка 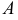 перемещается в новое положение
перемещается в новое положение 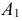 по окружности, лежащей в плоскости
по окружности, лежащей в плоскости 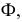 перпендикулярной оси вращения
перпендикулярной оси вращения 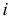 и параллельной
и параллельной 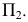 На эпюре (рис. 124, б) фронтальная проекция точки
На эпюре (рис. 124, б) фронтальная проекция точки 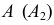 будет перемещаться по окружности с центром на фронтальной проекции оси вращения, а горизонтальная - по прямой
будет перемещаться по окружности с центром на фронтальной проекции оси вращения, а горизонтальная - по прямой 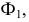 параллельной оси
параллельной оси 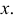
Выяснив характер перемещения проекций точки при вращении ее вокруг проецирующих прямых, можно осуществить перемещение проекций любой геометрической фигуры при переводе ее из заданного положения в частное.
Вращение отрезка прямой до положения линии уровня и проецирующего положения
При выполнении вращения ось можно проводить либо в произвольном месте, либо через одну из точек прямой. В последнем случае решение задачи облегчается, так как будет достаточно переместить лишь одну точку прямой, не лежащую на оси вращения.
Первое вращение. В зависимости от выбора оси вращения ( или
или  ) прямую общего положения можно перевести соответственно в положение фронтали или горизонтали.
) прямую общего положения можно перевести соответственно в положение фронтали или горизонтали.
На рис. 125 показаны построения, выполненные при перемещении отрезка  общего положения, в положение, параллельное
общего положения, в положение, параллельное  Ось вращения в этом случае будет перпендикулярна
Ось вращения в этом случае будет перпендикулярна  Проведем ее через точку
Проведем ее через точку  На эпюре горизонтальная проекция точки
На эпюре горизонтальная проекция точки  перемещается по дуге в положение
перемещается по дуге в положение 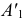 так, чтобы
так, чтобы 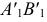 стала параллельна оси проекций
стала параллельна оси проекций 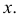 При этом фронтальная проекция
При этом фронтальная проекция 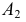 переместится по следу горизонтальной плоскости уровня и займет положение в точке пересечения следа
переместится по следу горизонтальной плоскости уровня и займет положение в точке пересечения следа 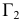 и линии связи, восстановленной из
и линии связи, восстановленной из 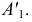 Соединив
Соединив 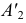 и
и 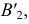 получим фронтальную проекцию фронтали
получим фронтальную проекцию фронтали 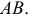
Второе вращение. Вращение фронтали 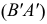 при переводе ее в положение горизонтально-проецирующей прямой осуществляется вокруг фронтально-проецирующей оси
при переводе ее в положение горизонтально-проецирующей прямой осуществляется вокруг фронтально-проецирующей оси 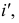 проходящей через точку
проходящей через точку 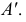
На эпюре (см. рис. 125) фронтальная проекция оси вращения 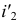 совпадет с проекциями
совпадет с проекциями 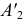 и
и 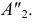 Новое положение проекции
Новое положение проекции 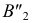 получим, повернув
получим, повернув 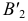 вокруг
вокруг 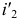 до положения отрезка
до положения отрезка 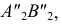 перпендикулярного оси
перпендикулярного оси 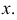 Горизонтальная проекция точки
Горизонтальная проекция точки 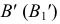 переместится по следу
переместится по следу 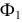 и займет новое положение
и займет новое положение 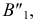 совпадающее с
совпадающее с 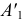 и
и 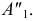
Вращение плоскости общего положения до проецирующего и положения плоскости уровня
На рис. 126 плоскость общего положения  задана
задана  В том случае, когда требуется определить истинную величину плоской фигуры, заданной в общем положении, необходимо осуществить два последовательных вращения вокруг осей, перпендикулярных вначале одной плоскости проекций, а затем другой. Предварительно в плоскости
В том случае, когда требуется определить истинную величину плоской фигуры, заданной в общем положении, необходимо осуществить два последовательных вращения вокруг осей, перпендикулярных вначале одной плоскости проекций, а затем другой. Предварительно в плоскости 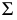 проводится горизонталь
проводится горизонталь 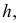 и затем плоскость вращается вокруг оси
и затем плоскость вращается вокруг оси 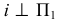 до тех пор, пока горизонталь не будет перпендикулярна плоскости
до тех пор, пока горизонталь не будет перпендикулярна плоскости 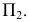 При этом плоскость общего положения станет фронтально-проецирующей.
При этом плоскость общего положения станет фронтально-проецирующей.
Второе вращение плоскости 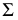 осуществляется вокруг оси
осуществляется вокруг оси 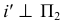 до положения, параллельного плоскости
до положения, параллельного плоскости 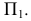 В результате этого вращения фронтально-проецирующая плоскость
В результате этого вращения фронтально-проецирующая плоскость 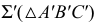 станет горизонтальной плоскостью уровня и спроецируется на
станет горизонтальной плоскостью уровня и спроецируется на 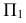 в натуральную величину
в натуральную величину 
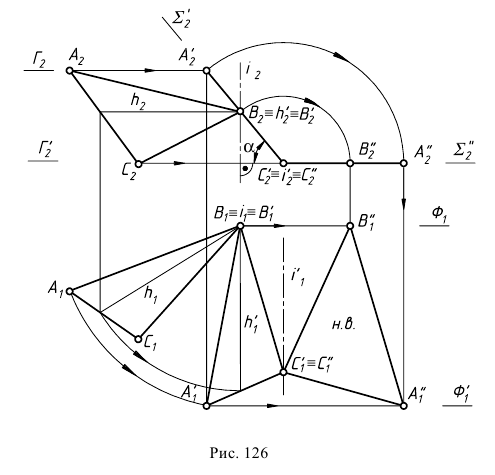
Вращение вокруг линии уровня
Этот способ является эффективным приемом, упрощающим решение задач на определение натуральной величины плоской фигуры. Путем вращения вокруг линии уровня можно сразу повернуть плоскость до положения, параллельного плоскости проекции.
При таком повороте каждая точка г.о. перемещается по своей окружности, расположенной в плоскости, перпендикулярной оси вращения. Центр окружностей будет находиться на оси вращения, а величина радиуса вращения будет равна расстоянию от точки до оси вращения.
Если за ось вращения взята горизонталь (рис. 127, а), то окружность, по которой движется точка, будет проецироваться на  в отрезок прямой, перпендикулярной горизонтальной проекции оси
в отрезок прямой, перпендикулярной горизонтальной проекции оси 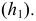 На плоскости
На плоскости 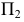 окружность проецируется в эллипс, построение которого можно не выполнять.
окружность проецируется в эллипс, построение которого можно не выполнять.
Анализируя рис. 127, а, можно прокомментировать построения, выполняемые на плоскости 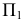 при перемещении т.
при перемещении т. 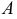 по окружности, плоскость которой перпендикулярна оси вращения
по окружности, плоскость которой перпендикулярна оси вращения 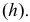 Сначала необходимо найти положение центра вращения и определить натуральную величину радиуса вращения. Проекция
Сначала необходимо найти положение центра вращения и определить натуральную величину радиуса вращения. Проекция 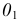 центра вращения находится в точке пересечения проекции оси вращения
центра вращения находится в точке пересечения проекции оси вращения 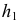 с горизонтальным следом плоскости
с горизонтальным следом плоскости 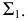
Для нахождения величины радиуса вращения используется способ треугольника. Строим на плоскости 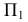 прямоугольный треугольник, один катет которого - проекция радиуса
прямоугольный треугольник, один катет которого - проекция радиуса 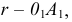 а другой - разница аппликаты концов отрезка
а другой - разница аппликаты концов отрезка 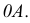 Гипотенуза
Гипотенуза 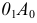 будет натуральной величиной
будет натуральной величиной 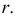
Новое, после поворота, положение точки 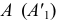 будет находиться на следе плоскости
будет находиться на следе плоскости  в месте, удаленном от точки
в месте, удаленном от точки 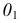 на величину натурального радиуса
на величину натурального радиуса 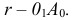
Полный эпюр точки 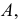 перемещающейся вокруг горизонтали
перемещающейся вокруг горизонтали 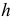 в положение
в положение 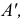 показан на рис. 127, б.
показан на рис. 127, б.
Построения аналогичны (рис. 128), если за ось вращения выбрана фронталь. В этом случае траектория перемещения точки будет проецироваться на  в виде отрезка прямой, перпендикулярной фронтальной проекции фронтали. Эта прямая есть след плоскости вращения
в виде отрезка прямой, перпендикулярной фронтальной проекции фронтали. Эта прямая есть след плоскости вращения  Центр вращения
Центр вращения 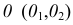 находится как точка пересечения
находится как точка пересечения 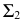 с фронтальной проекцией фронтали
с фронтальной проекцией фронтали 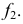 Определив натуральную величину радиуса вращения
Определив натуральную величину радиуса вращения 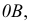 можно найти новое положение точки
можно найти новое положение точки 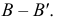
Пример решения задачи на нахождение н.в. плоской фигуры этим способом приведен в разделе IV.4, задача 3.
Дополнительные сведения
Способ вращения вокруг горизонтали или фронтали включает в себя и вращение вокруг линии нулевого уровня (следа плоскости). При таком вращении плоскость общего положения после поворота совпадает (совмещается) с плоскостью проекций, поэтому этот способ называют способом совмещения. Совмещение, так же как и вращение, вокруг линии уровня, применяется в тех случаях, когда требуется определить натуральный вид фигур, лежащих в плоскости общего положения.
Сущность способа совмещения проиллюстрирована на рис. 129.
На рис. 129, а показаны построения, выполненные при совмещении точки 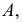 лежащей на следе плоскости
лежащей на следе плоскости 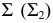 с плоскостью
с плоскостью 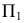 поворотом вокруг
поворотом вокруг 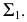 Последовательность построений видна из рисунка.
Последовательность построений видна из рисунка.
Анализируя рис. 129, а, можно видеть, что не обязательно пользоваться построениями центра и радиуса вращения, а нужно лишь отметить на следе 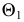 плоскости, в которой происходит поворот, отрезок, равный
плоскости, в которой происходит поворот, отрезок, равный 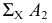 (см. рис. 129, б). Через построенную проекцию точки
(см. рис. 129, б). Через построенную проекцию точки 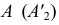 идет искомый след плоскости
идет искомый след плоскости 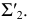
Примеры решения задач способами преобразования чертежа
Задача 1. Определить расстояние от точки до прямой (рис. 130). Заданы прямая общего положения  и точка
и точка  Задача в общем виде решена в разделе III.5 (задача 1). В данном случае применяется способ перемены плоскостей проекций. При решении задачи следует руководствоваться следующими рассуждениями:
Задача в общем виде решена в разделе III.5 (задача 1). В данном случае применяется способ перемены плоскостей проекций. При решении задачи следует руководствоваться следующими рассуждениями:
- - расстояние от точки до прямой определяется перпендикуляром, опущенным из этой точки на данную прямую;
- - заданная прямая
 занимает общее положение, поэтому прямой угол между данной прямой и перпендикуляром, проведенным к ней, проецируется на плоскости проекций с искажением.
занимает общее положение, поэтому прямой угол между данной прямой и перпендикуляром, проведенным к ней, проецируется на плоскости проекций с искажением.
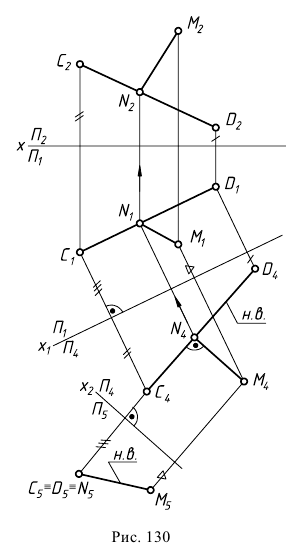
Для того чтобы прямой угол спроецировался в натуральную величину, одна сторона его должна быть линией уровня согласно теореме о проецировании прямого угла. Поэтому прямую общего положения  необходимо преобразовать в линию уровня проецированием на дополнительную плоскость проекций
необходимо преобразовать в линию уровня проецированием на дополнительную плоскость проекций  Таким образом, первая замена плоскости проекций необходима для построения прямого угла. Вторую перемену плоскости проекций выполняют для нахождения н.в. искомого расстояния. На рис. 130 первая дополнительная плоскость проекций
Таким образом, первая замена плоскости проекций необходима для построения прямого угла. Вторую перемену плоскости проекций выполняют для нахождения н.в. искомого расстояния. На рис. 130 первая дополнительная плоскость проекций  параллельна прямой
параллельна прямой 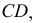 т.е. ось
т.е. ось 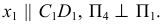 На новой плоскости проекций
На новой плоскости проекций 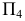 строят н.в.
строят н.в. 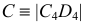 и точку
и точку 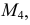 из которой опускается перпендикуляр к
из которой опускается перпендикуляр к 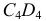 (прямой угол на плоскости
(прямой угол на плоскости 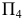 изобразится в н.в.). Находят недостающие проекции точки
изобразится в н.в.). Находят недостающие проекции точки 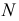 -основания перпендикуляра.
-основания перпендикуляра.
Для определения длины отрезка перпендикуляра 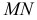 необходимо преобразовать его в линию уровня. Вводят еще одну дополнительную плоскость проекций
необходимо преобразовать его в линию уровня. Вводят еще одну дополнительную плоскость проекций 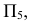 которая параллельна
которая параллельна 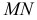 и перпендикулярна
и перпендикулярна 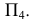 На эпюре
На эпюре 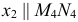 и
и 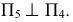
На плоскости проекций 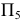 проекция
проекция 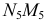 будет натуральной величиной искомого перпендикуляра: н.в.
будет натуральной величиной искомого перпендикуляра: н.в. 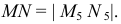
Задача 2. Определить расстояние между параллельными прямыми (рис. 131).
Заданы параллельные прямые общего положения 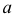 и
и 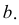 Расстояние между параллельными прямыми определяется перпендикуляром, проведенным из произвольной точки, взятой на одной прямой, к другой прямой. Для построения проекций этого перпендикуляра следует заданные параллельные прямые
Расстояние между параллельными прямыми определяется перпендикуляром, проведенным из произвольной точки, взятой на одной прямой, к другой прямой. Для построения проекций этого перпендикуляра следует заданные параллельные прямые 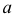 и
и 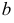 проецированием на дополнительную плоскость проекций
проецированием на дополнительную плоскость проекций 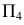 преобразовать в прямые уровня. Для определения н.в. перпендикуляра выполняют вторую перемену плоскости проекций так, чтобы перпендикуляр преобразовать в линию уровня.
преобразовать в прямые уровня. Для определения н.в. перпендикуляра выполняют вторую перемену плоскости проекций так, чтобы перпендикуляр преобразовать в линию уровня.
На рис. 131 плоскость 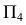 выбирают параллельно прямым
выбирают параллельно прямым 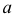 и
и 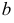 и перпендикулярно
и перпендикулярно 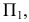 т.е.
т.е. 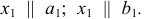 Строят проекции параллельных прямых
Строят проекции параллельных прямых 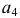 и
и 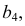 , которые в новой системе плоскостей станут прямыми уровня относительно
, которые в новой системе плоскостей станут прямыми уровня относительно 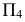 и спроецируются на
и спроецируются на 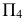 в натуральную величину.
в натуральную величину.
На проекции прямой 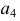 выбирают произвольную точку
выбирают произвольную точку 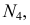 из которой проводят проекции перпендикуляра
из которой проводят проекции перпендикуляра 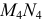 к
к 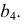 Строят горизонтальную и фронтальную проекции перпендикуляра
Строят горизонтальную и фронтальную проекции перпендикуляра 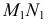 и
и 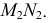 Для определения н.в. отрезка перпендикуляра
Для определения н.в. отрезка перпендикуляра 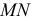 вводят дополнительную плоскость проекций
вводят дополнительную плоскость проекций 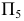 параллельно
параллельно 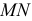 и перпендикулярно
и перпендикулярно 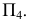 Таким образом, расстояние между параллельными прямыми
Таким образом, расстояние между параллельными прямыми 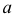 и
и 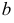 будет равно отрезку перпендикуляра
будет равно отрезку перпендикуляра 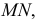 натуральная величина которого изображена на
натуральная величина которого изображена на 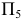 и равна
и равна 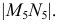
Задача 3. Построить натуральную величину плоской фигуры способом вращения вокруг линии уровня (рис. 132).
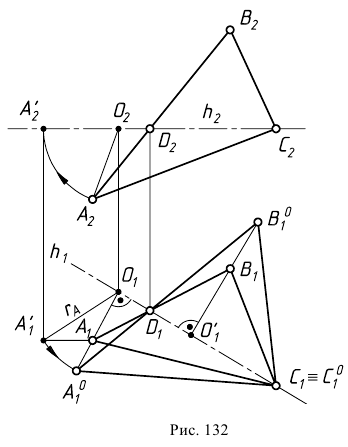
Задана  - плоскость общего положения.
- плоскость общего положения.
Определить натуральную величину 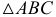 можно при повороте его вокруг горизонтали данной плоскости до положения параллельного
можно при повороте его вокруг горизонтали данной плоскости до положения параллельного 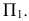 При этом расстояние от каждой перемещающейся вершины до оси вращения, равное радиусу вращения данной точки, на
При этом расстояние от каждой перемещающейся вершины до оси вращения, равное радиусу вращения данной точки, на 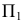 проецируется без искажения.
проецируется без искажения.
При повороте плоскости в новое положение вокруг горизонтали 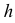 будут перемещаться только две вершины (
будут перемещаться только две вершины (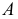 и
и 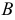 ) треугольника, которым и задана плоскость
) треугольника, которым и задана плоскость 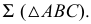 Вершина
Вершина 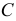 остается неподвижной, так как принадлежит оси вращения.
остается неподвижной, так как принадлежит оси вращения.
Необходимые геометрические построения на эпюре выполняют в следующей последовательности:
1) строят проекции горизонтали 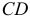 в данной плоскости;
в данной плоскости;
2) находят центры вращения точек 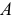 и
и 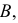 для чего из точек
для чего из точек 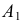 и
и 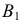 проводят прямые, перпендикулярные
проводят прямые, перпендикулярные 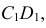 по которым будут перемещаться горизонтальные проекции вращающихся точек. Пересечение прямых с осью даст
по которым будут перемещаться горизонтальные проекции вращающихся точек. Пересечение прямых с осью даст  (в данном примере центр
(в данном примере центр 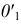 можно не использовать);
можно не использовать);
3) строят фронтальную проекцию радиуса вращения точки 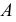 - отрезок
- отрезок 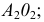
4) определяют натуральную величину радиуса вращения 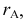 вращая отрезок
вращая отрезок 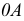 вокруг оси, проходящей через точку
вокруг оси, проходящей через точку 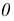 и перпендикулярной
и перпендикулярной 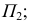
5) отрезок 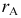 откладывают от точки
откладывают от точки 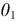 вдоль той прямой, по которой перемещается горизонтальная проекция вершины
вдоль той прямой, по которой перемещается горизонтальная проекция вершины 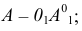
6) через полученную точку 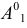 и неподвижную
и неподвижную 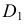 проводят прямую до пересечения в точке
проводят прямую до пересечения в точке 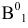 с прямой, по которой перемещается горизонтальная проекция вершины
с прямой, по которой перемещается горизонтальная проекция вершины 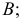
7) соединяя найденные точки 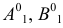 друг с другом и с неподвижной вершиной
друг с другом и с неподвижной вершиной 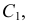 получают новую горизонтальную проекцию треугольника, которая определяет натуральную величину
получают новую горизонтальную проекцию треугольника, которая определяет натуральную величину  Фронтальная проекция треугольника окажется преобразованной в прямую, совпадающую с
Фронтальная проекция треугольника окажется преобразованной в прямую, совпадающую с 
Задача 4. Определить расстояние от точки до плоскости общего положения способом плоскопараллельного перемещения (рис. 133).
Для решения задачи плоскость общего положения необходимо преобразовать в проецирующую плоскость. В этом случае искомое расстояние будет проекцией перпендикуляра, опущенного из заданной точки на след плоскости.
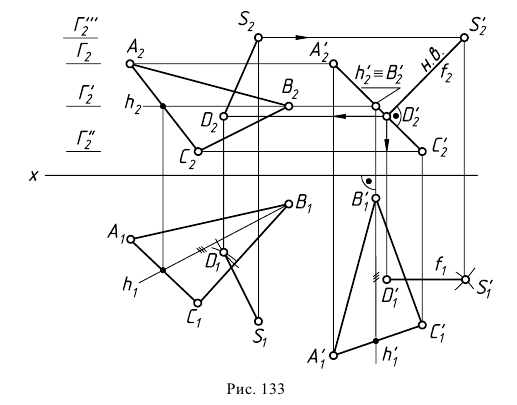
Заданную плоскость  преобразуют во фронтально-проецирующую плоскость, при этом перпендикуляр
преобразуют во фронтально-проецирующую плоскость, при этом перпендикуляр 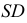 к плоскости будет фронталью
к плоскости будет фронталью 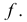
При перемещении (см. рис. 133) горизонтальная проекция плоскости займет новое положение, при котором проекция ее горизонтали станет перпендикулярна оси 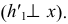 Сама проекция треугольника
Сама проекция треугольника 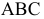 при этом не изменится
при этом не изменится 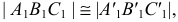 сохранится также и положение точки
сохранится также и положение точки 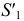 относительно точек
относительно точек 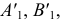 и
и 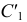 (точка
(точка  строится с помощью циркуля на пересечении дуг радиусом
строится с помощью циркуля на пересечении дуг радиусом 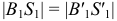 и
и 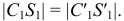
Положение точки  (как и других точек
(как и других точек 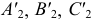 ) определяют по линии проекционной связи на следе
) определяют по линии проекционной связи на следе 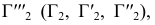 соответствующей плоскости уровня, в которой она перемещается.
соответствующей плоскости уровня, в которой она перемещается.
Далее строят проекции перпендикуляра, опущенного из точки  на плоскость
на плоскость  проведя
проведя 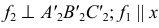 и находят проекции
и находят проекции 
 его основания.
его основания.
Выполняя «обратное» плоскопараллельное перемещение, строят  (применяя засечки для нахождения
(применяя засечки для нахождения 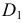 ) и
) и 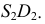
Задача 5. Построить плоскость, параллельную плоскости общего положения и удаленную от нее на заданное расстояние (рис. 134).
Истинную величину расстояния между параллельными плоскостями можно увидеть, если они занимают проецирующее положение. Поэтому
для решения задачи преобразуем заданную плоскость 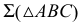 в проецирующую и, отмерив по перпендикуляру от следа
в проецирующую и, отмерив по перпендикуляру от следа 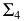 натуральную величину расстояния
натуральную величину расстояния 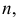 сможем провести след искомой параллельной плоскости
сможем провести след искомой параллельной плоскости 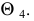 Останется перенести любую точку этой плоскости из системы
Останется перенести любую точку этой плоскости из системы 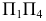 в систему
в систему 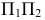 и через нее уже в этой системе построить модель параллельной плоскости. На эпюре выполняются следующие построения:
и через нее уже в этой системе построить модель параллельной плоскости. На эпюре выполняются следующие построения:
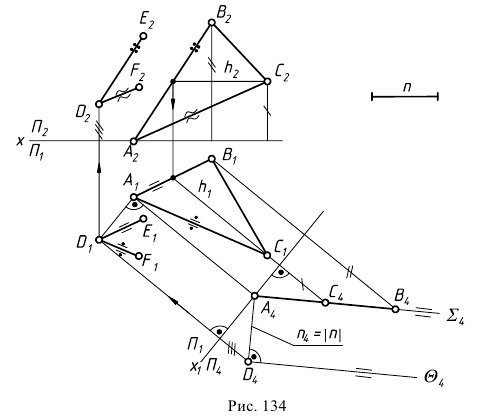
1) строится проекция заданной плоскости  на плоскость проекций
на плоскость проекций  Это прямая
Это прямая 
2) от точки  (или любой другой точки) на перпендикуляре к
(или любой другой точки) на перпендикуляре к  откладывается отрезок
откладывается отрезок  Через полученную точку
Через полученную точку  проводится след
проводится след  искомой плоскости
искомой плоскости 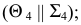
3) строится горизонтальная проекция отрезка 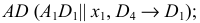
4) находится фронтальная проекция  точки
точки  преобразованием обратным первому;
преобразованием обратным первому;
5) через  и
и  проводятся одноименные проекции параллельных соответствующим сторонам треугольника пересекающихся прямых
проводятся одноименные проекции параллельных соответствующим сторонам треугольника пересекающихся прямых 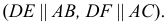
Задача имеет два решения, т.к. искомую плоскость можно разместить по разные стороны от заданной плоскости. На эпюре показано одно решение.
Способы преобразования комплексного чертежа
Преобразование комплексного чертежа - это способы перехода от общих положений прямой и плоскости в системе 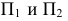 к частным в той же или дополнительной системе.
к частным в той же или дополнительной системе.
Существует два способа преобразования чертежа прямой линии или плоской фигуры общего положения в чертеж с их частным положением.
- Заменяют заданную систему плоскостей проекций на новую так, чтобы относительно их исходные объекты оказались в частном положении, не меняя своего расположения в пространстве - способ перемены плоскостей проекции.
- Изменяют положение исходных объектов в пространстве так, чтобы они приняли частное положение относительно плоскостей проекций - способ вращения.
Способ перемены плоскостей проекций
Заключается в следующем: положение точек, линий, плоских фигур, поверхностей в пространстве не изменяется, а система 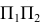 дополняется плоскостями, образующими с
дополняется плоскостями, образующими с  между собой системы двух взаимно- перпендикулярных плоскостей, принимаемых за плоскости проекций.
между собой системы двух взаимно- перпендикулярных плоскостей, принимаемых за плоскости проекций.
Если задача дана на преобразование прямой, то её делают сначала прямой уровня, а затем - проецирующей.
Если задача на плоскость - плоскость сначала делается проецирующей, а затем - уровня.
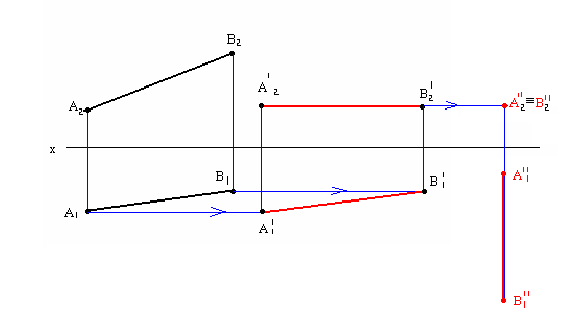
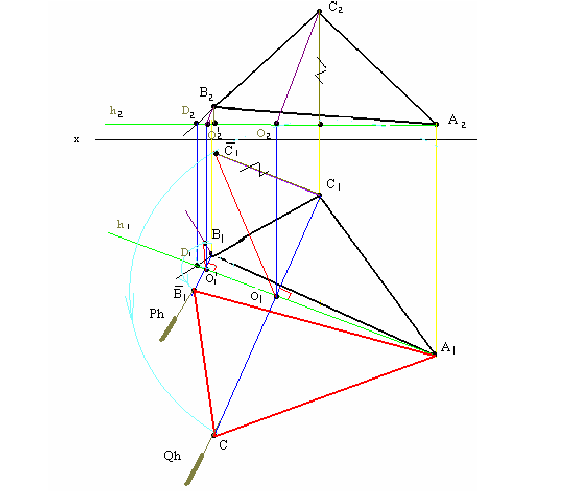
1. Определить НВ прямой AВ 2.Привести отрезок прямой общего положения в проецирующее положение
1. Плоскость 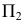 заменяем на новую плос кость
заменяем на новую плос кость 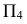 перпендикулярную
перпендикулярную 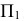 // АВ. Тогда новая ось
// АВ. Тогда новая ось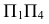 будет//
будет//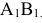
Расстояние от оси 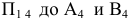 равно соответственно расстоянию от
равно соответственно расстоянию от  до оси
до оси  . (т.е. расстояние до оси замеряем на той плоскости, которую заменяем).
. (т.е. расстояние до оси замеряем на той плоскости, которую заменяем).
2. Получили прямую в натуральную величину (сделали АВ прямой уровня). Заменяем 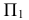 на
на 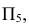 перпендикулярную
перпендикулярную 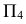 и перпендикулярную АВ. Тогда новая ось
и перпендикулярную АВ. Тогда новая ось 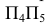 будет перпендикулярна
будет перпендикулярна 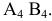 От оси
От оси 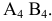 по линиям связи, проведенным с
по линиям связи, проведенным с 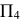 на
на 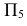 откладываем расстояния, равные расстояниям от
откладываем расстояния, равные расстояниям от 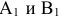 до оси
до оси 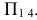 . АВ на
. АВ на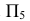 спроецировалось в точку
спроецировалось в точку 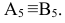
Сделать 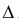 AВС проецирующим
AВС проецирующим
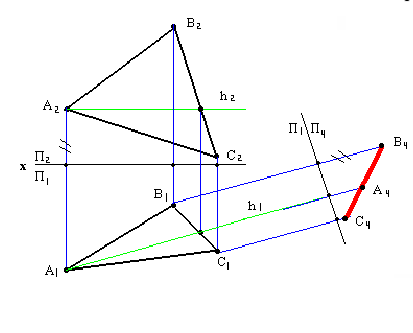
Вводим дополнительную плоскость, перпендикулярную плоскости треугольника АВС (надо ввести плоскость перпендикулярно любой прямой в плоскости треугольника -горизонтали или фронтали). От системы  переходим к системе
переходим к системе  перпендикулярно
перпендикулярно  и перпендикулярна
и перпендикулярна  АВС (проводим горизонталь
АВС (проводим горизонталь 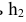 // оси X и по линиям связи -
// оси X и по линиям связи - 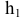 ). Новая плоскость
). Новая плоскость 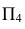 перпендикулярна h (ось
перпендикулярна h (ось 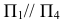 перпендикулярна
перпендикулярна  и соответственно
и соответственно  ).
).
Производим две замены.
Определить расстояние от точки A до прямой ВС
ВС делаем проецирующей. 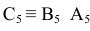 - расстояние искомое.
- расстояние искомое.
Определить расстояние между двумя параллельными прямыми
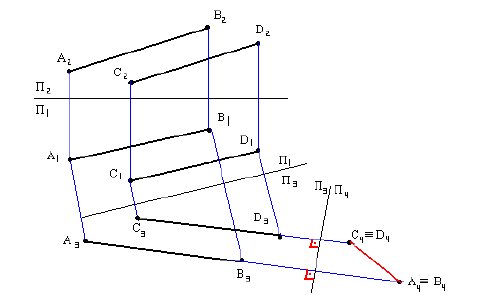
Прямые необходимо сделать проецирующими.
Определить расстояние между скрещивающимися прямыми
Вращение вокруг проецирующей прямой
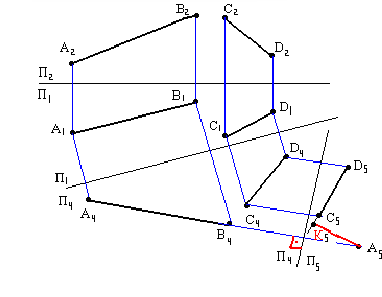
Способ вращения
Через точку А проводим вертикальную ось i, вокруг которой поворачиваем отрезок до положения, параллельного фронтальной плоскости проекций -
он займет положение
Способ вращения
Через точку А проводим вертикальную ось i, вокруг которой поворачиваем отрезок до положения, параллельного фронтальной плоскости проекций -
он займет положение 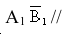 оси X. На пересечении линии связи из
оси X. На пересечении линии связи из 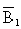 ! с прямой, проведенной из
! с прямой, проведенной из
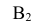 // оси X получим
// оси X получим 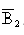 . Отрезок
. Отрезок  - есть НВ отрезка АВ.
- есть НВ отрезка АВ.
Плоскопараллельное перемещение
Плоскопараллельным называется такое движение фигуры в пространстве, при котором все её точки перемещаются в плоскостях, // между собой и // одной из плоскостей проекций оси X. На пересечении линии связи из Е-! с прямой, проведенной из
В: // оси X получим В2. Отрезок А2Ё2 - есть НВ отрезка АВ.
Плоскопараллельное перемещение
Плоскопараллельным называется такое движение фигуры в пространстве, при котором все её точки перемещаются в плоскостях, // между собой и // одной из плоскостей проекций.
АВ перемещаем //  до положения, при котором отрезок станет //
до положения, при котором отрезок станет // 
Для этого фронтальную проекцию 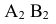 не изменяя её величины располагают на свободном поле чертежа на
не изменяя её величины располагают на свободном поле чертежа на 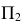 // оси X. Из горизонтальной проекции
// оси X. Из горизонтальной проекции 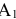 В проведем прямые,// оси X до пересечения с вертикальными линиями связи из
В проведем прямые,// оси X до пересечения с вертикальными линиями связи из 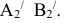
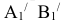 - НВ отрезка АВ.
- НВ отрезка АВ.
Чтобы теперь сделать этот отрезок проецирующим, расположим 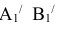 перпендикулярно
перпендикулярно 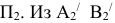 проведем прямые, параллельные оси X до пересечения с линиями связи из
проведем прямые, параллельные оси X до пересечения с линиями связи из 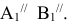
АВ спроецировалась в точку 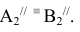
(Проекция фигуры на плоскости, относительно которой она перемещается, остается неизменной по своей величине и форме. А другие проекции точек этой фигуры перемещаются по прямым, параллельным оси X ).
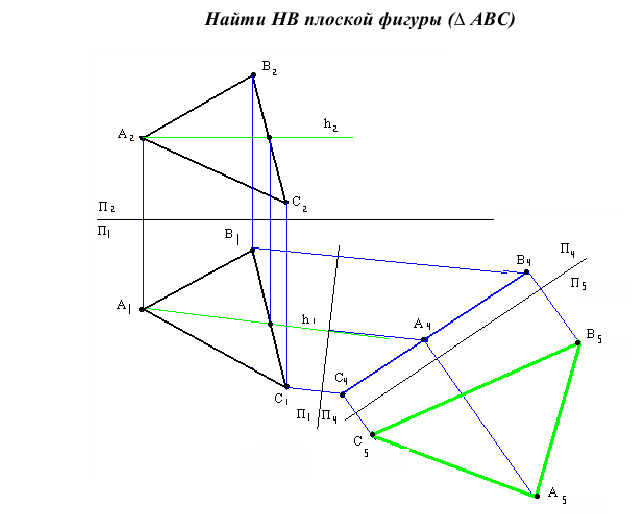
Найти НВ  АВС и определить расстояние от точки S до
АВС и определить расстояние от точки S до  АВС
АВС
1 .Разворачиваем 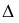 АВС в положение перпендикулярное
АВС в положение перпендикулярное 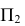 . Берм для этого горизонталь А1 и поворачиваем её перпендикулярно
. Берм для этого горизонталь А1 и поворачиваем её перпендикулярно 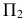 на свободном поле чертежа на
на свободном поле чертежа на 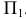 . Тогда
. Тогда 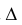 АВС, содержащий эту горизонталь, будет перпендикулярен
АВС, содержащий эту горизонталь, будет перпендикулярен 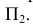
(Проекцию 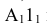 поворачиваем перпендикулярно оси X и строим
поворачиваем перпендикулярно оси X и строим 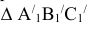 методом засечек. Этим же методом строим
методом засечек. Этим же методом строим 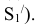
Проекции 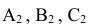 перемещаются по прямым // оси X. На пересечении этих прямых с линиями связи из
перемещаются по прямым // оси X. На пересечении этих прямых с линиями связи из 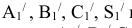 получаем точки
получаем точки 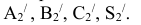
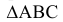 спроецировался в прямую
спроецировался в прямую 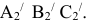
2. Поворачиваем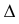 АВС //
АВС //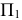 (ось вращения проходит через
(ось вращения проходит через 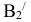 перпендикулярно
перпендикулярно 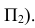 Фронтальная проекция
Фронтальная проекция  не изменяет вид и величину при повороте, т.е. поворачиваем
не изменяет вид и величину при повороте, т.е. поворачиваем  // ОХ. При этом точки
// ОХ. При этом точки 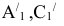 перемещаются по прямым, // ОХ.
перемещаются по прямым, // ОХ.
На пересечении этих прямых с линиями связи из 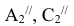 получаем точки
получаем точки 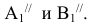
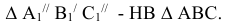
Вращение вокруг оси, параллельной плоскости проекции
Метод вращения - частный случай плоскопараллельного перемещения.
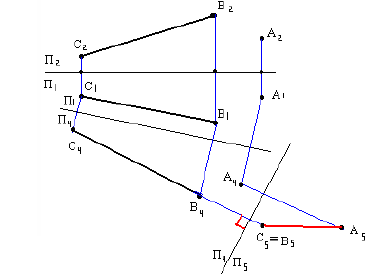
Найти НВ  АВС методом вращения вокруг горизонтали.
АВС методом вращения вокруг горизонтали.
Проводим горизонталь AD  Т.к. точка А лежит на горизонтали, то она остается неподвижной.
Т.к. точка А лежит на горизонтали, то она остается неподвижной.
Все точки (кроме лежащих на оси вращения) вращаются вокруг оси по окружностям в плоскостях, перпендикулярных к оси, пока треугольник не займет положение // плоскости проекций.
Рассмотрим вращение точки С. Для этого необходимо знать центр О  и радиус R вращения.
и радиус R вращения.
Центр вращения находим:
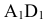 натуральная величина горизонтали, значит из
натуральная величина горизонтали, значит из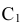 опускаем перпендикуляр на ось вращения AD
опускаем перпендикуляр на ось вращения AD 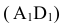 и получаем центр вращения О
и получаем центр вращения О 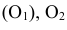 определяем по линии связи на
определяем по линии связи на 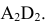
Радиус вращения определяем методом прямоугольного треугольника по катетам 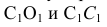 Строим прямоугольный
Строим прямоугольный 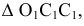 гипотенуза которого
гипотенуза которого 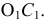
Находим положение точки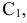 вращая
вращая 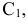 по окружности радиусом
по окружности радиусом 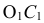 из центра
из центра 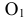 до пересечения с перпендикуляром, опущенным из
до пересечения с перпендикуляром, опущенным из 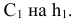
Преобразования комплексного чертежа
Способы преобразования комплексного чертежа позволяют переходить от произвольных положений пространственных объектов к частным по отношению к плоскостям проекций, что упрощает решение ряда позиционных и метрических задач.
Способ замены плоскостей проекций
Способ замены плоскостей проекций состоит в том, что проецируемый объект остается неподвижным, а одна из плоскостей проекций П1, П2 или П3 заменяется новой, расположенной так, чтобы проецируемый объект по отношению к новой плоскости занял частное положение. При этом каждая новая плоскость проекций должна быть перпендикулярна незаменяемой плоскости проекций.
Кроме того, на новые плоскости проекций объект проецируется ортогонально.
Таким образом, при решении задач способом замены плоскостей проекций необходимо выполнять следующие условия:
- каждая новая система должна представлять собой систему двух взаимно перпендикулярных плоскостей;
- на новые плоскости объект проецируется ортогонально;
- расстояние от точки до незаменяемой плоскости сохраняется.
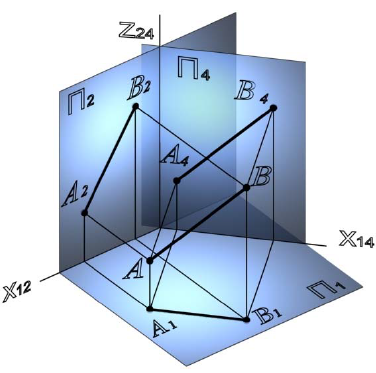
Рис. 11.1. Замена плоскостей проекций
Чтобы определить натуральную величину отрезка [AB ] способом замены плоскостей проекций (рис. 11.1, 11.2), необходимо выбрать новую плоскость проекций таким образом, чтобы в новой системе плоскостей проекций отрезок занял положение линии уровня:
- Зафиксировать положение системы плоскостей П1/П2 с помощью оси х12
 A1A2.
A1A2. - Определить положение плоскости П4 с помощью оси x14. Чтобы отрезок в системе плоскостей П1/П4 занял положение линии уровня, ось x14 проводится параллельно горизонтальной проекции отрезка [A1B1].
- Ортогонально спроецировать отрезок [AB] на плоскость П4. Для этого линии связи проводят перпендикулярно оси x14, затем от оси x14 откладывают расстояние до незаменяемой плоскости - координаты z точек A и B.
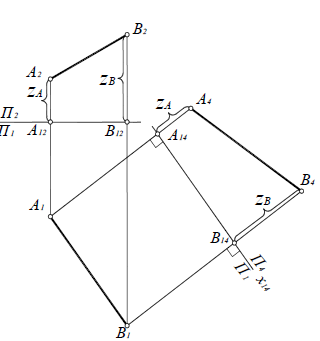
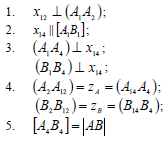
Рис. 11.2. Определение натуральной величины отрезка способом замены плоскостей проекций
Чтобы преобразовать плоскость общего положения в проецирующую, новую плоскость проекций строят перпендикулярно линии уровня этой плоскости.
Рассмотрим преобразование плоскости общего положения α(ABC) во фронтально-проецирующую плоскость (рис. 11.3). Для решения этой задачи способом замены плоскостей проекций необходимо выполнить замену плоскости П2 на П4:
- Зафиксировать положение системы плоскостей проекций П1/П2 с помощью оси x12
 A1A2;
A1A2; - Построить в плоскости α(ABC) фронталь;
- В соответствии с теоремой о проекциях прямого угла, построить новую ось X24

 1( C2 12);
1( C2 12); - Ортогонально спроецировать фронталь на плоскость П4. Для этого провести линию связи (12,14) перпендикулярно x24 и отложить от оси x24 расстояние до незаменяемой плоскости - координату у точек 1 и С. Поскольку y1=yс, фронталь в системе плоскостей проекций П1/П4 займет положение горизонтально-проецирующей прямой.
- Проекция плоскости α(ABC) на П4 определится фронталью и точкой A. В системе плоскостей проекций П2/П4 плоскость α(ABC) займет горизонтально-проецирующее положение. Проекцию точки B можно построить по координате yB или на пересечении следа плоскости α(ABC) на П4 с линией связи (B2B4).
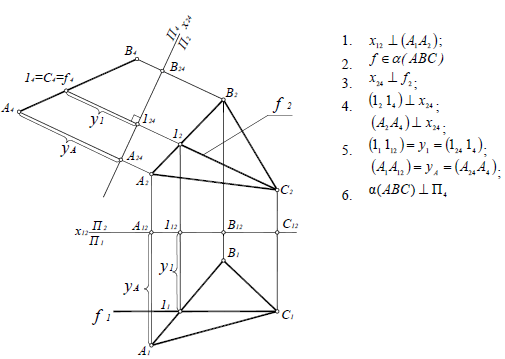
Рис. 11.3. Преобразование плоскости α(ABC) в проецирующее положение
При решении некоторых задач необходимо определить натуральную величину плоских объектов. Любой плоский объект проецируется без искажения на параллельную ему плоскость.
Чтобы определить натуральную величину грани призмы способом замены плоскостей проекций, необходимо (рис. 11.4):
- Зафиксировать положение системы плоскостей П1/П2 с помощью оси x12=A2D2K2;.
- Плоскость грани ABCD занимает горизонтально-проецирующее положение, поэтому выполняется замена плоскости П2 на плоскость П4, параллельную грани ABCD. Новую ось x14 проводят параллельно A1B1C1D1.
- Ортогонально спроецировать все вершины призмы на плоскость П4. Для этого проводят линии связи перпендикулярно оси x14, затем от оси x14 откладывают расстояние до незаменяемой плоскости - координаты z вершин призмы. Координаты z вершин нижнего основания A, D и K равны нулю, следовательно, точки A4,D4, и K4 лежат на оси x14. Координаты z вершин верхнего основания равны (A2B2).
- В системе плоскостей П1/П4 грань ABCD занимает положение фронтальной плоскости уровня, следовательно, проецируется на П4 в натуральную величину.
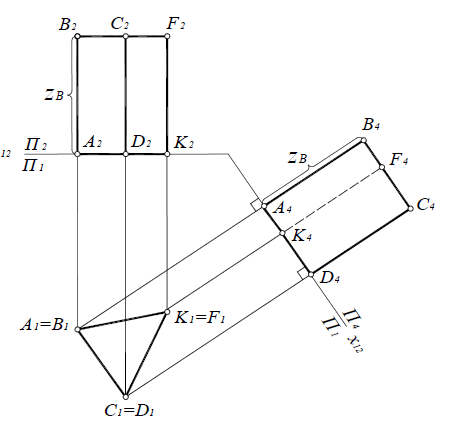
Рис. 11.4. Преобразование грани A BCD в положение плоскости уровня
Способ плоскопараллельного движения
В отличие от способа замены плоскостей проекций, когда данный объект оставался неподвижным, а плоскости проекций изменялись, можно добиться того же результата обратным путем. Оставив плоскости проекций неподвижными, можно перемещать объект в пространстве как неразрывную систему до желаемого положения.
Такое перемещение объекта в пространстве можно выполнить с помощью плоскопараллельного движения.
Плоскопараллельным движением объекта в пространстве называется такое его перемещение, при котором все точки объекта перемещаются в плоскостях, параллельных между собой.
При этом совершенно безразличен вид траектории перемещения точек объекта от исходного до частного положения. Простым примером плоскопараллельного движения является вращение объекта вокруг проецирующей оси. При этом точки описывают окружности в плоскостях, перпендикулярных к оси вращения и, следовательно, параллельных между собой.
При решении задач чаще всего применяют плоскопараллельное движение относительно одной из плоскостей проекций. При этом все точки объекта перемещаются в плоскостях уровня, то есть в плоскостях, параллельных плоскостям проекций. Отсюда следует, что при плоскопараллельном движении относительно плоскости проекций П1 все точки объекта перемещаются в горизонтальных плоскостях уровня, а при плоскопараллельном движении относительно П2- во фронтальных плоскостях уровня (рис. 11.5).
Рис. 11.5. Плоскопараллельное движение точки А относительно горизонтальной плоскости проекций
Теорема. Если объект совершает плоскопараллельное движение относительно плоскости проекций П1, то фронтальные проекции его точек будут двигаться по прямым, перпендикулярным к линиям связи; при этом горизонтальная проекция объекта движется по плоскости проекций, оставаясь равной самой себе.
Применяя плоскопараллельное перемещение относительно плоскости проекций П1 как способ преобразования комплексного чертежа, на основании этой теоремы поступают следующим образом:
- Горизонтальную проекцию данного геометрического объекта вычерчивают без изменения, располагая ее на чертеже так, как требуется для решения задачи.
- Фронтальную проекцию определяют по линиям связи на основании новой горизонтальной проекции.
В случае плоскопараллельного перемещения объекта относительно плоскости проекций П2 горизонтальные проекции точек двигаются по прямым, перпендикулярным к линиям связи, а фронтальная проекция перемещается по плоскости проекций, оставаясь равной самой себе.
Применяя плоскопараллельное перемещение относительно плоскости проекций П2 как способ преобразования комплексного чертежа, поступают следующим образом:
- Фронтальную проекцию данного геометрического объекта вычерчивают без изменения, располагая ее на чертеже желательным образом, так, как требуется для решения задачи.
- Горизонтальную проекцию определяют по линиям связи на основании новой горизонтальной проекции.
Рассмотрим преобразование отрезка [AB] общего положения в положение фронтальной линии уровня, а затем в положение горизонтально-проецирующей прямой способом плоскопараллельного движения (рис. 11.6, 11.7).
Рис. 11.6. Плоскопараллельное движение отрезка AB общего положения
Сначала производится плоскопараллельное движение отрезка [AB] относительно плоскости проекций П1. Для этого новую горизонтальную проекцию отрезка [A1'B1']=[A1B1]нужно разместить так, как требуется для решения задачи, а именно [A1'B1'] (B1B2).
(B1B2).
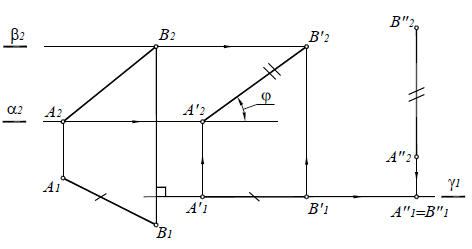
Фронтальные проекции точек A2 и B2 перемещаются по прямым - следам плоскостей движения точек α2 и β2:
а2||β2||П1,
и определяются по линиям связи на основании новой горизонтальной проекции отрезка [A1'B1'].
В результате отрезок [AB] переведен в положение фронтальной линии уровня и определены его натуральная величина [A 2' B 2']=∣AB | и угол наклона φ к горизонтальной плоскости проекций П1.
Далее производится плоскопараллельное движение отрезка AB относительно плоскости проекций П2. В этом случае фронтальная проекция отрезка располагается так, как требуется для решения задачи, а именно:
[A2''B2'']=(A1A2); [A2''B2'']=[A2'B2'].
Горизонтальная проекция перемещается в плоскости γ(γ1), у||П2 и определяется по линиям связи в соответствии с новой фронтальной проекцией [A2''B2'']. Тогда горизонтальной проекцией отрезка будет точка A"1=B"1, а сам отрезок займет горизонтально-проецирующее положение, что и требовалось в данной задаче.
Рассмотрим определение натуральной величины треугольника ABC способом плоскопараллельного движения (рис. 11.8).
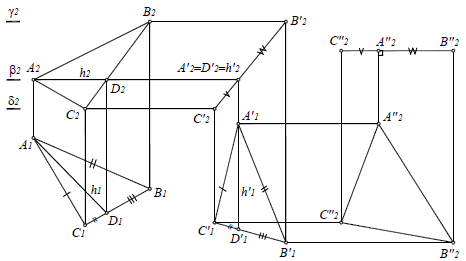
Рис. 11.8. Преобразование плоскости α (ABC) общего положения в плоскость уровня способом плоскопараллельного движения
Данная задача решается в два этапа: сначала плоскость переводится из общего положения в проецирующее, а затем - в положение плоскости уровня.
Сначала производится плоскопараллельное движение плоскости α(ABC) относительно плоскости проекций П1. Для этого в плоскости α(ABC) проводится горизонталь h(h1,h2) и строится новая горизонтальная проекция плоскости α'(A'B'C'), конгруэнтная проекции α(ABC), так, чтобы горизонталь h'(h'1 ,h'2) стала проецирующей прямой, то есть h1'  (A1A2). Тогда фронтальные проекции точек A2, B2, C2 будут перемещаться по прямым - следам плоскостей движения точек δ2, β2 и γ2:
(A1A2). Тогда фронтальные проекции точек A2, B2, C2 будут перемещаться по прямым - следам плоскостей движения точек δ2, β2 и γ2:
δ2∣∣β2∣∣γ2; β2 B1B2;
B1B2;
и определяются по линиям связи на основании новой горизонтальной проекции плоскости α'(A'1B'1C'1). Новая фронтальная проекция плоскости α'2(A'2B'2C'2) представляет собой отрезок прямой.
Вторым плоскопараллельным движением, но уже относительно плоскости проекций П2, плоскость α(ABC) преобразуется в горизонтальную плоскость уровня. Для этого строится новая фронтальная проекция плоскости α''2(A''2B''2C''2) в виде горизонтального отрезка, для которого [C''2A''2] = [C'2A'2] и [A''2B''2] = [A'2B'2]. Новая горизонтальная проекция плоскости α"1(A''1 B''1 C''1) определяется по линиям связи на основании новой фронтальной проекции плоскости α''2(A''2B''2C''2).
Полученная горизонтальная проекция плоскости α''1(A''1B''1C''1) определяет ее натуральную величину: ∆A''1 B''1 C''1= | ∆ ABC |.
Вращение
Вращение - это движение по окружности вокруг некоторой оси. При преобразовании комплексного чертежа способом вращения плоскости проекций остаются неизменными, а проецируемый объект перемещается таким образом, чтобы он занял какое-либо частное положение.
Элементы вращения:
- Ось вращения - прямая, вокруг которой осуществляется вращение.
- Плоскость вращения - плоскость, проходящая через вращаемую точку и перпендикулярная оси вращения (плоскость окружности, которую описывает точка при вращении).
- Центр вращения - точка пересечения оси вращения и плоскости вращения.
- Радиус вращения - кратчайшее расстояние от вращаемой точки до центра (оси) вращения. Радиус всегда перпендикулярен оси вращения.
- Угол поворота - угол между начальным и конечным положением радиуса вращения.
При вращении системы точек вокруг одной оси все точки вращаются в плоскостях, параллельных между собой, поворачиваются на один и тот же угол в одном и том же направлении, поэтому вращение является частным случаем плоскопараллельного перемещения. Точки, находящиеся на оси вращения остаются неподвижными.
Вращение вокруг проецирующей прямой
При вращении точки вокруг оси, перпендикулярной горизонтальной плоскости проекций, ее фронтальная проекция перемещается перпендикулярно линиям связи, а горизонтальная - по окружности, центром которой является горизонтальная проекция оси вращения.
При вращении точки вокруг оси, перпендикулярной фронтальной плоскости проекций, ее горизонтальная проекция перемещается перпендикулярно линиям связи, а фронтальная - по окружности, центром которой является фронтальная проекция оси вращения (рис. 11.9).
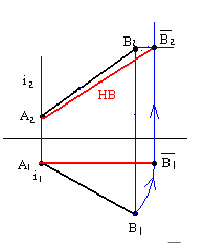
Рассмотрим вращение точки A(A1,A2) вокруг горизонтально- проецирующей прямой i(i1, i1).
При вращении точка описывает окружность, плоскость которой γ(γ2) перпендикулярна оси i(i1, i1). Поскольку i П1 а γ(γ2)
П1 а γ(γ2) i, y(y2)∣∣∏1 и угол поворота φ проецируется на П1 в натуральную величину.
i, y(y2)∣∣∏1 и угол поворота φ проецируется на П1 в натуральную величину.
Таким образом, при вращении вокруг горизонтально-проецирующей прямой i(i1 ,i2 )A1 перемещается по окружности l1 с центром в точке О1 и радиусом r=r1=∣O1A1∣, A2 перемещается по фронтальному следу плоскости γ2 в пределах отрезка [12,22].
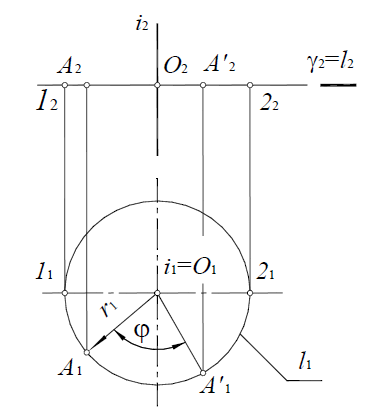
Рис. 11.9. Вращение точки вокруг горизонтально-проецирующей прямой:
i(i1 i2) ∏1 - ось вращения:
∏1 - ось вращения:
γ(γ 2) 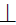 i(i1 i2) - плоскость вращения;
i(i1 i2) - плоскость вращения;
O = γ(γ 2) x i (i1 i 2) — центр вращения;
r = r1 = |O1A1| - радиус вращения;
l - траектория перемещения точки A;
φ - угол поворота точки A
Способом вращения вокруг проецирующей прямой можно совместить точку с плоскостью или поверхностью. Рассмотрим совмещение точки M с поверхностью прямого кругового конуса, поставленного основанием на плоскость П1 (рис. 11.10).
Рис. 11.10. Совмещение точки с поверхностью конуса
Точка M, вращаясь вокруг горизонтально-проецирующей оси i(i1i2) , описывает окружность l , лежащую в горизонтальной плоскости уровня γ(γ2) (рис. 11.11). Точка M должна также принадлежать поверхности конуса, следовательно, необходимо определить линию пересечения n поверхности конуса с плоскостью вращения γ(γ2) .
Затем определяются точки пересечения полученной линии n и окружности l - траектории перемещения точки M . Полученные точки M' и M'' являются точками совмещения точки M с поверхностью конуса.
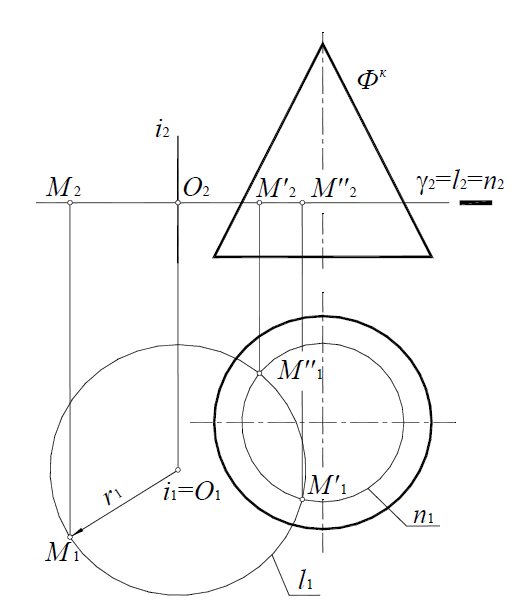
Рис. 11.11. Совмещение точки с поверхностью конуса на комплексном чертеже
Дано: Фк - поверхность конуса,
M(M1M2),
i (i1 i 2)  П1.
П1.
Совместить M(M1M2) с Фк .
Решение:
1. M(M1M2) ∈ γ(γ2) i(i1i2);
i(i1i2);
O2 = γ2 x i2; 01 = i 1; r = ∣O1M∣1; l1 - окружность радиуса r1; 12 = γ2;
2. n = Фк γ(γ2);
γ(γ2);
3. l×n = M`,M'' - точки совмещения M(M1 ,M2) с поверхностью конуса Фк.
Преобразование чертежа
Даже беглый обзор предыдущих глав позволяет придти к выводу, что многие задачи проще решаются, если геометрические объекты занимают частное положение по отношению к плоскостям проекций. Перевести объекты в такое положение можно преобразованием чертежа. Все рассматриваемые в курсе Начертательной геометрии способы преобразования чертежа в конечном счете сводятся к последовательной перемене плоскостей проекций. Именно это и определило рассмотрение способа «перемены плоскостей проекции» в этой главе.
Перемена плоскостей проекции
Способ перемены плоскостей проекций заключается в замене одной из плоскостей проекций 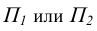 новой плоскостью
новой плоскостью 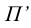 при сохранении ортогональности плоскостей проекции (в соответствии с рисунком 6.1).
при сохранении ортогональности плоскостей проекции (в соответствии с рисунком 6.1).
Изменение положения плоскостей проекции не приводит к изменению формы и положения объектов в пространстве.
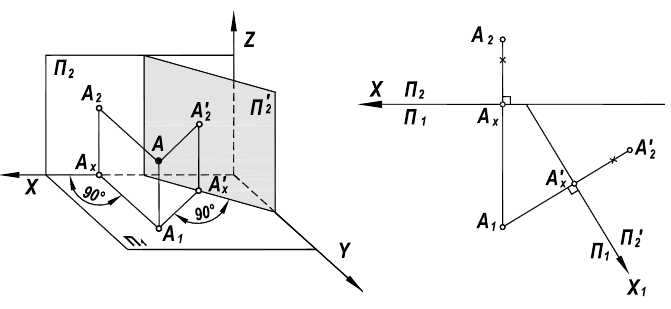
Рисунок 6.1 - Замена фронтальной плоскости проекций
Новая система выбирается так, чтобы получить расположение геометрических объектов наиболее удобное для решения поставленной задачи.
На комплексном чертеже сохраняется перпендикулярность линии связи новой (выбранной при перемене плоскостей проекции) оси чертежа. Сохраняется и расстояние от объекта до оси чертежа на заменяемой плоскости 
В частном случае, когда вновь вводимая плоскость перпендикулярна одновременно плоскостям  получается чертеж, который традиционно интерпретируют как комплексный чертеж с проецированием на три плоскости проекций (рисунок 6.2).
получается чертеж, который традиционно интерпретируют как комплексный чертеж с проецированием на три плоскости проекций (рисунок 6.2).
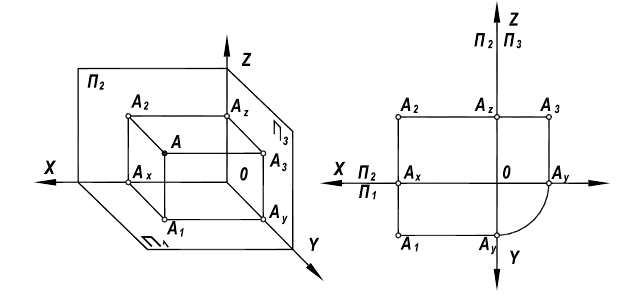
Рисунок 6.2 - Проецирование на три плоскости проекций
Вновь вводимую, в соответствии с рисунком 6.2, плоскость 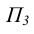 называют профильной, проекцию
называют профильной, проекцию  - профильной проекцией точки. Такой чертеж, в силу того, что он является комбинацией двух комплексных чертежей
- профильной проекцией точки. Такой чертеж, в силу того, что он является комбинацией двух комплексных чертежей 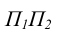 и
и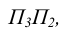 имеет две "самостоятельные оси" чертежа, соответственно Ох и Oz.
имеет две "самостоятельные оси" чертежа, соответственно Ох и Oz.
Преобразование прямой
Отрезок прямой общего положения может быть преобразован в положение прямой уровня и проецирующей прямой.
Преобразование к положению линии уровня можно свести к одной перемене плоскостей проекций. Одно из возможных решений - замена плоскости 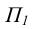 на
на 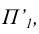 , перпендикулярную к плоскости
, перпендикулярную к плоскости 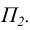 Новая ось чертежа
Новая ось чертежа 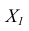 располагается параллельно проекции
располагается параллельно проекции 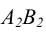 (рисунок 6.3). Расстояние до новой оси чертежа
(рисунок 6.3). Расстояние до новой оси чертежа 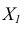 от
от 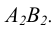 берется произвольно. Новые линии связи перпендикулярны
берется произвольно. Новые линии связи перпендикулярны 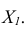 Сохраняются расстояния
Сохраняются расстояния 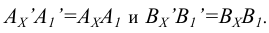 В новой системе линия АВ занимает положение линии уровня.
В новой системе линия АВ занимает положение линии уровня.
Аналогично задача может быть решена и заменой плоскости  (рисунок 6.4).
(рисунок 6.4).
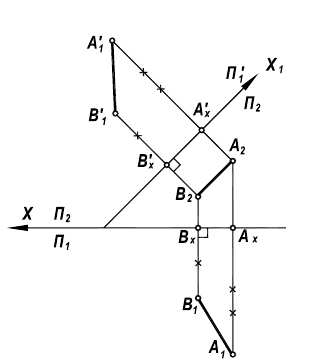
Рисунок 6.3 - Преобразование прямой общего положения в горизонтальную линию уровня
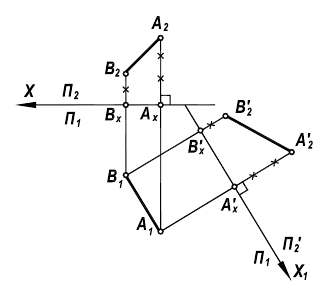
Рисунок 6.4 - Преобразование прямой общего положения во фронтальную линию уровня
Проецирующие прямые в геометрии, иначе, называют еще линиями дважды
уровня. Именно это и определяет последовательность получения положения проецирующей прямой.
На первом этапе решения задачи прямая ЛВ переводится в положение линии уровня (смотри предыдущую задачу).
На втором этапе линия уровня переводится в положение проецирующей прямой. Плоскость 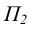 заменяется на
заменяется на 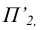 перпендикулярную к плоскости
перпендикулярную к плоскости 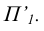 Ось чертежа
Ось чертежа 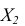 располагается перпендикулярно
располагается перпендикулярно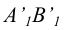 (рисунок 6.5). Расстояние до новой оси чертежа
(рисунок 6.5). Расстояние до новой оси чертежа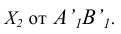 берется произвольно.
берется произвольно.
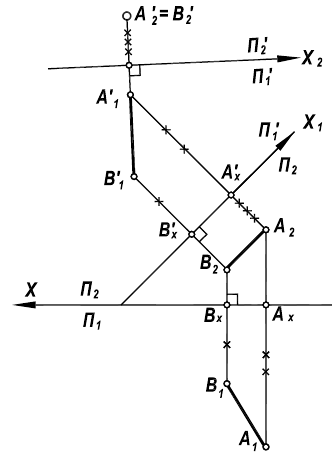
Рисунок 6.5 - Преобразование прямой общего положения во фронтально-проецирующую прямую
Преобразование плоскости
Отсек плоскости общего положения может быть преобразован в положение либо плоскости уровня, либо проецирующей плоскости.
Проецирующая плоскость характеризуется тем, что несет на себе семейство проецирующих линий. В силу параллельности этих прямых достаточно одну из них перевести в положение проецирующей прямой, что автоматически поставит плоскость в положение проецирующей.
На первом этапе решения в плоскости выделяется прямая, например фронталь f (в соответствии с рисунком 6.6). Затем плоскость  заменяется на плоскость на
заменяется на плоскость на  перпендикулярную
перпендикулярную 
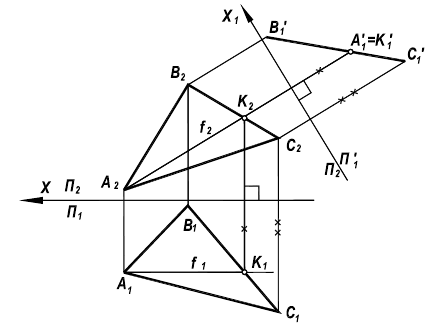
Рисунок 6.6 - Преобразование плоскости общего положения в горизонтально-проецирующую плоскость
В новой системе проецирующих плоскостей  отсек плоскости
отсек плоскости  занимает положение проецирующей плоскости.
занимает положение проецирующей плоскости.
Плоскости уровня, с точки зрения аналитической геометрии, называют еще дважды проецирующими плоскостями.
Преобразование отсека плоскости общего положения к положению плоскости уровня выполняется в два этапа. На первом этапе плоскость переводится в положение проецирующей. На втором этапе (в соответствии с рисунком 6.7) плоскость переводится в положение плоскости уровня заменой плоскости 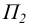 на плоскость на
на плоскость на 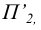 перпендикулярную
перпендикулярную 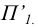
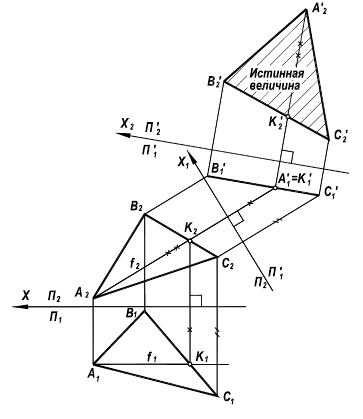
Рисунок 6.7 - Истинная величина треугольника (см. также рисунок 11.22)
В новой системе проецирующих плоскостей  отсек плоскости
отсек плоскости  занимает положение плоскости уровня. Преобразование отрезков прямых и отсеков плоскостей к положению уровня позволяет эффективно решать задачи по нахождению длин отрезков и площадей фигур. Истинная величина объекта, лежащего в плоскости, если плоскость задана следами, может быть определена и вращением этой плоскости вокруг одного из следов.
занимает положение плоскости уровня. Преобразование отрезков прямых и отсеков плоскостей к положению уровня позволяет эффективно решать задачи по нахождению длин отрезков и площадей фигур. Истинная величина объекта, лежащего в плоскости, если плоскость задана следами, может быть определена и вращением этой плоскости вокруг одного из следов.
Вращение вокруг следа плоскости
Способ совмещения - частный случай способа вращения, когда плоскость вращается вокруг одного из ее следов до полного совпадения (совмещения) с плоскостью проекций, в которой лежит этот след.
Отрезки линий и фигуры, лежащие в плоскости, изобразятся на соответствующей плоскости проекций без искажения.
Плоскость общего положения Р может быть совмещена с главной картинной плоскостью П путем вращения около одного из своих следов.
Основой для построения нового изображения служат следующие предпосылки: все точки плоскости перемещаются по окружностям, перпендикулярным оси вращения (соответствующему следу), длины отрезков, лежащих на перемещаемом следе, не изменяются после совмещения плоскостей Р и 
Новое положение вращаемого следа определится из условия того, что сохраняется точка пересечения следов Рх и след проходит через фиксированную точку N (в соответствии с рисунком 6.8 ).
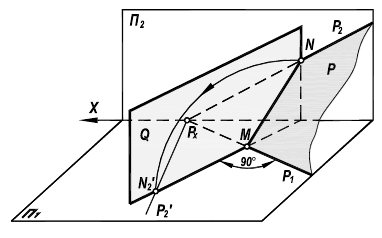
Рисунок 6.8 - Наглядное изо-ражение вращения плоскости вокруг горизонтального следа
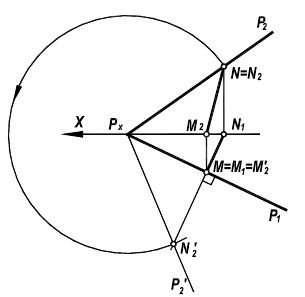
Рисунок 6.9 - Совмещение плоскости с горизонтальной плоскостью проекций
Совмещенное положение точки 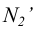 определяется из условия сохранения величин отрезков на вращаемом следе
определяется из условия сохранения величин отрезков на вращаемом следе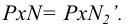 Применительно к комплексному чертежу (рисунок 6.9) при вращении плоскости общего положения Р вокруг горизонтального следа
Применительно к комплексному чертежу (рисунок 6.9) при вращении плоскости общего положения Р вокруг горизонтального следа 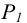 все это выглядит следующим образом.
все это выглядит следующим образом.
На фронтальном следе 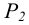 фиксируется произвольная точка N. Ее горизонтальная проекция
фиксируется произвольная точка N. Ее горизонтальная проекция 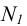 при вращении плоскости не изменит своего положения.
при вращении плоскости не изменит своего положения.
Полагая, что ось преобразованного чертежа совпадет со следом 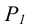 новая фронтальная проекция этой точки
новая фронтальная проекция этой точки 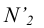 найдется на линии связи перпендикулярной
найдется на линии связи перпендикулярной 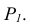 При этом выполняется условие
При этом выполняется условие 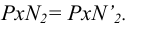
Применение преобразования плоскости
О задачах, связанных с определением взаимного расположения геометрических объектов относительно друг друга, измерением длины отрезка и величины плоской фигуры, говорилось выше, в процессе рассмотрения аппарата преобразования чертежа. Рассмотрим еще несколько других задач.
Расстояние от точки до плоскости
Задача комплексная и предусматривает следующее: проведение из внешней точки к плоскости перпендикулярной прямой, фиксирование точки пересечения этого перпендикуляра с плоскостью и затем определение его длины. Использование перемены плоскостей проекции позволяет упростить процесс решения (рисунок 6.10 ).
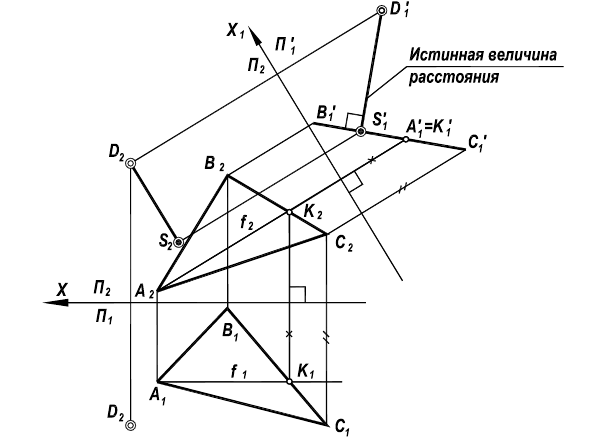
Рисунок 6.10 - Расстояние от точки D до плоскости 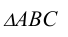
Проведение фронтали а и введение новой оси чертежа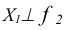 позволяет преобразовать плоскость
позволяет преобразовать плоскость 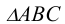 в положение проецирующей (смотри рисунок 6.6). В новой системе плоскостей проекции
в положение проецирующей (смотри рисунок 6.6). В новой системе плоскостей проекции 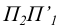 расстояние от точки D до плоскости
расстояние от точки D до плоскости определится длиной отрезка
определится длиной отрезка 
Пересечение прямой и плоскости
Аналогичным же образом решается здесь и вопрос о пересечении прямой общего положения АВ и плоскости Р.
Для определенности положим, что плоскость Р - общего положения (рисунок 6.11).
Фиксирование на фронтальном следе  произвольной точки N и введение новой оси чертежа
произвольной точки N и введение новой оси чертежа перпендикулярной следу
перпендикулярной следу  позволяет построить новое положение следа
позволяет построить новое положение следа  заменив плоскость проекции
заменив плоскость проекции Плоскость Р становится проецирующей.
Плоскость Р становится проецирующей.
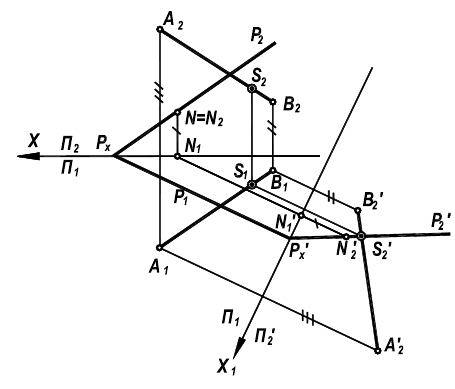
Рисунок 6.11 - Пересечение прямой АВ и плоскости Р
Пересечение следа 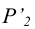 с проекцией
с проекцией 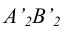 позволяют получить проекцию
позволяют получить проекцию 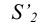 - точки пересечения прямой АВ с плоскостью Р. Проекции точки пересечения
- точки пересечения прямой АВ с плоскостью Р. Проекции точки пересечения 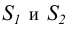 найдутся соответственно по принадлежности этой точки прямой АВ.
найдутся соответственно по принадлежности этой точки прямой АВ.
Методы преобразование чертежа
Задание прямых линий и плоскостей в частных положениях относительно плоскостей проекций значительно упрощает построения и решение различных задач. Существует несколько способов преобразования чертежа, которые позволяют переходить от общих положений геометрических элементов в условиях задач к частным положениям. Рассмотрим эти способы.
Способ замены (перемены) плоскостей проекций
Способ замены плоскостей проекций дает возможность изменить общие положения прямых и плоскостей относительно плоскостей проекций H или V на частные положения введением дополнительных плоскостей проекций.
Сущность способа:
- – положение предмета в пространстве не меняется, а изменяется положение плоскостей проекций относительно этого предмета так, чтобы в дополнительной системе плоскостей проекций предмет занял частное положение (проецирующее или положение уровня), удобное для решения задачи;
- – проецирование предмета на дополнительные плоскости проекций выполняется по методу Г. Монжа – методу параллельного прямоугольного проецирования на взаимно перпендикулярные плоскости, то есть сохраняется взаимная перпендикулярность основных и дополнительных плоскостей проекций.
На рис. 6.1 изображена наглядная картина построения фронтальной проекции отрезка АВ(A"1B"1) на дополнительную плоскость проекций V1.
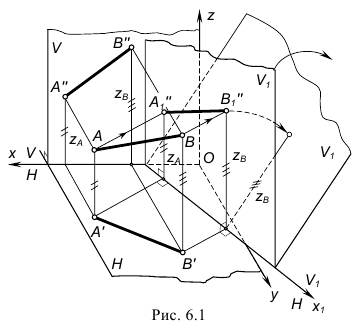
Образована дополнительная система перпендикулярных плоскостей проекций H/V1 c новой осью проекций x1. Обратите внимание, что координаты z фронтальных проекций A"1 и B"1 конечных точек отрезка на дополнительной плоскости V1 равны координатам z фронтальных проекций А" и В" точек в заданной системе x-V/H. Для получения чертежа дополнительную плоскость V1 поворачивают вокруг новой оси проекций x1 до совмещения с плоскостью проекций H.
На рис. 6.2 показан чертеж (эпюр) произвольного преобразования отрезка АВ общего положения двумя последовательными заменами плоскостей проекций, для чего выполнены следующие графические действия:
I замена.
1-е действие. Введена первая дополнительная система x1-H/V1(V1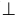 H), ось проекций x1 которой расположена произвольно на поле чертежа.
H), ось проекций x1 которой расположена произвольно на поле чертежа.
2-е действие. Построена в дополнительной плоскости проекций V1 фронтальная проекция A"1B"1 отрезка АВ:
- – проведены линии связи от горизонтальных A' и B' проекций конечных точек отрезка, перпендикулярные оси проекций Х1;
- – от оси проекций x1 отложены координаты z, равные координатам z фронтальных A" и B" проекций точек А и В в заданной системе x-V/H.
II замена.
3-е действие. Введена вторая дополнительная система x2-V1/H1 (H1 V1 ), ось проекций x2 которой расположена произвольно на поле чертежа.
V1 ), ось проекций x2 которой расположена произвольно на поле чертежа.
4-е действие. Построена в дополнительной плоскости проекций H1 горизонтальная проекция A'1 B'1 отрезка АВ:
- – проведены линии связи от построенных в первой дополнительной системе фронтальных проекций точек A"1 и B"1, перпендикулярные оси проекций x2;
- – от оси проекций x2 отложены координаты y, взятые из предыдущей системы x1-H/V1: от оси x1 до горизонтальных A' и B' проекций точек А и В.
Поскольку на рис. 6.2 рассмотрен пример произвольного, без всяких условий, двойного преобразования прямой общего положения, то и в первой и во второй дополнительных системах этот отрезок преобразовался также в прямую общего положения.
Для преобразования прямой или плоскости общего положения в прямую или плоскость частного положения рассмотрим четыре основные задачи преобразования способом замены плоскостей проекций, применяемые как отдельные графические действия для решения различных задач.
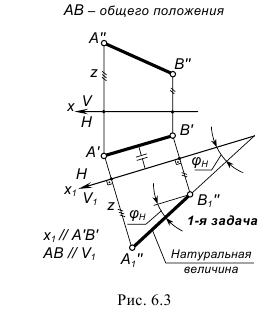
Задача 1. Преобразовать прямую общего положения в прямую уровня.
На рис. 6.3 показано преобразование прямой общего положения АВ во фронтальную прямую уровня. Для решения задачи выполнен следующий графический алгоритм:
1-е действие. Ввести дополнительную систему плоскостей проекций x1-H/V1, расположив ось проекций x1 параллельно горизонтальной проекции A'B' отрезка АВ.
2-е действие. Построить фронтальную проекцию A"1B"1 отрезка в дополнительной плоскости V1 по координатам z, взятым из предыдущей системы x-V/H.
В результате преобразования отрезок AB в дополнительной системе занял положение, параллельное дополнительной плоскости проекций V1, т. е. преобразовался во фронтальную прямую уровня. Следовательно, построены также натуральная величина отрезка и угол его наклона φH к плоскости проекций H.
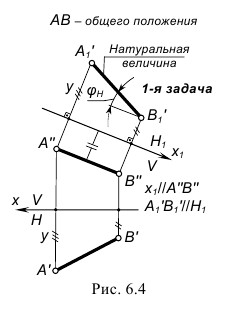
На рис. 6.4 показано преобразование прямой общего положения AB в горизонтальную прямую уровня. Для решения задачи введена дополнительная система плоскостей проекций x1-V/H1 (x1// A"B") и выполнены аналогичные графические действия.
Задача 2. Преобразовать прямую уровня в проецирующую прямую.
На рис. 6.5 показано преобразование фронтальной прямой CD в горизонтально-проецирующую прямую. Для решения задачи выполнен следующий графический алгоритм:
1-е действие. Ввести дополнительную систему плоскостей проекций x1-V/H1, расположив ось проекций x1 перпендикулярно фронтальной проекции C"D" отрезка CD.
2-е действие. Построить горизонтальные совпадающие проекции C'1 и D'1 точек C и D отрезка в дополнительной плоскости проекций H1 по координатам y, взятым из предыдущей системы x-V/H.
В результате преобразования горизонтальный отрезок CD в дополнительной системе занял положение, перпендикулярное дополнительной плоскости проекций H1, т. е. преобразовался в горизонтально-проецирующую прямую.
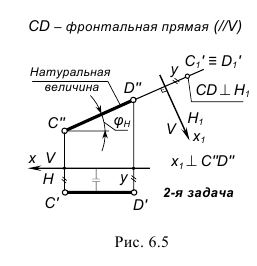
На рис. 6.6 показано преобразование горизонтальной прямой уровня CD во фронтально-проецирующую прямую. Для решения задачи введена дополнительная система плоскостей проекций x1-H/V1 (x1 C'D') и выполнены аналогичные графические действия.
C'D') и выполнены аналогичные графические действия.
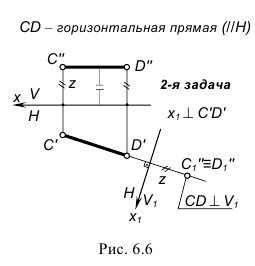
Задача 3. Преобразование плоскости общего положения в проецирующую плоскость.
Чтобы понять сущность графических действий этого преобразования, напомним, что у проецирующих плоскостей, перпендикулярных V или Н, одна из линий уровня – или фронталь, или горизонталь – является проецирующей прямой.
На рис. 6.7 показано, что у горизонтально-проецирующей плоскости α(ABC), горизонтальная проекция которой вырождается в линию, фронталь плоскости f(f",f') занимает положение горизонтально-проецирующей прямой, то есть она перпендикулярна плоскости проекций Н (горизонтальная проекция f (f') вырождается в точку).
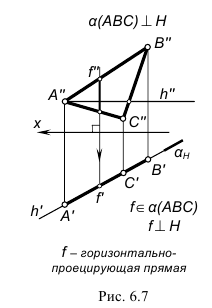
На рис. 6.8 показано, что у фронтально-проецирующей плоскости β(CDE), фронтальная проекция которой вырождается в линию, горизонталь плоскости h(h",h') занимает положение фронтально-проецирующей прямой, то есть она перпендикулярна фронтальной плоскости проекций V (ее фронтальная проекция h(h") вырождается в точку).
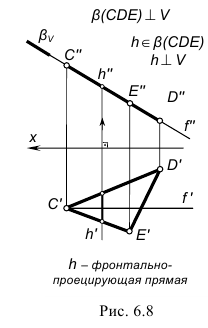
На рис. 6.9 показано преобразование плоскости общего положения во фронтально-проецирующую плоскость. Для решения задачи выполнен следующий графический алгоритм:
1-е действие. Провести в плоскости α(ABC) проекции горизонтали h(h",h').
2-е действие. Ввести дополнительную систему плоскостей x1-H/V1, расположив ось проекций x1 перпендикулярно горизонтальной проекции h' горизонтали плоскости.
3-е действие. Построить в дополнительной плоскости проекций V1 фронтальную проекцию A1"B1"C1" плоскости ABC по координатам z, взятым из предыдущей системы x-V/H, (проекция плоскости выродилась в прямую).
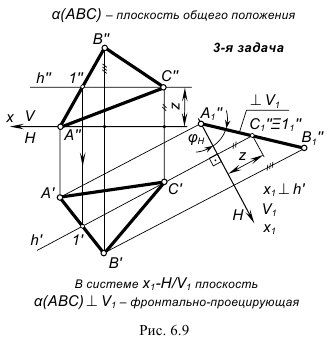
В результате преобразования плоскость общего положения α(ABC) в дополнительной системе заняла положение, перпендикулярное дополнительной плоскости проекций V1, т. е. преобразовалась во фронтально-проецирующую. Следовательно, построен также угол наклона φH плоскости ABC к плоскости проекций H.
На рис. 6.10 показано преобразование плоскости общего положения α(ABC) в горизонтально-проецирующую плоскость. Для решения задачи в плоскости проведены проекции фронтали f(f",f'). Введена дополнительная система плоскостей x1-V/H1, ось x1 которой перпендикулярна фронтальной проекции f" фронтали плоскости, и выполнены аналогичные графические действия.
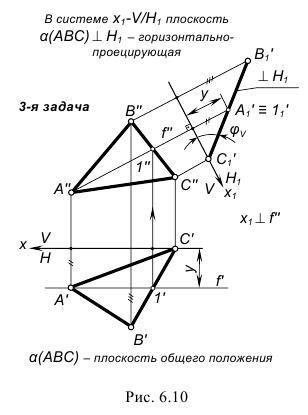
Задача 4. Преобразовать проецирующую плоскость в плоскость уровня.
На рис. 6.11 показано преобразование фронтально-проецирующей плоскости β(CDE) в горизонтальную плоскость уровня. Для решения задачи выполнен следующий графический алгоритм.
1-е действие. Ввести дополнительную систему плоскостей проекций x1-V/H1, расположив ось проекций x1 параллельно вырожденной фронтальной проекции C"D"E" плоскости CDE.
2-е действие. Построить горизонтальную проекцию C'1D'1E'1 в дополнительной плоскости H1 по координатам y, взятым из предыдущей системы x-V/H.
В результате преобразования фронтально-проецирующая плоскость β(CDE) в дополнительной системе заняла положение, параллельное дополнительной плоскости проекций H1, т. е. преобразовалась в горизонтальную плоскостью уровня. Следовательно, построена натуральная величина этой плоскости.
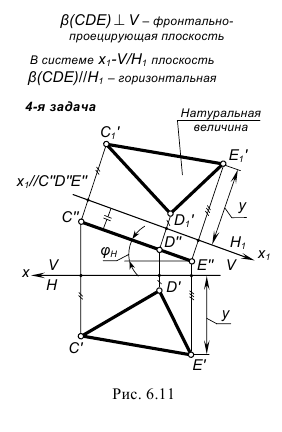
На рис. 6.12 показано преобразование горизонтально-проецирующей плоскости β(CDE) во фронтальную плоскость уровня. Для решения задачи введена дополнительная система x1-H/V1 и выполнены аналогичные графические действия.
Способ вращения вокруг проецирующей оси (фронтально-проецирующей или горизонтально-проецирующей прямой).
Сущность способа в том, что предмет, занимающий общее положение относительно плоскостей проекций, вращают вокруг проецирующей оси, изменяя его положение в пространстве так, чтобы предмет занял частное положение относительно тех же плоскостей проекций, т. е. стал перпендикулярным (проецирующим) либо параллельным (уровня) плоскости проекций H или V.
На рис. 6.13 показана наглядная картина способа на примере вращения точки B вокруг фронтально-проецирующей оси i.
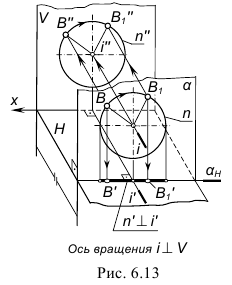
Точка B перемещается в положение B1, вращаясь по окружности n вокруг фронтально-проецирующей оси i в некоторой плоскости α, перпендикулярной плоскости проекций H.
На плоскость проекций Н эта окружность проецируется в прямую линию n(n'), перпендикулярную оси вращения i(i').
На плоскость проекций V окружность n вращения точки B проецируется в окружность n" с центром в точке i(i"), которая является вырожденной проекцией фронтально-проецирующей оси вращения i.
На рис. 6.14 и 6.15 показаны примеры применения способа вращения вокруг проецирующей оси для построения натуральной величины отрезка AB общего положения.
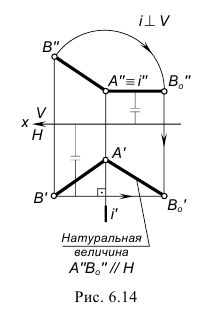
На чертеже натуральную величину имеют прямые уровня, параллельные плоскости проекций H или V (профильную прямую не рассматриваем).
Характерный признак прямых уровня на чертеже – одна из проекций параллельна оси проекций x: горизонтальная проекция для фронтальной прямой и фронтальная проекция – для горизонтальной прямой.
Следовательно, для решения задачи отрезок AB общего положения нужно повернуть (вращать) вокруг проецирующей оси так, чтобы он занял положение, параллельное плоскости проекций H или V.
Для решения задачи выполнен следующий графический алгоритм:
1-е действие. Выбрать ось вращения i, проходящую через любую конечную точку отрезка (на рис. 6.14 фронтально-проецирующая ось вращения проведена через точку А(A",A')), и обозначить ее проекции i(i",i') на чертеже.
2-е действие. Повернуть фронтальную проекцию точки B(В") вокруг оси i(i") по часовой стрелке (можно против) так, чтобы фронтальная проекция отрезка AB(A"B") заняла горизонтальное положение A"Bо", параллельное оси проекций x.
3-е действие. Построить натуральную проекцию A'Bо' отрезка АВ, переместив горизонтальную проекцию точки В перпендикулярно горизонтальной проекции оси вращения i(i') (параллельно оси проекций x) до пересечения с вертикальной линией связи от точки Bо".
В результате преобразования отрезок АВ занял положение горизонтальной прямой уровня.
!!! Конечная точка отрезка A при вращении остается неподвижной, так как лежит на оси вращения i.
На рис. 6.15 показано построение натуральной величины отрезка общего положения AB вращением вокруг горизонтально-проецирующей оси аналогичными графическими действиями (отрезок АВ занял положение фронтальной прямой уровня).
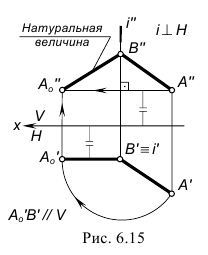
Плоскопараллельное перемещение
Частный случай способа вращения вокруг проецирующей оси – вращение предмета без указания на чертеже осей вращения, который называют способом плоскопараллельного перемещения. Способ удобен тем, что повернутые вокруг предполагаемой проецирующей оси проекции предмета перемещают и располагают на свободном поле чертежа без взаимного их наложения.
На рис. 6.16 показано построение натуральной величины плоскости общего положения, заданной треугольником ABC, способом плоскопараллельного перемещения.
Для решения задачи плоскость АВС должна занять положение плоскости уровня
- – или фронтальной (//V) или горизонтальной (//H). Следовательно, плоскость нужно вращать и одновременно перемещать пополю чертежа, чтобы она последовательно заняла сначала проецирующее положение, а затем положение плоскости уровня.
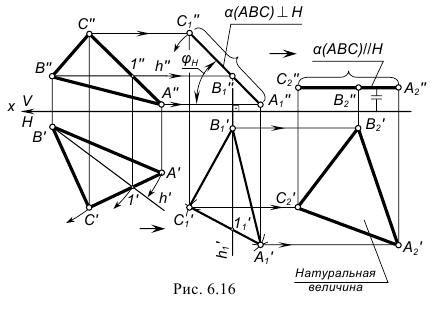
Для двух последовательных преобразований нужно выполнить следующий графический алгоритм.
Первое перемещение. Плоскость общего положения α(АВС) вращением вокруг предполагаемой, например, горизонтально-проецирующей оси преобразовать во фронтально-проецирующую плоскость, выполнив следующие графические действия:
1-е действие. Провести в плоскости горизонталь h(h',h").
2-е действие. Повернуть горизонтальную проекцию A'B'C' треугольника, вращая вокруг предполагаемой горизонтально-проецирующей оси (например, проходящей через точку B') и одновременно перемещая вправо на свободное поле чертежа так, чтобы горизонталь h плоскости заняла положение фронтально-проецирующей прямой, то есть h1' должна расположиться перпендикулярно оси x. Повернутую проекцию треугольника A1'B1'C1' относительно проекции горизонтали h1' построить с помощью дуговых засечек, на пересечении которых определяются вершины.
3-е действие. Построить фронтальную проекцию A1"B1"C1" треугольника, переместив заданные фронтальные A"B"C" проекции вершин треугольника параллельно оси проекций x до пересечения с вертикальными линиями связи от точек A1', B1' и C1' повернутой проекции: фронтальная проекция выродилась в линию, то есть треугольник преобразовался во фронтально-проецирующую плоскость.
Второе перемещение. Плоскость фронтально-проецирующую вращением вокруг предполагаемой фронтально-проецирующей оси преобразовать в горизонтальную плоскость уровня, продолжая графические действия:
4-е действие. Повернуть построенную вырожденную проекцию A1"B1"C1" треугольника, вращая вокруг предполагаемой фронтально-проецирующей оси, проходящей через точку A1", и одновременно перемещая вправо на свободное поле чертежа так, чтобы эта проекция расположилась параллельно оси проекций x: проекция A2"B2"C2" // оси x.
5-е действие. Построить новую горизонтальную проекцию A2'B2'C2' треугольника, переместив горизонтальные проекции A1', B1' и C1' вершин треугольника параллельно оси проекций x до пересечения вертикальными линиями связи от фронтальных проекций A2", B2" и C2" вершин; построенная горизонтальная проекция A2'B2'C2' треугольника и есть его натуральная величина, так как после второго перемещения треугольник преобразовался в горизонтальную плоскость уровня.
Способ вращения вокруг прямой уровня – горизонтальной или фронтальной прямой.
Сущность способа в том, что плоскость общего положения изменяет свое положение в пространстве относительно плоскостей проекций вращением вокруг линии уровня до положения, параллельного плоскости проекций V (или H).
На рис. 6.17 показана наглядная картина вращения плоскости общего положения α(АВС) вокруг горизонтальной прямой. Пусть сторона AB треугольника АВС лежит в плоскости γ, параллельной плоскости проекций H, и является горизонтальной прямой h, вокруг которой и будет повернута плоскость ABC.
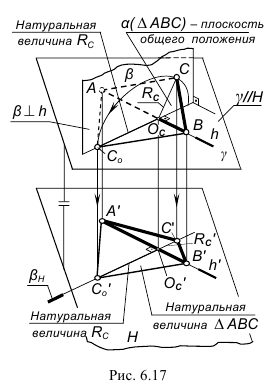
Поскольку вершины A и B треугольника лежат на оси вращения h и, следовательно, неподвижны, то требуется повернуть вокруг прямой уровня h только вершину C так, чтобы она совместилась с плоскостью γ. Вершина C вращается вокруг горизонтальной прямой h (стороны АВ) в плоскости β, перпендикулярной оси вращения h.
После поворота треугольник ABCо лежит в плоскости γ и, следовательно, параллелен плоскости H. Точка C имеет радиус вращения Rc и на плоскость γ этот радиус проецируется в натуральную величину.
Рассмотрим проекцию этой картины на плоскость проекций H. На горизонтальной проекции видно, что натуральную величину A'B'C'о треугольника ABC определяет натуральная величина радиуса вращения Rc точки C.
На рис. 6.18 показано построение на чертеже натуральной величины плоскости α(АВС) способом вращения вокруг горизонтальной прямой уровня h. В этом случае выполняется вращение горизонтальной проекции A'B'C' треугольника, то есть вращение выполняется относительно плоскости проекций, которой параллельна ось вращения.
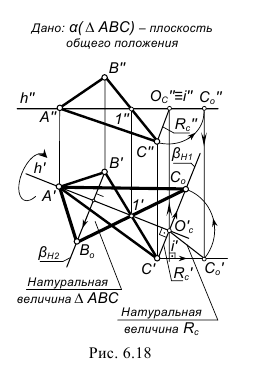
Для решения задачи выполнен следующий графический алгоритм:
1-е действие. В заданной плоскости ABC провести проекции горизонтали h(h",h'), которая является осью вращения.
2-е действие. Провести следы плоскостей βH1 и βH2 перпендикулярно h', в которых будут вращаться вершины B(B') и C(C') вокруг оси вращения h'; точка A(A') будет неподвижна, так как лежит на оси вращения.
3-е действие. Определить проекции отрезка COc(C'Oc',C"Oc"), то есть радиуса Rc вращения точки C вокруг горизонтали h(h') и построить любым рассмотренным графическим способом натуральную величину радиуса вращения Rc(R"c,Rc'); в примере натуральная величина Rc построена способом вращения отрезка общего положения OCc вокруг фронтально-проецирующей оси, вырожденная проекция которой совпадает с проекцией точки Oc(Oc") (по аналогии с построениями на рис. 6.14).
4-е действие. Построенную натуральную величину радиуса вращения Rc=Oc'Co' повернуть и расположить на следе плоскости βH1, в которой вращается точка С(C') треугольника, построив вершину Co в повернутом положении.
5-е действие. Достроить повернутую проекцию треугольника A'BoBo, определив повернутую проекцию Bo вершины B(B') на пересечении следа плоскости вращения βH2 с прямой, проходящей через точки Co и 1(1'), то есть натуральную величину радиуса вращения для точки B определять нет необходимости – ее повернутое положение Bo определяется графическим построением.
В результате преобразования проекция A'BoCo треугольника заняла положение, параллельное горизонтальной плоскости проекций H и, следовательно, определяет его натуральную величину.
!!! Построение на чертеже натуральной величины плоскости ABC вращением вокруг фронтальной прямой уровня f(f",f') выполняется аналогичными графическими действиями, только вращать следует фронтальную проекцию A"B"C" треугольника, так как ось вращения f параллельна фронтальной плоскости проекций. Треугольник после вращения занимает положение фронтальной плоскости уровня, которая определяет его натуральную величину (рис. 6.19).
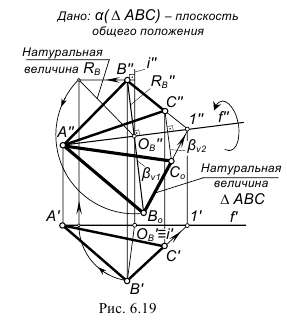
Структуризация материала шестой лекции в рассмотренном объеме схематически представлена на рис. 6.20 (лист 1). На последующих листах 2 и 3 компактно приведены иллюстрации к этой схеме для визуального закрепления изученного материала при повторении (рис. 6.21 и 6.22).
Преобразование
Сущность преобразования чертежа: изменить графическое условие задачи таким образом, чтобы объект преобразования занял относительно плоскости проекций частное положение (проецирующее или положение уровня), которое упрощает графическое решение задачи.
Замена плоскостей проекций
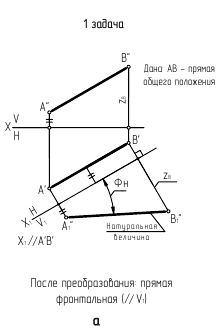
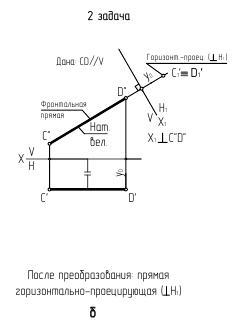
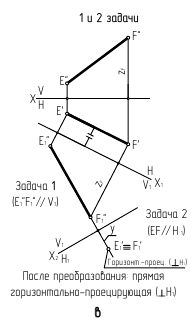
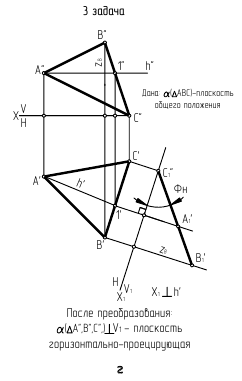
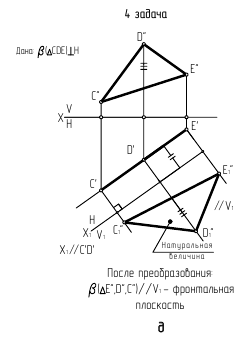
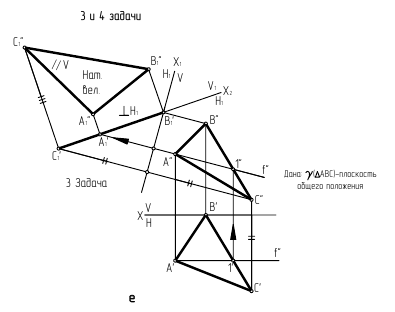
Вращение вокруг проецирующей прямой
1 задача
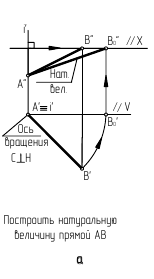
2 задача
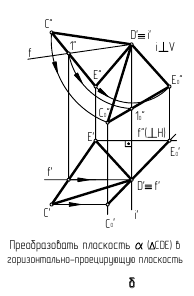
3 задача
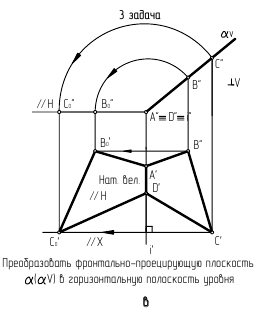
Плоскопараллельное перемещение
1 перемещение 2 перемещение
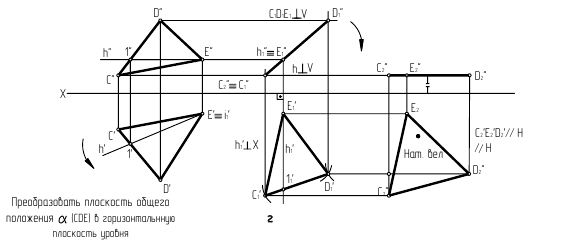
Вращение вокруг линии уровня
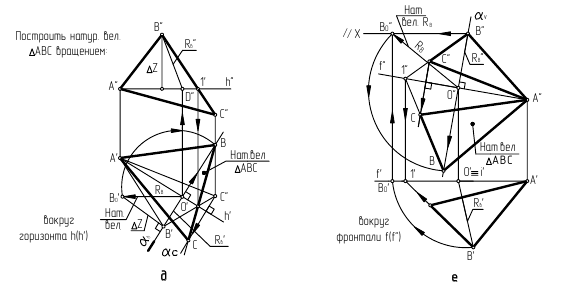
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |