
Предельные теоремы теории вероятностей - определение и вычисление с примерами решения
Содержание:
Предельные теоремы теории вероятностей:
Как уже говорилось при изучении случайных величин, невозможно заранее предсказать, какое значение примет случайная величина в результате единичного испытания – это зависит от многих причин, учесть которые невозможно. Однако при многократном повторении испытаний характер поведения суммы случайных величин почти утрачивает случайный характер и становится закономерным. Наличие закономерностей связано именно с массовостью явлений, порождающих в своей совокупности случайную величину, подчиненную вполне определенному закону. Суть устойчивости массовых явлений сводится к следующему: конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате массы таких явлений; случайные отклонения от среднего, неизбежные в каждом отдельном явлении, в массе взаимно погашаются, нивелируются, выравниваются. Именно эта устойчивость средних и представляет собой физическое содержание «закона больших чисел», понимаемого в широком смысле слова: при очень большом числе случайных явлений их результат практически перестает быть случайным и может быть предсказан с большой степенью определенности.
В узком смысле слова под «законом больших чисел» в теории вероятностей понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа опытов к некоторым определенным постоянным. Закон больших чисел играет важную роль в практических применениях теории вероятностей. Свойство случайных величин при определенных условиях вести себя практически как не случайные позволяет уверенно оперировать этими величинами, предсказывать результаты массовых случайных явлений почти с полной определенностью.
Возможности таких предсказаний в области массовых случайных явлений еще больше расширяются наличием другой группы предельных теорем, касающихся уже не предельных значений случайных величин, а предельных законов распределения. Речь идет о группе теорем, известных под названием «центральной предельной теоремы». Различные формы центральной предельной теоремы различаются между собой теми условиями, для которых устанавливается это предельное свойство суммы случайных величин. Различные формы закона больших чисел с различными формами центральной предельной теоремы образуют совокупность так называемых предельных теорем теории вероятностей. Предельные теоремы дают возможность не только осуществлять научные прогнозы в области случайных явлений, но и оценивать точность этих прогнозов.
Неравенство Чебышёва
Для любой случайной величины Х, имеющей математическое ожидание и дисперсию, справедливо неравенство Чебышёва: 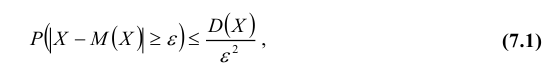
В этой форме неравенство устанавливает верхнюю границу вероятности
рассматриваемого события. Учитывая, что события 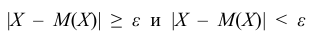 противоположны, неравенство Чебышёва можно записать и в другой форме:
противоположны, неравенство Чебышёва можно записать и в другой форме: 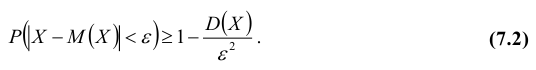 В этой форме оно устанавливает нижнюю границу вероятности рассматриваемого события.
В этой форме оно устанавливает нижнюю границу вероятности рассматриваемого события.
Пример:
Оценить вероятность того, что отклонение любой случайной величины от ее математического ожидания по абсолютной величине будет не более трех средних квадратических отклонений (правило трех сигм).
Решение:
Учитывая, что 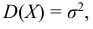 получаем:
получаем:
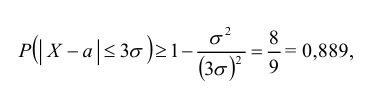 т.е. не менее, чем 0,899. Напомним, что для нормального закона правило трех сигм выполняется с вероятностью Р = 0,9973. Можно показать, что для равномерного закона распределения Р = 1, для показательного – Р = 0,9827 и т.д. Таким образом, правило трех сигм с достаточно большой вероятностью его выполнения, применимо для большинства случайных величин, встречающихся на практике. ◄
т.е. не менее, чем 0,899. Напомним, что для нормального закона правило трех сигм выполняется с вероятностью Р = 0,9973. Можно показать, что для равномерного закона распределения Р = 1, для показательного – Р = 0,9827 и т.д. Таким образом, правило трех сигм с достаточно большой вероятностью его выполнения, применимо для большинства случайных величин, встречающихся на практике. ◄
Теорема Чёбышева
Теорема. Если дисперсия n независимых случайных величин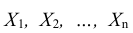 ограничена одной и той же постоянной С, то при неограниченном увеличении числа n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий
ограничена одной и той же постоянной С, то при неограниченном увеличении числа n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий 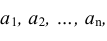 , т.е.
, т.е.
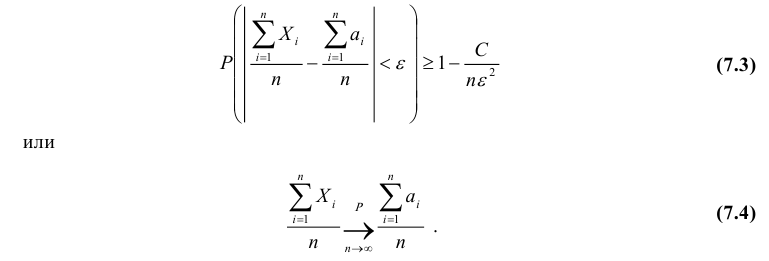
Поясним смысл формулировки «сходимость по вероятности». Понятие предела переменной величины 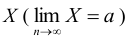 означает, что, начиная с некоторого момента ее изменения для любого (даже сколь угодно малого) числа ε > 0, будет верно неравенство │Х – а│< ε. В круглых скобках выражения (7.3) содержится аналогичное выражение
означает, что, начиная с некоторого момента ее изменения для любого (даже сколь угодно малого) числа ε > 0, будет верно неравенство │Х – а│< ε. В круглых скобках выражения (7.3) содержится аналогичное выражение
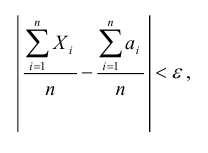
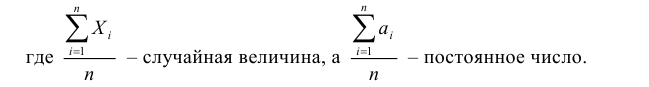
Однако из (7.3) не следует, что это неравенство будет выполняться всегда, начиная с некоторого момента изменения 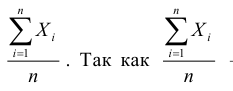 – случайная величина, то возможно, что в о т д е л ь н ы х случаях неравенство выполняться не будет. Однако с увеличением числа n вероятность неравенства
– случайная величина, то возможно, что в о т д е л ь н ы х случаях неравенство выполняться не будет. Однако с увеличением числа n вероятность неравенства 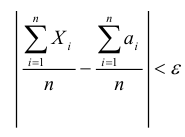 стремится к единице, т.е. это неравенство будет выполняться в подавляющем числе случаев. Другими словами, при достаточно больших n выполнение рассматриваемого неравенства является событием практически достоверным, а неравенство противоположного смысла – практически невозможным. Подчеркнем смысл теоремы Чебышёва. При большом числе случайных величин практически достоверно, что их средняя
стремится к единице, т.е. это неравенство будет выполняться в подавляющем числе случаев. Другими словами, при достаточно больших n выполнение рассматриваемого неравенства является событием практически достоверным, а неравенство противоположного смысла – практически невозможным. Подчеркнем смысл теоремы Чебышёва. При большом числе случайных величин практически достоверно, что их средняя 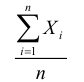 – величина случайная , как угодно мало отличается от неслучайной величины
– величина случайная , как угодно мало отличается от неслучайной величины 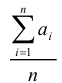 , т.е. практически перестает быть случайной.
, т.е. практически перестает быть случайной.
Следствие. Если независимые случайные величины 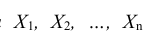 имеют одинаковые математические ожидания, а их дисперсии ограничены одной и той же постоянной, то формулы теоремы Чебышёва принимают вид:
имеют одинаковые математические ожидания, а их дисперсии ограничены одной и той же постоянной, то формулы теоремы Чебышёва принимают вид:
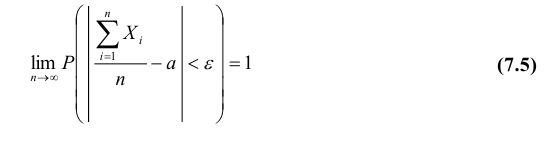 или
или

Теорема Чебышёва и ее следствие имеют большое практическое значение. Например, страховой компании необходимо установить размер страхового взноса, который должен уплачивать страхователь. При этом страховая компания обязуется выплатить при наступлении страхового случая определенную страховую сумму. Рассматривая частоту страховых случаев как величину случайную и обладая статистикой таких случаев, можно определить среднее число страховых случаев, которое на основании теоремы Чебышёва с большой степенью уверенности можно считать величиной почти не случайной. Тогда на основании этих данных и предполагаемой страховой суммы определяется размер страхового взноса.
Пример:
Сколько надо провести измерений случайной величины, чтобы с вероятностью не менее 0,95 гарантировать отклонение средней арифметической этих измерений от истинного значения величины менее, чем на 1 (по абсолютной величине), если среднее квадратическое отклонение каждого из измерений не превосходит 5?
Решение:
Используя теорему Чебышёва, найдем n, при котором
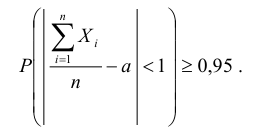
Данное неравенство выполняется, если :
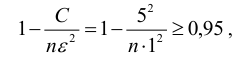
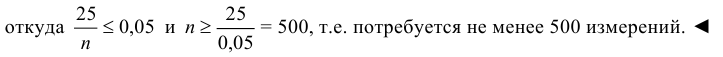
Отметим важные частные случаи теоремы Чебышёва: теоремы Бернулли и Пуассона.
Теорема Бернули
Теорема. Частость события в n повторных независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р, при неограниченном увеличении числа испытаний сходится по вероятности к вероятности этого события в отдельном испытании:
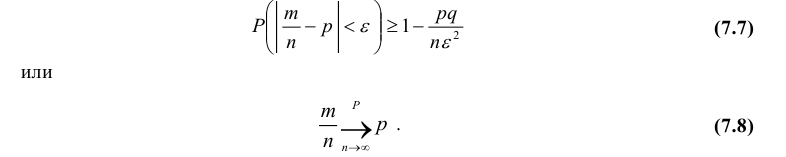
Теорема Бернулли дает теоретическое обоснование замены неизвестной вероятности события его частостью, или статистической вероятностью, полученной в n повторных независимых испытаниях. Непосредственным обобщением теоремы Бернулли является теорема Пуассона, когда вероятности события в каждом испытании различны.
Теорема Пуассона
Теорема. Частость события в n повторных испытаниях, в каждом из которых оно может произойти соответственно с вероятностями 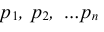 при неограниченном увеличении числа испытаний сходится по вероятности к средней арифметической вероятностей события в отдельном испытании:
при неограниченном увеличении числа испытаний сходится по вероятности к средней арифметической вероятностей события в отдельном испытании:

Закон больших чисел может быть распространен и на зависимые случайные величины. Обобщение закона больших чисел на случай зависимых случайных величин принадлежит А. А. Маркову.
Теорема Маркова
Теорема. Если имеются зависимые случайные величины 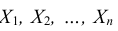 и если при n→ ∞ выполняется условие
и если при n→ ∞ выполняется условие

то среднее арифметическое этих случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий

Центральная предельная теорема
Рассмотренный закон больших чисел устанавливает факт приближения средней большого числа случайных величин копределеным постоянным. Но этим не ограничиваются закономерности, возникающие в результате суммарного действия случайных величин. Оказывается, что при некоторых условиях совокупное действие случайных приводит к определённому , а именно – к нормальному закону распределения.
Центральная предельная теорема представляет собой группу теорем, посвященных установлению условий, при которых возникает нормальный закон распределения. Среди этих теорем важнейшее место принадлежит теореме Ляпунова.
Теорема Ляпунова
Теорема. Если 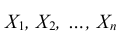 – независимые случайные величины, у каждой из которых существует математическое ожидание
– независимые случайные величины, у каждой из которых существует математическое ожидание 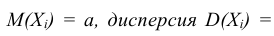
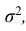 , абсолютный центральный момент третьего порядка
, абсолютный центральный момент третьего порядка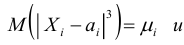 выполняется условие
выполняется условие
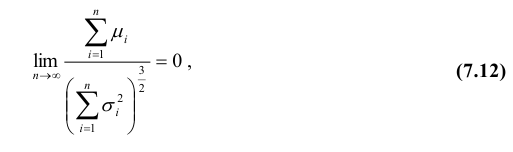
то закон распределения суммы 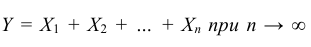 неограниченно приближается к нормальному с математическим ожиданием
неограниченно приближается к нормальному с математическим ожиданием 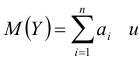 дисперсией
дисперсией 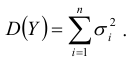 Смысл условия (7.12) состоит в том, чтобы в сумме
Смысл условия (7.12) состоит в том, чтобы в сумме 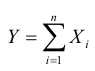 не было слагаемых, влияние которых на рассеяние суммарной величины Y подавляюще велико по сравнению с влиянием остальных. Также не должно быть большого числа случайных слагаемых, влияние которых очень мало по сравнению с суммарным влиянием остальных. Таким образом, удельный вес каждого отдельного слагаемого должен стремиться к нулю при увеличении числа слагаемых.
не было слагаемых, влияние которых на рассеяние суммарной величины Y подавляюще велико по сравнению с влиянием остальных. Также не должно быть большого числа случайных слагаемых, влияние которых очень мало по сравнению с суммарным влиянием остальных. Таким образом, удельный вес каждого отдельного слагаемого должен стремиться к нулю при увеличении числа слагаемых.
Следствие. Если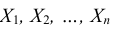 – независимые случайные величины, у которых существуют равные математические ожидания
– независимые случайные величины, у которых существуют равные математические ожидания 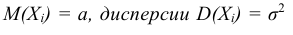 и абсолютные центральные моменты третьего порядка
и абсолютные центральные моменты третьего порядка 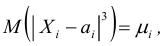 то закон распределения суммы
то закон распределения суммы 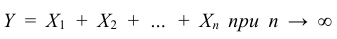 неограниченно приближается к нормальному с математическим ожиданием
неограниченно приближается к нормальному с математическим ожиданием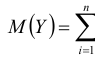 и
и 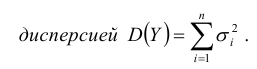 В частности, если все случайные величины распределены одинаково, то закон распределения их суммы неограниченно приближается к нормальному закону при n → ∞.
В частности, если все случайные величины распределены одинаково, то закон распределения их суммы неограниченно приближается к нормальному закону при n → ∞.
Теорема Берри-Эссена
Однако при этом встает вопрос, при каких значениях n можно использовать нормальное приближение, а при каких – нет. Решение этого вопроса зависит от требуемой точности вычисления вероятности. Часто теорему Муавра-Лапласа применяют при выполнении условия npq > 10, а центральную предельную теорему, если np > 10. Точный ответ на вопрос о погрешности, возникающей при замене исходного распределения нормальным, дает оценка скорости сходимости в центральной предельной теореме. Такая оценка приводится в теореме Берри-Эссена.
Теорема. Если 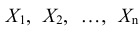 – независимые, одинаково распределенные случайные величины с математическим ожиданием а, дисперсией σ2 и третьим абсолютным центральным моментом μ3, то имеет место неравенство
– независимые, одинаково распределенные случайные величины с математическим ожиданием а, дисперсией σ2 и третьим абсолютным центральным моментом μ3, то имеет место неравенство
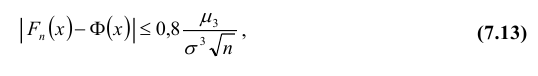
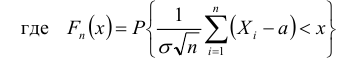 функция распределения нормированной суммы, Ф(х)– функция распределения нормального закона с параметрами а = 0 и σ2 =1.
функция распределения нормированной суммы, Ф(х)– функция распределения нормального закона с параметрами а = 0 и σ2 =1.
Пример:
Оценить с помощью теоремы Берри-Эссена погрешность, возникающую при использовании теоремы Муавра-Лапласа.
Решение:
В тереме Муавра-Лапласа распределение нормированной суммы независимых случайных величин, имеющих распределение Бернулли, заменяется нормальным.

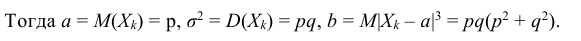
Применяя теорему Берри-Эссена, получаем:
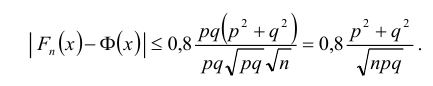
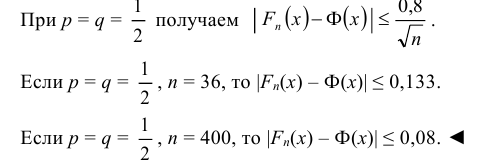
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |