Предел и непрерывность функции двух переменных с примерами решения

Содержание:

Множества точек n-мерного евклидова пространства:

Назовем n-мерным координатным пространством и обозначим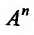

Координатное пространство 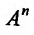называется n-мерным евклидовым пространством и обозначается 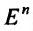, если между двумя любыми точками 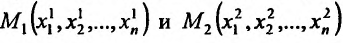пространства 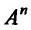определено расстояние, обозначаемое 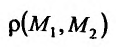и вычисляемое по формуле:

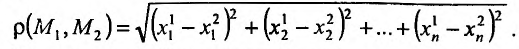
Опишем важнейшие типы множеств n-мерного евклидова пространства .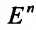

Множество 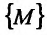всевозможных точек М пространства 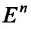, координаты которых удовлетворяют:

• а) неравенству
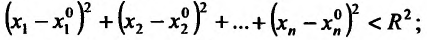
• б) неравенству
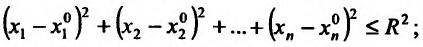
• в) равенству
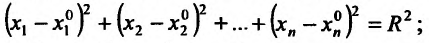
• г) неравенствам

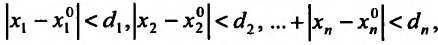
где 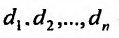- некоторые положительные числа, называется:

• а) открытым n-мерным шаром;
• б) замкнутым n-мерным шаром;
• в) n-мерной сферой радиуса R с центром в точке
• г) открытым n-мерным координатным параллелепипедом с центром в точке

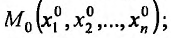
Открытый n-мерный шар раднуса 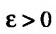с центром в точке 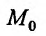будем называть 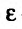-окрестностью точки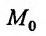

Множество {М} точек пространства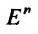 называется ограниченным, если найдется n-мерный шар, содержащий все точки этого множества.

Определение функции n переменных, двух переменных

Определение 15.2.1. Пусть задано множество точек {М} n-мерного евклидова пространства 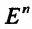. Если каждой точке М из множества {М) ставится в соответствие по известному закону некоторое число и, то говорят, что на множестве {м} задана функция u = u(х) или 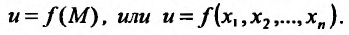. При этом множество {M} называют областью задания функции 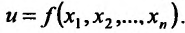. Число u соответствующее данной точке М из множества {M}, называется частным значением функции в точке М. Совокупность {м} всех частных значений функции 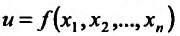называется множеством значений этой функции.

Частным случаем функции n переменных является функция двух переменных, которую можно определить следующим образом.

Если каждой паре (х, у) значений двух независимых друг от друга переменных величин х и у. принадлежащих области D, соответствует по известному закону определенное значение величины z, то 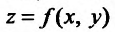называется функцией двух независимых переменных х и у, определенной в области D. D называется областью определения функции z = f(x, у).

Функция двух независимых переменных может быть задана:

• аналитически, то есть с помощью формул;
• при помощи таблицы, в которой указываются частные значения х и y, и соответствующие значения z;
• при помощи компьютерной программы, в которой определен алгоритм получения значений функции z для частных значений х и y

Для определения частных значений функции двух переменных должны быть заданы значения независимых переменных: 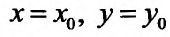И поэтому ясно, что функция z =f(х, у) может быть определена на всей плоскости или в некоторой ее части, то есть в некоторой области. Область определения как всякое множество может быть открытой (незамкнутой) или замкнутой.

Рассмотрим функцию

определенную в области D на плоскости Оху и систему прямоугольных декартовых координат Oxyz. В каждой точке (x, у) восстановим перпендикуляр к плоскости Оху и на ней отложим отрезок, равный f(x,y). Тогда получим точку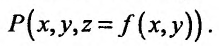

Геометрическое место точек Р, координаты которых удовлетворяют (15.2.1), называется графиком функции двух переменных. Но уравнение (15.2.1) определяет некоторую поверхность, следовательно, графиком функции двух переменных является поверхность, проектирующаяся на плоскость Оху в область определения функции.

Например, областью задания функции двух переменных 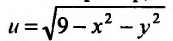является круг радиуса 3 с центром в начале координат, а множество значений представляет собой отрезок.

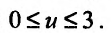Область задания функции n переменных 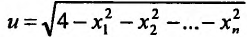служит n-мерный шар радиуса 2 с центром в точке O(0,0.....0). Множеством значений рассматриваемой функции является отрезок [0;2],

Из приведенных примеров, видим, что область задания функции n переменных представляет собой некоторое множество точек n-мерного евклидова пространства 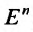, а множество всех значений этой функции- множество одномерного евклидова пространства .

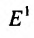Предел функции двух переменных

Определение 15.3.1. (предел функции по Кохии) Число А называется пределом функции z = f(M) в точке 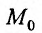(или при 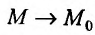). если для любого положительного числа 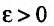найдется такое положительное число 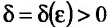, что для любой точки М из множества 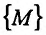задания этой функции, удовлетворяющей условию 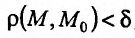, справедливо неравенство .

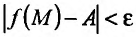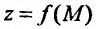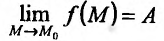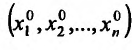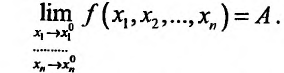Для обозначения предела функции в точке ис­пользуется символика: или если точка имеет координаты ,тo Отметим, что в определении не указывается закон стремления точки М к точке Л , поэтому он может быть любым. Функция 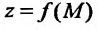называется бесконечно малой в точке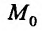 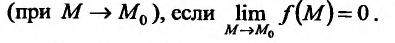Например, функция 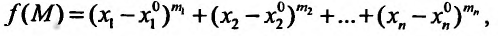где 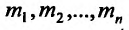- положительные числа, является бесконечно ма­лой в точке 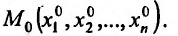Если функция 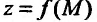имеет предел А в точке 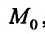, то ее можно представить в виде суммы предела и бесконечно малой функции в этой точк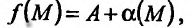е: где 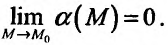Для функции 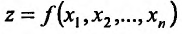можно определить понятие по­вторного предела, то есть предела по одной из переменных 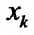при фиксированных значениях остальных переменных. Рассмотрим повторный предел для функции двух переменных 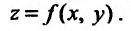Пусть функция 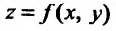задана в прямоугольной окрестност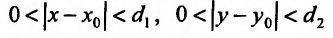и точки 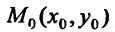и пусть для каждого фиксированного 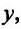удовлетворяющего условию 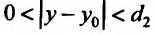существует предел функции 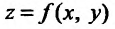одной пе­ ременной х в точке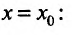

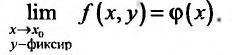Тогда, если существует предел А функции 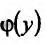в точке 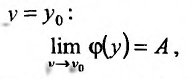то он называется 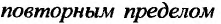для функции 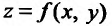в точке 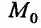, который обозначается следующим образом:

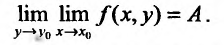Аналогично определяется повторный предел: 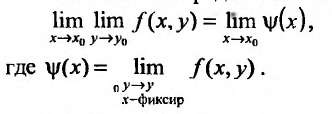Отметим, что если в точке 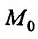функция 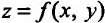имеет пре­ дел равный 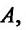и существуют пределы 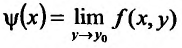и 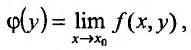то повторные пределы 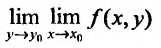и 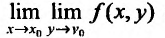существуют и оба равны А. Однако из существования повторных пределов еще не следует существования предела функции 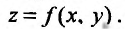Так, например, функ­ция 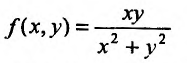не имеет предела в точке 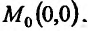хотя можно указать такие законы стремления точки 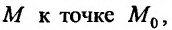, что повторные пределы будут равны: 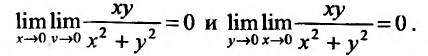Но если точка М стремится к точке 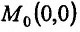по прямой 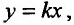, то значение повторного предела будет зависеть от значения 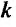, что и свидетельствует об отсутствии предела рассматриваемой функции в точке (О,О).

Может оказаться, что оба повторных предела существуют, но различны. Нетрудно заметать, что для функции 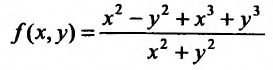будем иметь различные повторные пределы:

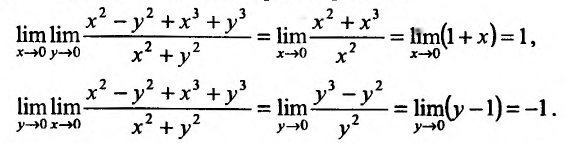
Поэтому, можно сделать вывод, что если для любого закона движения точки М к точке 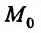повторные пределы существуют и они равны между собой, тогда и предел функции z = f(x, у) существует и равен этим повторным пределам.

Непрерывность функции двух переменных

Рассмотрим функцию п переменных 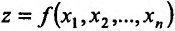, заданную на некотором множестве 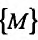пространства 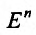. Пусть 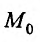-произвольная точка 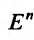, принадлежащая множеству 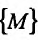и такая, что в любой 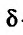-окрестности точки 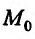содержатся точки множества .

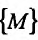Будем говорить, что функция z = f(М) непрерывна в точке 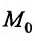, если предел этой функции в точке 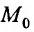существует и равен частному значению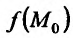. Символически непрерывность функции z = f(М) в точке 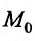можно записать в виде: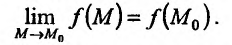

В частности, для функции двух переменных: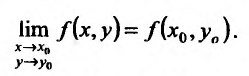

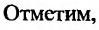что поскольку 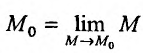, то условие непрерывности можно записать в виде:

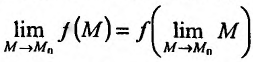
Значит, для непрерывной функции в точке 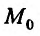символ lim предела и символ 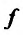характеристики функции можно менять местами.

Точки пространства 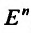, в которых функция z = f(м) не обладает свойством непрерывности, называются точками разрыва этой функции.

Используя определение предела функции 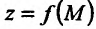в точке 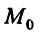по Коши, можно сформулировать определения непрерывности функции по Коши.

Если обозначить через 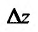полное приращение функции 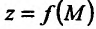, определяемое по формуле 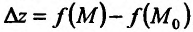, где М произвольная точка из области задания функции, то для непрерывности функции z = f(M) в точке 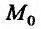необходимо и достаточно, чтобы ее приращение представляло в точке 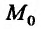бесконечно малую функцию, то есть

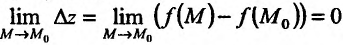
Аналогичным образом определяется непрерывность функции 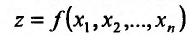по одной из переменных. Для этого вводятся частные приращения:

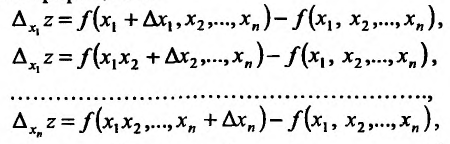
и тогда если 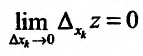, то функция 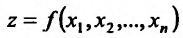называется непрерывной по переменной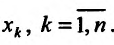

Очевидно, что из условия непрерывности функции 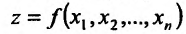в данной точке 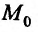вытекает непрерывность этой функции в точке 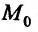по каждой из переменных 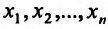. Однако, из непрерывности функции в точке 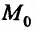по каждой из переменных 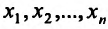не вытекает, вообще говоря, непрерывность функции в этой точке.

Для непрерывности функции n переменных справедливы многие аналогичные свойства непрерывных функций одной переменной: непрерывность сложной функции, устойчивость знака непрерывной функции, о прохождении через любое промежуточное значение, теоремы Вейрштраса и т.д.

Частные производные первого и высших порядков функции двух переменных

Пусть функция 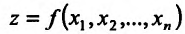n переменных задана на множестве {м} и точка 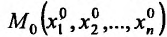- внутренняя точка данного множества. Зафиксируем все аргументы, кроме 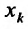, которому придадим произвольное приращение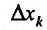, такое, чтобы точка с координатами 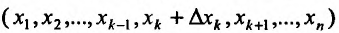находилась в области задания функции. Определим соответствующее частное приращение функции в точке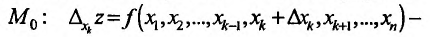

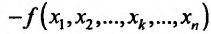. Составим отношение частного приращения 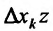к соответствующему приращению аргумента :

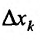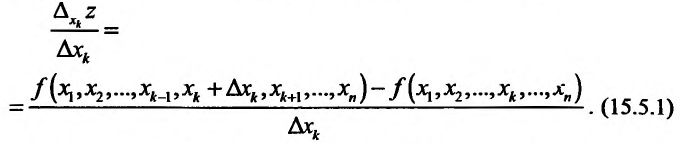
Отношение (15.5.1) представляет собой функцию 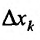, определенную для всех отличных от нуля значений 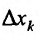, для которых точка 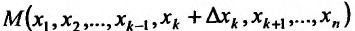принадлежит области задания функции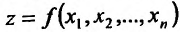

Определение 15.5.1. Если существует предел отношения (15.5.1) частного приращения 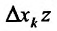функции к соответствующему приращению 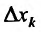аргумента 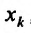, при стремлении 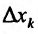к нулю, то тот предел называется частной производной функции 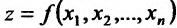в точке 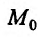по аргументу 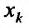и обозначается одним из символов:

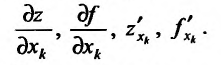
Таким образом,

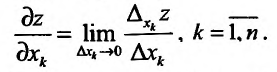(15.5.2)

В частности, для функции 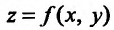двух переменных можно определить частные производные по х и у:

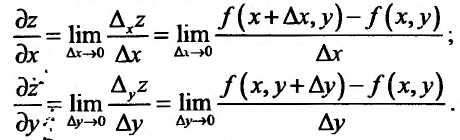
Из определения 15.5.1 следует, что частная производная функции 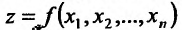по аргументу 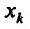представляет собой обыкновенную производную функции одной переменной 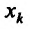при фиксированных значениях остальных переменных. Поэтому вычисление частных производных производится с использованием правил вычислений производных функций одной переменной и таблицы производных.

• Заказать решение задач по высшей математике

Пример:

Вычислить частные производные функций:

a)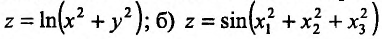

Решение:

Для вычисления частных производных воспользуемся правилами вычисления производных функции одной переменной, при этом, вычисляя частную производную по одной из переменных, другую считаем постоянной величиной.

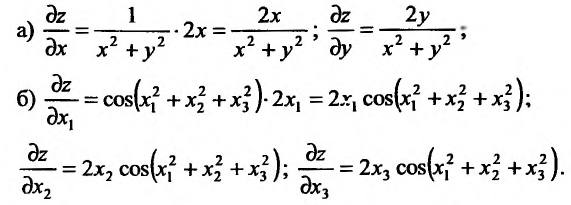
Предположим, что частная производная 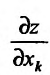по аргументу 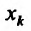функции 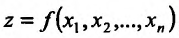, определенной на множестве 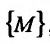, существует в каждой точке этого множества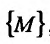. Тогда указанная частная производная представляет собой функцию n переменных, определенную на множестве {М}. Если эта функция 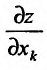имеет частную производную по аргументу 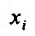в некоторой точке 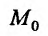множества {м), то она называется частной производной второго порядка функции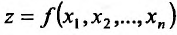в точке 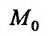сначала по аргументу хк, а затем по аргументу х, и обозначается одним из символов: 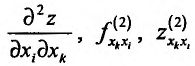. При этом, если 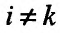, то частная производная 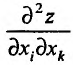называется смешанной частной производной второго порядка. После того как нами введено понятие второй частной производной, последовательно вводится понятие третьей частной производной, четвертой и т.д. Частную производную функции 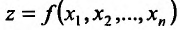П0 одному из аргументов в некоторой точке 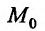от частной производной (n-l)-ro порядка по аргументам 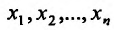(отдельные или даже все номера которых могут совпадать) называется частной производной n-го порядка функции 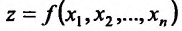в точке .

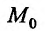В частности для функции 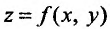двух переменных частные производные второго порядка определяются следующим образом.

Пусть частная производная 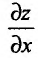по аргументу х функции z = f(х, у), определенной в области D. существует в каждой точке области D. В этом случае указанная частная производная представляет собой функцию двух переменных, также определенную в области D.

Тогда если эта функция 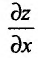имеет частную производную по аргументу х в некоторой точке 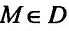, то указанную частную производную по х называют второй частной производной или частной производной второго порядка функции 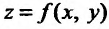в точке М по аргументу х и обозначают одним из символов: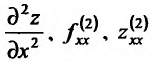

Аналогично определяется частная производная второго порядка по аргументу у.

Частная производная 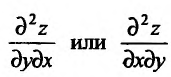называется смешанной производной второго порядка, т.е.

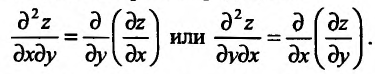
После того как введено понятие второй частной производной, можно последовательно ввести понятие третьей частной производной, затем четвертой и т.д.

Так как частная производная функции по аргументу х (у) определяется как обыкновенная производная функции одной переменной х (у)при фиксированном значении другой переменной, то методика вычисления частных производных высших порядков предполагает умение вычислять только обыкновенные производные первого порядка.

Пример:

Вычислить частные производные второго порядка функции

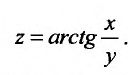
Решение:

Применив правило вычисления частных производных, получим: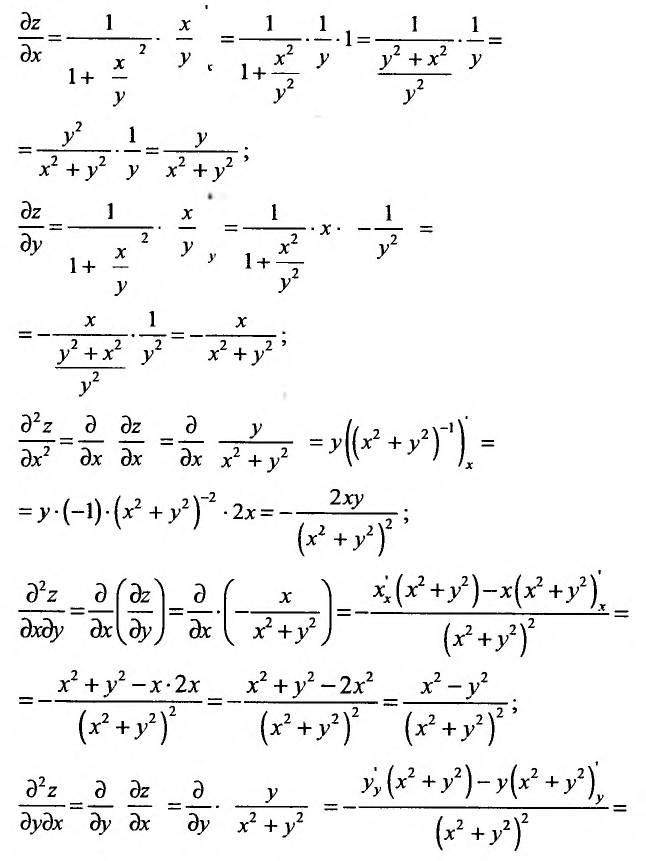

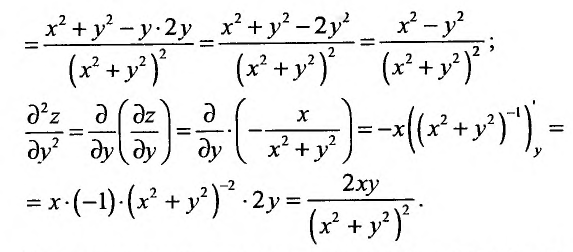
В рассмотренном примере смешанные частные производные 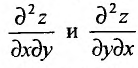равны друг другу. Вообще говоря, значения смешанных производных зависят от порядка, в котором производятся последовательные вычисления производных.

Достаточные условия независимости порядка вычисления производных определяются следующей теоремой.

Теорема 15.5.1. Пусть функция 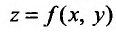в точке 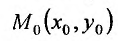имеет непрерывные частные производные второго порядка, тогда в этой точке частные производные 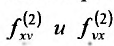равны.

Более того имеет место такая же теорема о независимости значений любой смешанной частной производной n-го порядка от порядка, в котором производятся вычисления частных производных.

Теорема 15.5.2. Пусть функция 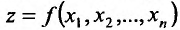имеет непрерывные частные производные n-го порядка в точке 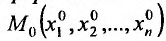Тогда в этой точке значение любой смешанной частной производной n-го порядка не зависит от порядка, в котором производится вычисление производных.